C++ 浮点数的存储与精度

C++ 浮点数的存储与精度

 

先看个例子（如下），我们看下int、float、double在内存的二进制表示

#include<stdio.h>
#include <stdlib.h>
#include <string.h>
#include<cstdlib>

bool isLittleEndian() {
    int x = 1;
    return *((char*) (&x)) == 1;
}

template<class T>
void printBinary(T d) {
    char* p = (char*)&d;
    int sz = sizeof(T); // bytes

    char* buff = new char[sz * 8 + 1];
    buff[sz * 8] = '\0';
    int used = 0;

    for (int n = 0; n < sz; n++) {
        for (int m = 0; m < 8; m++) {
            if ((p[n] >> m) & 1)
                used += sprintf(buff + used, "1");
            else
                used += sprintf(buff + used, "0");
        }
    }

    if (isLittleEndian()) {
        int a = 0;
        int b = sz * 8 - 1;
        while (a < b) {
            buff[a] ^= buff[b];
            buff[b] ^= buff[a];
            buff[a] ^= buff[b];
            a++;
            b--;
        }
    }

    printf("%s\n", buff);
    delete [] buff;
}

int main() {
    int i = 121;
    int i2 = -4;
    float f = 98.1;
    double d = 98.1;

    printBinary(i);     // 00000000000000000000000001111001
    printBinary(i2);    // 11111111111111111111111111111100
    printBinary(f);     // 01000010110001000011001100110011
    printBinary(d);     // 0100000001011000100001100110011001100110011001100110011001100110
}

对int类型，其内存存储的是二进制补码，比较好理解，对float和double类型而言，其二进制表示怎么理解呢？

 

C/C++采用的是IEEE浮点标准，它以“二进制的科学表示法”表示一个小数：

 

 

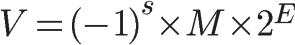
其中：

• (-1)^s 表示符号位，当s=0，V为正数；当s=1，V为负数；
• M 表示有效数字，1 <= M < 2；
• 2^E 表示指数位。

举例来说，十进制的5.0，写成二进制是101.0，相当于1.01×2^2。那么，按照上面V的格式，可以得出s=0，M=1.01，E=2。

十进制的-5.0，写成二进制是-101.0，相当于-1.01×2^2。那么，s=1，M=1.01，E=2。

 

关于 M

注意，由于1≤M<2，也就是说，M可以写成1.xxxxxx的形式，其中xxxxxx表示小数部分。IEEE 754规定，在保存M时，默认这个数的第一位总是1，因此可以被舍去，只保存后面的xxxxxx部分。比如保存1.01的时候，只保存01，等到读取的时候，再把第一位的1加上去。这样做的目的，是节省1位有效数字。以32位浮点数为例，留给M只有23位，将第一位的1舍去以后，等于可以保存24位有效数字。

 

关于 E

首先，E为一个无符号整数（unsigned int），如果E为8位，它的取值范围为0~255；如果E为11位，它的取值范围为0~2047。

其次，科学计数法中的E是可以出现负数的，所以IEEE 754规定，E的真实值必须再减去一个中间数，对于8位的E，这个中间数是127；对于11位的E，这个中间数是1023。

比如，2^10的E是10，所以保存成32位浮点数时，必须保存成10+127=137，即10001001。

最后，指数E可以再分成三种情况：

1. E不全为0或不全为1。这时，浮点数就采用上面的规则表示，即指数E的计算值减去127（或1023），得到真实值，再将有效数字M前加上第一位的1。
2. E全为0。这时，浮点数的指数E等于1-127（或者1-1023），有效数字M不再加上第一位的1，而是还原为0.xxxxxx的小数。这样做是为了表示±0，以及接近于0的很小的数字。
3. E全为1。这时，如果有效数字M全为0，表示±无穷大（正负取决于符号位s）；如果有效数字M不全为0，表示这个数不是一个数（NaN）。

 

 

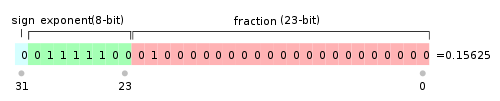
以float为例，最高的1位是符号位s，接着的8位是指数E，剩下的23位为有效数字M。

如下图，E=01111100，对应的十进制为124，124再减去中间数127，结果为-3；

M=01000...，对应的十进制为2^-2=0.25，还需要加上1，结果为1.25；

该浮点数结果 (-1)⁰ * 1.25 * 2^-3 = 0.15625。

 

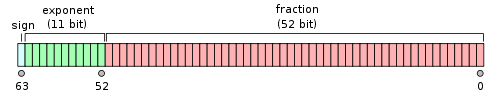
以double为例，最高的1位是符号位S，接着的11位是指数E，剩下的52位为有效数字M。

 

 

总结如下：

	字节数	符号位	指数位	尾数位
float	4 bytes	1 bit	8 bit	23 bit
double	8 bytes	1 bit	11 bit	52 bit

范围：

float的指数范围为-127 ~ 128，double的范围是-1023 ~ 1024。

负指数决定了绝对值最小的非零数，正指数决定了绝对值最大的数。也即决定了范围。

也即float的范围为 -2^{128 ~} 2¹²⁸，double的范围是 -2^{1024 ~} 2¹⁰²⁴。

精度：

float和double的精度是由尾数位决定的。浮点数在内存中是按照科学计数法来存储的，其整数部分始终是一个隐藏着的1。由于他是不变的，因此对精度不会造成影响的。

float精度范围是：能达到23二进制位，约为 23 * log₁₀2 = 6.92 个十进制位；

double的精度范围是：能达到23二进制位，约为 52 * log₁₀2 = 15.65 个十进制位；

OK，最后我们再回到开头的例子，

float f = 98.1;  // 01000010110001000011001100110011

看下其二进制，最高位符号位0，中间指数位 10000101 的十进制位133，E=133-127=6；

尾数位 10001000011001100110011，对应的十进制=0.532812，M=1.532812；

最后计算结果 1.532812 * 2⁶ = 98.099998，精度为6位！

这里我写了个简单函数用来解析float的二进制：

float parseFloat(char* s) {
    int sign = s[0] - '0';
    float M = 0;
    int E = 0;

    for (int n = 1; n <= 8; n++) {
        E = E * 2 + (s[n] - '0');
    }

    for (int n = 9; n <= 31; n++) {
        M += pow(2, 8 - n) * (s[n] - '0');
    }

    printf("sign=%d, E=%d, M=%f\n", sign, E, M);

    return pow((-1), sign) * (M + 1) * pow(2, (E - 127));
}

int main() {
  
    float f = 98.1;
  
    printBinary(f);     // 01000010110001000011001100110011
    
    printf("float = %f\n", parseFloat("01000010110001000011001100110011"));
  
}