布隆过滤器概念和原理
概念
布隆过滤器, bloom filter 是一种时间、空间效率很高的随机数据结构, 它利用位数组很简洁地表示一个集合, 并能判断一个元素是否属于这个集合。由于hash函数难免会产生冲突, 布隆过滤器会存在低概率的误判(不存在的元素误判为存在集合), 但它绝不会存在漏判，已经在集合中的元素经过多个hash函数hash值后一定会在集合中能匹配到。
布隆过滤的核心思想
bloom filter 的核心思想是通过多个不同的hash函数来解决冲突。
搭建布隆过滤器的一般流程
1、构建m位数组
初始化m比特的数组, 来保存信息。初始值每一位置0
2、构建k个hash函数
如下图所示, 将x1和x2元素添加到布隆过滤器。首先通过k个hash函数hash得到k个hash值, 然后再将位整数组中对应的比特位置1，这样就把元素映射到位阵数组中了。
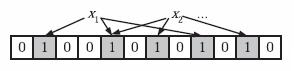
3、判断元素是否在布隆过滤器中
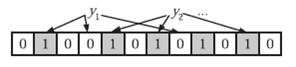
假设我们要判断元素y1和y2是否在布隆过滤中, 只需要对元素y1、y2用k个hash函数得到k个hash值，再和位阵数组对应的比特位进行匹配, 如果对应的k个位置都被置1, 则y1存在布隆过滤中；反之亦然。
布隆过滤的优缺点
- 优点
小存储空间，容纳大量元素。上面提到的m位位阵数组，每个位要么是0要么是1.掐指一算，有2m种组合。事实上，我们知道m位位阵数组可容纳的元素个数可能会不止2m， hash存在冲突，k个hash函数冲突的概率几乎可不计。
- 缺点
可能存在误判，不存在的元素会因为hash冲突导致误判存在位阵数组中；hash函数的选型会影响算法的效果，选型显得尤为关键。另外，在位阵数组中，同个位子的1可能对应多个元素，导致删除的时候不能简单把它置0，删除的维护代价太高了。
幸好误判率是可控的，假设kn<m且各个哈希函数是完全随机的。当集合S={x1, x2,…,xn}的所有元素都被k个哈希函数映射到m位的位数组中时，误判率的计算公式是：
(1 – e^(-k * n / m)) ^ k 对应的java代码：Math.pow((1 – Math.exp(-k * numberOfElements / (double) bitSetSize)), k);
布隆过滤的应用场景
布隆过滤器存在低概率的误判情况, 它更适合用于允许容错（错误率不影响业务）、需要节省存储空间、追求时间高效率的场景。如 过滤垃圾邮件等
布隆过滤器与redis结合使用
