数据结构：循环队列

1.写在前面

　　附我的另一篇博客：C_队列的链式表示和描述

数组表示的问题　

　　　　对于队列最好的方法是使用链表实现，因为对于数组来说，队列可能会出现下面这种情况：

　　　　

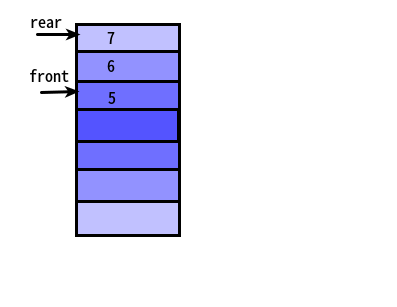
　　　　如图所示，不可以继续添加元素，否则会造成数组越界而遭致程序出错。然而此时又不应该扩充数组，因为还有大量实际空间未被占用。

　　　　此时我们应该如何解决这个问题呢？我们将其实现为循环队列。

理解循环队列

　　　　何谓循环队列？首先我们要说明的是循环队列仍然是基于数组实现的。但是为了形象化的说明问题，我们如下图所示

　　　　　　　　　　

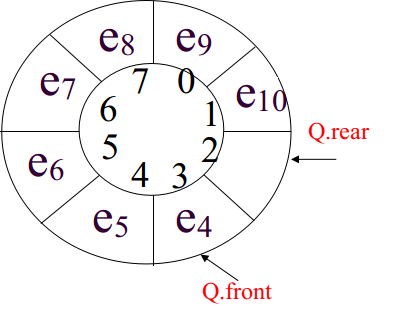
　　　　1.图中有两个指针(其实就是两个整数型变量，因为在这里有指示作用，所以这里理解为指针)front、rear,一个指示队头，一个指示队尾。

　　　　2.rear和front互相追赶着，这个追赶过程就是队列添加和删除的过程，如果rear追到head说明队列满了，如果front追到rear说明队列为空。

　　说明：

　　　　令队列空间中的一个单元闲置，使得队列非空时，Q.rear与Q.front之间至少间隔一个空闲单。

　　　　3.我们把它掰弯，用的是求余，这样两个值就不会跑出最大范围，并且可以实现弯曲的效果，所以说对于循环队列我们必须给定最大值MAXQSIZE。

　　　　   这其实是我们臆想的，反正我们要做的就是利用循环来解决空间浪费的问题。　　

循环队列的实现过程

　　　　☆当添加一个元素时,(rear+1)%MAXQSIZE; //理解为什么求余？

　　　　☆当删除一个元素时,(front+1)%MAXQSIZE；//理解为什么求余？

　　　　☆当rear=front的时候，队列可能是满，也可能是空。

　　　　　　因为存在满和空两种情况，我们需要分别判断：

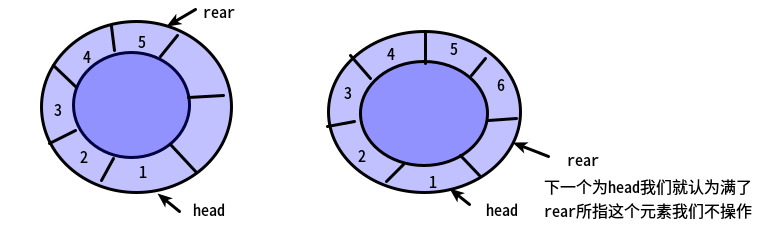
　　　　　　　　☆满：当队列添加元素到rear的下一个元素是head的时候，也就是转圈子要碰头了，我们就认为队列满了。(Q.rear+1)%MAXSIZE=Q.front

　　　　　　　　☆空：当队列删除元素到head=rear的时候，我们认为队列空了。Q.rear==Q.front,不一定为0

　　图示：

　　　　

队列操作的一些说明

队列长度：Q.rear-Q.front；

队头元素：Q.base[Q.front]；

队尾元素：Q.base[Q.rear-1]；

 

2.代码分解

2.1添加操作

　　　元素入队时仅修改队尾指针rear —— ++.

status EnQueue(SqQueue *q,QElemtype e)
{
    //插入到队尾
    if((q->rear+1)%MAXQSIZE==q->front)
        return 0;
    q->base[q->rear]=e;
    q->rear=(q->rear+1)%MAXQSIZE;
    return 1;
}

 

2.2删除操作

　　  元素出队列时只修改队头指针front——++.

status DeQueue(SqQueue *q)
{
    if(q->front==q->rear)
        return 0;
    printf("%d",q->base[q->front]);
    q->front =(q->front+1)%MAXQSIZE;
    return 1;
}

2.3获取队列长度

int QueueLength(SqQueue *q)
{
    return (q->rear-q->front+MAXQSIZE)%MAXQSIZE;
}

2.4对节点的定义

#define MAXQSIZE 100
typedef int QElemtype;
typedef int status;

typedef struct{
    QElemtype *base;
    int front;
    int rear;
    }SqQueue;

2.5测试方法

void main()
{
    SqQueue *q;
    q=(SqQueue*)malloc(sizeof(SqQueue));
    q=InitQueue(q);
    EnQueue(q,5);
    EnQueue(q,4);
    EnQueue(q,3);
    EnQueue(q,2);
    EnQueue(q,1);
    printf("队列长度为：%d\n",QueueLength(q));
    DeQueue(q);
    DeQueue(q);
    DeQueue(q);
    DeQueue(q);
    DeQueue(q);
}

 2.6初始化队列

SqQueue* InitQueue()
{
    SqQueue *q;
    q=new SqQueue;
    q->base=new int[MAXQSIZE];
    q->rear=q->front=0;
    return q;
}