ICP与NDT之精度篇

ICP问题

匹配未考虑形状，会陷入局部最小值，受形状影响大，鲁棒性不够好。换言之精度会失效。

马氏距离引入

将点云和位姿矩阵看做概率量（随机变量），引入马氏距离评定（ICP为欧式距离评定），由于协方差矩阵可以度量多个维度上的信息（公式0-1、公式0-2、公式0-3），故可以刻画多维信息，从理论上我们就可以消除ICP无形状考虑的问题（鲁棒性不够好、精度失效）
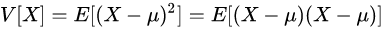（公式0-1） 一维只有方差
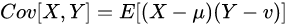.（公式0-2） 二维协方差
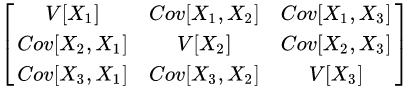（公式0-3） 三维协方差矩阵

NDT改善

通过某区域内（划分网格内）概率分布可以得到点云的形状分布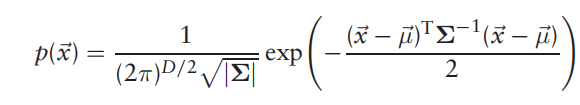， （公式1）
上述公式可以看做归一化的马氏距离，质心和协方差可以表示出各点和点云中心位置与各点云方向（得益于协方差），故可以表示点云位置形状等丰富信息。（另外注意到上述对马氏距离取了负，故越远越接近0，越近越接近1）

上图为通过概率刻画点云，左边为隧道原始点云，右边为每个方块内点的概率（公式1）表示越接近1的颜色越浅，以上得益于马氏距离的信息丰富性，可以看出拟合后形状是比较相近的（这是一个很大的进步）。

上图为一维、二维、三维的概率（马氏距离）表示。
一维中横坐标为一维x位置，纵坐标为概率值（马氏距离），值越大（马氏距离越小）越接近中心，概率代数值越接近1，拍到一维直线上，用颜色表示大小构成二维信息，颜色越浅越接近一；
二维中有两个方向的度量，同样横纵坐标为二维xy位置颜色表示概率值，也就是说概率是复合结果，二维马氏距离展开会有x与y的相关项，cov（x，y）也刻画了另一维影响
特别的：当其中一维很接近这一维的质心时时会退化成一维形式（如：考虑y=v则+的右项=0，且cov（x,y）=0），也就是说离哪一维更近哪一维就起主要作用。
三维中有三个方向的度量，为了表示三维加入坐标轴，坐标轴压缩量表示了点云分布的大致形状。特别的：其中一维接近这一维的质心时会退化为二维，两维接近时会退化成一维。
注：加入退化情况说明是为了方便理解协方差所起作用

从以上可以看出表面方向和光滑度可以从协方差矩阵的特征向量值和特征值来评估。
我们求以下最优问题即可

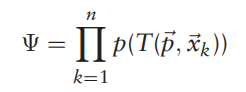
上图的意思也就是，通过给定位姿p将点云x下标第k个通过T函数之后，求相应的概率值。
我是分割线---------------------------------------------------------------------------------------------------我是分割线

以下是构建方程技巧trick部分，可以跳过
首先是求优化问题argmin的通用求法，取负

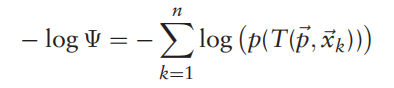
然后对于较远点云的影响（近0值），乘以一系数c1以减小其影响也就是增大exp（），我们预估较远点比例为55%然后c1=10*（1-55%） c2=比例/选取点云体积

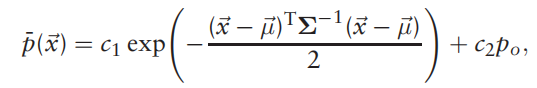
注：较远点的影响是分割网格大小的关键，对于较大的网格，较远点影响会加剧

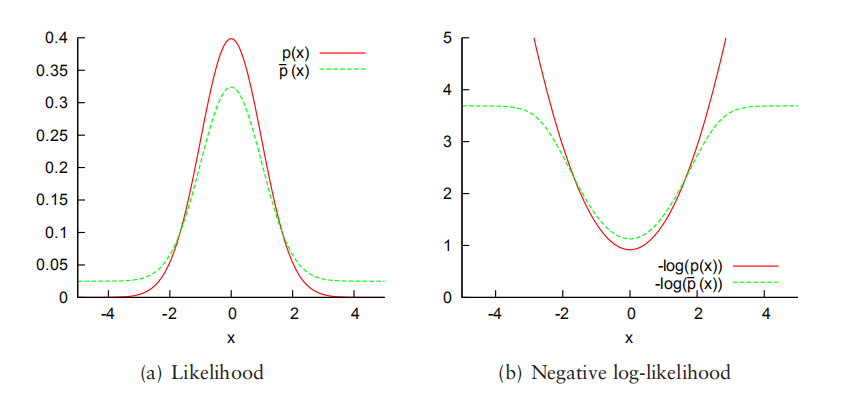
上图中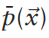是取系数之后的概率值，可以看到在一维情况下消除了无穷大值（较远点概率值取负log值）的影响
然后进行高斯拟合，也就是
将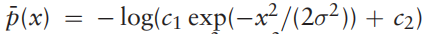变为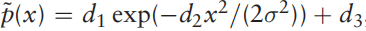
将d1、d2、d3摘出来

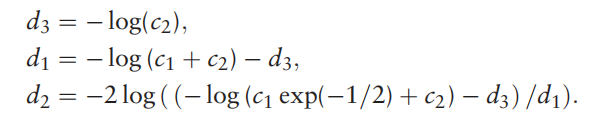
其中有三个未知量，我们取三个特殊值值即可解这个三元一次方程，分别是x=0、x=σ、x=∞
以上可以大大减小我们的计算量，快速得到d1、d2、d3
得益于高斯近似，现在我们的优化方程变为

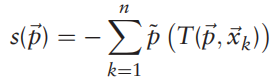
对于等式右边的记号我们从新记一个，叫做得分记为s，接下来最优化s求解位姿p就行了

我是分割线---------------------------------------------------------------------------------------------------我是分割线

谈完了方程构建，接下来到了求解部分，依旧是trick部分，可以跳过
首先我们求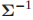但是三个点构成一个平面，这样就确实了一维的特征值，变成奇异矩阵不满秩，所以我们只对大于5个点的网格进行计算。
另外对于特殊情况、降维问题，若最大的特征值比最小的大100倍，我们认为降维了，将最小特征向量的尺度变为最大特征值/100，这种倍数关系可以优化计算。

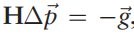
求解高斯牛顿法二阶，专门写了一篇高斯牛顿相关的文章，如果有不懂的可以点击这里：this。
其中梯度（雅克比矩阵/一阶导数矩阵）矩阵为

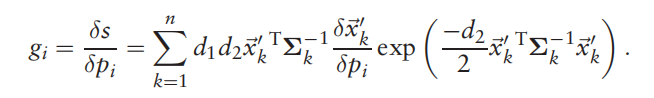
海塞矩阵（二阶导数矩阵）
为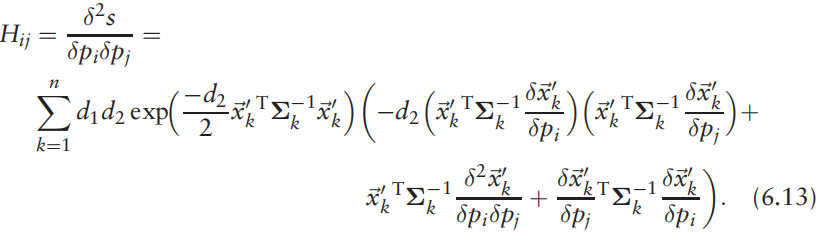
梯度详细（雅克比矩阵/一阶导数矩阵）：


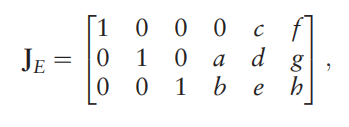
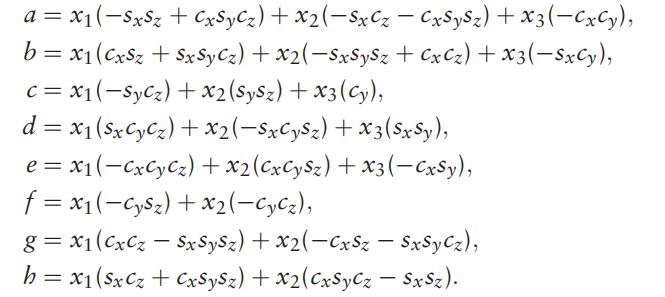
黑塞详细（二阶导数矩阵）：

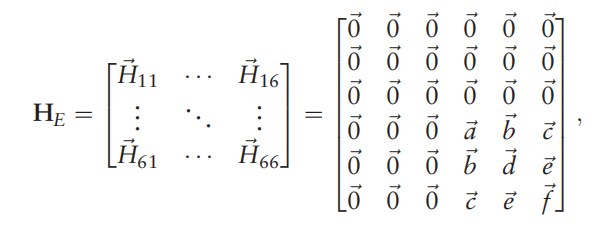
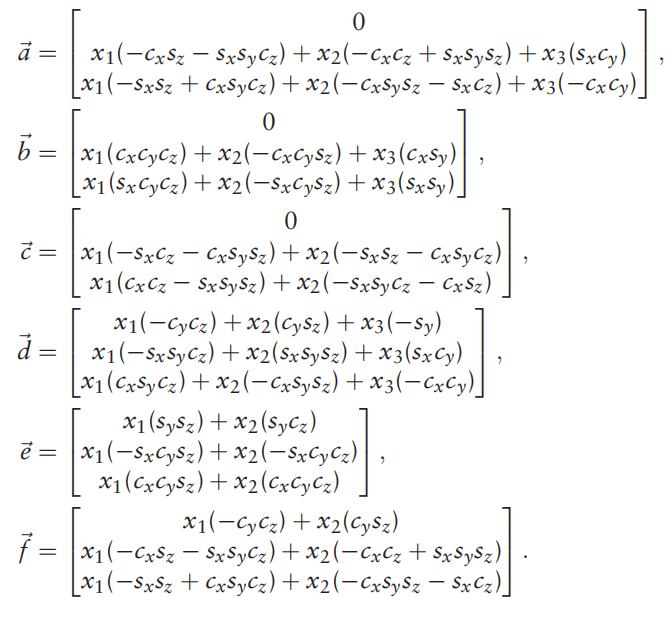
我是分割线---------------------------------------------------------------------------------------------------我是分割线

以上终于讲完了原理部分：
最终我们整理一遍具体算法流程：
首先对范围内的三维点云进行三维网格（1m³为例）划分，也就是进行下采样，下采样之后会记录网格内的协方差（形状）
搜索目标点云的最近邻网格（下采样后的）
根据搜索到的点的网格参数计算与马氏距离相关的高斯概率总和，迭代优化马氏距离求解旋转平移矩阵，直到马氏距离最小（形状最相近）的即是所找到的位姿矩阵。

我是分割线---------------------------------------------------------------------------------------------------我是分割线

精度方面ICP匹配对平移/各点云相对偏移鲁棒性更好，NDT对旋转/形状鲁棒性更好，精度也更高。下一篇谈论时间（ICP耗时很短、NDT耗时比较长）