Windows GDI Rotation（官网解析）

许多CAD应用程序提供在客户区域绘制旋转对象的功能。包含旋转功能的应用程序使用SetWorldTransform函数来设置适当的world-space到page-space的转换。这个函数接收一个指向包含了适当值的XFORM结构体的指针。XFORM的eM11、eM12、eM21和eM22成员分别指定了旋转角度的余弦、正弦、负正弦和负余弦。当旋转发生时，构成对象的点相对于坐标空间原点旋转。下图显示的是当从世界坐标空间复制到页面坐标空间时旋转了30度的一个20x20单位的矩形。

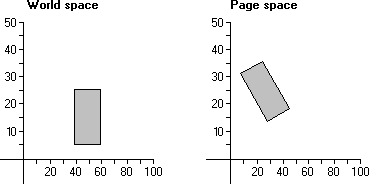
在上图中，矩形中的每个点都相对于坐标空间的原点旋转了30度。

下面的算法是为相对于坐标系原点旋转了角度A的点（x,y）计算新的坐标x'

x' = (x * cos A) - (y * sin A)

下面的算法是为相对于坐标系原点旋转了角度A的点（x,y）计算新的坐标y'

y' = (x * sin A) + (y * cos A)

这两种旋转变换可以组合成一个2x2矩阵，如下所示：

|x' y'| == |x y| * | cos A   sin A| 
                   |-sin A   cos A|

产生旋转的2x2矩阵包含以下值：

| cos30    sin30| 
|-sin30    cos30|

| .8660    .5000| 
|-.5000    .8660|

 旋转算法公式推导

旋转算法基于三角函数的加法定理，即两个角度（A1和A2）之和的三角函数可以分别用这两个角度的三角函数来进行表达，具体如下：

sin(A1 + A2) = (sin A1 * cos A2) + (cos A1 * sin A2) 
cos(A1 + A2) = (cos A1 * cos A2) - (sin A1 * sin A2)

下图显示点P逆时针旋转至新的点P‘。此外，它显示了两个三角形，这两个三角形是由坐标空间原点至每个点绘制的一条线和从每个点通过X轴线绘制的一条线所组成。见下图

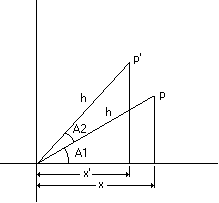
用三角函数，点p的x坐标可以通过将斜边h的长度乘以A1的余弦得到。如下

x = h * cos A1

点p的y坐标可以通过将斜边h的长度乘以A1的正弦得到，如下

y = h * sin A1

同样的原理，点p '的x坐标可以通过将斜边h’的长度乘以(A1 +A2)的余弦得到，如下

x' = h‘ * cos (A1 + A2)

最后，点p '的y坐标可以通过将斜边h’的长度乘以(A1 +A2)的正弦得到，如下

y' = h‘ * sin (A1 + A2)

使用加法定理，前面的算法可以变成如下：

x' = (h * cos A1 * cos A2) - (h * sin A1 * sin A2) 
y' = (h * cos A1 * sin A2) + (h * sin A1 * cos A2)

对于旋转了角度A2的给定点的旋转算法可以通过用x代替每次出现的(h * cos A1)和用y代替每次出现的(h * sin A1)来获得，如下

x' = (x * cos A2) - (y * sin A2) 
y' = (x * sin A2) + (y * cos A2)

转换为矩阵表达：

|x' y'| == |x y| * | cos A2   sin A2| 
                   |-sin A2   cos A2|