Matrix Transformation of Images in C#, using .NET GDI+ / GDI+ / C#

前言

.NET中2D图形变换已经被System.Drawing.Drawing2D命名空间的Matrix类大大简化了。在这篇文章中，我想和读者朋友分享一下Matrix类应用于2D图形变换的使用方法。

背景

Matrix类采用3行2列共计6个元素的排列组合；比如，默认构造函数构造的默认矩阵的值为（1，0，0，1，0-，0）；在矩阵中表示为：

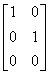
以上矩阵是简化版本：

最后一列始终保持：

因此，x轴上移动3和y轴上移动2的平移变换将表示为：

但是在内部表示为

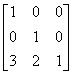
需要注意的重要一点是变换矩阵与图形向量相乘；比如说，我们有带四个点位的图片：(1,1) ( 2,3) (5,0) (6 7)。这个图片向量会表示为4行2列的矩阵：

在内部则表示为

当变换矩阵对图形矩阵进行运算时，变换矩阵在图形矩阵的右边进行相乘；

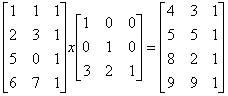
所得结果的矩阵中的最后一列可以忽略。因此计算结果后的图片会有(4,3) (5,5) (8,2) and (9,9)。

复合变换由两个或多个矩阵的乘积组成。比如，x轴上的因子为2，y轴上的因子为3的缩放矩阵。

在内部表示为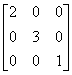

当我们对先平移再缩放进行复合变换时，缩放矩阵会位于平移矩阵的右侧进行相乘：

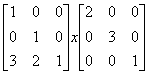
同样的，如果我们对先缩放再平移进行复合变换时，平移矩阵会位于缩放矩阵的右侧进行相乘。

向右相乘则称为appending，对于左乘则为prepending，左边的矩阵总是先进行计算。