Text Transformation in GDI+（一）

ScaleTransform, RotateTransform, 和 TranslateTransform函数是用于变换文本形式的。我们也可以使用转换矩阵来变换文本。

我们使用转换属性创建一个矩阵对象，并使用Graphics对象的转换属性将其应用到表面。清单10.21创建了一个矩阵对象，并将其设置为Transform属性。然后我们调用DrawString，它在Form上绘制文本。

 

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Drawing;
using System.Windows.Forms;
using System.Drawing.Drawing2D;


namespace TextTransformationDemo
{
    class TextTransformationDemo:Form
    {
        static void Main(string[] args)
        {
            Application.Run(new TextTransformationDemo());
        }
        public TextTransformationDemo()
        {
            Text = "文字变换测试";
        }
        protected override void OnPaint(PaintEventArgs e)
        {
            Graphics g = e.Graphics;
            string str =
                " colors ,font s and text are common" +
                "elements of grahpics programming." +
                "int thw arcile ,you learned" +
                "about the colosr ,fonts and text" +
                "representations in the" +
                ".net framework class lobrary" +
                "you learned how to create" +
                "these elements and use them in GDi.";
            //创建Matrix对象
            Matrix M = new Matrix(1,0,0,1,100,100); //此为平移矩阵
            //g.RotateTransform(45.0f,MatrixOrder.Prepend);

            //g.TranslateTransform(30, 30);
            g.Transform = M;
            g.DrawString(str,
                new Font("Verdana",10),
                new SolidBrush(Color.Blue),
                new Rectangle(0,0,200,300));
        }
    }
}

 

 

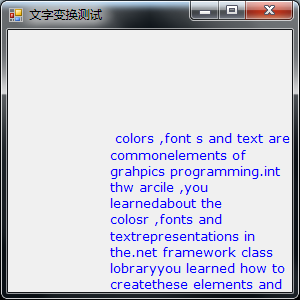
 下面将代码第36行和第38行解封，如下：

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Drawing;
using System.Windows.Forms;
using System.Drawing.Drawing2D;


namespace TextTransformationDemo
{
    class TextTransformationDemo:Form
    {
        static void Main(string[] args)
        {
            Application.Run(new TextTransformationDemo());
        }
        public TextTransformationDemo()
        {
            Text = "文字变换测试";
        }
        protected override void OnPaint(PaintEventArgs e)
        {
            Graphics g = e.Graphics;
            string str =
                " colors ,font s and text are common" +
                "elements of grahpics programming." +
                "int thw arcile ,you learned" +
                "about the colosr ,fonts and text" +
                "representations in the" +
                ".net framework class lobrary" +
                "you learned how to create" +
                "these elements and use them in GDi.";
            //创建Matrix对象
            Matrix M = new Matrix(1,0,0,1,100,100); //此为平移矩阵
            g.RotateTransform(45.0f,MatrixOrder.Prepend);

            g.TranslateTransform(30, 30);
            g.Transform = M;
            g.DrawString(str,
                new Font("Verdana",10),
                new SolidBrush(Color.Blue),
                new Rectangle(0,0,200,300));
        }
    }
}

 

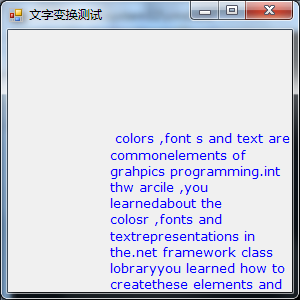
 综合上述两个Demo可见，g.RotateTransform(45.0f,MatrixOrder.Prepend);和g.TranslateTransform(30, 30);没有起到旋转和平移的作用，全部由Matrix M = new Matrix(1,0,0,1,100,100);在主导控制。

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Drawing;
using System.Windows.Forms;
using System.Drawing.Drawing2D;


namespace TextTransformationDemo
{
    class TextTransformationDemo:Form
    {
        static void Main(string[] args)
        {
            Application.Run(new TextTransformationDemo());
        }
        public TextTransformationDemo()
        {
            Text = "文字变换测试";
        }
        protected override void OnPaint(PaintEventArgs e)
        {
            Graphics g = e.Graphics;
            string str =
                " colors ,font s and text are common" +
                "elements of grahpics programming." +
                "int thw arcile ,you learned" +
                "about the colosr ,fonts and text" +
                "representations in the" +
                ".net framework class lobrary" +
                "you learned how to create" +
                "these elements and use them in GDi.";
            //创建Matrix对象
            Matrix M = new Matrix(1,0,0.5f,1,0,0); //此为平移矩阵
            g.RotateTransform(45.0f,MatrixOrder.Prepend);

            g.TranslateTransform(-20, -70);
            g.Transform = M;
            g.DrawString(str,
                new Font("Verdana",10),
                new SolidBrush(Color.Blue),
                new Rectangle(50,20,200,300));
        }
    }
}

 

 我们可以通过改变矩阵的值来应用剪切和其他效果。比如，我们改变矩阵如下：

Matrix M = new Matrix(1, 0.5f, 0, 1, 0, 0);

新的代码会产生如下效果

 

 

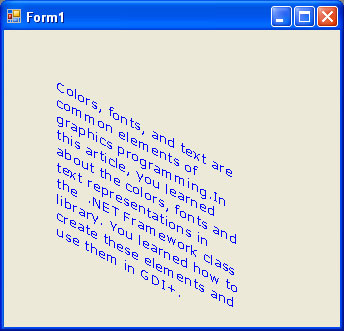
 我们可以通过改变矩阵对象的值来反转文本，如下所示

 

 

 

 变换顺序的重要性

矩阵对象可以存储单个转换或一系列转换。一系列转换称为复合转换，它是各个转换的矩阵相乘的结果。

在复合转换中，单个转换的顺序非常重要。矩阵运算不是累积的。比如Graphics -> Rotate -> Translate -> Scale -> Graphics的运算结果不同于Graphics -> Scale -> Rotate -> Translate -> Graphics的运算结果。执行顺序很重要的原因是类似旋转和缩放的变换是相对于坐标系统的原点来执行响应。对象以原点为中心进行缩放的结果，与对象远离原点进行缩放的结果，是不相同的。类似地，对象以原点为中心进行旋转的结果，与对象远离原点进行旋转的结果，是不相同的。

MatrixOrder枚举是transformation函数的一个参数，表示转换顺序；它有两个值： Append and Prepend.

让我们写个程序来看一下transformation order 是如何工作的。

在应用Scale -> Rotate -> Translate变换系列之前和之后来看一下绘制矩形的变化。

 Scale -> Rotate -> Translate transformation order

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Drawing;
using System.Windows.Forms;

namespace MatrixOrderDemo
{
    class MatrixOrderDemo:Form
    {
        static void Main(string[] args)
        {
            Application.Run(new MatrixOrderDemo());
        }
        public MatrixOrderDemo()
        {
            Text = "转换顺序测试";
        }
        protected override void OnPaint(PaintEventArgs e)
        {
            Graphics g = CreateGraphics();
            g.Clear(this.BackColor);

            Rectangle rect =
                new Rectangle(20,20,100,100);
            Brush brush = new SolidBrush(Color.Red);

            //此为绘制方格网
            for (int i = 0; i < ClientSize.Width; i +=10)
            {
                for (int j = 0; j < ClientSize.Height; j +=10)
                {
                    g.DrawLine(new Pen(Color.Gray),new Point(i,0),new Point(i,ClientSize.Height));
                    g.DrawLine(new Pen(Color.Gray),new Point(0,j),new Point(ClientSize.Width,j));
                }
            }

            g.FillRectangle(brush,rect);

            g.ScaleTransform(1.5f,0.5f);
            //g.RotateTransform(45.0f,System.Drawing.Drawing2D.MatrixOrder.Append);
            //g.TranslateTransform(150.0f,50.0f,System.Drawing.Drawing2D.MatrixOrder.Append);
            g.FillRectangle(brush,rect);

            //此为验证的矩形
            Rectangle rect1 =
                new Rectangle(20, 20, 100, 100);
            g.FillRectangle(new SolidBrush(Color.Green), rect1);

            brush.Dispose();
            g.Dispose();
        }
    }
}

 

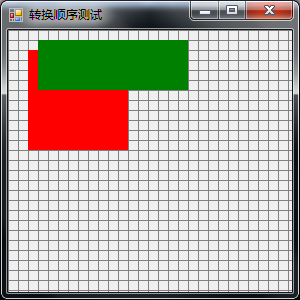
g.ScaleTransform(1.5f,0.5f);运行之后，整个世界坐标系会将横轴扩大1.5倍，纵横缩小0.5倍；这样的后果是，用于验证的红色矩形原坐标与长宽为new Rectangle(20, 20, 100, 100);在ScaleTransform运行后，实绘制出来如上图所示，即坐标与长宽会分别在横轴扩大1.5倍，在纵横缩小0.5倍，为new Rectangle(20*1.5=30,20*0.5=10,100*1.5=150,100*0.5=50);(30,10,150,50)与上图中绿色矩形的坐标与长度的结果是可以对应上的。

2022年7月23日更新：

上述红色矩形的四个坐标点为（20，20）（120，20）（20，120）（120，120），转化为内部矩阵为

 

ScaleTransform(1.5f,0.5f)的矩阵表达式为

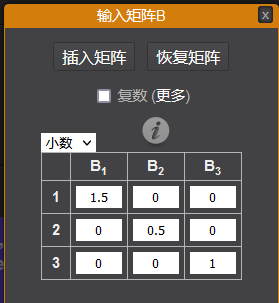
两个矩阵相乘的结果是

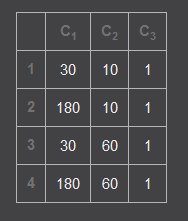
将上述矩阵结果转化为坐标点为（30，10）（180，10）（30，60）（180，60）

可以看到，此四个坐标点与红色矩形的坐标是可以对应上的！

 

 

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Drawing;
using System.Windows.Forms;

namespace MatrixOrderDemo
{
    class MatrixOrderDemo:Form
    {
        static void Main(string[] args)
        {
            Application.Run(new MatrixOrderDemo());
        }
        public MatrixOrderDemo()
        {
            Text = "转换顺序测试";
        }
        protected override void OnPaint(PaintEventArgs e)
        {
            Graphics g = CreateGraphics();
            g.Clear(this.BackColor);

            Rectangle rect =
                new Rectangle(20,20,100,100);
            Brush brush = new SolidBrush(Color.Red);

            //此为绘制方格网
            for (int i = 0; i < ClientSize.Width; i +=10)
            {
                for (int j = 0; j < ClientSize.Height; j +=10)
                {
                    g.DrawLine(new Pen(Color.Gray),new Point(i,0),new Point(i,ClientSize.Height));
                    g.DrawLine(new Pen(Color.Gray),new Point(0,j),new Point(ClientSize.Width,j));
                }
            }
            g.DrawLine(new Pen(Color.Green),new PointF(14.14f,0),new PointF(14.14f,28.28f));
            g.DrawLine(new Pen(Color.Green),new PointF(0,28.28f),new PointF(14.14f,28.28f));

            g.FillRectangle(brush,rect);

            g.ScaleTransform(1.5f,0.5f);
            g.RotateTransform(45.0f,System.Drawing.Drawing2D.MatrixOrder.Append);
            //g.TranslateTransform(150.0f,50.0f,System.Drawing.Drawing2D.MatrixOrder.Append);
            g.FillRectangle(brush,rect);

            //此为验证的矩形
            Rectangle rect1 =
                new Rectangle(20, 20, 100, 100);
            g.FillRectangle(new SolidBrush(Color.Green), rect1);

            brush.Dispose();
            g.Dispose();
        }
    }
}

上面代码解封了第44行代码，使用RotateTransform顺时针旋转45度。此旋转的基础是以坐标系（0，0）进行旋转。为了进行验证，以上一个代码程序中绿色矩形的左上角坐标点（30，10）为验证，顺时针旋转45度，旋转完成后的坐标点，计算公式如下：

x=30*cos45 - 10*sin45 = 14.14;

y=30*sin45 + 10*cos45 = 28.28;

程序运行如下（注：代码中特意增加了两行验证代码，如图中绿横线和竖横线所示）：

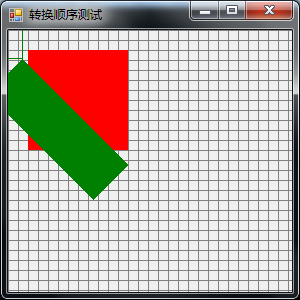
注：2022年7月24日更新

上一例代码进行scale后，结果是

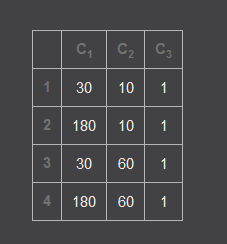
本次代码在前例的基础上旋转45度，用矩阵表示如下：

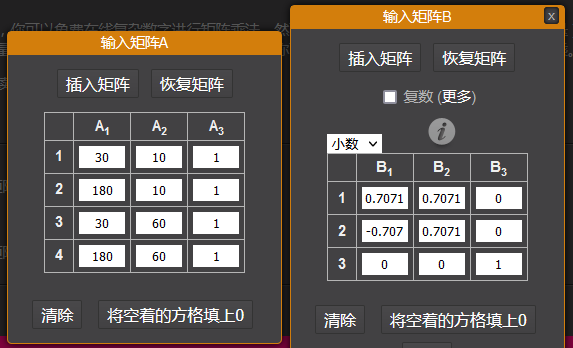
两矩阵相乘结果是：

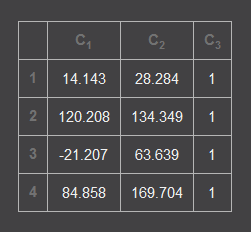
即旋转45度后，绿色矩形的四个点分别为（14.143，28.284）（120.208，134.349）（-21.207，63.639）（84.858，169.704）；从上面的效果图可以验证，这四个点位是正确的。

 

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Drawing;
using System.Windows.Forms;

namespace MatrixOrderDemo
{
    class MatrixOrderDemo:Form
    {
        static void Main(string[] args)
        {
            Application.Run(new MatrixOrderDemo());
        }
        public MatrixOrderDemo()
        {
            Text = "转换顺序测试";
        }
        protected override void OnPaint(PaintEventArgs e)
        {
            Graphics g = CreateGraphics();
            g.Clear(this.BackColor);

            Rectangle rect =
                new Rectangle(20,20,100,100);
            Brush brush = new SolidBrush(Color.Red);

            //此为绘制方格网
            for (int i = 0; i < ClientSize.Width; i +=10)
            {
                for (int j = 0; j < ClientSize.Height; j +=10)
                {
                    g.DrawLine(new Pen(Color.Gray),new Point(i,0),new Point(i,ClientSize.Height));
                    g.DrawLine(new Pen(Color.Gray),new Point(0,j),new Point(ClientSize.Width,j));
                }
            }
            g.DrawLine(new Pen(Color.Green),new PointF(14.14f,0),new PointF(14.14f,28.28f));
            g.DrawLine(new Pen(Color.Green),new PointF(0,28.28f),new PointF(14.14f,28.28f));

            g.FillRectangle(brush,rect);

            g.ScaleTransform(1.5f,0.5f);
            g.RotateTransform(45.0f,System.Drawing.Drawing2D.MatrixOrder.Append);
            g.TranslateTransform(150.0f,50.0f,System.Drawing.Drawing2D.MatrixOrder.Append);
            g.FillRectangle(brush,rect);

            //此为验证的矩形
            Rectangle rect1 =
                new Rectangle(20, 20, 100, 100);
            g.FillRectangle(new SolidBrush(Color.Green), rect1);

            brush.Dispose();
            g.Dispose();
        }
    }
}

此次代码解封的是第45行，TranslateTransform改变坐标系统的原点，将坐标原点（0，0）向右移动150，向下移动50，即为用户自定义坐标系；因上一代码示例中，绿色矩形左上角坐标为（14.14，28.28），所以新的坐标系统移动后，相对于世界坐标系，其坐标为（150+14.14=164.14，50+28.28=78.28），即（164.14，78.28），见下图（注：每个方格为10x10）

 

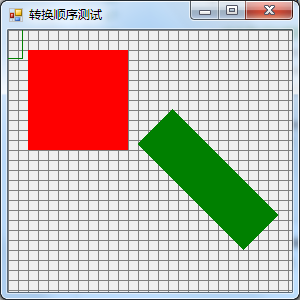
总结：TranslateTransform平移转换不受ScaleTransform影响，依然是按照世界坐标系的坐标进行平移，没有按照ScaleTransform扩大或缩小后的坐标系进行平移；