0-1背包问题——动态规划求解【Python】

动态规划求解0-1背包问题：

问题：背包大小 w，物品个数 n，每个物品的重量与价值分别对应 w[i] 与 v[i]，求放入背包中物品的总价值最大。

动态规划核心：计算并存储小问题的最优解，并将这些最优解组合成大问题的最优解。（将原问题分解为若干子问题，然后自底向上，先求解最小的子问题，把结果存储在表格中，再求解大的子问题时，直接从表格中查询小的子问题的解，避免重复计算，从而让提高算法效率）

解决本问题思路：对于第 i 个物品，放入后可以取得最大的价值，那么，前 i-1 个物品在背包容量为 w-w[i] 的情况下能够取到最大的价值。（注：因为第 i 个物品可以放入，对应要占用背包 w[i] 的容量，所以 w-w[i] 的背包容量就是前 i-1 个物品所共有的总容量）

数据结构： value[i][j] 的值表示第 i 个物品放入背包大小为 j 的背包得最大价值。

递归式：

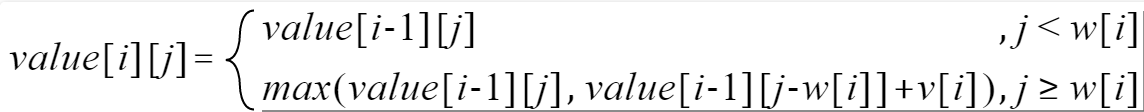
# -*- coding:utf-8 -*-
def main():

    w = int(input())    #背包大小
    n = int(input())    #物品个数

    listWV = [[0,0]]
    listTemp = []

    for i in range(n):
        listTemp = list(map(int, input().split()))  #借助临时list每次新增物品对应的list加入到listWV中
        listWV.append(listTemp) #依次输入每个物品的重量与价值

    # 建立价值数组，初始值均为0，目的是为了在value[0][j]与value[i][0]的情况为0，毕竟不放入物品或者背包容量为0的情况下，背包中的价值肯定为0，
    value = [[0 for i in range(w+1)] for j in range(n+1)]

    for i in range(1, n+1):
        for j in range(1, w+1):
            if j < listWV[i][0]:    #若物品不能放到背包中
                value[i][j] = value[i-1][j] #价值与之前相同
            else:   #物品可以放到背包中，最大价值在两者之中取
                value[i][j] = max(value[i-1][j], value[i-1][j-listWV[i][0]]+listWV[i][1])

    print(value[n][w])


if __name__ == '__main__':
    main()

检测：

10
5
2 6
5 3
4 5
2 4
3 6

17

 

上述代码只打印了最大价值，若想要打印出分别是那几个物品装入，则：

# -*- coding:utf-8 -*-
def main():

    w = int(input())    #背包大小
    n = int(input())    #物品个数

    listWV = [[0,0]]
    listTemp = []

    for i in range(n):
        listTemp = list(map(int, input().split()))  #借助临时list每次新增物品对应的list加入到listWV中
        listWV.append(listTemp) #依次输入每个物品的重量与价值

    # 建立价值数组，初始值均为0，目的是为了在value[0][j]与value[i][0]的情况为0，毕竟不放入物品或者背包容量为0的情况下，背包中的价值肯定为0，
    value = [[0 for i in range(w+1)] for j in range(n+1)]

    for i in range(1, n+1):
        for j in range(1, w+1):
            if j < listWV[i][0]:    #若物品不能放到背包中
                value[i][j] = value[i-1][j] #价值与之前相同
            else:   #物品可以放到背包中，最大价值在两者之中取
                value[i][j] = max(value[i-1][j], value[i-1][j-listWV[i][0]]+listWV[i][1])

    print(value[n][w])

    #打印放入的物品情况，需要遍历value数组
    i = n
    j = w
    listInfo = [0 for i in range(n+1)]
    while i>0:
        if value[i][j] > value[i-1][j]: #若在背包容量相同的情况下，后一个物品对应的背包价值大于了前一个物品对应的背包价值，那么说明第i个物品一定放入了背包
            listInfo[i] = 1
            j = j - listWV[i][0]
        i -= 1

    listFlag = []
    for i in range(len(listInfo)):
        if listInfo[i] == 1:
            listFlag.append(i)

    print(listFlag)


if __name__ == '__main__':
    main()

 

检测：

10
5
2 6
5 3
4 5
2 4
3 6

17
[1, 3, 5]