0-1背包问题——回溯法求解
0-1背包问题:物品总数n,每个物品的体积w[i],价值v[i],给定背包的总容量W,求放入背包中物品的最大价值。
用回溯法对0-1背包问题进行求解,具体思路是:
1.使用解空间进行标记每个物品的放入情况,即要建立一个数组进行保存其是否放入,可使用 bool x[i]进行标识;
2.回溯法第一感觉上是穷举所有情况,但事实上,有好多种情况可以进行避免,即若第t个物品放入后(即x[t]=1)已经超出背包重量,那么,在x[t]=1情况下的t+1—n个物品就不用再考虑,这样可以节省好多时间,回溯法有区别与穷举法;
3.对于解空间,用解空间数进行组织数据,解空间树的深度就是问题的规模n;
4.在解空间树中,我们用左子树、右子树分别标记1/0情况,即左子树的边代表放入,右子树的边代表不放入;
5.建立回溯函数是重中之重,回溯函数建立分三步:
1 void Backtrack(int t) 2 { 3 if(t > n){ //是否到达叶节点 4 for(int i = 1; i <= n; i++){ 5 best_x[i] = x[i]; //记录回溯的最优情况 6 } 7 best_v = now_v; //记录回溯中的最优价值 8 return; 9 } 10 if(now_w + w[t] <= W){ //约束条件,是否放入。放入考虑左子树,否则考虑右子树 11 x[t] = 1; 12 now_w += w[t]; 13 now_v += v[t]; 14 Backtrack(t+1); //进行下一个节点的分析 15 now_w -= w[t]; //在到达叶节点后进行回溯 16 now_v -= v[t]; 17 } 18 if(Bound(t+1) > best_v){ //限界条件,是否剪枝。若放入t后不满足约束条件则进行到此处,然后判断若当前价值加剩余价值都达不到最优,则没必要进行下去 19 x[t] = 0; 20 Backtrack(t+1); 21 } 22 23 }
(1)是否已经搜索到了叶节点,若已经到了叶节点,此时该分支对应的价值情况与物品分配情况已经得知,为此进行保存后返回,然后进行回溯;
(2)若没有搜索到叶节点,那么需要考虑对应物品是否可以放入背包(涉及到问题的约束条件),若可以(在树的左子树进行操作),对当前价值、当前容量进行更新,x[t]=1进行标记已经放入背包。接着进行下一个物品的分析调用该回溯函数,若是回溯函数返回,则表明已经进行到叶节点,所有情况均考虑完成,那么回溯正式开始。当前容量减去当前物品容量,当前价值减去当前物品价值,则表示当前物品没有放入背包的情况,后续执行第(3)步。
(3)若对应的物品不能放入背包,继续分析后面剩余物品的价值加上当前的价值是否会大于我们前面求得的最优价值,若后面剩余物品的价值加上当前的价值小于,则我们就没必要在进行往下考虑。否则,我们需要继续往下考虑,即将当前的物品x[t]=0进行标记,接着对下一个物品调用回溯函数。
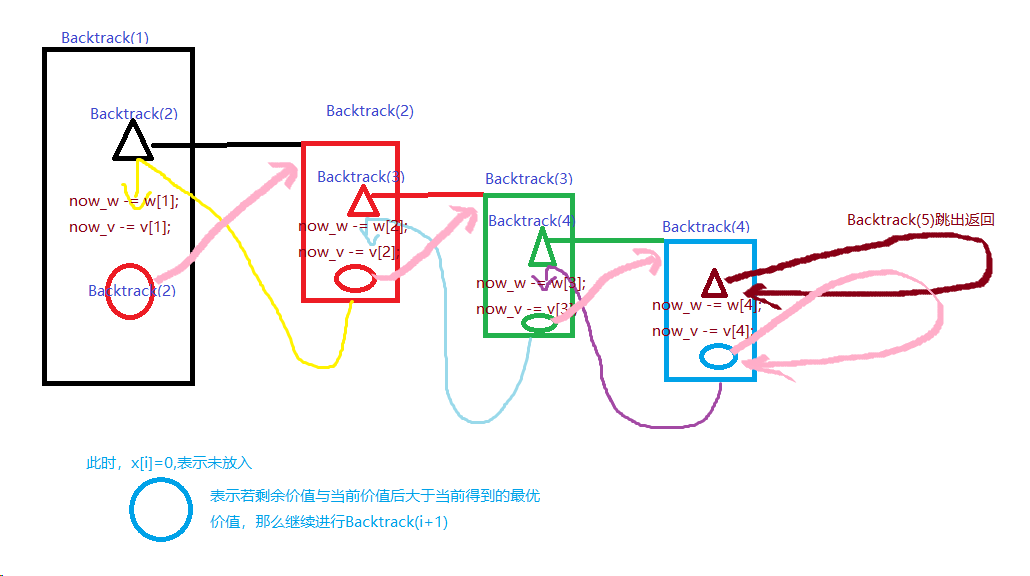
上述递归函数有些绕,其实就是在没有搜索到叶节点的情况下,判断是否可以放入背包,若可以,放入,继续往下进行,若不可以,则判断剩余的全部放入背包是否比当前得到的最优值更好,若没有当前最优值好,则pass。回溯也用到了递归,首先是距离根节点最远的开始回溯,最远的情况执行完毕返回到次远分析,最后分析到根节点。
1 #include <iostream> 2 #define N 100 3 using namespace std; 4 int n; 5 double W; 6 double w[N]; 7 double v[N]; 8 bool x[N]; //用于记录某次回溯情况 9 bool best_x[N]; //存储最优回溯情况 10 double now_v; //当前价值 11 double remain_v; //剩余价值 12 double now_w; //当前容量 13 double best_v; //最优价值 14 15 double Bound(int k) 16 { 17 remain_v = 0; 18 while(k <= n){ 19 remain_v += v[k]; 20 k++; 21 } 22 return remain_v + now_v; 23 } 24 25 void Backtrack(int t) 26 { 27 if(t > n){ //是否到达叶节点 28 for(int i = 1; i <= n; i++){ 29 best_x[i] = x[i]; //记录回溯的最优情况 30 } 31 best_v = now_v; //记录回溯中的最优价值 32 return; 33 } 34 if(now_w + w[t] <= W){ //约束条件,是否放入。放入考虑左子树,否则考虑右子树 35 x[t] = 1; 36 now_w += w[t]; 37 now_v += v[t]; 38 Backtrack(t+1); //进行下一个节点的分析 39 now_w -= w[t]; //在到达叶节点后进行回溯 40 now_v -= v[t]; 41 } 42 if(Bound(t+1) > best_v){ //限界条件,是否剪枝。若放入t后不满足约束条件则进行到此处,然后判断若当前价值加剩余价值都达不到最优,则没必要进行下去 43 x[t] = 0; 44 Backtrack(t+1); 45 } 46 47 } 48 49 void Knapsack(double W, int n) 50 { 51 double sum_w = 0; 52 double sum_v = 0; 53 best_v = 0; 54 for(int i = 0; i < n; i++){ 55 sum_w += w[i]; 56 sum_v += v[i]; 57 } 58 if(sum_w <= W){ 59 best_v = sum_v; 60 cout << "These goods could be put in the shopping car"; 61 cout << "The best value is:" << best_v <<endl; 62 return; 63 } 64 Backtrack(1); 65 cout << "The best value is:" << best_v << endl; 66 cout << "The condiction of these goods are:" << endl; 67 for(int i = 1; i <= n; i ++){ 68 cout << i << " "; 69 cout << best_x[i] << endl; //打印所有物品的放入情况,若为1表示放入,若为0则表示不放入 70 } 71 } 72 73 int main() 74 { 75 cout << "Please input the num of goods:"; 76 cin >> n; 77 cout << "Please input the capacity of the shopping car:"; 78 cin >> W; 79 for(int i = 1; i <= n; i++){ 80 cin >> w[i] >> v[i]; 81 } 82 Knapsack(W,n); 83 return 0; 84 }
注: 代码来自陈小玉老师《趣学算法》


