最长公共子序列——动态规划求解

问题：例如：X={A,B,C,B,A,D,B}，Y={B,C,B,A,A,C}，那么，二者的最长公共子序列是{B,C,B,A}，长度为4。

我们首先需要搞清楚以下两个概念：

最长公共子序列 VS 最长公共子串：

找两个字符串的最长公共子串，这个子串要求在原字符串中是连续的。而最长公共子序列则并不要求连续。

上述问题中的最长公共子序列与最长公共子串是一样的。

但是再举例X={A,B,C,B,A,D,B}，Y={B,C,B,A,A,B}，二者的最长公共子序列是{B,C,B,A,B}，而二者的最长公共子串是{B,C,B,A}。

 

求解思路：

1.分析最优解的结构特征：

设Zk={z1,z2,z3,......zk}是Xm={x1,x2,x3,......xm}和Yn={y1,y2,y3,......yn}的最长公共子序列。

则可以得到：

若xm=yn=zk，那么Zk-1={z1,z2,z3,......zk-1}是Xm-1={x1,x2,x3,......xm-1}和Yn-1={y1,y2,y3,......yn-1}的最长公共子序列；

若xm≠yn，xm≠zk，则去除xm后，Zk={z1,z2,z3,......zk}仍然是Xm-1={x1,x2,x3,......xm-1}和Yn={y1,y2,y3,......yn}的最长公共子序列；

若xm≠yn，yn≠zk，则去除yn后，Zk={z1,z2,z3,......zk}仍然是Xm={x1,x2,x3,......xm}和Yn-1={y1,y2,y3,......yn-1}的最长公共子序列；

2.建立最优值的递归式

数据结构选择：

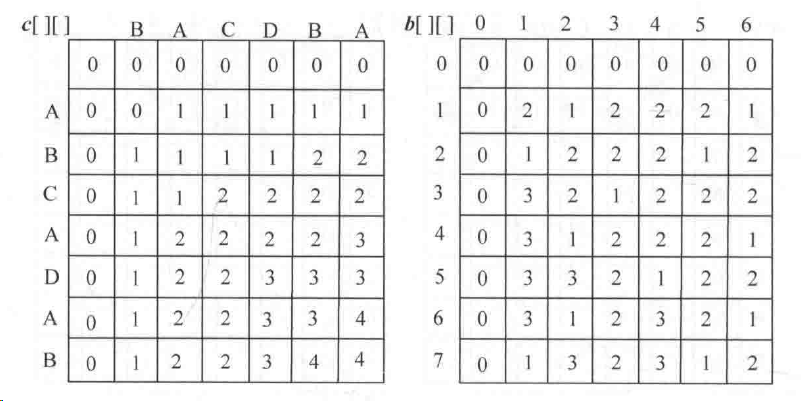
用c[i][j]表示Xi和Yj的最长公共子序列长度（这一步很关键，越到右下角，值会越来越大，我们最后只需要选取右下角的值就可以确定最长公共子序列的长度）

讨论：

若xi=yj=zk，那么c[i][j] = c[i-1][j-1] + 1；

若xi≠yj，xi≠zk，那么Xi需要进一步缩小一个长度进行匹配，即去除xi不影响整体的最长子序列变化，c[i][j] = c[i-1][j] ；

若xi≠yj，yj≠zk，那么Yj需要进一步缩小一个长度进行匹配，即去除yj不影响整体的最长子序列变化，c[i][j] = c[i][j-1] ；

结束条件，若i=0或者j=0，则c[i][j]=0。

所以，在xi≠yj的情况下，有两种情况，c[i][j]必等于两种情况下的最大值，即c[i][j] = max(c[i-1][j], c[i][j-1])

 

3.自底向上计算最优值，并记录最优值与最优策略

我们由上面可以知道，c[0][j]=0或者c[i][0]=0.

先使i = 1，则求x1与{y1,y2,y3,......yn}逐一比较。如图，x1≠y1，执行c[1][1] = max(c[0][1], c[1][0])  =0，接着，x1=y2，则执行，c[1][2] = c[0][1] + 1=1 ，接着，x1≠y3，则执行c[1][3] = max(c[0][3], c[1][2])  =1，......这样就求出了X1与Yn的最长公共子序列长度；

 

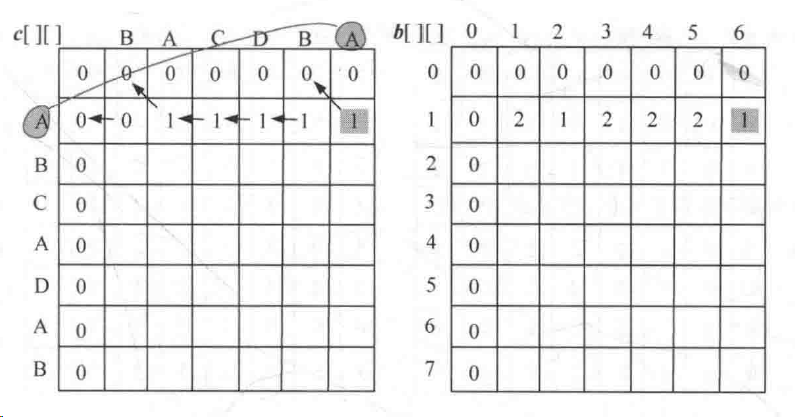
然后，i = 2，则建立在x1比较的基础上就可以求出{x1,x2}与{y1,y2,y3,......yn}的最长公共子序列长度；

 

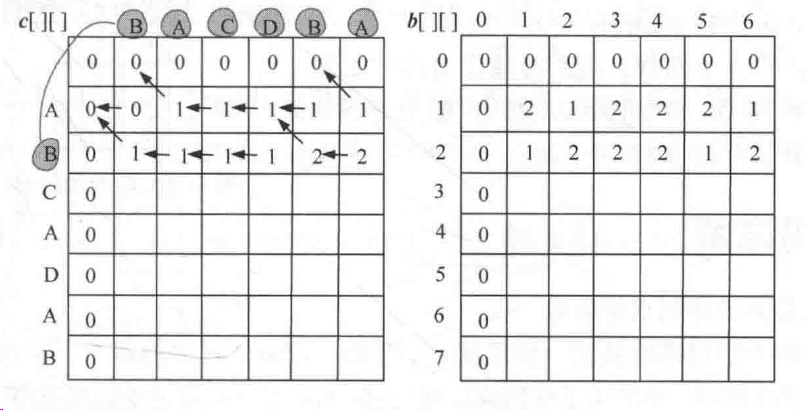
然后，i = 3，建立在{x1,x2}的基础上，则可以求出{x1,x2,x3}与{y1,y2,y3,......yn}的最长公共子序列长度；

......

然后，i = m，建立在{x1,x2,......xm-1}的基础上，则可以求出{x1,x2,......xm-1}与{y1,y2,y3,......yn}的最长公共子序列长度；

4.构造最优解

在知道了最长公共子序列的长度之后，我们还需要知道最长公共子序列中都是哪些元素。我们在c[i][j]数组的右下角能够得到最长公共子序列的长度，那么，我们可以反向推出这个元素分别是什么。

由上述，我们可以得到：

若xi=yj=zk，c[i][j] = c[i-1][j-1] + 1；

若xi≠yj，xi≠zk，c[i][j] = c[i-1][j] ；

若xi≠yj，yj≠zk，c[i][j] = c[i][j-1] ；

所以，c[i][j]由上述三个等式中的一个得到，那么我们只需要记录下c[i][j]是从三个等式中哪一个得到的，那么对应的元素我们就知道了。

这样，我们就必须在借助一个数组就行保存了，我们建立新的数组b[i][j]来记录是从哪个等式中得到，即构造出下列结构。

若xi=yj=zk，c[i][j] = c[i-1][j-1] + 1，则b[i][j] = 1，那么我们就可以取出xi或者yj作为最长公共子序列中的元素；

若xi≠yj，yj≠zk，c[i][j] = c[i][j-1]，则b[i][j] = 2，那么我们就可以去追踪c[i][j-1]；

若xi≠yj，xi≠zk，c[i][j] = c[i-1][j] ，则b[i][j] = 3，那么我们就可以去追踪c[i-1][j]；

追踪到i=0或者j=0，停止，如下图则是根据c[i][j]取值的来源将b[i][j]数组补充完整

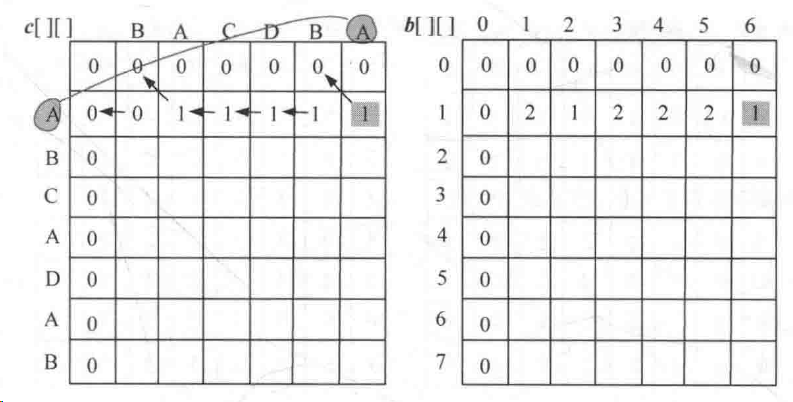
下图为两个序列的最终比较情况：我们由上述构造b[i][j]的方法得知，若 b[i][j]= 2，那么我们去追踪c[i][j-1]，若b[i][j]= 3，那么我们去追踪c[i-1][j]，换言之，就是b[i][j]= 2，就往左找，b[i][j]= 3，就往右找，若b[i][j]= 1，就可以输出此时的xi或者yj；

 

上面图片全部来自于 陈小玉老师的《趣学算法》，很好的一本书，值得大家看。

 

上述的思路理解清楚了，我们就可以上代码了，代码如下：

#include <iostream>
#include <cstring>
using namespace std;
const int N=1024;
int c[N][N],b[N][N];
char s1[N],s2[N];
int len1,len2;
void LCS()
{
    for(int i = 1; i <= len1; i++){
        for(int j = 1; j <= len2; j++){
            if(s1[i-1] == s2[j-1]){ //注：此处的s1与s2序列是从s1[0]与s2[0]开始的
                c[i][j] = c[i-1][j-1] + 1;
                b[i][j] = 1;
            }
            else{
                if(c[i][j-1] >= c[i-1][j]){
                    c[i][j] = c[i][j-1];
                    b[i][j] = 2;
                }
                else{
                    c[i][j] = c[i-1][j];
                    b[i][j] =3;
                }
            }
        }
    }
}

void LCS_PRINT(int i, int j)
{
    if(i==0 || j==0){
        return;
    }
    if(b[i][j] == 1){
        LCS_PRINT(i-1,j-1);
        cout << s1[i-1];
    }
    else if(b[i][j] == 2){
        LCS_PRINT(i,j-1);
    }
    else{
        LCS_PRINT(i-1,j);
    }
}

int main()
{
    cout << "请输入X字符串" << endl;
    cin >> s1;
    cout << "请输入Y字符串" << endl;
    cin >> s2;
    len1 = strlen(s1);
    len2 = strlen(s2);
    for(int i = 0; i <= len1; i++){
        c[i][0] = 0;
    }
    for(int j = 0; j <= len2; j++){
        c[0][j] = 0;
    }
    LCS();
    cout << "s1与s2的最长公共子序列的长度是：" << c[len1][len2] <<endl;
    cout << "s1与s2的最长公共子序列是：";
    LCS_PRINT(len1,len2);
    return 0;
}