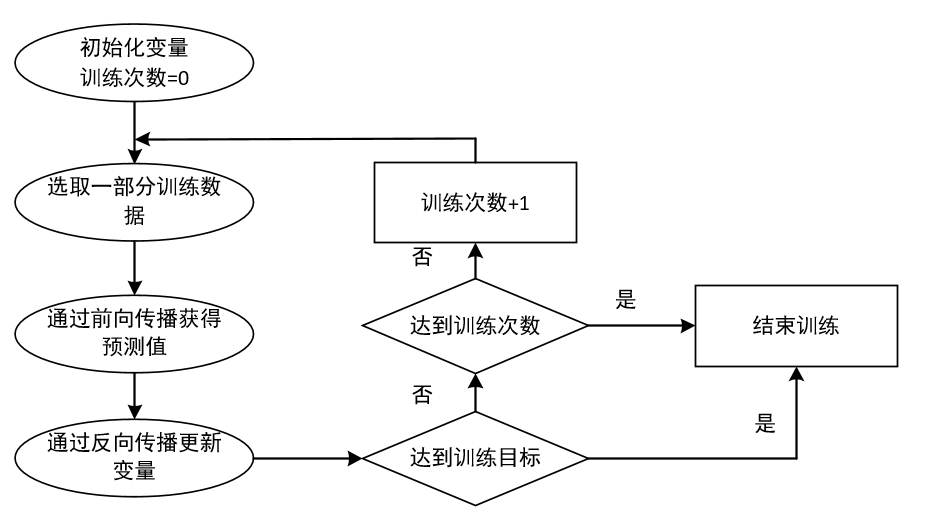
神经网络训练的过程
神经网络训练的过程可以分为三个步骤
1.定义神经网络的结构和前向传播的输出结果
2.定义损失函数以及选择反向传播优化的算法
3.生成会话并在训练数据上反复运行反向传播优化算法
神经元
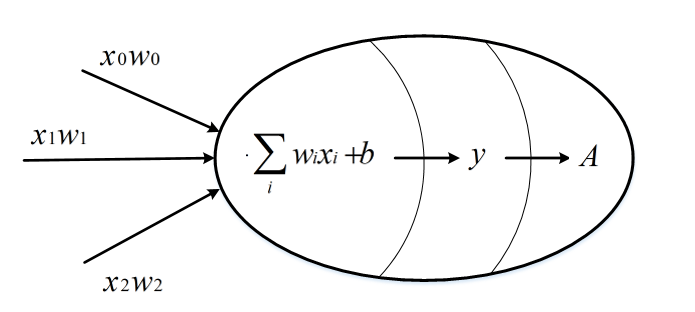
神经元是构成神经网络的最小单位,神经元的结构如下
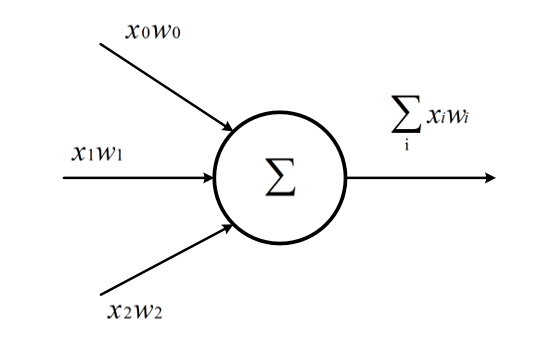
一个神经元可以有多个输入和一个输出,每个神经元的输入既可以是其他神经元的输出,也可以是整个神经网络的输入。
上图的简单神经元的所有输出即是所有神经元的输入加权和,不同输入的权重就是神经元参数,神经网络的优化过程就是优化神经元参数取值的过程。
全神经网络
全连接神经网络相邻两层之间任意两个节点都有连接
三层全连接神经网络
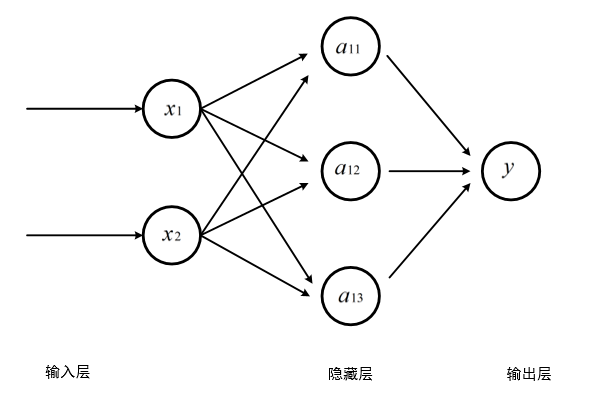
输入层从实体提取特征向量,隐藏层越多,神经网络结构越复杂
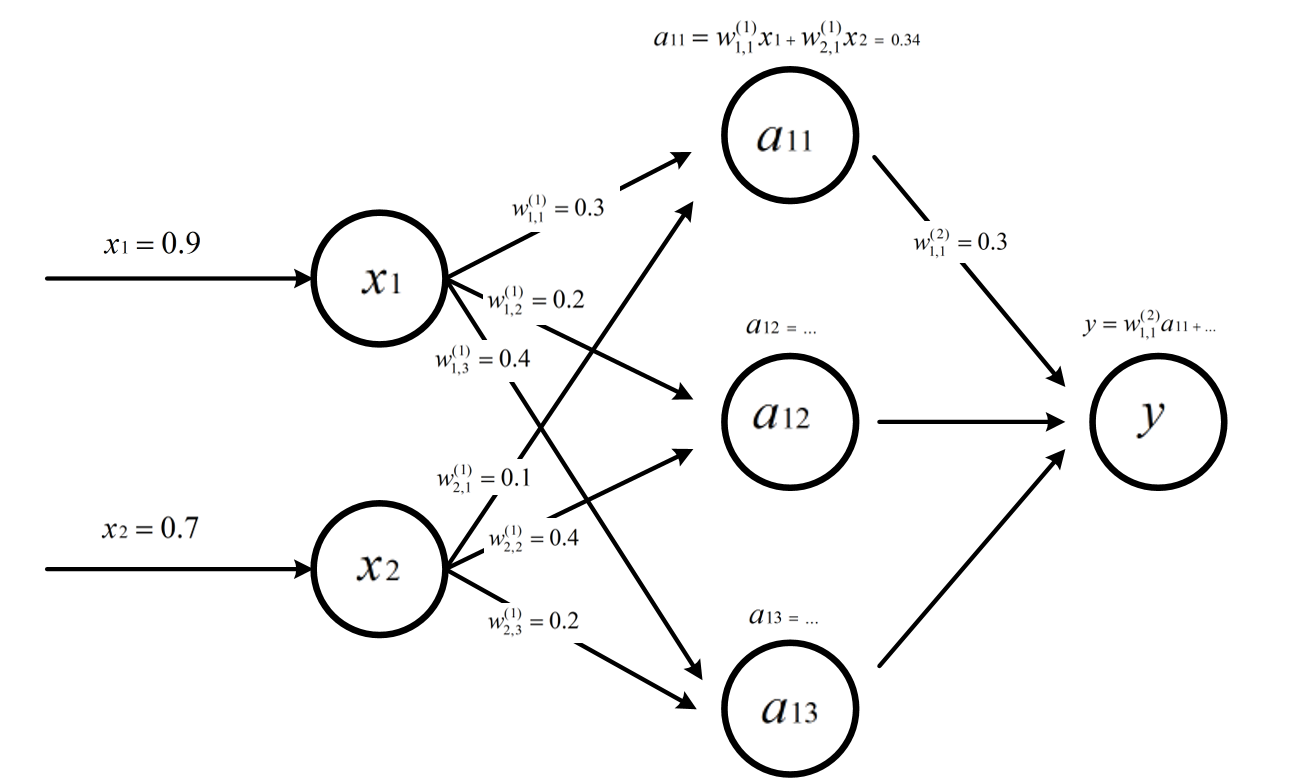
我们给上图的神经网络添加参数
-
W表示神经元的参数,上标为神经网络的层数,下标为连接节点标号,W的数值就为当前边上的权重。
-
隐藏层的a11的值就为对应的输入值的加权和
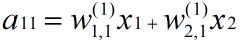
-
输出y就是隐藏层的三个值的加权和

线性模型
如果模型的输出为输入的加权和,输出y和输入xi满足如下关系,则这个模型就是线性模型
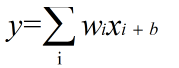
wi,b∈R是模型的参数,当输入只有一个的时候x和y就形成了一个二维坐标系的一条直线。
当有n输入时,就是一个n+1维空间的平面。
在现实世界中,绝大部分问题是无法线性分割的。如果我们不运用激活函数的话,则输出信号将仅仅是一个简单的线性函数。
我们需要激活函数帮助我们理解和学习其他复杂类型的数据。
激活函数去线性化
如果将每一个神经元的输出通过一个非线性函数,则整个神经网络的模型也就不再是线性的了。
整个非线性函数就是激活函数。
损失函数
神经网络模型的效果及优化的目标是通过损失函数来定义的
监督学习
监督学习的思想就是在已知答案的标注数据集上,模型给出的结果要尽量接近真实的答案。通过调整神经网络中的参数
对训练数据进行拟合,使得模型对未知的样本提供预测能力。
反向传播算法
反向传播算法实现了一个迭代的过程,每次迭代开始的时候,先取一部分训练数据,通过前向传播算法
得到神经网络的预测结果。因为训练数据都有正确的答案,所以可以计算出预测结果和正确答案之间的差距。
基于这个差距,反向传播算法会相应的更新神经网络参数的取值,使得和真实答案更加接近。