训练神经网络的过程中主要概念-学习笔记

• 神经网络训练过程可以分为三个步骤

1.定义神经网络的结构和前向传播的输出结果

2.定义损失函数以及选择反向传播优化的算法

3.生成会话并在训练数据上反复运行反向传播优化算法

神经网络的结构

神经元

神经元是构成神经网络的最小单位，神经元结构如下：

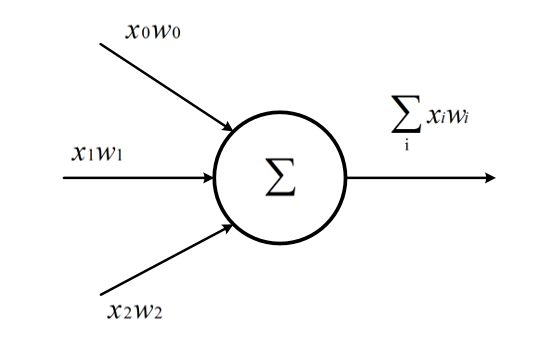
一个神经元有多个输入和一个输出，每个神经元的输入既可以是其他神经元的输出也可以是整个神经网络的输入。

如图所示的简单神经元的所有输出即是所有神经元输入的加权和，不同输入的权重就是神经元参数（wi），神经元的优化过程就是优化神经元参数取值的

过程。

全连接神经网络

全连接神经网络相邻两层之间任意两个节点都有连接。

三层全连接神经网络：

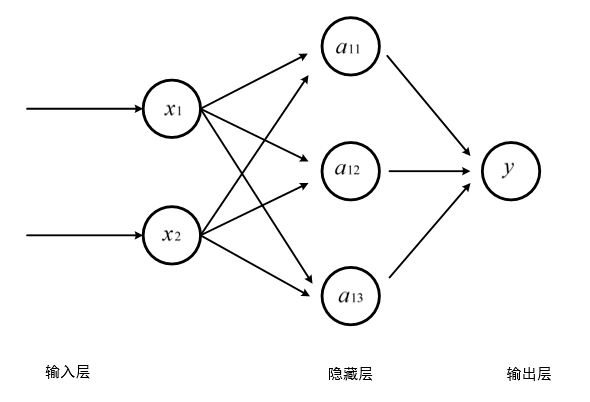
其中输入层从实体提取特征向量，隐藏层越多，神经网络结构越复杂。深层神经网络即是一类通过多层非线性变换对高复杂性数据建模算法的合集。

前向传播

前向传播就是输出通过一层层隐藏层的运算最终得到输出层的过程。

前向传播过程：

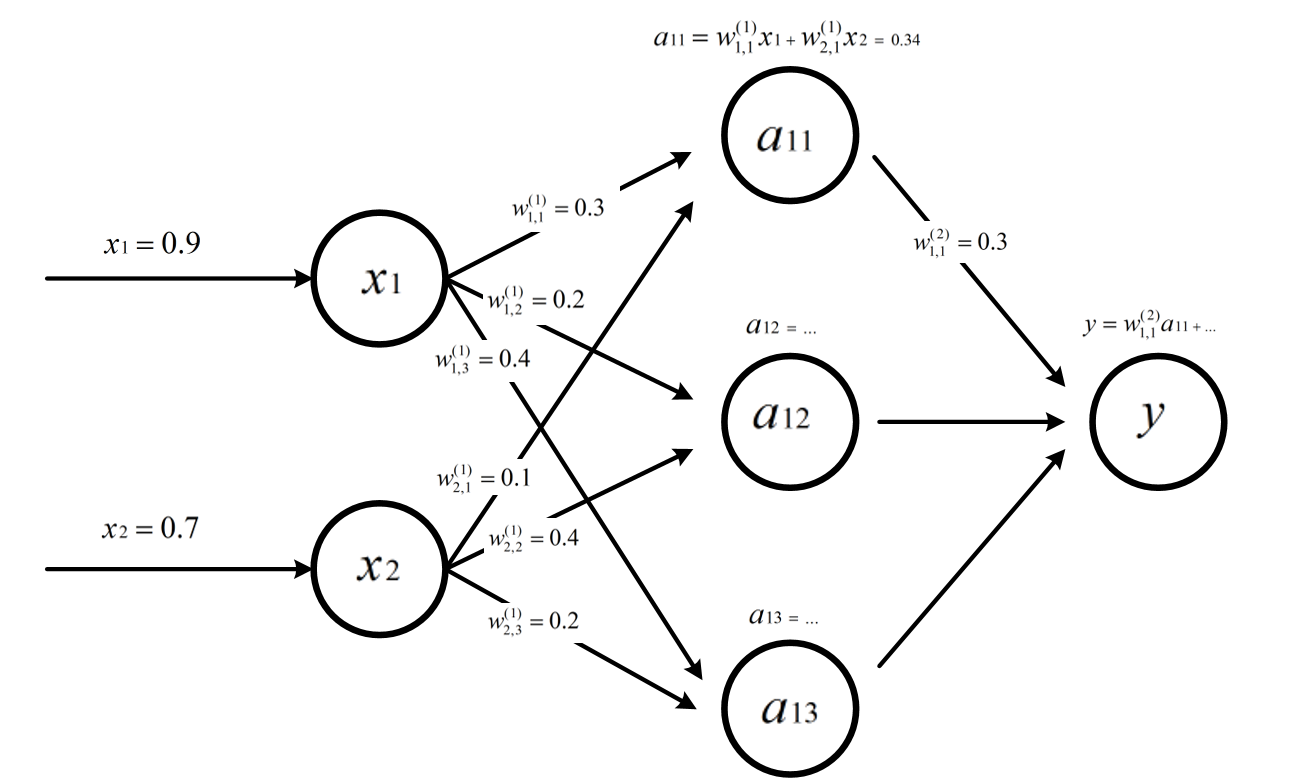
x1和x2为神经网络的输入，W表示神经元的参数，上标为神经网络的层数，下标为连接节点标号，W的数值就为当前边上的权重。

因为这个神经网络的输出为神经元输入的加权和，所以

a11：

y：

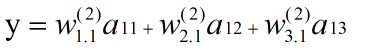
激活函数

上述的模型就是一个简单的线性模型，输入和输出满足线性模型的关系式

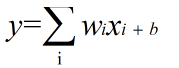
wi,b∈R是模型的参数，当输入只有一个的时候x和y就形成了一个二维坐标系的一条直线。当有n输入时，就是一个n+1维空间的平面。

但是在现实世界中，绝大部分问题是无法线性分割的。如果我们用线性模型的话，输出信号将仅仅是一个简单的线性函数。

我们需要借助非线性函数帮助我们理解和学习其他复杂类型的数据，这个函数就是激活函数。

激活函数去线性化

如果将每一个神经元的输出通过一个非线性函数，则整个神经网络的模型也就不再是线性的了。

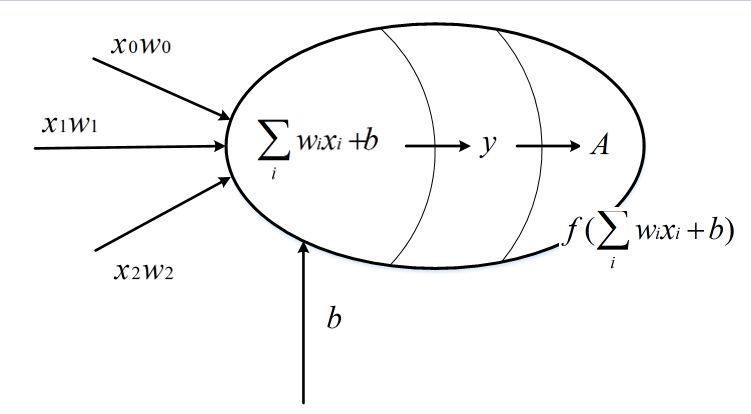
这里y到A的过程就是通过激活函数去线性化。改变主要有两个，一个是增加了偏置项（bias），一个是在原来的线性输出的基础上做了一个非线性变换f。

损失函数

在有监督的学习中，需要衡量神经网络输出和所预期的输出之间的差异大小。这种误差函数需要能够反映出当前网络输出和实际结果之间一种量化之后的不一致程度，也就是说函数值越大，反映出模型预测的结果越不准确。这种误差函数就是损失函数。

神经网络模型的效果及优化的目标是通过损失函数来定义的。

监督学习的思想就是在已知答案的标注数据集上，模型给出的结果要尽量接近真实的答案。通过调整神经网络中的参数
对训练数据进行拟合，使得模型对未知的样本提供预测能力。

反向传播算法

反向传播算法实现了一个迭代的过程，每次迭代开始的时候，先取一部分训练数据，通过前向传播算法

得到神经网络的预测结果。因为训练数据都有正确的答案，所以可以计算出预测结果和正确答案之间的差距。

基于这个差距，反向传播算法会相应的更新神经网络参数的取值，使得和真实答案更加接近。

反向传播算法流程图：

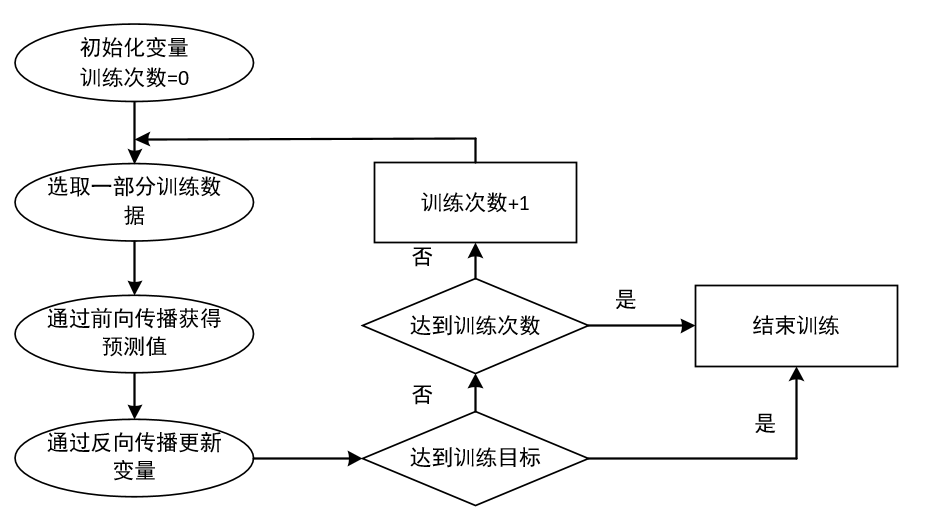
通俗的理解就是我们玩过的弹弹堂。

我们通过调整角度和力度来发射炮弹去击中目标，假设没有风力其他外界因素的影响。

我们第一次发射之后打偏了打在了目标前方，在第二次的时候我们就会适当加大力度、向下调整角度，反复几次之后我们就会掌握到合适的力度和角度。

• 每次的击中点和目标的差距就是误差，可以用一个损失函数来表示。

• 每一次发射之后查看击中点的位置，然后进行力度及角度的调整，这个过程就是反向传播。

梯度下降算法

阶梯下降算法主要用于优化单个参数的取值，反向传播算法则是给出了一个高效的方式在所有的参数上使用梯度下降算法。