ML- 线性回归推导

线性回归, 这部分算是我最为擅长的了, 真的不吹, 6年经验, 我高中时代就已经会推导了, 当然是最最小二乘法和统计学(假设检验, 参数分布等)的角度.

后来上了大学, 又是从最小二乘和统计学角度, 最终呢, 还是从线性代数(向量投影) 和 微积分 角度 + 代码实现给整了一遍, 再后来就是ML, 撸了一遍梯度下降, 嗯, 整体感悟就是,对一个事物的认知, 需要一个时间的过程和实践.

正如古人所讲, 纸上来得终觉浅, 绝知此事要躬行.

回归模型

数据:

\((y_i, X_{i1}, X_{i2}...X_{ip}), \ i = 1,2,3...n\)

y 是一个向量, X是一个矩阵

样本 X 是一个 nxp 的矩阵, 每一行是表示一个样本, 对应一个目标值

y 是由这 p 个(维) 列向量 线性组合 而成, 因此叫线性回归.

模型:

\(y_i = \beta_0 +\beta_1 X_{i1} + \beta_2 X_{i2} + \beta_p X_{il} + \epsilon_i, \ i=1,2,...n\)

\(\epsilon \backsim N(0, \sigma)\) , 为啥误差的均值是0, 参考大数定律呗.(总体和样本的关系)

写为矩阵的形式:

\(y = X\beta + \epsilon\)

X 是 nxp, \(\beta\) 是 px1, y 是 nx1

误差函数:

\(J(\beta) = ||X\beta - y||^2\)

\(X\beta - y\) 表示两个列向量相减, 表示两个向量 相似, 如果相似, 则对应的分量应该接近0, 这样得到的差向量, 对其求模, 就可衡量了.

当然, 之前在SVM 衡量相似 用的是 内积, 方法很多啦, 可解释就好.

最线性代数(投影)求解 \(\beta\)

涉及的现代知识有些多,不过这是必须的, 当你认识到本质的时候, 你会发现, 原来世界如此美妙.
这是为方便说明投影概念,我在2017年画的几张图.

\(\beta = (X^TX)^{-1}X^Ty\)

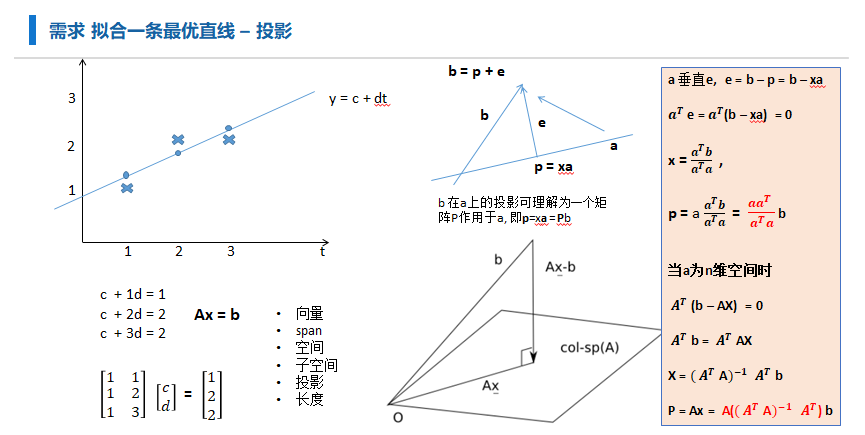
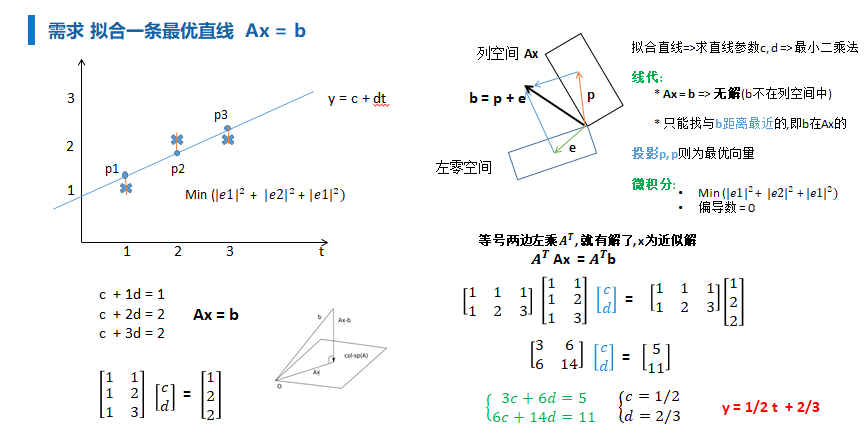
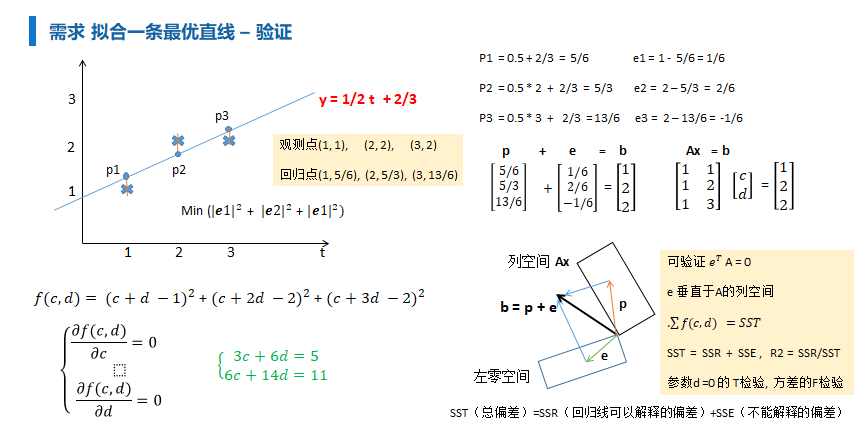
从向量投影角度: 参考MIT <线性代数> 最小二乘

\(y = X\beta\) 无解, 做一个变换, 等号两边左乘 \(X^T\) 求近似解(空间投影找近似)

\(X^Ty = X^TX\beta\)

$即: \beta = (X^TX)X^Ty $

感觉这是一个历史问题, 最小二乘在17-18世纪是非常火的, 但也是受到很多怀疑, 于是高斯这批人,就从概率的角度, 再对最小二乘法进行了一个推广, 也就差不多时大二的概率论书中的那个样子, 用似然来整的.

从微分(梯度)角度求解 \(\beta\)

\(J(\beta) = ||X\beta -y||^2\)

$ = (X\beta -y)^T (X\beta -y)$

\(= (\beta^T X^T -y^T) (X\beta -y)\)

\(=\beta^T X^T X \beta - \beta^T X^Ty - y^TX \beta + y^Ty\)

然后对 beta 求 偏导 = 0 即可

矩阵求导: http://www2.imm.dtu.dk/pubdb/views/publication_details.php?id=3274

矩阵求导讲起来有点复杂, 我目前都是记住了一些常用的形式的, 哈哈, CV 调参侠 一枚

\(\nabla_\beta J(\beta) = 0 = 2X^TX \beta - X^Ty - X^Ty\)

\(即X^TX\beta = X^Ty\)

$即: \beta = (X^TX)X^Ty $

矩阵来写确实很优美简洁, 但有些抽象,尤其是求导, 这样还有啥好处呢? 当然是非常容易写代码了呀

人们来理解矩阵是非常困难的 - 涉及很多思想和求解

but

计算机理解矩阵是非常容易的 - 就是多维数组而已啦

只需一行代码求解 参数 beta

def 求解线性回归_beta(A, b):
    """return 值 = (𝑨^𝑻 𝑨)^(−𝟏)𝑨^𝑻 b
       A 是样本矩阵
       b 是观测的y值
    """
    return np.dot(np.dot(np.dot(A.T, A).I, A.T), b.T)

当然, 后面会再来和 梯度下降来整一波.

从概率论认识线性回归

模型:

\(y_i = \beta^Tx_i + \epsilon_i​\)

引入最大似然:

希望: \(x_i \ 在, \beta, \sigma\) 的约束下, 观察的 yi 出现的概率是最大的

同时: 误差是满足 N(0, sigma) 分布的.

Maximum Likehood: \(P(y_i | x_i, \beta, \sigma) = \frac {1}{\sigma \sqrt {2 \pi}} e ^{\frac {-(y_i - \beta^Tx_i)^2}{2 \sigma^2}}\)

我们希望收集到的 y观测, 是就是在整体中出现概率最大的情况, 即要保证索引样本出现的概率是最大的,条件概率的积最大嘛. 即从总体上来考量:

\(P(y|x, \beta, \sigma) = (\frac {1}{\sigma \sqrt {2\pi}}) ^n \prod \limits_i ^n e ^{\frac {-(y_i - \beta^Tx_i)^2}{2 \sigma^2}}\)

化简一波 连乘 两边取log (以e为底哈) 实现 乘法变为加法

why log?

求解上: 概率值是 0-1 之间, 这样连续乘的话接近0, 计算机表示数有"精度", 存不了

美观上: 用log 的性质, 能够将 乘法 转为 加法 , 方便后续推导和理论的美观

\(log[P(y|x, \beta, \sigma)] = log[(\frac {1}{\sigma \sqrt {2\pi}}) ^n \prod \limits_i ^n e ^{\frac {-(y_i - \beta^Tx_i)^2}{2 \sigma^2}}]\)

\(=log[(\frac {1}{\sigma \sqrt {2\pi}}) ^n + \sum \limits_i ^n \frac {-(y_i - \beta^Tx_i)^2}{2 \sigma^2}]\)

即针对 \(\beta\) 最大化.

\(argmax_\beta \ log[(\frac {1}{\sigma \sqrt {2\pi}}) ^n] + \sum \limits_i ^n {\frac {-(y_i - \beta^Tx_i)^2}{2 \sigma^2}}\)

\(argmax_\beta\) 就是个记号,表示对 beta 参数优化而已

进一步发现, 要优化 \(\beta\) , 跟上面 式子的第一项 没啥关系,即:

\(argmax_\beta \sum \limits_i ^n {\frac {-(y_i - \beta^Tx_i)^2}{2 \sigma^2}}\)

因为 \(\sigma ^2\) 是正数, 关系不大, 即让 分子 \(=-(y_i-\beta^Tx_i) ^2\) 最大即可:

最终转化为:

\(arg \ min_\beta \ (y_i-\beta^Tx_i) ^2\)

写为向量的形式即:

\(arg \ min_\beta \ ||y-x\beta||^2\)

这也就证明了为啥, 最前面的误差要写为 两个向量相减的模式, 而不是想SVM那样而点积形式. 从概率来说明, 这样理论就很完善了.

微分到样本点-来求 \(\beta\)

上面通过矩阵来求导, 确实很清晰明了, 不过总感觉有些抽象, 这里在直观一点来整一遍

\(J(\beta) = \frac {1}{2n}\sum \limits _{i=1}^n (y_i - \beta^Tx_i)^2\)

1/2 就是为了求导后, 形式美观, 没啥实际意义

注意求导的链式法则哈.

\(\nabla_\beta J(\beta)= \frac {1}{n} \sum \limits _{i=1}^n (y_i - \beta ^Tx_i) \ \nabla_\beta (-\beta^Tx_i) =0\)

\(=\frac {1}{n} \sum \limits _{i=1}^n (y_i - \beta ^Tx_i) x_i\) =0

\(即: \frac {1}{n} \sum \limits _{i=1}^n y_i x_i =\frac{1}{n} \sum \limits_{i=1}^n \beta ^T<x_i x_i>\)

写为矩阵不就跟上面是一样的啦:

\(y^TX = \beta^TX^TX\)

• 两个向量 x, y 的点积就是 \(x^T y\)

• y 是 nx1; X 是 nxp; \(\beta\) 是 px1

左边 = (1xn)(nxp) -> 1xp 维

右边 = (1xp)(pxn)(nxp) -> 1xp

先对等号两边 都求转置, 不影响结果

\(X^Ty = X^TX\beta\)

\(即: \beta = (X^TX)^{-1}X^Ty\)

也是得到了同样的结果哦, 厉害吧,老铁们, 请双击一波666.

梯度下降法求\(beta\)

已经不太想解释,基础的微积分概念了, 忘了就自己翻翻大一的高数吧, 几个关键词: 多元函数, 偏导数, 梯度, 方向导数, 导数的意义, 拉格朗日乘子, 这些基本概念整清楚就能明白,为啥梯度方向是函数变化最快的方向了, 因为,方向导数呀, 不想说了. 之前网上搬运的一段代码,稍改了一点点, 能明白意思就行.

from random import random


def gradient_down(func, part_df_func, var_num, rate=0.1, max_iter=10000, tolerance=1e-5):
    """
    不依赖第三库实现梯度下降
    :param func: 损失(误差)函数
    :param part_df_func: 损失函数的偏导数向量
    :param var_num: 变量个数
    :param rate: 学习率(参数的每次变化的幅度)
    :param max_iter: 最大计算次数
    :param tolerance: 误差的精度
    :return: theta, y_current:  权重参数值列表, 损失函数最小值
    """

    theta = [random() for _ in range(var_num)]  # 随机给定参数的初始值
    y_current = func(*theta)  # 参数解包

    for i in range(max_iter):
        # 计算当前参数的梯度(偏导数导数向量值)
        gradient = [f(*theta) for f in part_df_func]
        # 根据梯度更新参数 theta
        for j in range(var_num):
            theta[j] -= gradient[j] * rate  # [0.3, 0.6, 0.7] ==> [0.3-0.3*lr, 0.6-0.6*lr, 0.7-0.7*lr]

            y_current,  y_predict = func(*theta), y_current
            if abs(y_predict - y_current) < tolerance:   # 判断是否收敛, (误差值的精度)
                break

    return theta, y_current


def f(x, y):
    """原函数"""
    return (x + y - 3) ** 2 + (x + 2 * y - 5) ** 2 + 2


def df_dx(x, y):
    """对x求偏导数"""
    return 2 * (x + y - 3) + 2 * (x + 2 * y - 5)


def df_dy(x, y):
    """对y求偏导数, 注意求导的链式法则哦"""
    return 2 * (x + y - 3) + 2 * (x + 2 * y - 5) * 2


def main():
    """主函数"""
    print("用梯度下降的方式求解函数的最小值哦:")
    theta, f_theta = gradient_down(f, [df_dx, df_dy], var_num=2)

    theta, f_theta = [round(i, 3) for i in theta], round(f_theta, 3)  # 保留3位小数

    print("该函数最优解是: 当theta取:{}时,f(theta)取到最小值:{}".format(theta, f_theta))


if __name__ == '__main__':
    main()

线性回归小结

• 线性假设: 输出的y是X中各列向量的线线组合, 大前提必须是线性关系(数乘和加法), 如果不是的话, 可以转为线性关系, 如指数转对数等.

• 消除异常值: 在ml中也叫做噪声, 因为求解 \(\beta\) 是要考虑所有样本, 对对异常值特别敏感. 在特征工程的时候,就有处理好. 这跟SVM不同, SVM只要支持向量即可, 对异常值不敏感.

• 去除共线性: 如果 X 的分量是高度相关的, 这就造成过拟合了. 就是 X 的空间是不满秩的, 比如X中, 有3个字段 单价, 数量 收入, 这种就是字段冗余了, 即不满秩. 更直观地可从公式上看: $\beta = (X^TX)X^Ty $, 如果X 具有共线性, 那么 求逆 有可能出现不存在的情况.

• 高斯分布: 整个模型的假设, X, y 具有高斯分布, 这样才能进行一个可靠的预测嘛. 如果没有很好的满足正态分布, 可以适当对 X做一些变换 (log, BoxCox) 等, 使其分布更近似高斯分布

• 特征缩放: 如果先对特征进行标准化处理, 在进行训练, 那么, 该线性回归通常会有更可靠的预测效果哦.