详解KMP算法
算法介绍
字符串匹配是计算机的基本任务之一,而Knuth-Morris-Pratt算法(简称KMP)算法就是一种常见的处理字符串匹配问题的算法。
最基本最简单的字符串匹配(也就是一位一位将搜索词向后移,再从搜索词的第一位向后逐个比较)方法的时间复杂度(设字符串长度为n,搜索词长度为m)最差是O(n*m),而KMP算法的时间复杂度最差只有O(n)。
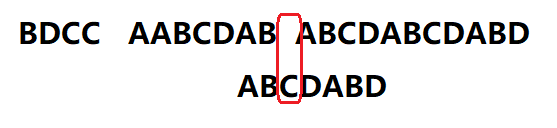
举个例子:有一个字符串”BDCC AABCDAB ABCDABCDABD”,我想知道,里面是否包含另一个字符串”ABCDABD”?
算法流程
1、
首先,将字符串”BDCC AABCDAB ABCDABCDABD”与搜索词“ABCDABD”的第一位进行比较,因为“B”与“A”不匹配所以将搜索词向后移一位
2、
继续按照上述步骤进行匹配
3、
就这样,一直找到一组匹配的字符
4、
继续匹配搜索词的第二位,发现无法匹配
先别急着将搜索词后移一位再从头逐个比较,这样有可能使效率变差,因为你要把搜索过的字符再搜索一遍
那么如何解决这个问题呢?
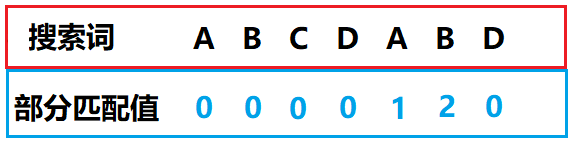
这时我需要针对搜索词算出一张《部分匹配表》(Partial Match Table)
至于这张《部分匹配表》(这张表也是KMP的关键部分)是怎样算出来的我们后面再说
已知最后一个匹配的字符是A,而A对应的部分匹配值是0,所以我们套用公式:
移动位数 = 已匹配的字符数 – 搜索词中最后一个匹配字符对应的部分匹配值
得出: 移动位数=1-0=1
也就是向后移一位
5、
我们将搜索词向后移动一位并继续匹配
发现第一位匹配成功,我们就逐个匹配搜索词的后几位
6、
直到匹配到一位不同为止
继续套用之前的公式:移动位数 = 已匹配的字符数 – 搜索词中最后一个匹配字符对应的部分匹配值
得出: 移动位数=6-2=4
于是我们将搜索词向后移4位继续匹配(这样就省去了很多无用的时间)
7、
我们继续匹配,直到再一次匹配到一样的
8、
我们依旧逐个匹配搜索词的后几位,一直到不同为止
紧接着我们算出移动位数=2-0=2
我们将搜索词向后移2位
9、
继续仿制上述的方法进行求解
补充
我们现在来介绍一下《部分匹配表》(Partial Match Table)
首先我们明确两个概念:
- 前缀:指的是字符串的子串中从原串最前面开始的子串,如abcdabd的前缀有:a,ab,abc,abcd,abcda,abcdab
- 后缀:指的是字符串的子串中在原串结尾处结尾的子串,如abcdabd的后缀有:d,bd,abd,dabd,cdabd,bcdabd
那有人会问了,这个“前缀”和“后缀”又与这个《部分匹配表》有什么关系呢?
其实这个匹配表中的每一个“部分匹配值”就是”前缀”和”后缀”的最长的共有元素的长度
比如:表中的第一个0表示“A”的”前缀”和”后缀”的最长的共有元素的长度
表中的第二个0表示“AB”的”前缀”和”后缀”的最长的共有元素的长度
表中的1表示“ABCDA”的”前缀”和”后缀”的最长的共有元素的长度
表中的2表示“ABCDAB”的”前缀”和”后缀”的最长的共有元素的长度
接下来我们以“ABCDABD”为例,算出一张《部分匹配表》:
- ”A”的前缀和后缀都为空集,最长的共有元素的长度为0;
- ”AB”的前缀为[A],后缀为[B],最长的共有元素的长度为0;
- ”ABC”的前缀为[A, AB],后缀为[BC, C],最长的共有元素的长度0;
- ”ABCD”的前缀为[A, AB, ABC],后缀为[BCD, CD, D],最长的共有元素的长度为0;
- ”ABCDA”的前缀为[A, AB, ABC, ABCD],后缀为[BCDA, CDA, DA, A],最长的共有元素为”A”,长度为1;
- ”ABCDAB”的前缀为[A, AB, ABC, ABCD, ABCDA],后缀为[BCDAB, CDAB, DAB, AB, B],最长的共有元素为”AB”,长度为2;
- ”ABCDABD”的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB],后缀为[BCDABD, CDABD, DABD, ABD, BD, D],最长的共有元素的长度为0。
代码
1 2 3 4 5 6 | for(int i=2;i<=m;i++){ //b数组是搜索串 while(j>0&&b[i]!=b[j+1])j=p[j];//好好体会这个while循环,失配的精髓。 if(b[i]==b[j+1])j++; p[i]=j;} |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | int kmp(char s,char p){ int i=0; int j=0; int sLen=strlen(s); int pLen=strlen(p); while(i<sLen && j<pLen) { //①如果j=-1,或者当前字符匹配成功(即S[i]==P[j]),都令i++,j++ if(j == -1 || s[i] == p[j]) { i++; j++; } else { //②如果j!=-1,且当前字符匹配失败(即S[i]!=P[j]),则令 i 不变,j=next[j] //next[j]即为j所对应的next值 j=next[j]; } } if(j == pLen) return i-j; else return -1;} |




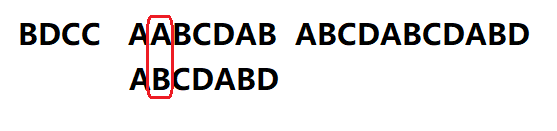
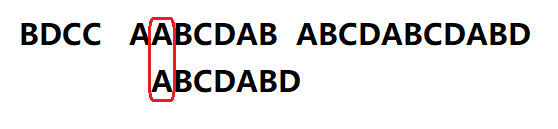
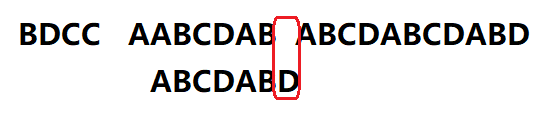








【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】