[ZJOI2006]物流运输
原题
题目描述
物流公司要把一批货物从码头A运到码头B。由于货物量比较大,需要n天才能运完。货物运输过程中一般要转停好几个码头。物流公司通常会设计一条固定的运输路线,以便对整个运输过程实施严格的管理和跟踪。由于各种因素的存在,有的时候某个码头会无法装卸货物。这时候就必须修改运输路线,让货物能够按时到达目的地。但是修改路线是—件十分麻烦的事情,会带来额外的成本。因此物流公司希望能够订一个n天的运输计划,使得总成本尽可能地小。
输入输出格式
输入格式:
第一行是四个整数n(l≤n≤100)、m(l≤m≤20)、K和e。n表示货物运输所需天数,m表示码头总数,K表示每次修改运输路线所需成本,e表示航线条数。接下来e行每行是一条航线描述,包括了三个整数,依次表示航线连接的两个码头编号以及航线长度(>0)。其中码头A编号为1,码头B编号为m。单位长度的运输费用为1。航线是双向的。再接下来一行是一个整数d,后面的d行每行是三个整数P(1<P<m),a,b(1≤a≤b≤n)。表示编号为P的码头从第a天到第b天无法装卸货物(含头尾)。同一个码头有可能在多个时间段内不可用。但任何时间都存在至少一条从码头A到码头B的运输路线。
输出格式:
包括了一个整数表示最小的总成本。总成本=n天运输路线长度之和+K*改变运输路线的次数。
输入输出样例
说明
【样例输入说明】
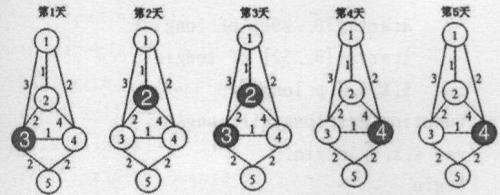
上图依次表示第1至第5天的情况,阴影表示不可用的码头。
【样例输出说明】
前三天走1-4-5,后两天走1-3-5,这样总成本为(2+2)*3+(3+2)*2+10=32。
_NOI导刊2010提高(01)
分析
当我们到第n天的时候,有两种选择,一是继续原先的路,二是换一条新的路,当然,如果在这一天原先的路不能走了就必须要换一条路,然而换成什么路当然是用最短路求啦!
首先用最短路(Djikstra)预处理:
flag[i][j]=在第i个码头在第j天时能不能装卸货物
c[i][j]=从第i天到第j天的最小费用运送路线的费用
然后再用DP算出总成本:
f[i]=运送到第i天时的最小费用
f[i]=min(f[i] , f[j]+c[j+1][i]*(i-j)+k) ------------> 第j天到第i天走同一条路,并且这条路和第j-1天是不同的
注意:要用long long!!!(本人在这里卡了1个小时)
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define inf 336860180 //memset(p,20,sizeof(p))=336860180
using namespace std;
long long head[501],w[501],v[501],nxt[501],cnt;
long long n,m,k,e,d,f[501];
bool flag[501][501];
inline void add(long long x,long long y,long long z)
{
cnt++;
w[cnt]=y;
v[cnt]=z;
nxt[cnt]=head[x];
head[x]=cnt;
}
int can[501],p[501],flag2[501];
inline long long minnn()
{
long long minn=9999999999,t=-1;
for(long long i=1;i<=m;i++)
if(flag2[i]==0 && minn>p[i])
{
minn=p[i];
t=i;
}
return t;
}
inline long long dijkstra(long long x,long long y)
{
memset(can,0,sizeof(can));
memset(flag2,0,sizeof(flag2));
memset(p,20,sizeof(p));
for(long long i=1;i<=m;i++)
{
bool sign=1;
for(long long j=x;j<=y;j++) if(flag[i][j])
{
sign=0;
break;
}
if(!sign) can[i]=1;
}
long long u=1;
p[1]=0;
while(1)
{
for(long long i=head[u];i!=0;i=nxt[i])
if(!flag2[i] && !can[w[i]] && p[u]!=inf && p[w[i]]>p[u]+v[i]) p[w[i]]=p[u]+v[i];
flag2[u]=1;
if(flag2[m]) return p[m];
u=minnn();
if(u==-1) break;
}
return p[m];
}
long long c[501][501];
int main()
{
scanf("%lld%lld%lld%lld",&n,&m,&k,&e);
for(long long i=1;i<=e;i++)
{
long long x,y,o;
scanf("%lld%lld%lld",&x,&y,&o);
add(x,y,o);
add(y,x,o);
}
scanf("%lld",&d);
for(long long i=1;i<=d;i++)
{
long long o,x,y;
scanf("%lld%lld%lld",&o,&x,&y);
for(long long j=x;j<=y;j++) flag[o][j]=1;
}
for(long long i=1;i<=n;i++)
for(long long j=i;j<=n;j++)
c[i][j]=dijkstra(i,j);
f[0]=0;
f[1]=c[1][1];
for(int i=2;i<=n;i++)
{
f[i]=c[1][i]*i;
for(int j=i-1;j>=0;j--)
f[i]=min(f[i],f[j]+c[j+1][i]*(i-j)+k);
}
printf("%lld",f[n]);
return 0;
}


