Python算法学习
绪论
数据结构
数据的两种结构逻辑结构和存储结构(物理结构)
- 逻辑结构
- 线性结构
- 线性表
- 队列
- 栈
- 非线性结构
- 树形结构
- 图状结构
- 集合结构
- 线性结构
- 存储结构
- 顺序存储结构
- 链式存储结构
算法
算法是解决某一特定问题的指定描述
算法的特征
- 有穷性
- 确定性(唯一性)
- 可行性
- 输入
- 输出
算法的评价
- 正确性
- 可读性
- 健壮性
- 效率和低存储
算法的时间复杂度
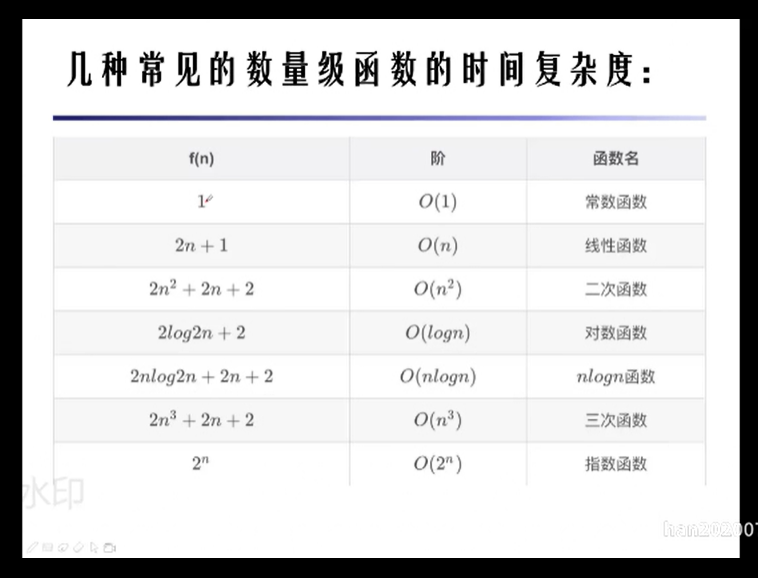
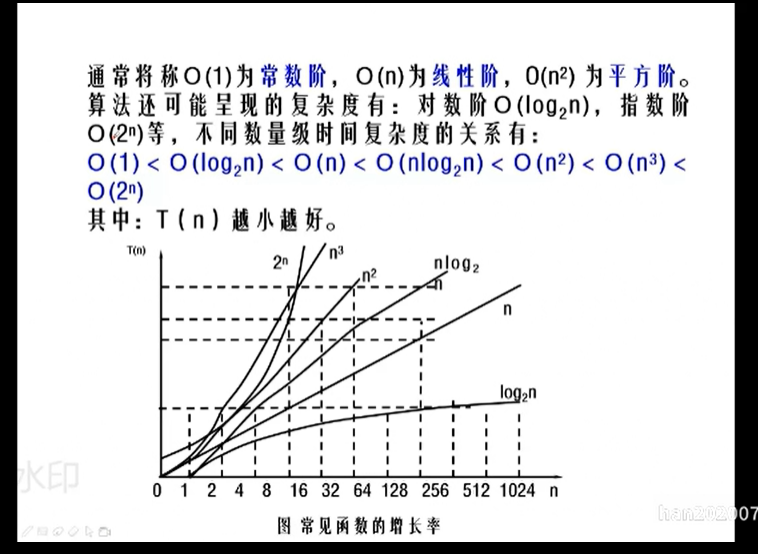
算法的空间复杂度
和时间复杂度相比不那么重要,一般算法采取的措施为用空间换时间,即用一部分的空间消耗来缩短计算时间。
递归
汉诺塔问题(递归调用)
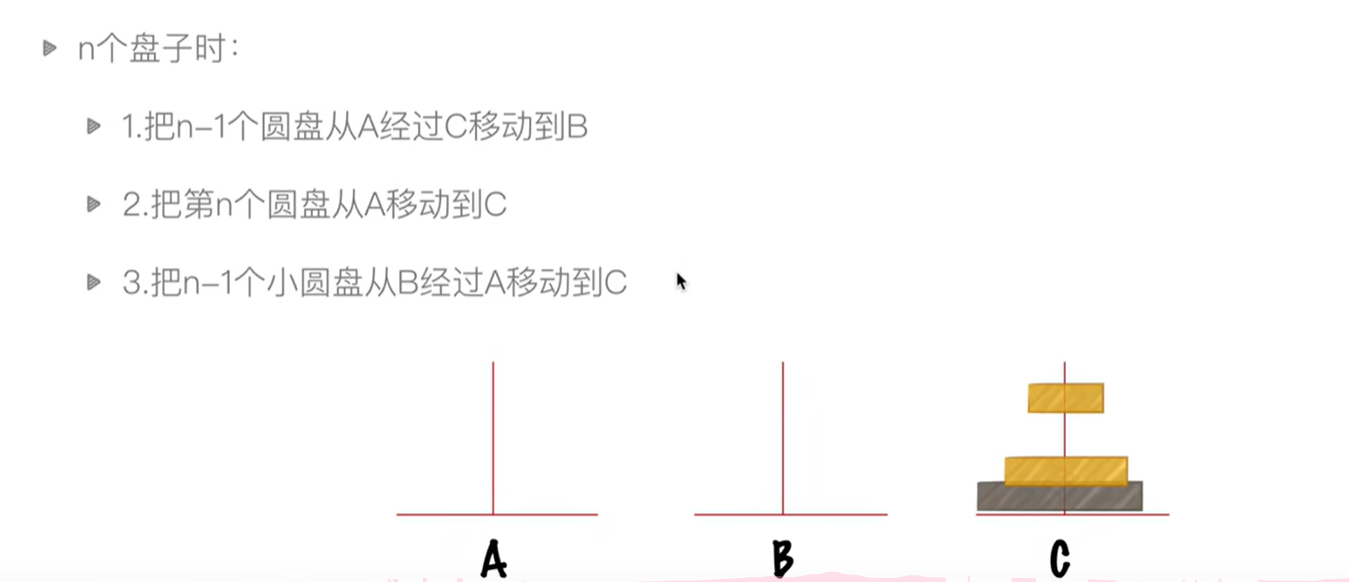
# 汉诺塔算法
def HanNoTa(n, a, b, c):
if n > 0:
HanNoTa(n - 1, a, c, b)
print(f"moving form {a} to {c}")
HanNoTa(n - 1, b, a, c)
HanNoTa(3,"A","B","C")
查找排序
二分查找
# 二分查找
def binary_search(li, val, key=1):
list_li = list(zip(list(range(len(li))), li))
if key == 1:
list_li = sorted(list_li, key=lambda x: x[1])
left = 0
right = len(list_li) - 1
while left <= right:
mid = (left + right) // 2
if list_li[mid][1] == val:
return list_li[mid][0]
elif list_li[mid][1] > val:
right = mid - 1
else:
left = mid + 1
else:
return None
a = [1, 5, 6, 2, 1, 4, 2, 6, 2, 3]
b = [1, 2, 3, 4, 5, 6, 7, 8]
ind = binary_search(a, 3)
print(ind)
ind = binary_search(b, 5, 0)
print(ind)
检查排序是否完成
def check(li, reverse=False):
if reverse == False:
for i in range(len(li) - 1):
if li[i] > li[i + 1]:
return False
else:
return True
elif reverse == True:
for i in range(len(li) - 1):
if li[i] < li[i + 1]:
return False
else:
return True
冒泡排序
# 冒泡排序
import random
def bubble_sort(li: list):
for i in range(len(li) - 1):
exchange = False
for j in range(len(li) - i - 1):
if li[j] > li[j + 1]:
li[j], li[j + 1] = li[j + 1], li[j]
exchange = True
if not exchange:
return
li = [random.randint(0, 10000) for _ in range(10)]
print(li)
bubble_sort(li)
print(li)
选择排序
# 选择排序
import random
def select_sort(li):
for i in range(len(li) - 1):
min_loc = i
for j in range(i + 1, len(li)):
if li[j] < li[min_loc]:
min_loc = j
if min_loc != i:
li[i], li[min_loc] = li[min_loc], li[i]
li = [random.randint(0, 10000) for _ in range(10)]
print(li)
select_sort(li)
print(li)
插入排序
# 插入排序
import random
def insert_sort(li):
for i in range(1, len(li)):
tmp = li[i]
j = i - 1
while j >= 0 and tmp < li[j]:
li[j + 1] = li[j]
j -= 1
li[j + 1] = tmp
li = [random.randint(0, 10000) for _ in range(10)]
print(li)
insert_sort(li)
print(li)
希尔排序(高级版插入排序)
# 希尔排序
import random
import copy
import time
def insert_sort_gap(li, gap):
for i in range(gap, len(li)):
tmp = li[i]
j = i - gap
while j >= 0 and tmp < li[j]:
li[j + gap] = li[j]
j -= gap
li[j + gap] = tmp
def shell_sort(li):
d = len(li) // 2
while d >= 1:
insert_sort_gap(li, d)
d //= 2
li = list(range(10000))
random.shuffle(li)
li1 = copy.deepcopy(li)
print(li)
print(li1)
start = time.time()
shell_sort(li)
end = time.time()
print(end - start)
print(li1)
start = time.time()
insert_sort_gap(li1, 1)
end = time.time()
print(end - start)
print(li)
print(li1)
快速排序
# 快速排序
import random
import time
# import sys
# sys.setrecursionlimit(100000) # 设置递归最大深度
def partition(li, left, right):
tmp = li[left] # 记录下最左边的数
while left < right: # 找到记录下的数的最合适的位置
while left < right and li[right] >= tmp: # 从右边找比tmp小的数的位置
right -= 1
li[left] = li[right] # 把右边较大的值写到左边的位置上
while left < right and li[left] <= tmp: # 从左边找比tmp大的数的位置
left += 1
li[right] = li[left] # 把左边较小的值写到右边的位置上
li[left] = tmp # 把记录下的数写到合适的位置
return left # 返回找到的位置
def _quick_sort(li, left, right): # 递归调用
if left < right: # 至少两个元素才进行递归调用
mid = partition(li, left, right)
_quick_sort(li, left, mid - 1)
_quick_sort(li, mid + 1, right)
def quick_sort(li):
_quick_sort(li, 0, len(li) - 1)
li = [random.randint(0, 10000) for _ in range(10000)]
print(li)
start = time.time()
quick_sort(li)
end = time.time()
print(li)
print(end - start)
堆排序(二叉树)
# 堆排序
import random
import time
def sift(li, low, high):
"""
:param li:列表
:param low: 堆的根节点的位置
:param high: 堆的最后一个元素的位置
:return: None
"""
i = low # 最开始指向根节点
j = 2 * i + 1 # j为根节点的左孩子
tmp = li[low] # 把堆顶元素存起来
while j <= high: # 建立大根堆
if j + 1 <= high and li[j + 1] > li[j]: # 如果右孩子存在并且比左孩子大
j = j + 1 # j指向右孩子
if li[j] > tmp: # 如果孩子节点大于父亲节点
li[i] = li[j] # 孩子节点元素调整到父亲节点的位置
i = j # 指针下移
j = 2 * i + 1
else: # 因为tmp比孩子节点更大,找到合适的位置
li[i] = tmp # 找到根节点合适的位置并放入
break
else:
li[i] = tmp # 把tmp放到叶子节点上
def heap_sort(li):
n = len(li)
for i in range((n - 2) // 2, -1, -1):
# i表示建堆的时候调整的部分的根的下标
sift(li, i, n - 1)
# 建堆完成
for i in range(n - 1, -1, -1):
# i指向当前堆的最后一个元素
li[0], li[i] = li[i], li[0] # 将最后一个元素与堆顶元素交换位置
sift(li, 0, i - 1) # i-1是新的high
li = [random.randint(0, 10000) for _ in range(10000)]
print(li)
start = time.time()
heap_sort(li)
end = time.time()
print(li)
print(end - start)
python中内置好的堆排序函数
# python中内置好的堆排序
import heapq
import random
li = [i for i in range(100)]
random.shuffle(li) # 打乱列表
print(li)
heapq.heapify(li) # 建堆
for i in range(len(li)):
print(heapq.heappop(li), end=",") # 弹出一个堆中最小的元素
利用堆排序解决topk问题
# 利用堆排序解决topk问题
import random
import time
def sift(li, low, high):
"""
:param li:列表
:param low: 堆的根节点的位置
:param high: 堆的最后一个元素的位置
:return: None
"""
i = low # 最开始指向根节点
j = 2 * i + 1 # j为根节点的左孩子
tmp = li[low] # 把堆顶元素存起来
while j <= high: # 建立小根堆
if j + 1 <= high and li[j + 1] < li[j]: # 如果右孩子存在并且比左孩子小
j = j + 1 # j指向右孩子
if li[j] < tmp: # 如果孩子节点小于父亲节点
li[i] = li[j] # 孩子节点元素调整到父亲节点的位置
i = j # 指针下移
j = 2 * i + 1
else: # 因为tmp比孩子节点更小,找到合适的位置
li[i] = tmp # 找到根节点合适的位置并放入
break
else:
li[i] = tmp # 把tmp放到叶子节点上
def topk(li, k):
heap = li[0:k]
for i in range((k - 2) // 2, -1, -1): # 建立小根堆
sift(heap, i, k - 1)
for i in range(k, len(li) - 1): # 遍历
if li[i] > heap[0]:
heap[0] = li[i]
sift(heap, 0, k - 1)
for i in range(k - 1, -1, -1): # 对结果排序
heap[0], heap[i] = heap[i], heap[0]
sift(heap, 0, i - 1)
return heap
li = [i for i in range(10000)]
random.shuffle(li)
print(topk(li, 10))
归并排序
# 归并排序
import random
def merge(li, low, mid, high): # 对列表中mid左右两边的子列表进行排序
i = low
j = mid + 1
ltmp = []
while i <= mid and j <= high: # 左右两个子列表都有数
if li[i] < li[j]:
ltmp.append(li[i])
i += 1
else:
ltmp.append(li[j])
j += 1
while i <= mid:
ltmp.append(li[i])
i += 1
while j <= high:
ltmp.append(li[j])
j += 1
li[low:high + 1] = ltmp
def _merge_sort(li, low, high):
if low < high: # 至少有两个元素,递归
mid = (low + high) // 2
_merge_sort(li, low, mid)
_merge_sort(li, mid + 1, high)
merge(li, low, mid, high)
def merge_sort(li):
_merge_sort(li, 0, len(li) - 1)
li = [i for i in range(1000)]
random.shuffle(li)
print(li)
merge_sort(li)
print(li)
六种排序方法的总结
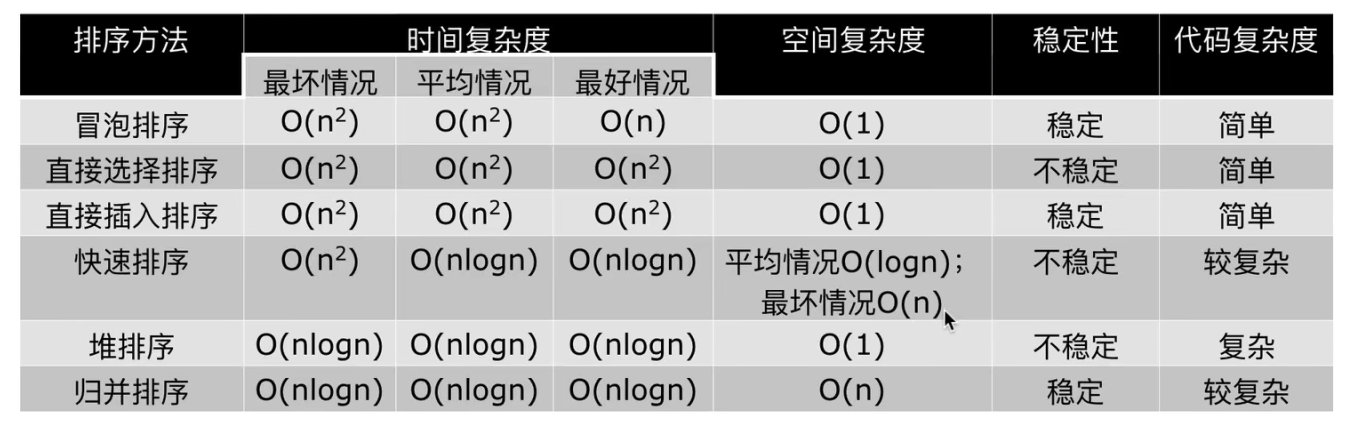
计数排序
# 计数排序
import random
def count_sort(li: list):
count = [0 for _ in range(min(li), max(li) + 1)]
min_num = min(li)
for val in li:
count[val - min_num] += 1
li.clear()
for ind, val in enumerate(count):
for i in range(val):
li.append(ind + min_num)
li = list(range(-9, 21))
random.shuffle(li)
print(li)
count_sort(li)
print(li)
桶排序(高级版计数排序)
# 桶排序
import random
def bucket_sort(li: list):
max_num = max(li)
n = max_num // 100
if n == 0:
n = 1
buckets = [[]]
else:
buckets = [[] for _ in range(n)]
for var in li:
i = min(var // (max_num // n), n - 1) # i表示var放到几号桶里
buckets[i].append(var)
for j in range(len(buckets[i]) - 1, 0, -1): # 保持桶内的顺序
if buckets[i][j] < buckets[i][j - 1]:
buckets[i][j], buckets[i][j - 1] = buckets[i][j - 1], buckets[i][j]
else:
break
li.clear()
for buc in buckets:
li.extend(buc)
return li
li = list(range(200))
li1 = list(range(200))
random.shuffle(li)
print(li == li1)
bucket_sort(li)
print(li)
print(li == li1)
基数排序
# 基数排序
import random
def radix_sort(li: list):
max_num = max(li)
it = 0
while 10 ** it <= max_num: # 求最大数的位数
buckets = [[] for _ in range(10)] # 创建桶
for var in li: # 把数放入桶中
digit = (var // 10 ** it) % 10 # 依次取每个数的位数
buckets[digit].append(var)
li.clear()
for buc in buckets:
li.extend(buc)
it += 1
li = [random.randint(0, 10000) for _ in range(1000)]
print(li)
radix_sort(li)
print(li)
print(check(li))
数据结构
线性表
列表(即顺序表)
- 列表内的每个节点储存的元素为地址,所以列表内部可以时任意数据类型
- 列表是动态分配存储空间,列表长度不够的时候,python底层会为列表重新开辟一个更大的空间,并把原先列表中存储的地址复制到新开辟的空间中
栈(后进先出)
顺序栈
列表(li)结构可以实现栈
- 进栈:li.append
- 出栈:li.pop
- 取栈顶:li[-1]
class Stack:
def __init__(self):
self.stack = []
def push(self, element):
self.stack.append(element)
def pop(self):
if len(self.stack) > 0:
return self.stack.pop()
else:
return None
def get_pop(self):
if len(self.stack) > 0:
return self.stack[-1]
else:
return None
def is_empty(self):
return len(self.stack) == 0
stack = Stack()
stack.push(1)
stack.push(2)
stack.push(3)
print(stack.pop())
print(stack.pop())
print(stack.is_empty())
print(stack.pop())
print(stack.is_empty())
print(stack.pop())
链式栈
class stack_linked():
def __init__(self, Node=None):
self.head = Node
def create(self, val):
if not self.head:
self.head = ListNode(val)
def push(self, val):
if not self.head:
self.head = ListNode(val)
return
node = ListNode(val)
node.next = self.head
self.head = node
def pop(self):
val = self.head
self.head = self.head.next
return val
stack = stack_linked()
stack.push(5)
stack.push(6)
print(stack.pop().val)
print(stack.head.val)
栈的应用
迷宫问题(找的不一定是最短路径)
map = [
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
[1, 0, 0, 0, 0, 1, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 0, 0, 0, 0, 1],
[1, 0, 0, 0, 1, 0, 0, 0, 0, 1],
[1, 0, 1, 0, 0, 0, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 0, 1, 1, 0, 1],
[1, 1, 0, 0, 0, 0, 0, 0, 0, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
]
dirs = [
lambda x, y: (x + 1, y),
lambda x, y: (x, y + 1),
lambda x, y: (x - 1, y),
lambda x, y: (x, y - 1)
]
def map_path(x1, y1, x2, y2):
stack = []
stack.append((x1, y1))
map[x1][y1]=2
while len(stack) > 0:
curNode = stack[-1]
if curNode[0] == x2 and curNode[1] == y2:
for p in stack:
print(p)
return True
for dir in dirs:
nextNode = dir(curNode[0], curNode[1])
if map[nextNode[0]][nextNode[1]] == 0:
stack.append(nextNode)
map[nextNode[0]][nextNode[1]] = 2
break
else:
map[nextNode[0]][nextNode[1]] = 2
stack.pop()
else:
print("没有路")
return False
map_path(1, 1, 8, 8)
for i in map:
print(i)
十进制转化为其他进制
# 十进制转化为其他进制
def base_conversion(val, base):
li = []
while val != 0:
li.append(val % base)
val = val // base
li.reverse()
s = ''.join(map(str,li))
return s
print(base_conversion(120, 2))
队列(先进先出)
列表(li)可以实现队列
- 入队:li.append
- 出队:li.pop(0)
- 取队头:li[0]
顺序队列
基础队列类
class Queue:
def __init__(self):
self.queue = []
def push(self, element):
self.queue.append(element)
def is_empty(self):
return len(self.queue) == 0
def pop(self):
if not self.is_empty():
return self.queue.pop(0)
else:
return None
def get_top(self):
return self.queue[0]
queue = Queue()
queue.push(1)
queue.push(2)
queue.push(3)
print(queue.is_empty())
print(queue.pop())
print(queue.get_top())
print(queue.pop())
print(queue.pop())
print(queue.pop())
print(queue.is_empty())
循环队列类
class Queue:
def __init__(self, size=100):
self.queue = [0 for _ in range(size)]
self.size = size
self.rear = 0
self.front = 0
def push(self, element):
if not self.is_filled():
self.rear = (self.rear + 1) % self.size
self.queue[self.rear] = element
else:
raise IndexError("Queue is filled")
def pop(self):
if not self.is_empty():
self.front = (self.front + 1) % self.size
return self.queue[self.front]
raise IndexError("Queue is empty")
def get_top(self):
if not self.is_empty():
return self.queue[self.rear]
else:
return None
def is_empty(self):
return self.rear == self.front
def is_filled(self):
return (self.rear + 1) % self.size == self.front
queue=Queue(5)
print(queue.is_empty())
queue.push(1)
queue.push(2)
queue.push(3)
queue.push(4)
print(queue.is_filled())
print(queue.get_top())
print(queue.pop())
print(queue.pop())
print(queue.pop())
print(queue.pop())
print(queue.pop())
内置队列
from collections import deque # 双向队列
q = deque([1, 2, 3, 4], 4)
q.append(5) # 队尾进
print(q.popleft()) # 队首出
q.clear()
q.appendleft(1) # 队首进
q.appendleft(2)
q.appendleft(3)
print(q.pop()) # 队尾出
print(q.pop())
print(q.pop())
链式队列
class Node():
def __init__(self, val=0):
self.val = val
self.next = None
class queue_linked():
def __init__(self):
self.front = None
self.rear = None
def push(self, val):
node = Node(val)
if self.front is None:
self.front = node
self.rear = node
else:
self.rear.next = node
self.rear = self.rear.next
def pop(self):
if self.front == self.rear and self.front:
node = self.front
self.front = self.rear = None
return node
else:
if not self.front:
return
node = self.front
self.front = self.front.next
return node
def peek(self):
if not self.is_empty():
return self.front.val
else:
return
def is_empty(self):
if self.front and self.rear:
return False
else:
return True
def show(self):
p = self.front
while p:
print(p.val, end=" ")
p = p.next
print()
queue = queue_linked()
queue.push(1)
queue.push(2)
queue.push(3)
print(queue.pop().val)
print(queue.pop().val)
print(queue.pop().val)
# print(queue.peek())
queue.show()
队列的应用
迷宫问题(求的是最短路径)
map = [
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
[1, 0, 0, 0, 0, 1, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 0, 0, 0, 0, 1],
[1, 0, 0, 0, 1, 0, 0, 0, 0, 1],
[1, 0, 1, 0, 0, 0, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 0, 1, 1, 0, 1],
[1, 1, 0, 0, 0, 0, 0, 0, 0, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
]
dirs = [
lambda x, y: (x + 1, y),
lambda x, y: (x, y + 1),
lambda x, y: (x - 1, y),
lambda x, y: (x, y - 1)
]
def print_path(path, map):
curNode = path[-1]
realpath = []
while curNode[2] != -1:
realpath.append(curNode[0:2])
map[curNode[0]][curNode[1]] = 2
curNode = path[curNode[2]]
realpath.append(curNode[0:2])
map[curNode[0]][curNode[1]] = 2
realpath.reverse()
for node in realpath:
print(node)
from collections import deque
import copy
def map_path_shortest(x1, y1, x2, y2, map):
map1 = copy.deepcopy(map)
queue = deque()
queue.append((x1, y1, -1))
path = []
while len(queue) > 0:
curNode = queue.popleft()
path.append(curNode)
if curNode[0] == x2 and curNode[1] == y2:
print_path(path, map)
return True
for di in dirs:
nextNode = di(curNode[0], curNode[1])
if map1[nextNode[0]][nextNode[1]] == 0:
queue.append((nextNode[0], nextNode[1], len(path) - 1))
map1[nextNode[0]][nextNode[1]] = 2
else:
print("没有路")
return False
map_path_shortest(1, 1, 8, 8, map)
for i in map:
print(i)
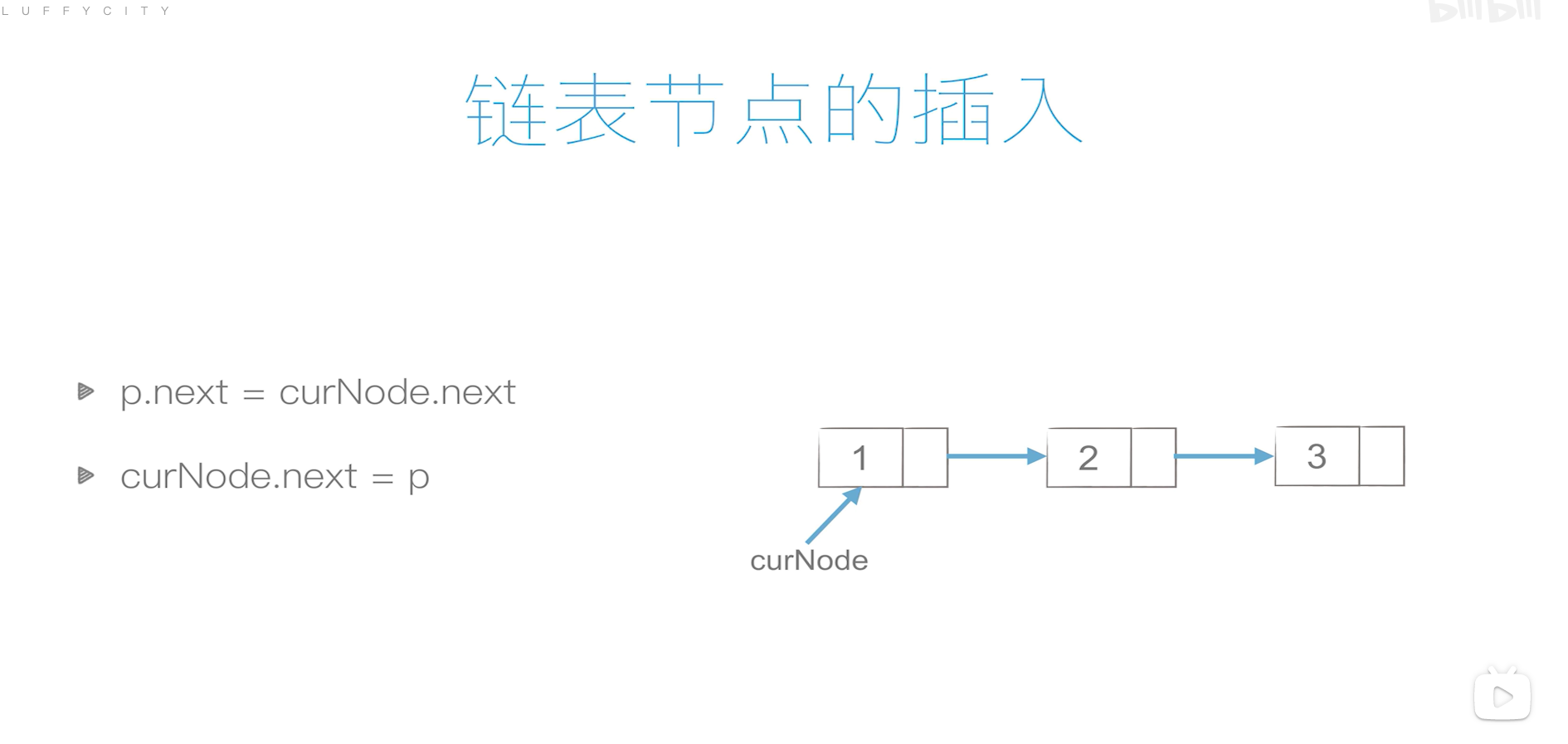
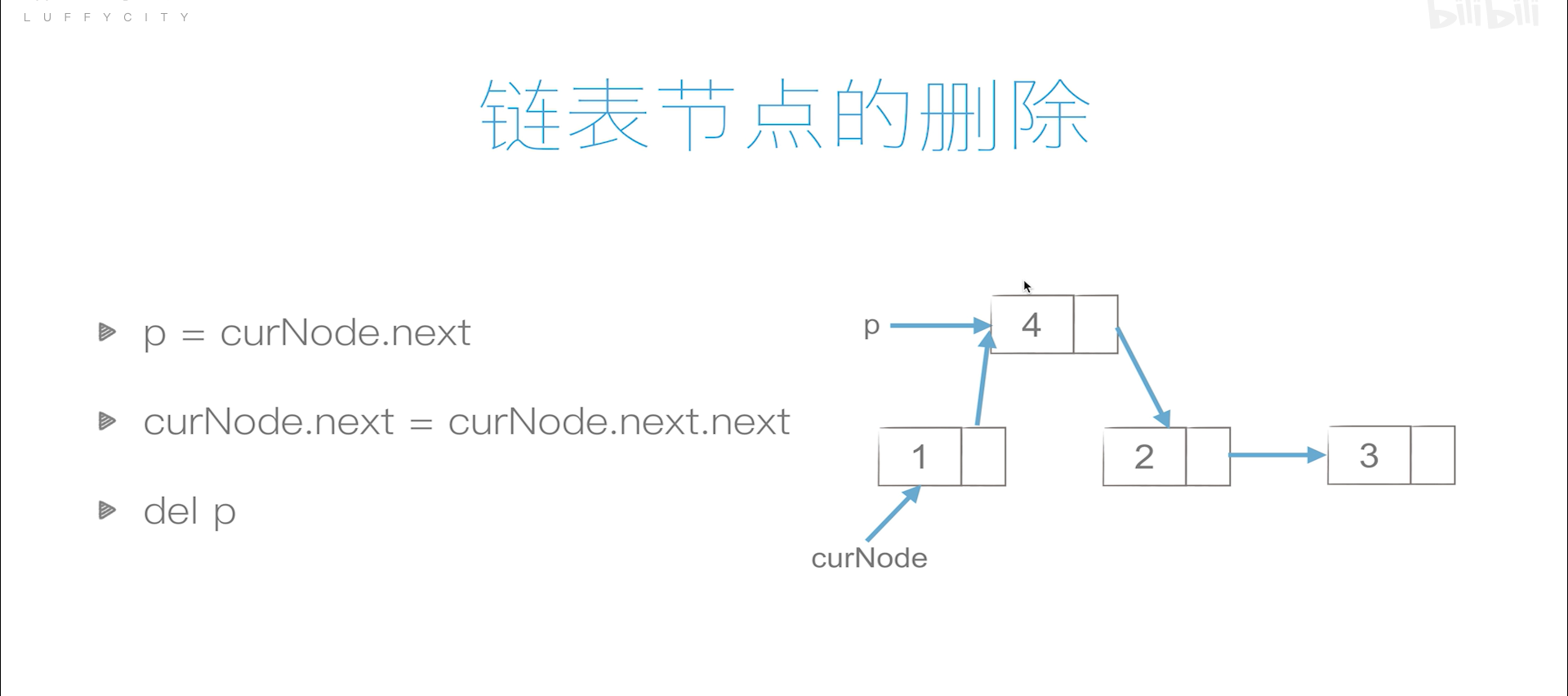
链表
单链表
单链表的创建
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
class LinkedList:
class LinkListIterator:
def __init__(self, node):
self.node = node
def __next__(self):
if self.node:
cur_node = self.node
self.node = cur_node.next
return cur_node.val
else:
raise StopIteration
def __iter__(self):
return self
def __init__(self, iterable=None):
self.head = None
self.tail = None
if iterable:
self.extend(iterable)
def append(self, obj):
s = ListNode(obj)
if not self.head:
self.head = s
self.tail = s
else:
self.tail.next = s
self.tail = s
def extend(self, iterable):
for obj in iterable:
self.append(obj)
def find(self, obj):
for n in self:
if n == obj:
return True
else:
return False
def create(self, li: list):
self.head = ListNode(li[0])
self.tail = self.head
for element in li[1:]:
node = ListNode(element)
self.tail.next = node
self.tail = node
return self.head
def create_head(self, li: list):
self.head = ListNode(li[0])
self.tail = self.head
for element in li[1:]:
node = ListNode(element)
node.next = self.head
self.head = node
return self.head
def show(self):
Node = self.head
while Node != None:
print(Node.val, end='\t')
Node = Node.next
print()
def get_length(self):
if self.head is None:
return 0
count = 1
node = self.head
while node != self.tail:
count += 1
node = node.next
return count
def get_value(self, index):
"""
:type index: int
:rtype: int
"""
if index < 0 or index >= self.get_length():
return -1
cur = self.head.next
while index:
cur = cur.next
index -= 1
return cur.val
def get_index(self, value):
count = 0
cur = self.head
while cur:
if cur.val == value:
break
count += 1
cur = cur.next
else:
return -1
return count
def addAtIndex(self, index, val):
"""
:type index: int
:type val: int
:rtype: None
"""
if index <= 0:
node = ListNode(val)
node.next = self.head
self.head = node
return
elif index >= self.get_length():
self.tail.next = ListNode(val)
self.tail = self.tail.next
return
node = ListNode(val)
cur = self.head
pre = None
while index:
pre = cur
cur = cur.next
index -= 1
node.next = pre.next
pre.next = node
def deleteAtIndex(self, index):
"""
:type index: int
:rtype: None
"""
if index < 0 or index >= self.get_length():
return
if index == 0:
self.head = self.head.next
return
pre = self.head
while index > 1:
pre = pre.next
index -= 1
pre.next = pre.next.next
def deleteAtValue(self, value):
"""
:type index: int
:rtype: None
"""
if self.head.val == value:
self.head = self.head.next
return
cur = self.head
while cur.next:
if cur.next.val == value:
break
cur = cur.next
else:
return
cur.next = cur.next.next
def __iter__(self):
return self.LinkListIterator(self.head)
def __repr__(self):
return "<<" + ",".join(map(str, self)) + ">>"
li = LinkedList([1, 2, 3, 5, 6, 3])
li.show()
print(li.get_length())
print(li.get_index(6))
li.addAtIndex(7, 4)
li.show()
li.deleteAtValue(3)
li.show()
print(li.get_index(4))
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
class MyLinkedList(object):
def __init__(self):
self.head = ListNode()
self.size = 0 # 设置一个链表长度的属性,便于后续操作,注意每次增和删的时候都要更新
def get(self, index):
"""
:type index: int
:rtype: int
"""
if index < 0 or index >= self.size:
return -1
cur = self.head.next
while (index):
cur = cur.next
index -= 1
return cur.val
def addAtHead(self, val):
"""
:type val: int
:rtype: None
"""
new_node = ListNode(val)
new_node.next = self.head.next
self.head.next = new_node
self.size += 1
def addAtTail(self, val):
"""
:type val: int
:rtype: None
"""
new_node = ListNode(val)
cur = self.head
while (cur.next):
cur = cur.next
cur.next = new_node
self.size += 1
def addAtIndex(self, index, val):
"""
:type index: int
:type val: int
:rtype: None
"""
if index < 0:
self.addAtHead(val)
return
elif index == self.size:
self.addAtTail(val)
return
elif index > self.size:
return
node = ListNode(val)
pre = self.head
while (index):
pre = pre.next
index -= 1
node.next = pre.next
pre.next = node
self.size += 1
def deleteAtIndex(self, index):
"""
:type index: int
:rtype: None
"""
if index < 0 or index >= self.size:
return
pre = self.head
while (index):
pre = pre.next
index -= 1
pre.next = pre.next.next
self.size -= 1
双链表
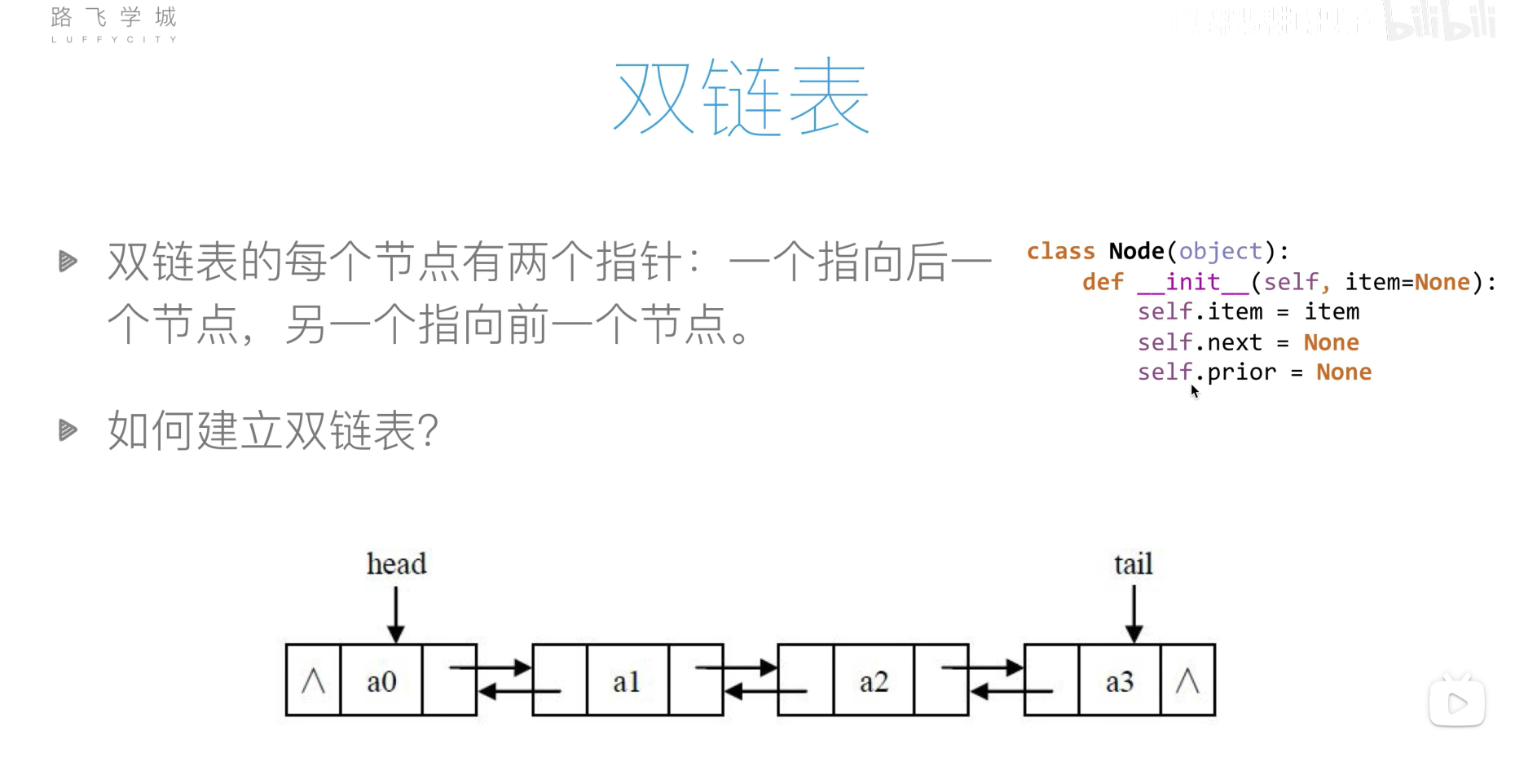
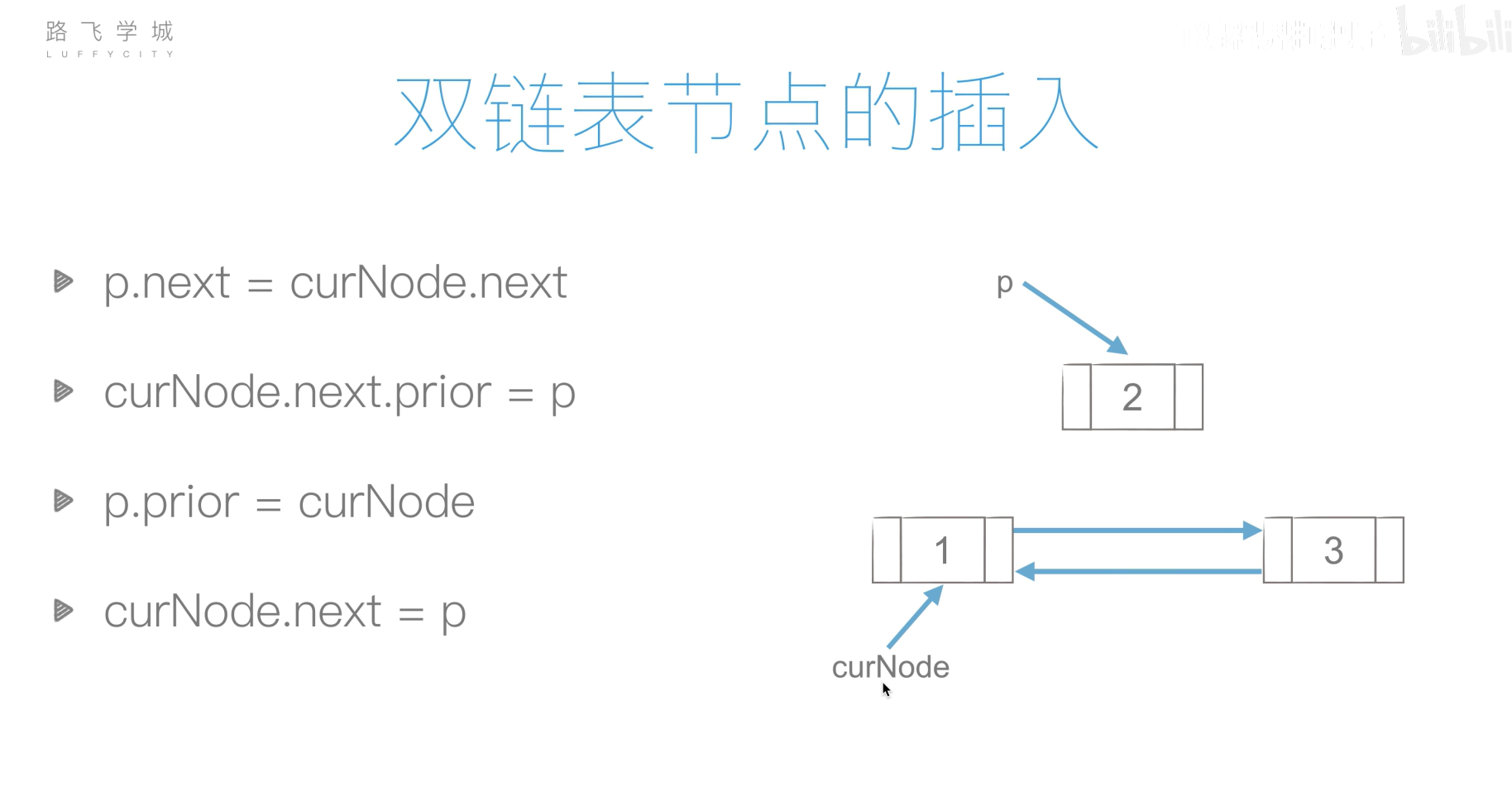
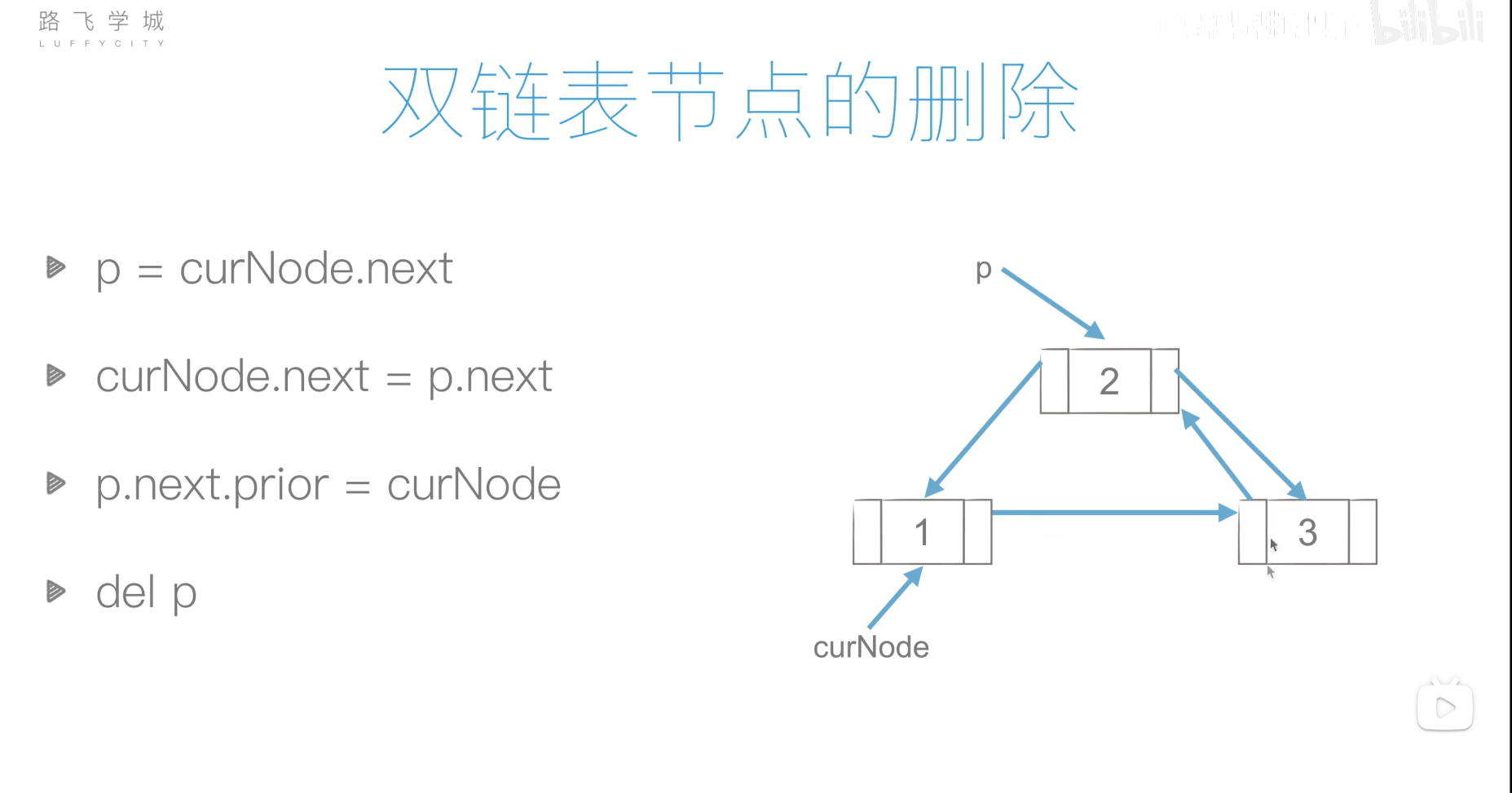
双链表的创建
class Node:
def __init__(self, val):
self.val = val
self.prev = None
self.next = None
class MyLinkedListDouble:
def __init__(self):
self._head, self._tail = Node(0), Node(0) # 虚拟节点
self._head.next, self._tail.prev = self._tail, self._head
self._count = 0 # 添加的节点数
def _get_node(self, index: int) -> Node:
# 当index小于_count//2时, 使用_head查找更快, 反之_tail更快
if index >= self._count // 2:
# 使用prev往前找
node = self._tail
for _ in range(self._count - index):
node = node.prev
else:
# 使用next往后找
node = self._head
for _ in range(index + 1):
node = node.next
return node
def get(self, index: int) -> int:
"""
Get the value of the index-th node in the linked list. If the index is invalid, return -1.
"""
if 0 <= index < self._count:
node = self._get_node(index)
return node.val
else:
return -1
def addAtHead(self, val: int) -> None:
"""
Add a node of value val before the first element of the linked list.
After the insertion, the new node will be the first node of the linked list.
"""
self._update(self._head, self._head.next, val)
def addAtTail(self, val: int) -> None:
"""
Append a node of value val to the last element of the linked list.
"""
self._update(self._tail.prev, self._tail, val)
def addAtIndex(self, index: int, val: int) -> None:
"""
Add a node of value val before the index-th node in the linked list.
If index equals to the length of linked list, the node will be appended to the end of linked list.
If index is greater than the length, the node will not be inserted.
"""
if index < 0:
index = 0
elif index > self._count:
return
node = self._get_node(index)
self._update(node.prev, node, val)
def _update(self, prev: Node, next: Node, val: int) -> None:
"""
更新节点
:param prev: 相对于更新的前一个节点
:param next: 相对于更新的后一个节点
:param val: 要添加的节点值
"""
# 计数累加
self._count += 1
node = Node(val)
prev.next, next.prev = node, node
node.prev, node.next = prev, next
def deleteAtIndex(self, index: int) -> None:
"""
Delete the index-th node in the linked list, if the index is valid.
"""
if 0 <= index < self._count:
node = self._get_node(index)
# 计数-1
self._count -= 1
node.prev.next, node.next.prev = node.next, node.prev
链表与数组的差别
- 链表
- 优点:插入删除操作较快,内存可以动态分配
- 缺点:查找操作较慢
- 数组
- 优点:结构简单,查找操作快
- 缺点:插入删除操作较慢,内存不能动态分配
哈希表
python中的集合,字典结构在底层都是用的哈希表来实现的
哈希表(开辟的一系列连续的地址即数组)
哈希函数(计算输入的值在哈希表中对应下标的函数)
哈希冲突(对于不同的输入哈希函数输出的结果可能相同)
- 解决哈希冲突的方法
- 线性探测法:如果地址冲突,那么它所存放的位置在哈希表中加一
- 二次探测法:利用二次函数,计算冲突时,应该存储的位置
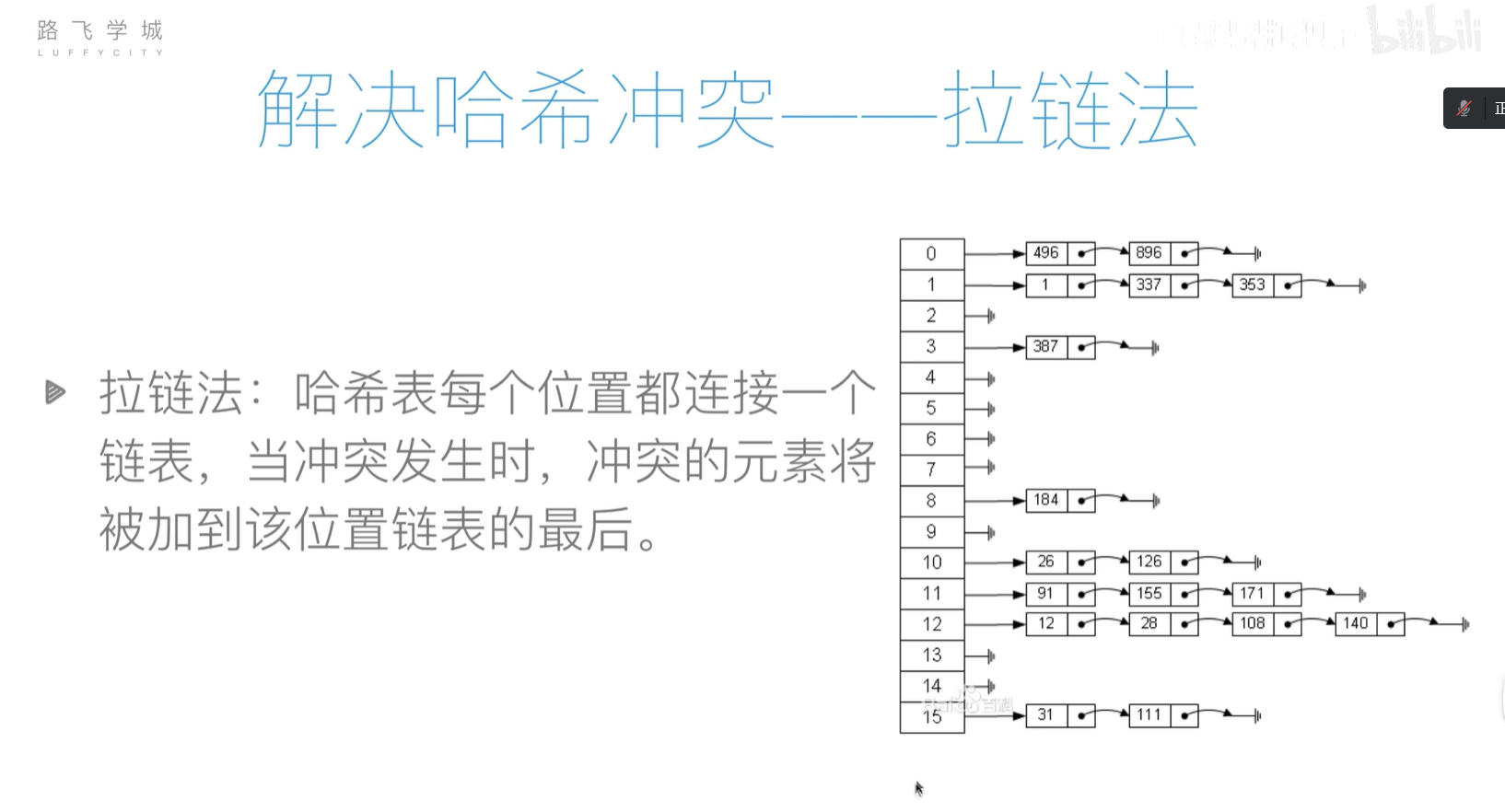
- 拉链存储法:哈希表的每个节点存储的是链表
-
树和二叉树
基本概念
- 根节点
- 叶子节点
- 树的深度
- 节点的度
- 树的度
- 父亲节点
- 孩子节点(左孩子/右孩子)
- 子树
二叉树(度为2的树)
二叉树的性质
-
对于非空二叉树,如果叶子节点树为n0,度为2的节点数为n2,则有n0=n2+1
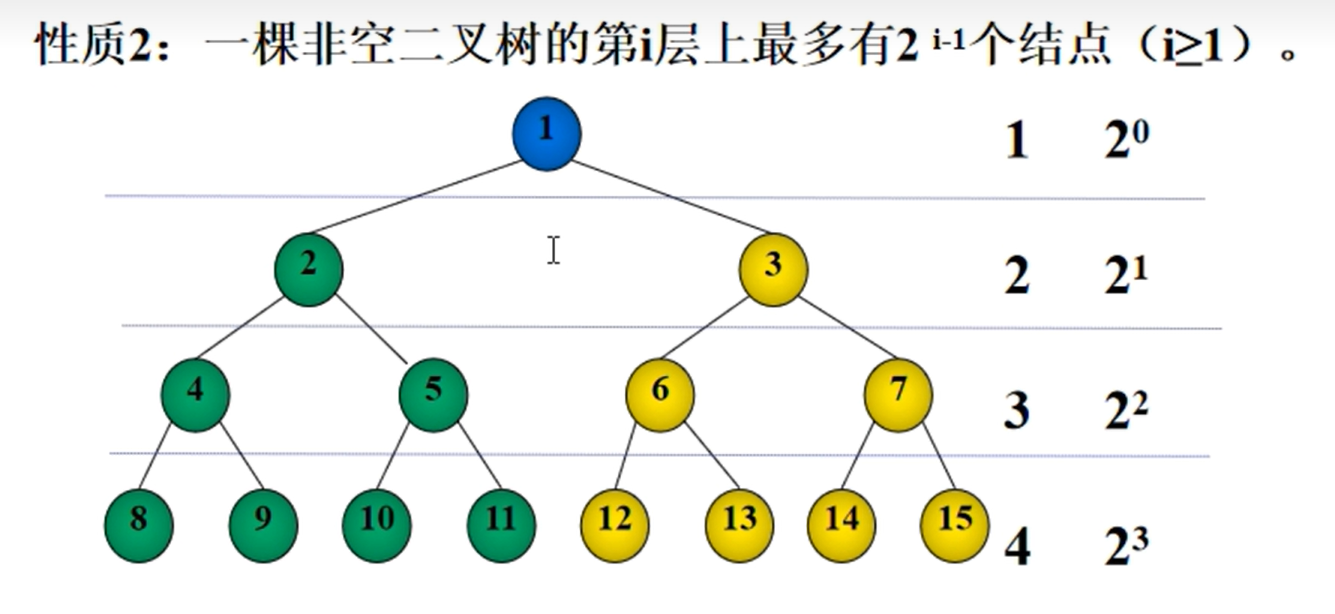
-
对于非空二叉树的第i层上最多有2i-1个节点(满二叉树)
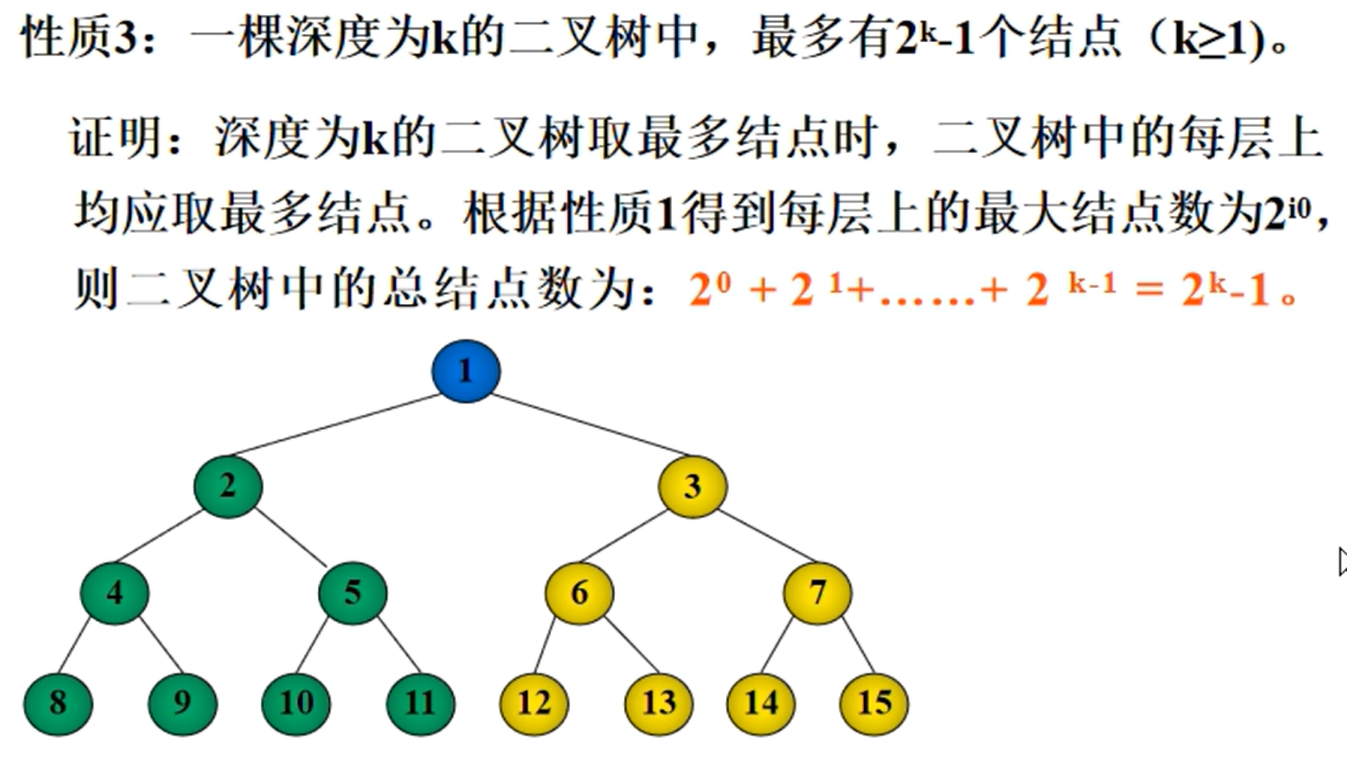
-
一颗深度为k的二叉树中,最多有2k-1个节点(满二叉树)
-
具有n个节点的完全二叉树的深度为:\(\lfloor log_2n \rfloor+1\)
-
如果对于一颗有n个节点的完全二叉树的节点按层序编号,则对任意节点i(1<=i<=n)
-
如果i=1,则节点i时二叉树的根节点,如果i>1,则其父亲节点为\(\lfloor i/2 \rfloor\)
-
如果\(2i\leq n\),则其左孩子是节点2i,否则i无左孩子,为叶子节点
-
如果\(2i+1\leq n\),其右孩子是节点2i+1,否则节点i无右孩子
-

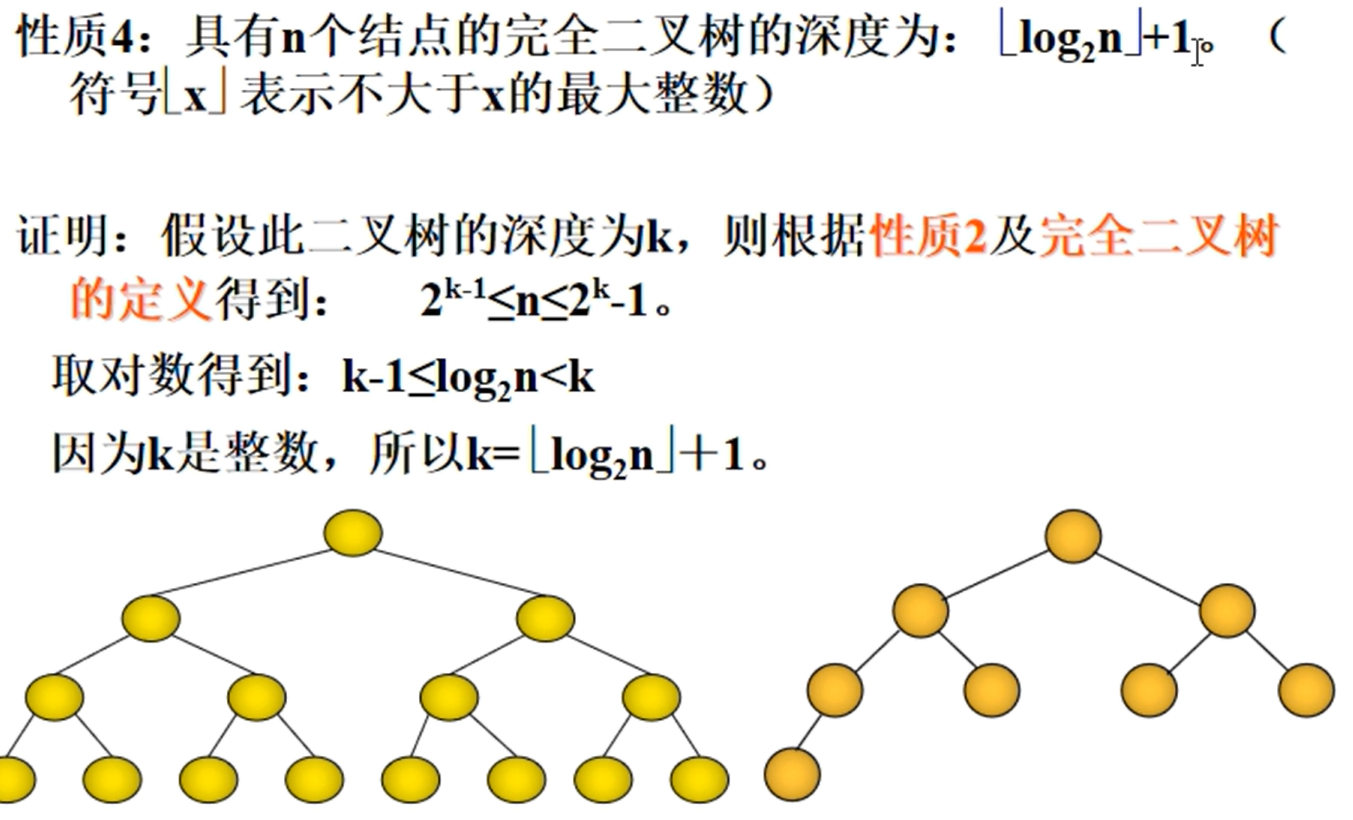
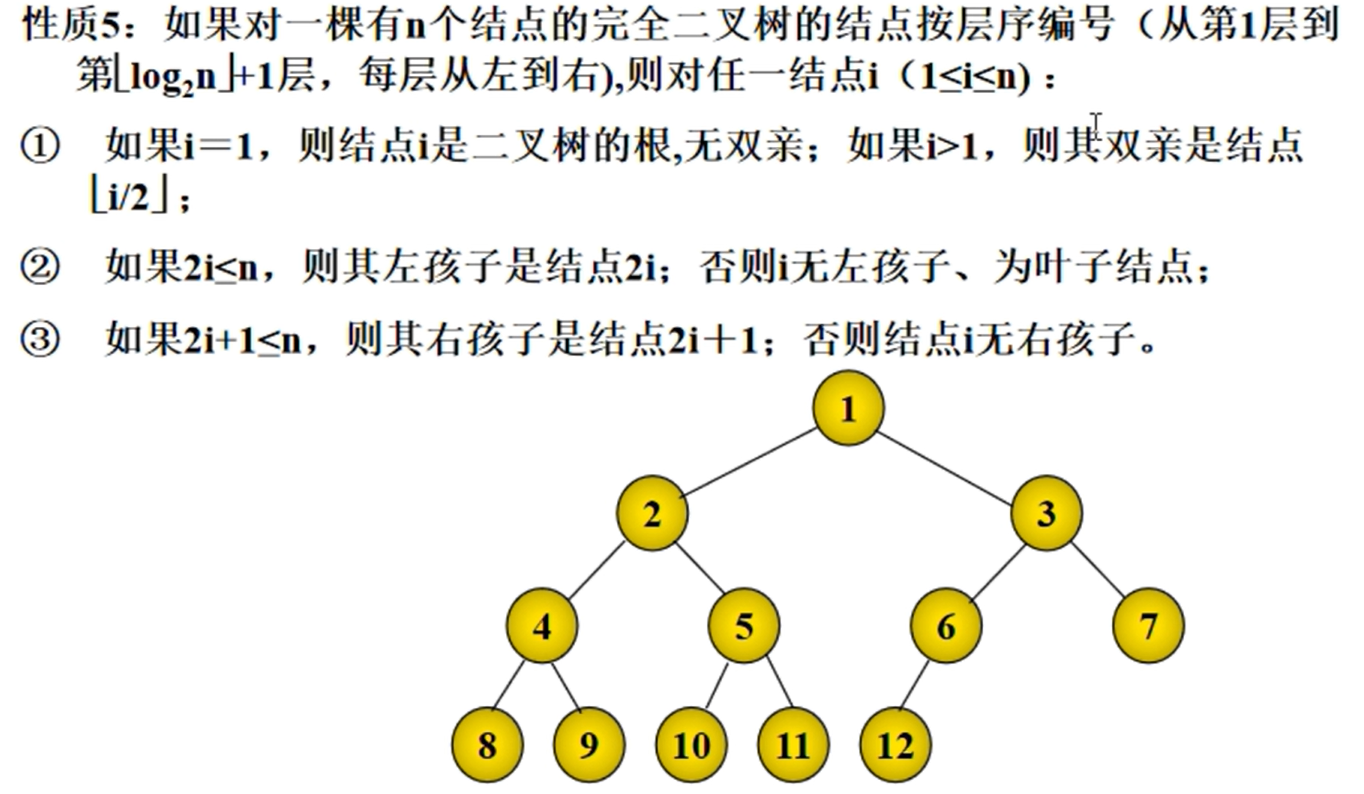
完全二叉树
满二叉树
存储方式
-
顺序存储(用列表或者数组储存)(一般适用于完全二叉树)
-
链式存储
-
列表存储

二叉树的创建
层次按序创建
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Tree(object):
def __init__(self, li=None):
self.root = None
self.lt = []
if li:
self.extend(li)
def extend(self, li: list): # 层次添加创建
for i in li:
self.add(i)
self.clear()
def add(self, number):
# if number is None:
# self.lt.pop(0)
# return
node = TreeNode(number) # 将输入的数字节点化,使其具有左右孩子的属性
if self.root == None:
self.root = node
self.lt.append(self.root)
else:
while self.lt:
point = self.lt[0] # 依次对左右孩子未满的节点分配孩子
if point.val == None:
self.lt.pop(0)
continue
if point.left == None:
point.left = node
self.lt.append(point.left) # 该节点后面作为父节点也是未满的,也要加入到列表中。
return
if point.right == None:
point.right = node
self.lt.append(point.right) # 与左孩子同理
self.lt.pop(0) # 表示该节点已拥有左右孩子,从未满列表中去除
return
def clear(self): # 清除值为None的节点
def level_order_traversal(root: TreeNode):
queue = deque()
queue.append(root)
while len(queue) > 0:
node = queue.popleft()
if node.left and node.left.val == None:
node.left = None
if node.left:
queue.append(node.left)
if node.right and node.right.val == None:
node.right = None
if node.right:
queue.append(node.right)
level_order_traversal(self.root)
def show(self): # 前序遍历输出
def dfs(root):
if not root:
return
print(root.val, end=" ")
dfs(root.left)
dfs(root.right)
dfs(self.root)
def search(self, val):
def searchdata(T, val):
if T == None:
return None
if T.val == val:
return T
else:
p = searchdata(T.left, val)
if p != None:
return p
p = searchdata(T.right, val)
if p != None:
return p
return searchdata(self.root, val)
函数前序创建
def creat_binary_tree(input_list=[]):
# 构建二叉树
# param input_list:输入数列
# 当我们在函数中传入的数列不存在或者传入的数列中元素的个数等于0时,表示是一棵空树
# 此时不需要操作,直接返回None即可
if input_list is None or len(input_list) == 0:
return None
# 结点中的数据等于列表中的第一个元素,每次pop出去一个元素,后面的元素会往前走一个位置
# 这样可以保证元素的一次弹出
val = input_list.pop(0)
# 当弹出的元素是None时,表示该节点为空,直接返回None
if val is None:
return None
# 通过刚才定义的TreeNode类新建node
node = TreeNode(val)
# node的左孩子等于弹出的结点,即input_list.pop(0)弹出的元素
node.left = creat_binary_tree(input_list)
# node的右孩子等于弹出的结点,即input_list.pop(0)弹出的元素
node.right = creat_binary_tree(input_list)
# 返回node结点
return node
二叉树的遍历
- 递归遍历
- 非递归遍历
- 前序遍历
- 中序遍历
- 后序遍历
- 层次遍历
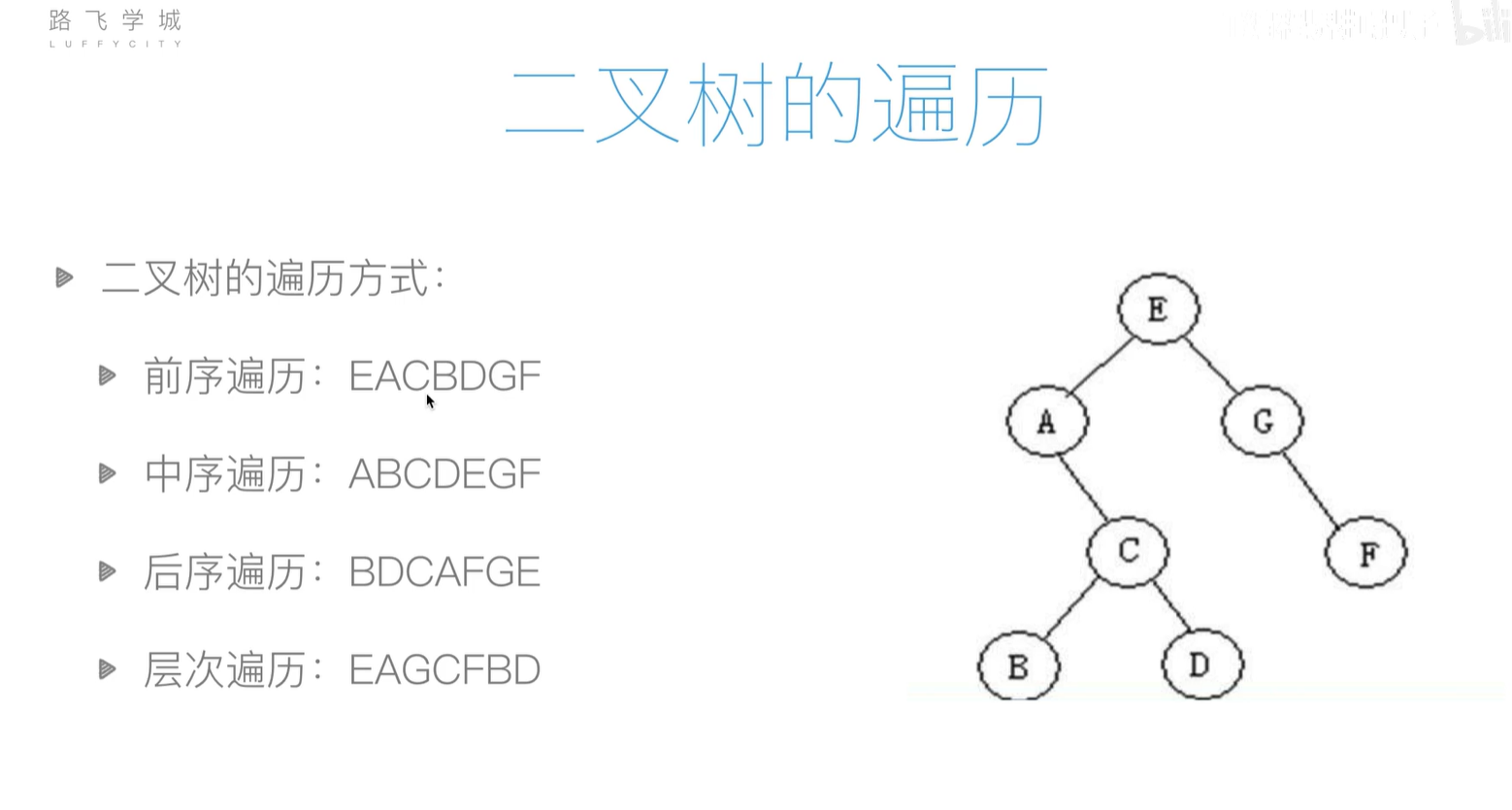
递归遍历代码
def pre_order_traversal(node):
# 前序遍历
# param node:二叉树节点
# 当node为空表示为一棵空树,不需要进行前序遍历直接返回即可
if node is None:
return
# 此时node不为空,直接打印node的val域
print(node.val, end=" ")
# 递归的先序遍历node的左孩子
pre_order_traversal(node.left)
# 递归的先序遍历node的左孩子
pre_order_traversal(node.right)
return node
#
def in_order_traversal(node):
# 中序遍历
# param node:二叉树节点
if node is None:
return
# 递归的中序遍历node的左孩子
in_order_traversal(node.left)
# 打印节点的值
print(node.val, end=" ")
# 递归的中序遍历node的左孩子
in_order_traversal(node.right)
return node
def post_order_traversal(node):
# 后序遍历
# param node:二叉树节点
if node is None:
return
# 递归的后序遍历node的左孩子
post_order_traversal(node.left)
# 递归的后序遍历node的左孩子
post_order_traversal(node.right)
# 打印节点的值
print(node.val, end=" ")
return node
from collections import deque, Counter
def level_order_traversal(root: TreeNode):
queue = deque()
queue.append(root)
while len(queue) > 0:
node = queue.popleft()
print(node.val, end=" ")
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
非递归遍历代码
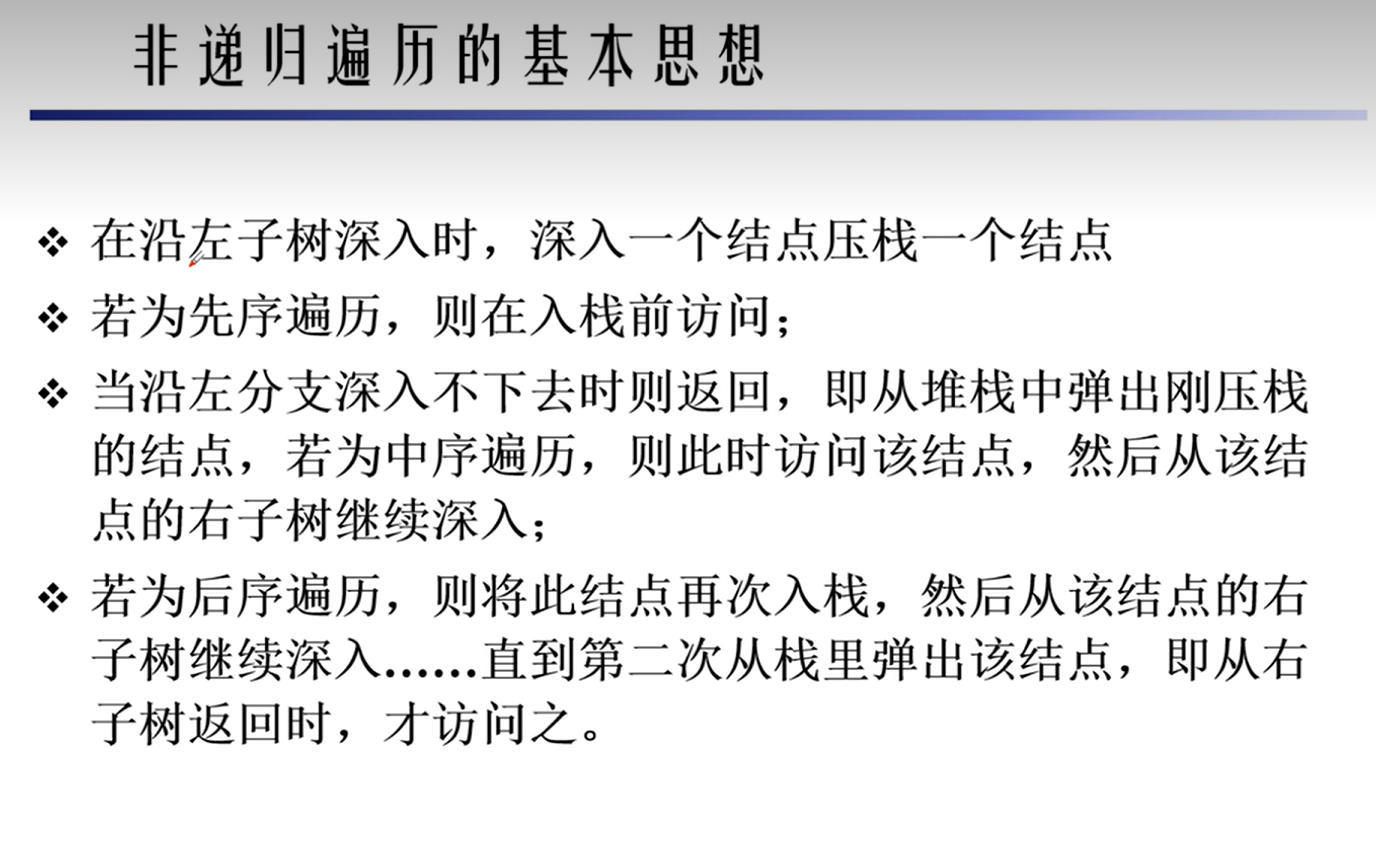
def preorderTraversal(root: TreeNode) -> List[int]:
# 根结点为空则返回空列表
if not root:
return []
stack = [root]
result = []
while stack:
node = stack.pop()
# 中结点先处理
result.append(node.val)
# 右孩子先入栈
if node.right:
stack.append(node.right)
# 左孩子后入栈
if node.left:
stack.append(node.left)
return result
# 中序遍历-迭代-LC94_二叉树的中序遍历
def inorderTraversal(root: TreeNode) -> List[int]:
if not root:
return []
stack = [] # 不能提前将root结点加入stack中
result = []
cur = root
while cur or stack:
# 先迭代访问最底层的左子树结点
if cur:
stack.append(cur)
cur = cur.left
# 到达最左结点后处理栈顶结点
else:
cur = stack.pop()
result.append(cur.val)
# 取栈顶元素右结点
cur = cur.right
return result
# 后序遍历-迭代-LC145_二叉树的后序遍历
def postorderTraversal(root: TreeNode) -> List[int]:
if not root:
return []
stack = [root]
result = []
while stack:
node = stack.pop()
# 中结点先处理
result.append(node.val)
# 左孩子先入栈
if node.left:
stack.append(node.left)
# 右孩子后入栈
if node.right:
stack.append(node.right)
# 将最终的数组翻转
return result[::-1]
哈夫曼树
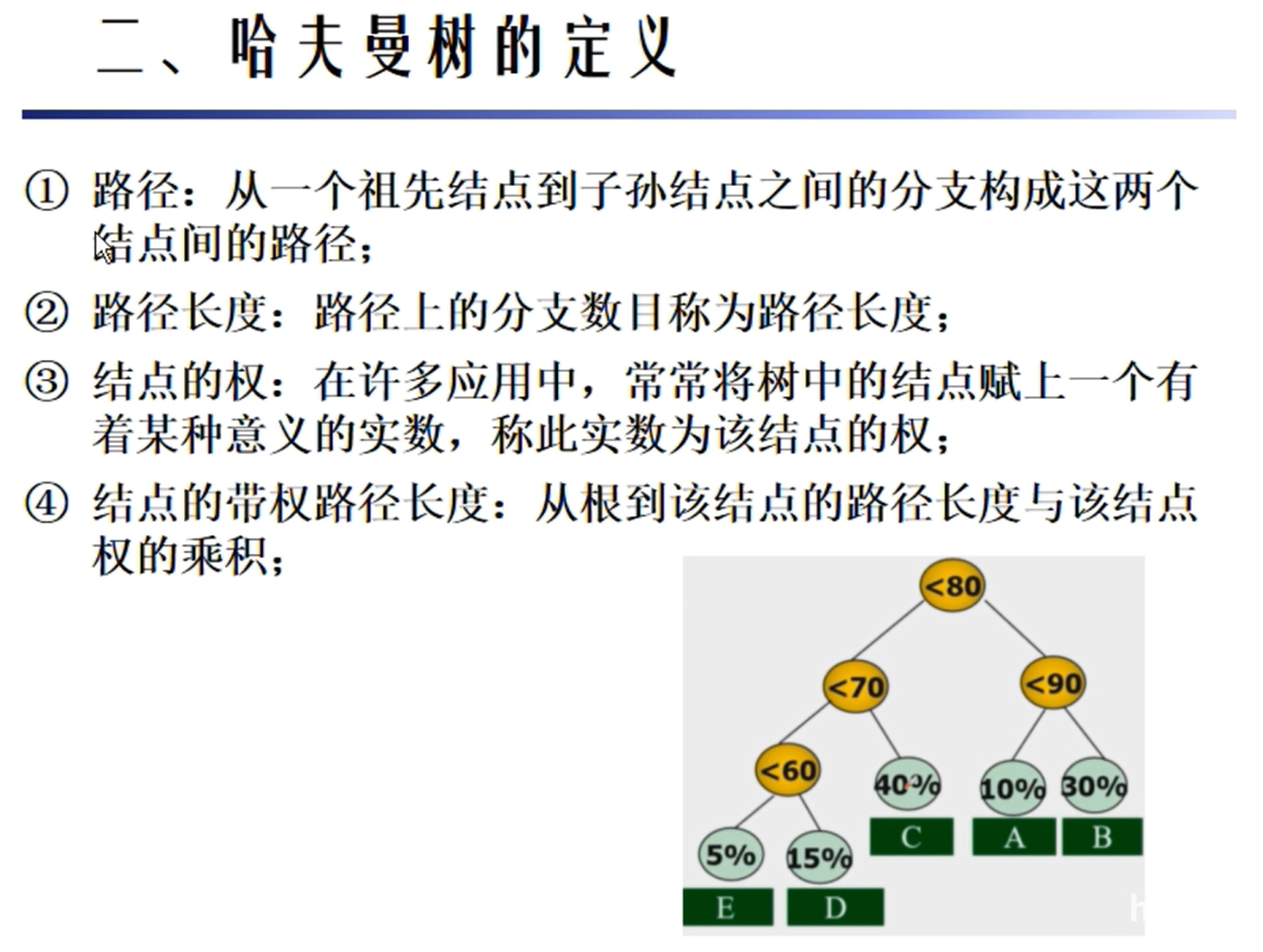
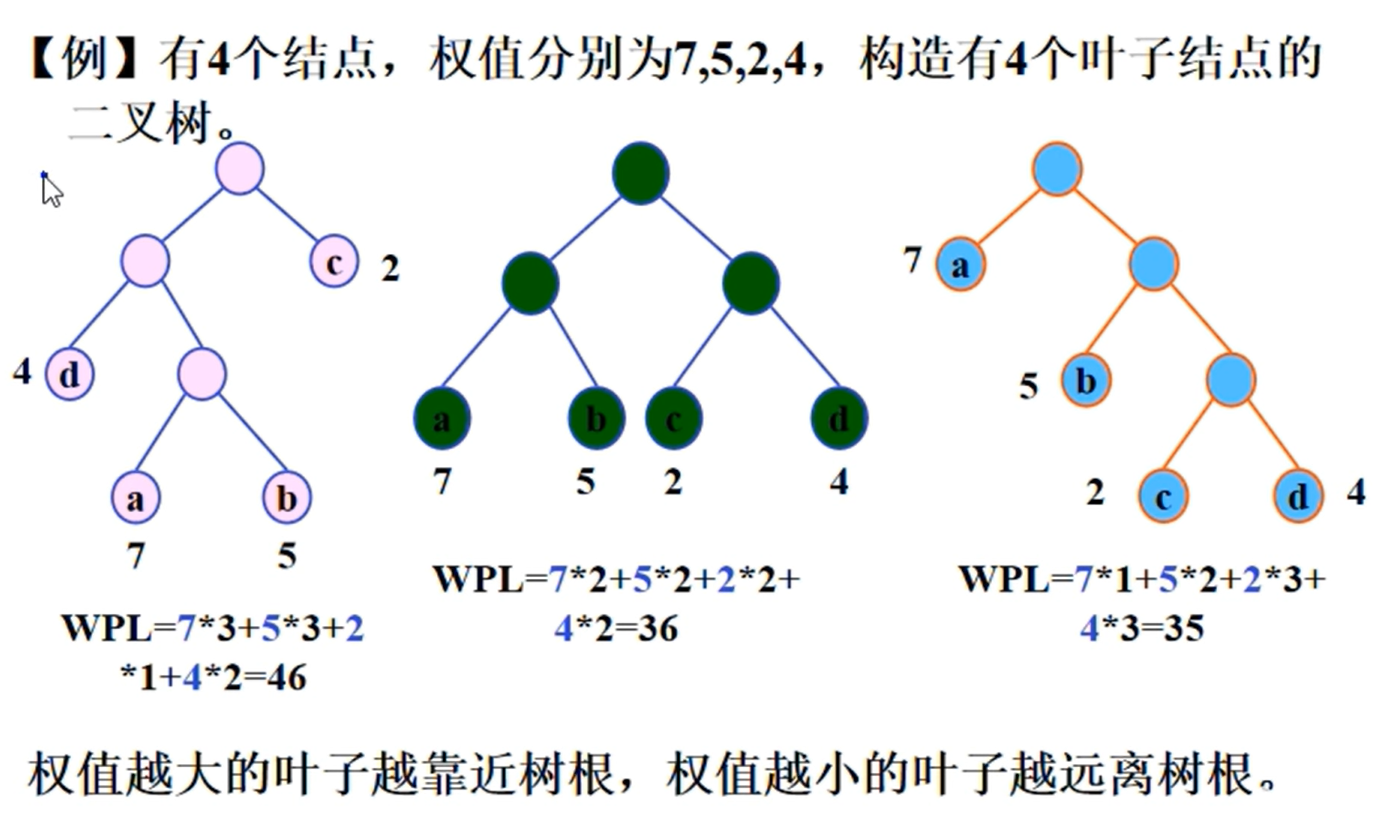

哈夫曼编码
代码
class HuffmanNode:
def __init__(self, val=0):
self.val = val
self.left = None
self.right = None
self.parent = None
class HuffmanTree:
def __init__(self, head=None):
self.head = head
self.lst = []
self.huffman_code = None
def create(self, li: list):
res = []
for i in li:
res.append(HuffmanNode(i))
self.lst = res[:]
while len(res) > 1:
res.sort(key=lambda item: item.val)
node_left = res.pop(0)
node_right = res.pop(0)
node_father = HuffmanNode(node_left.val + node_right.val)
node_father.left = node_left
node_father.right = node_right
node_left.parent = node_father
node_right.parent = node_father
res.append(node_father)
res[0].parent = None
self.head = res[0]
def encoding(self):
if self.head is None:
return
huffman_code = [''] * len(self.lst)
for i in range(len(self.lst)):
node = self.lst[i]
while node != self.head:
if node.parent.left == node:
huffman_code[i] = "0" + huffman_code[i]
else:
huffman_code[i] = "1" + huffman_code[i]
node = node.parent
self.huffman_code = huffman_code
huffmantree = HuffmanTree()
huffmantree.create([2, 4, 5, 7])
level_order_traversal(huffmantree.head)
huffmantree.encoding()
print(huffmantree.huffman_code)
二叉搜索树
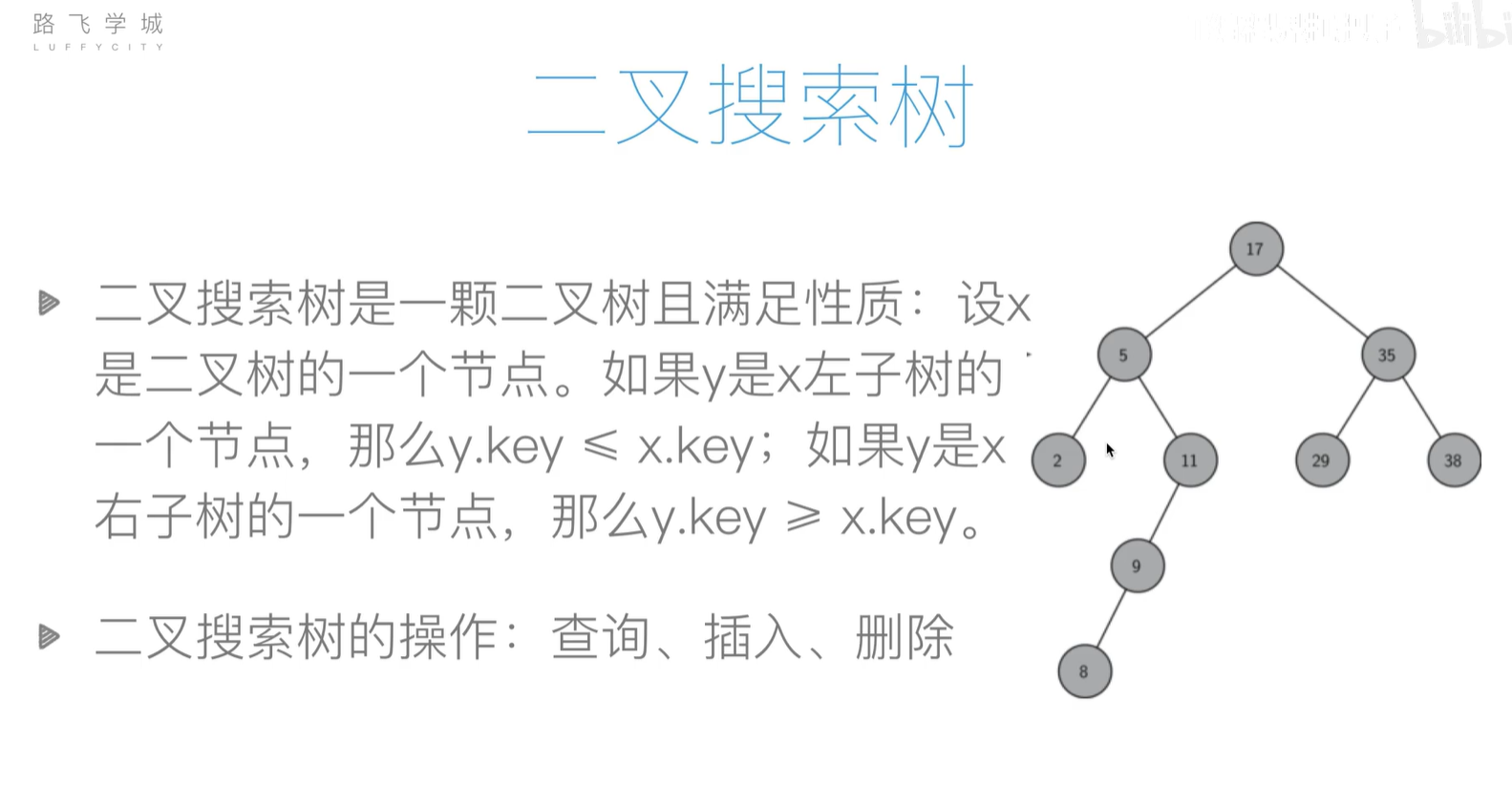
基本操作
- 插入
- 查询
- 删除
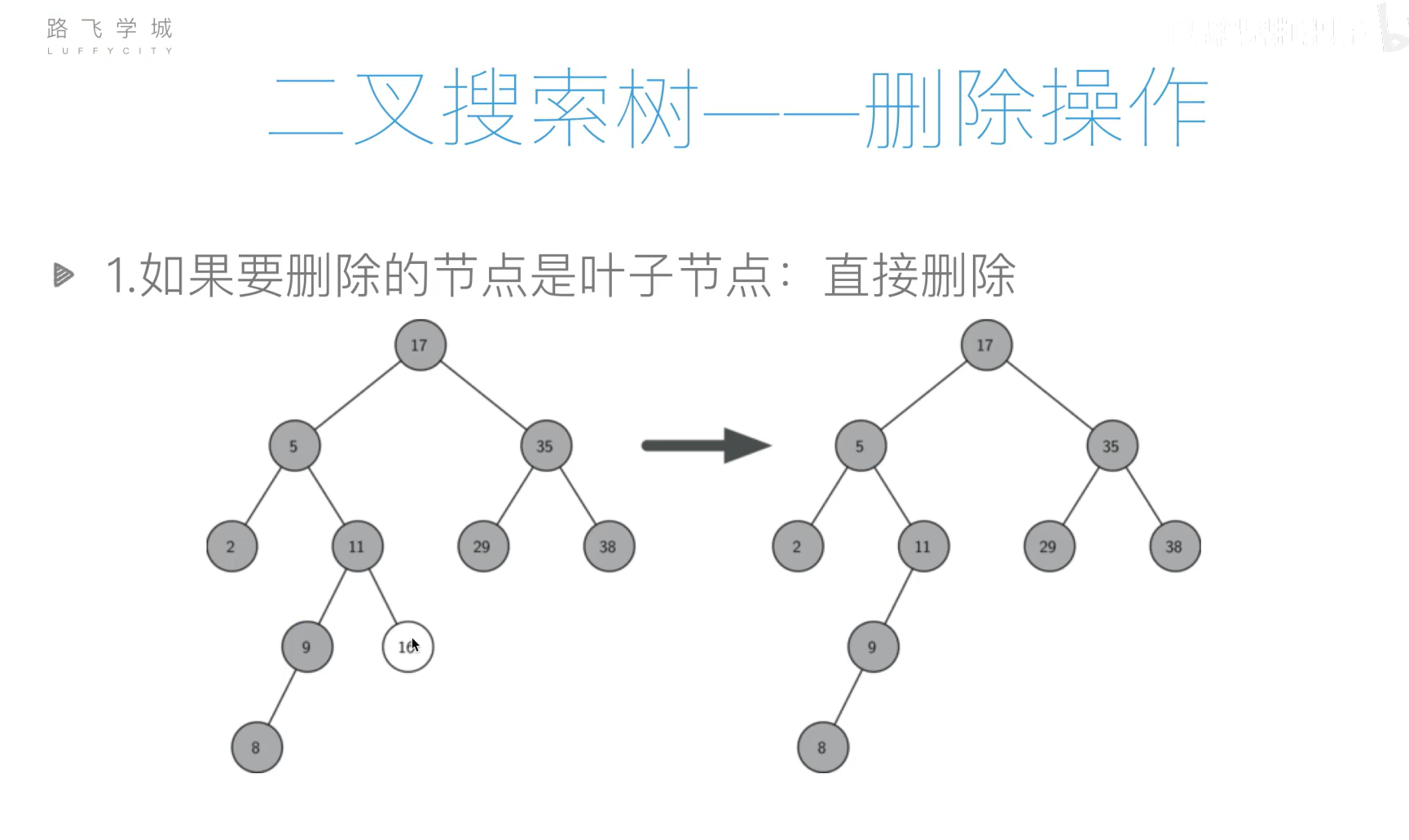
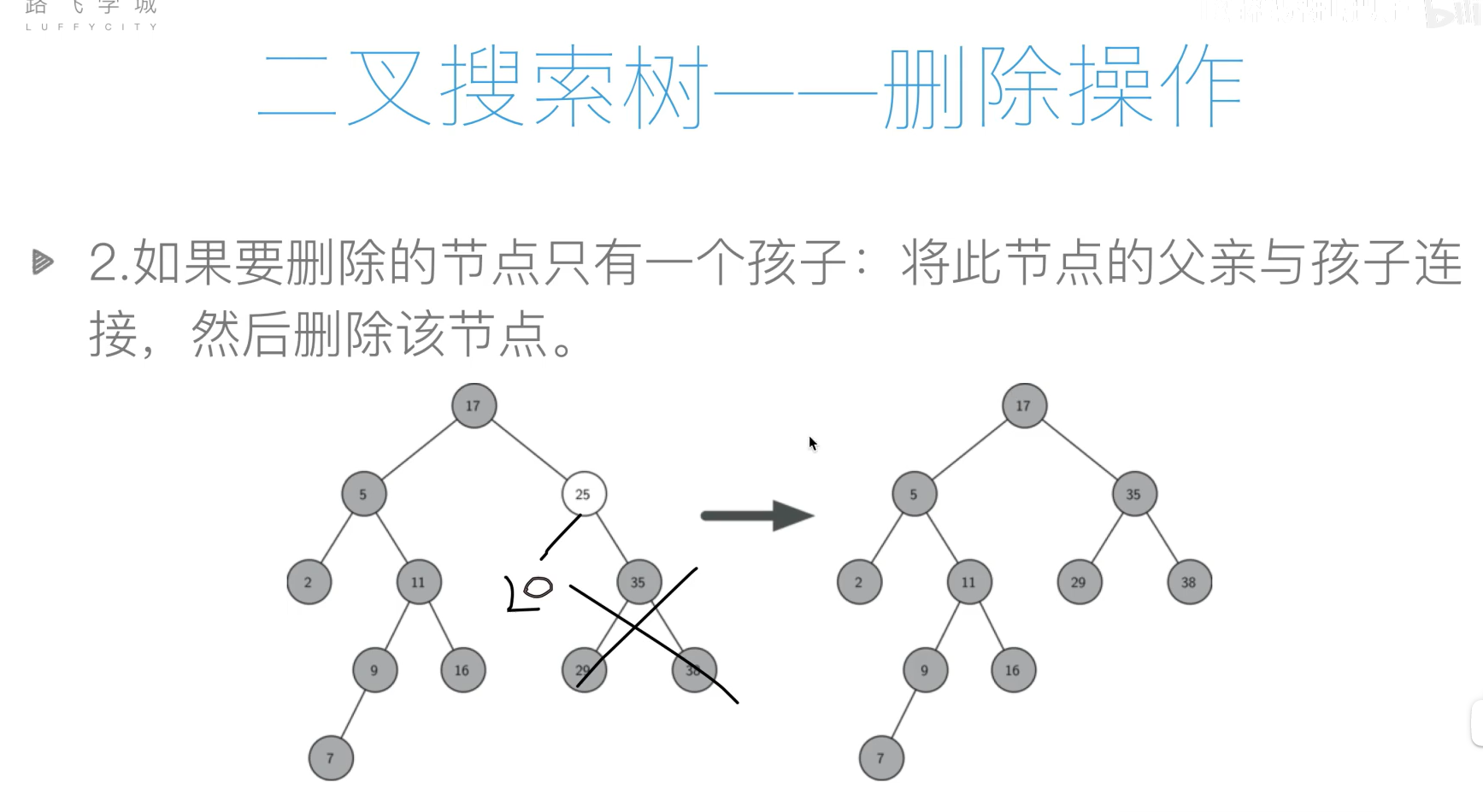
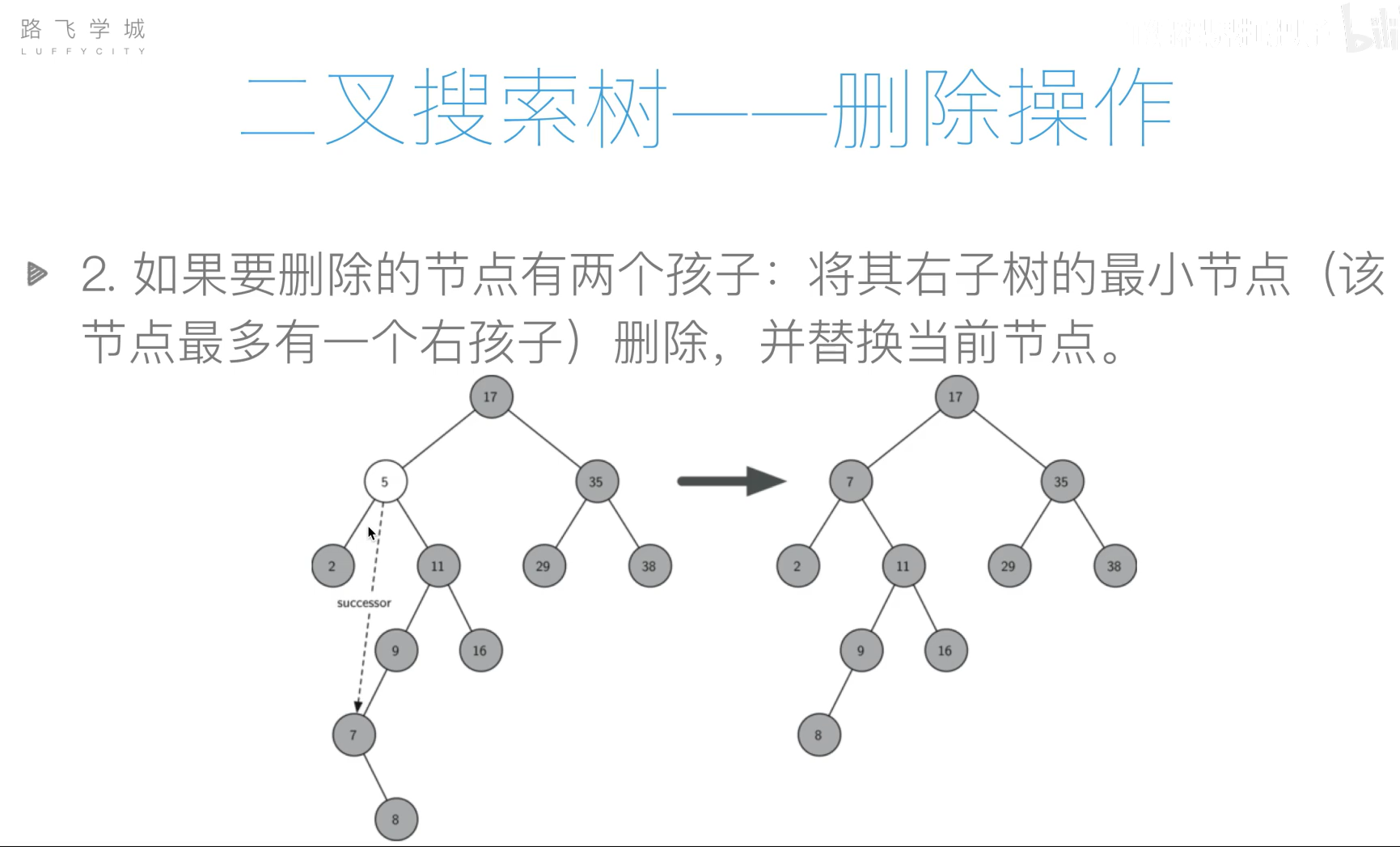
代码
class BiTreeNode:
def __init__(self, data):
self.val = data
self.left = None
self.right = None
self.parent = None
class BST:
def __init__(self, data: list):
self.root = None
if data:
# if self.root is None:
# self.root=BiTreeNode(data[0])
# data=data[1:]
# for i in data:
# self.insert(self.root, i)
for i in data:
self.insert_no_rec(i)
def insert(self, node, val):
if not node:
node = BiTreeNode(val)
elif val <= node.val:
node.left = self.insert(node.left, val)
elif val > node.val:
node.right = self.insert(node.right, val)
return node
def insert_no_rec(self, val):
p = self.root
if not p:
self.root = BiTreeNode(val)
return
while True:
if val <= p.val:
if p.left:
p = p.left
else:
p.left = BiTreeNode(val)
p.left.parent = p
return
elif val > p.val:
if p.right:
p = p.right
else:
p.right = BiTreeNode(val)
p.right.parent = p
return
def query(self, node, val):
if not node:
return None
if node.val < val:
return self.query(node.right, val)
elif node.val > val:
return self.query(node.left, val)
else:
return node
def query_no_rec(self, val):
p = self.root
while p:
if p.val < val:
p = p.right
elif p.val > val:
p = p.left
else:
return p
return None
def __remove_node_1(self, node):
if not node.parent:
self.root = None
if node == node.parent.left:
node.parent.left = None
else:
node.parent.right = None
def __remove_node_21(self, node):
if not node.parent:
self.root = node.left
node.left.parent = None
elif node == node.parent.left:
node.parent.left = node.left
node.left.parent = node.parent
else:
node.parent.right = node.left
node.left.parent = node.parent
def __remove_node_22(self, node):
if not node.parent:
self.root = node.right
elif node == node.parent.left:
node.parent.left = node.right
node.right.parent = node.parent
else:
node.parent.right = node.right
node.right.parent = node.parent
def delete(self, val):
if self.root:
node = self.query_no_rec(val)
if not node:
return False
if not node.left and not node.right:
self.__remove_node_1(node)
elif not node.right:
self.__remove_node_21(node)
elif not node.left:
self.__remove_node_22(node)
else:
min_node = node.right
while min_node.left:
min_node = min_node.left
node.val = min_node.val
if min_node.right:
self.__remove_node_22(min_node)
else:
self.__remove_node_1(min_node)
T = BST([5, 1, 2, 3, 4, 1, 6, 2])
in_order_traversal(T.root)
T.delete(1)
T.delete(1)
T.delete(6)
print()
in_order_traversal(T.root)
AVL树(平衡二叉搜索树)

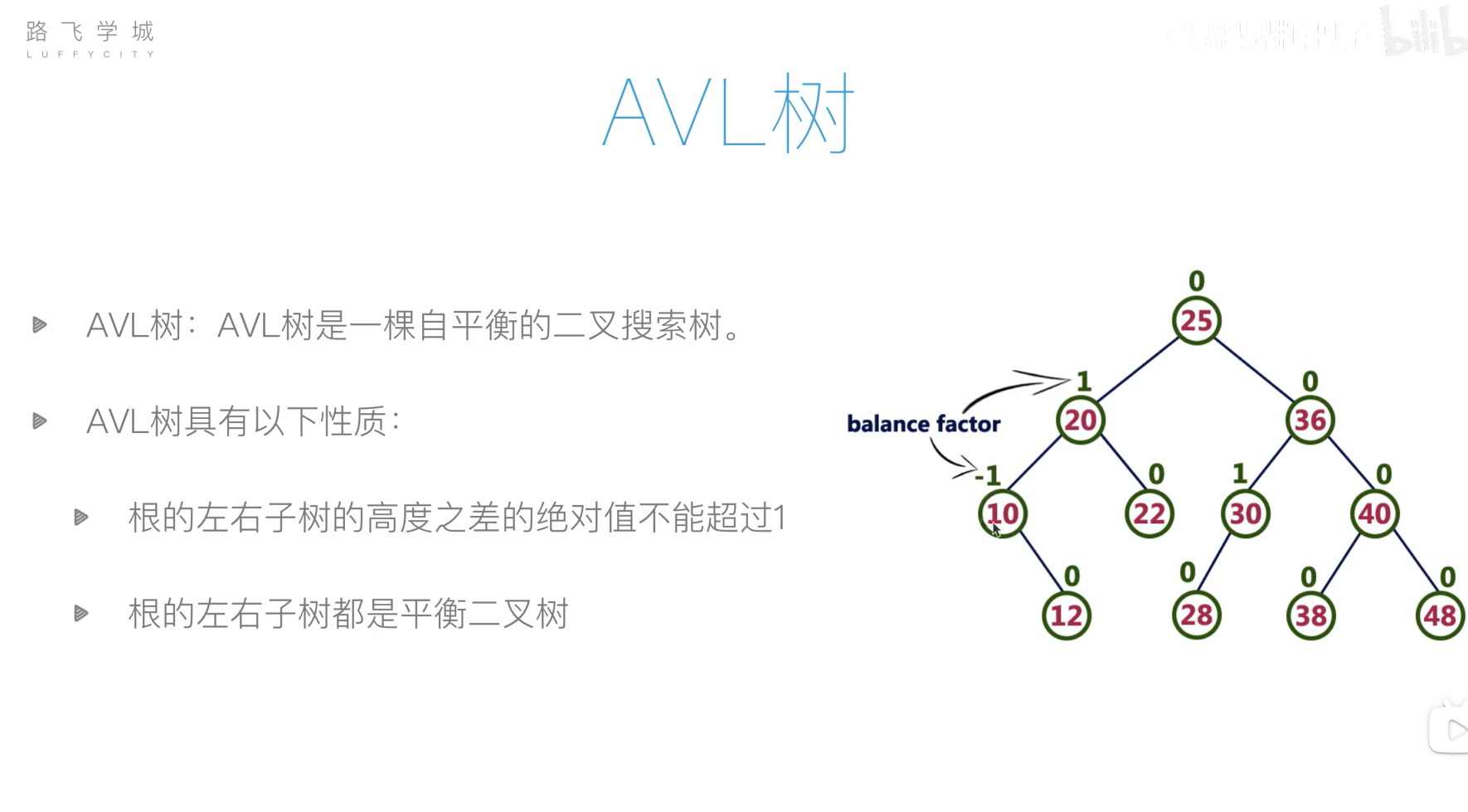

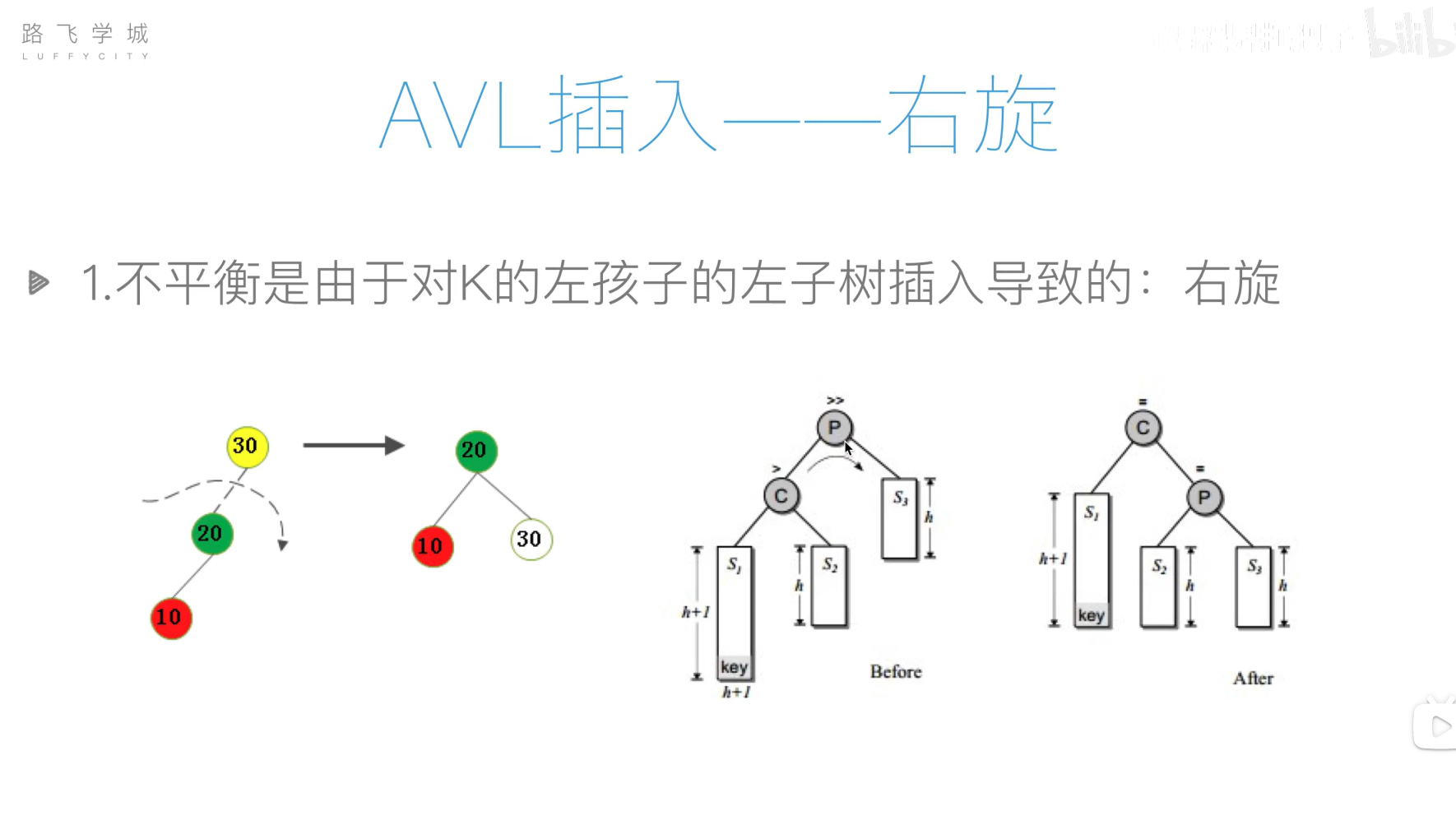
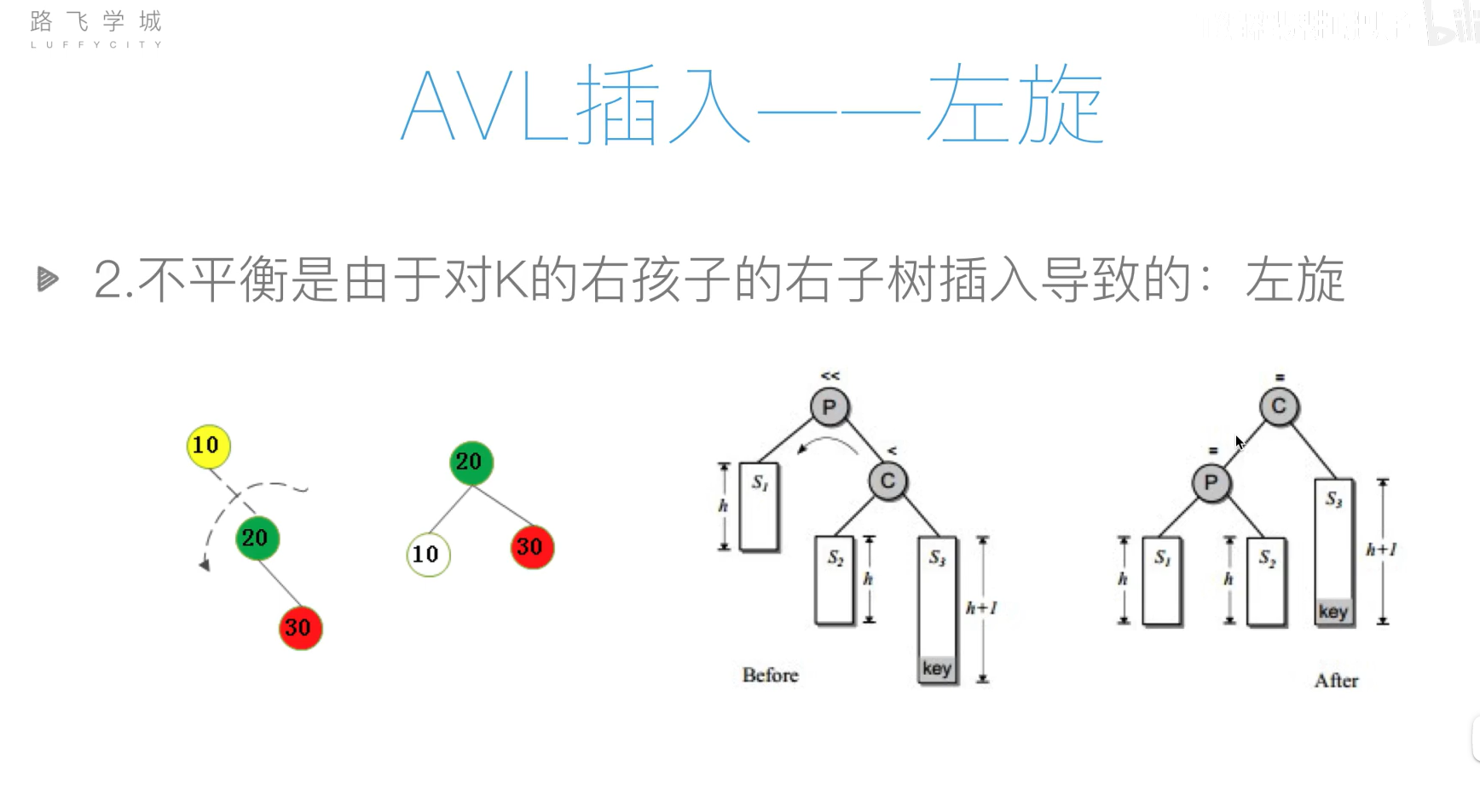
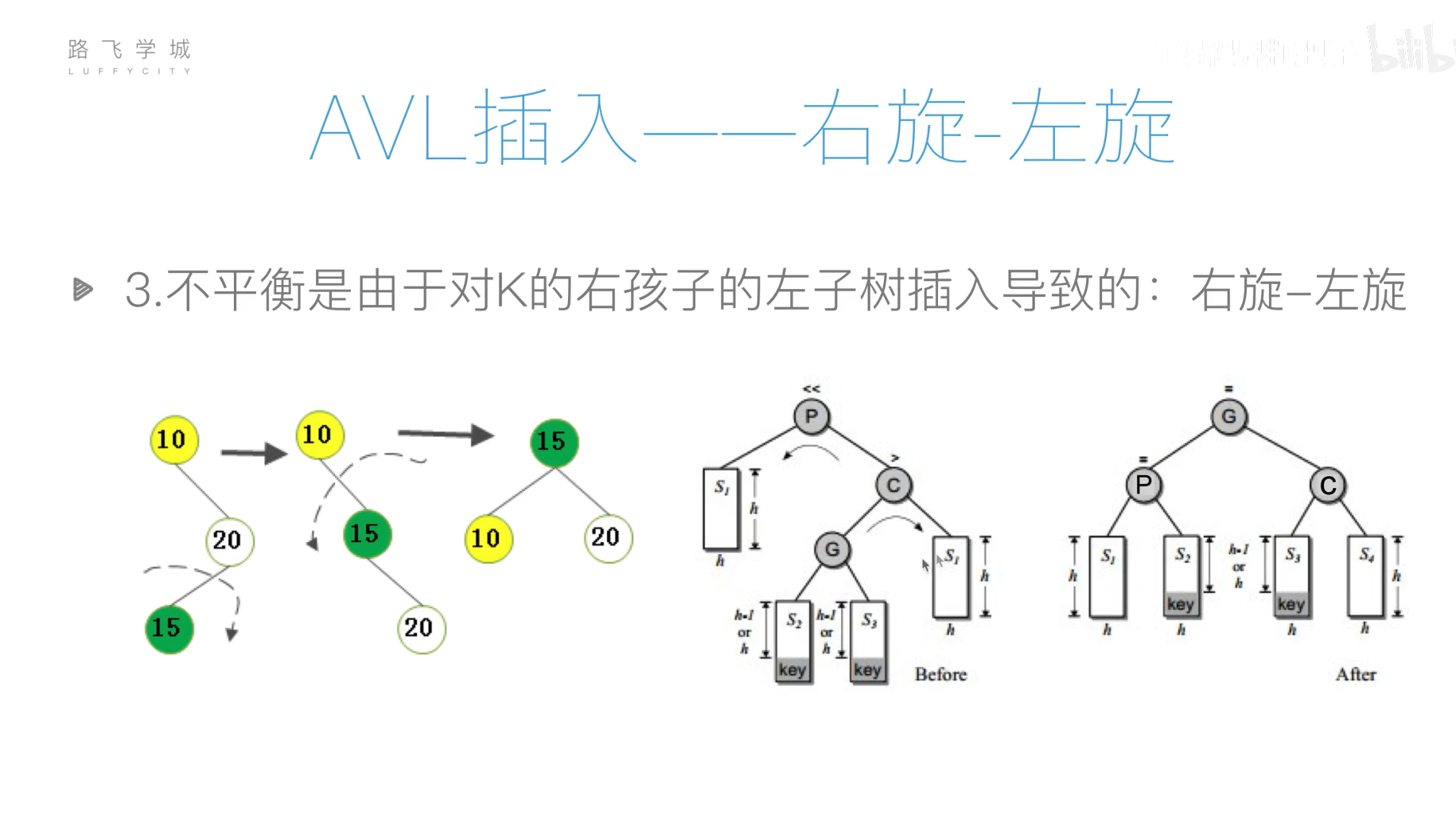
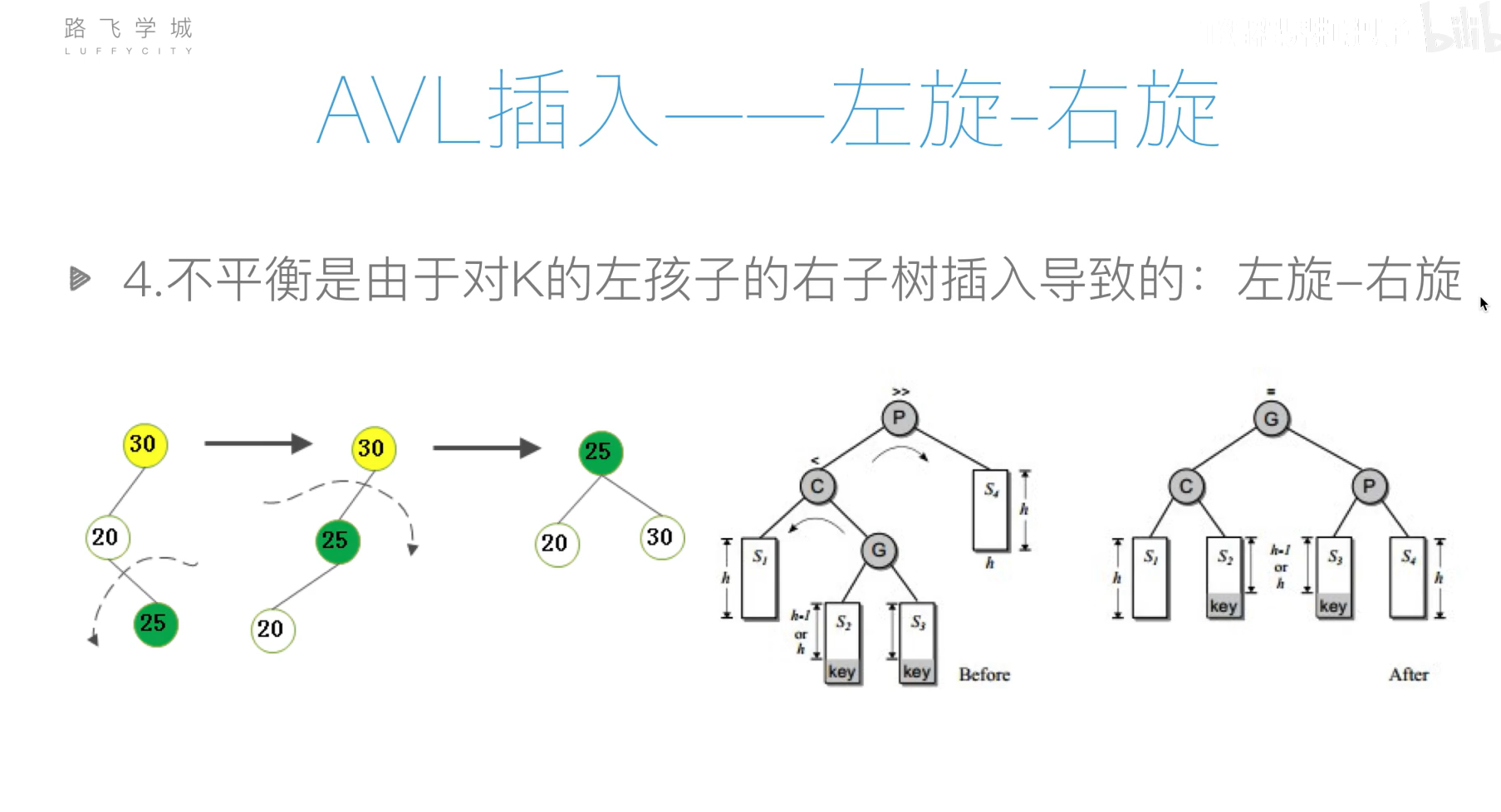
旋转操作过于复杂,可以先将列表元素排好序,然后使用二分递归的方法
代码如下:
二分递归代码
def sortedArrayToBST(nums: list[int]) -> TreeNode:
def helper(left, right):
if left > right:
return None
mid = (left + right) // 2
root = TreeNode(nums[mid])
root.left = helper(left, mid - 1)
root.right = helper(mid + 1, right)
return root
return helper(0, len(nums) - 1)
li = [1, 2, 3, 4, 5, 6, 7, 8, 9]
root = sortedArrayToBST(li)
in_order_traversal(root)
print()
pre_order_traversal(root)
树和森林
基本概念
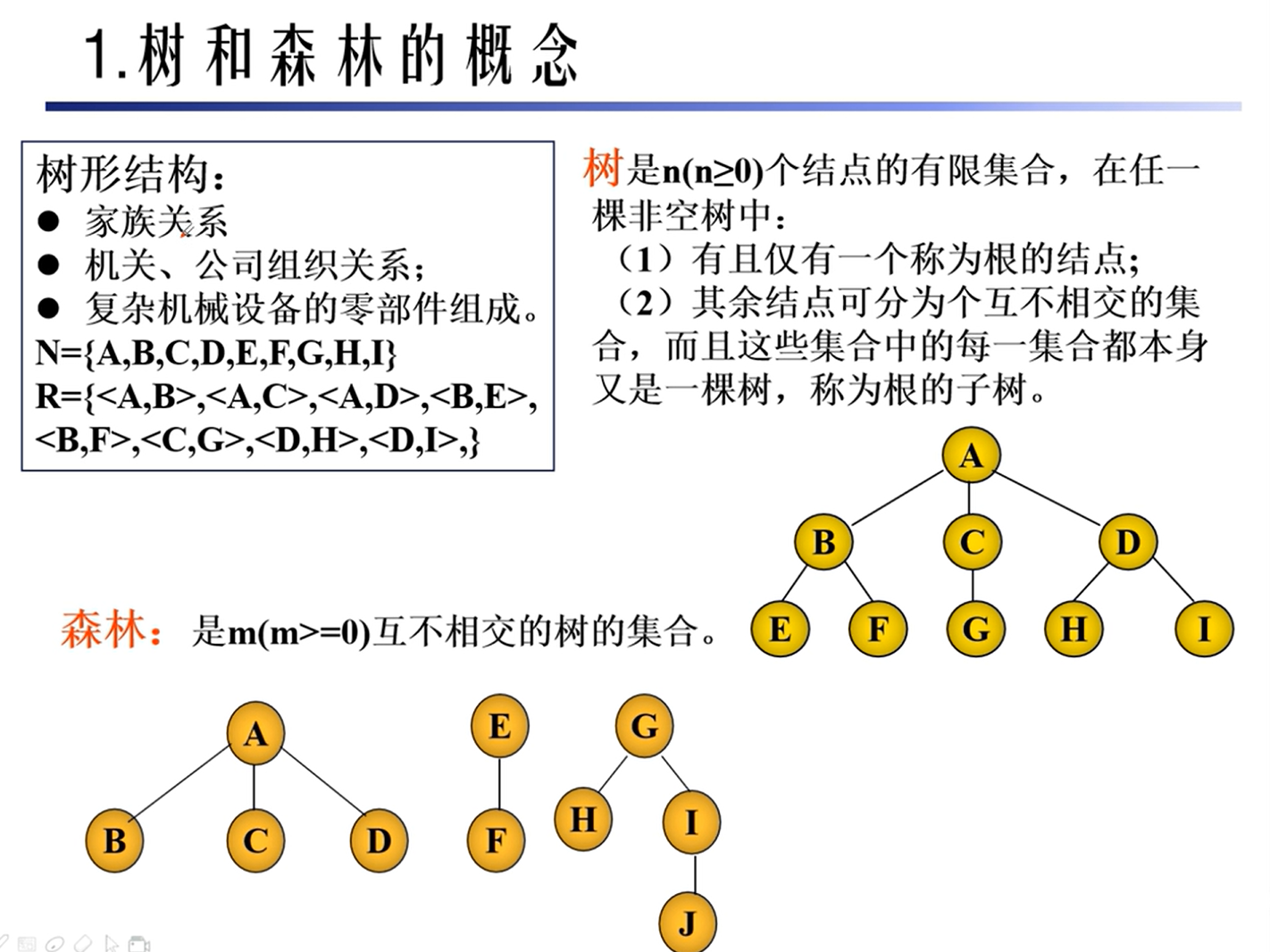
性质
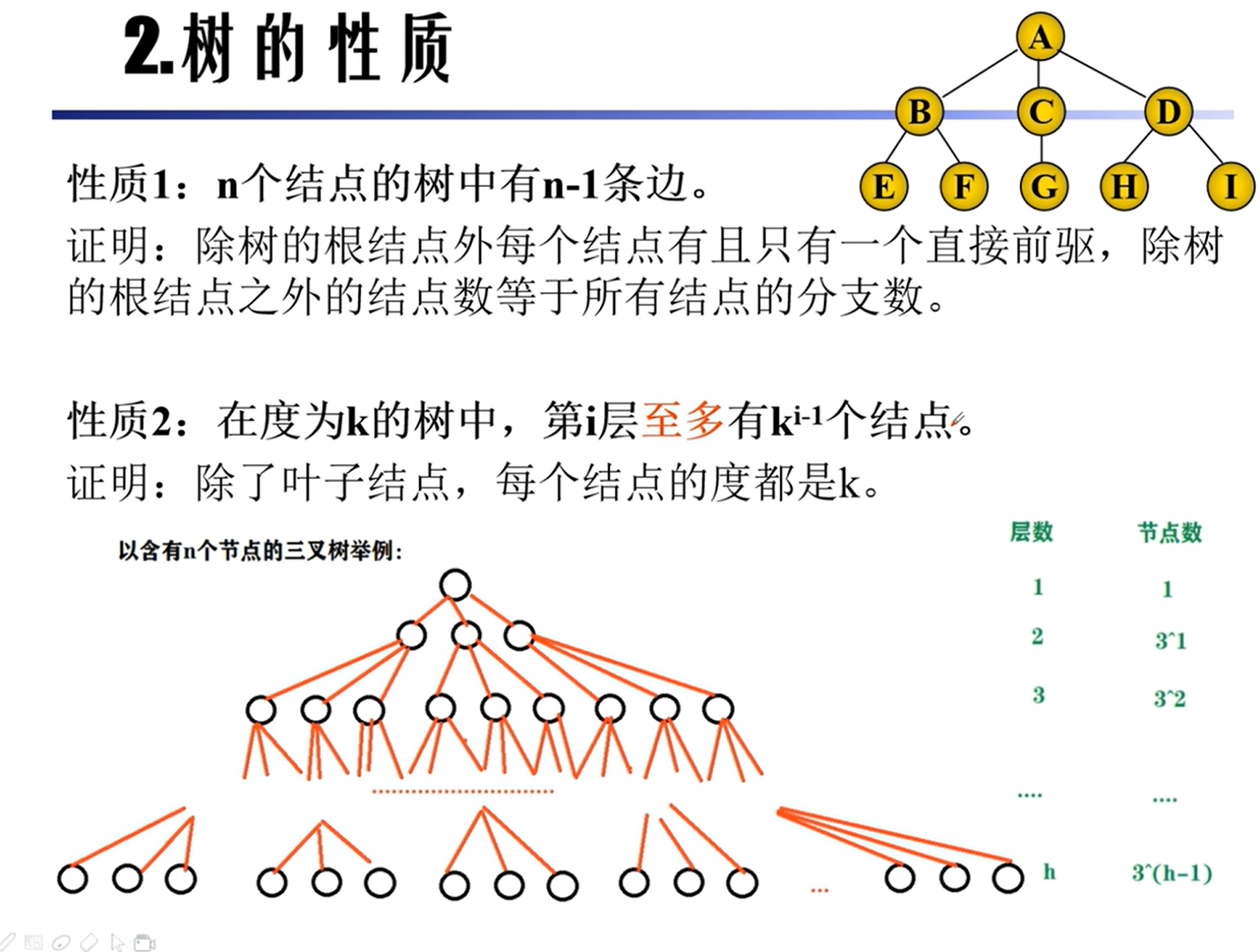
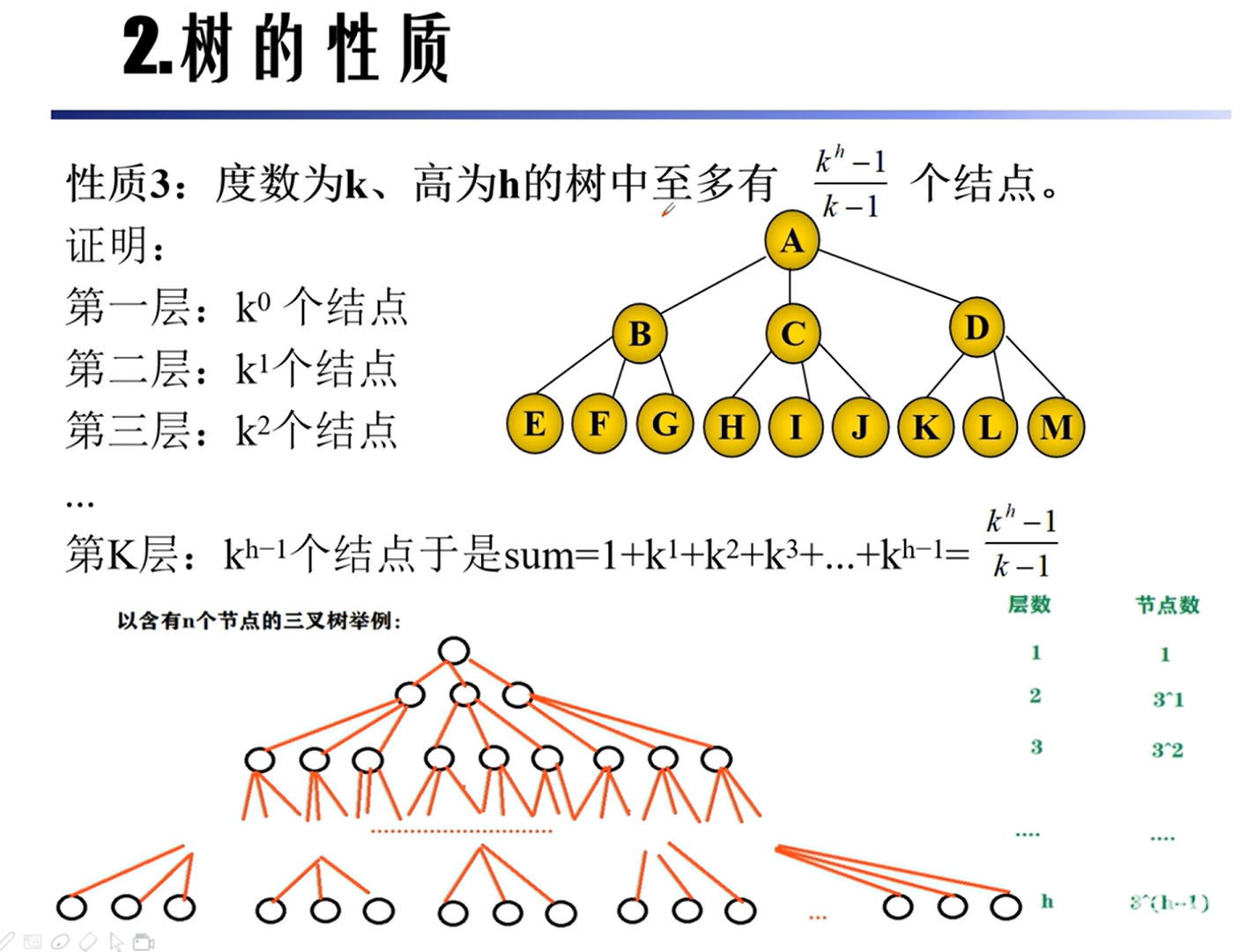
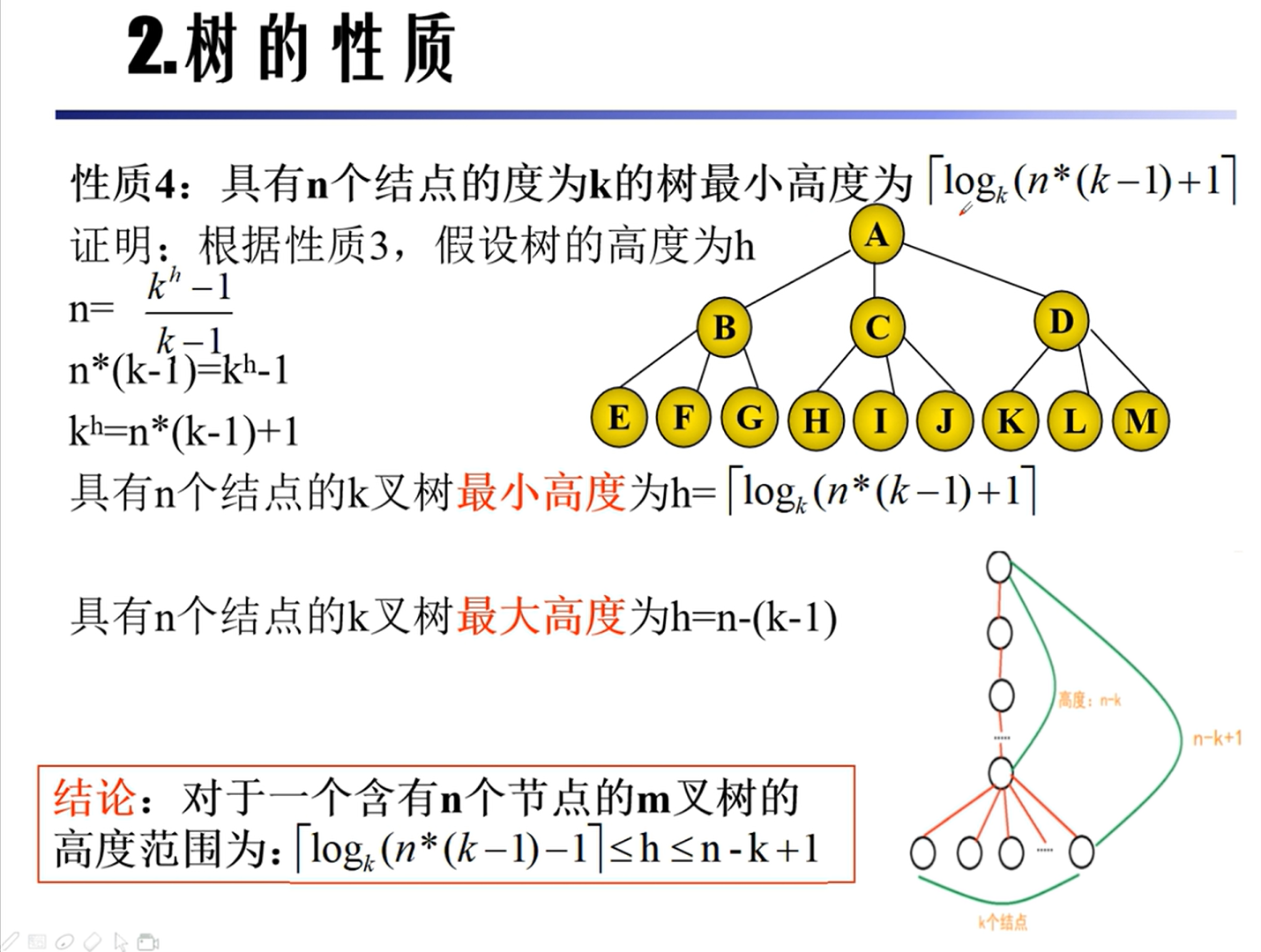
存储

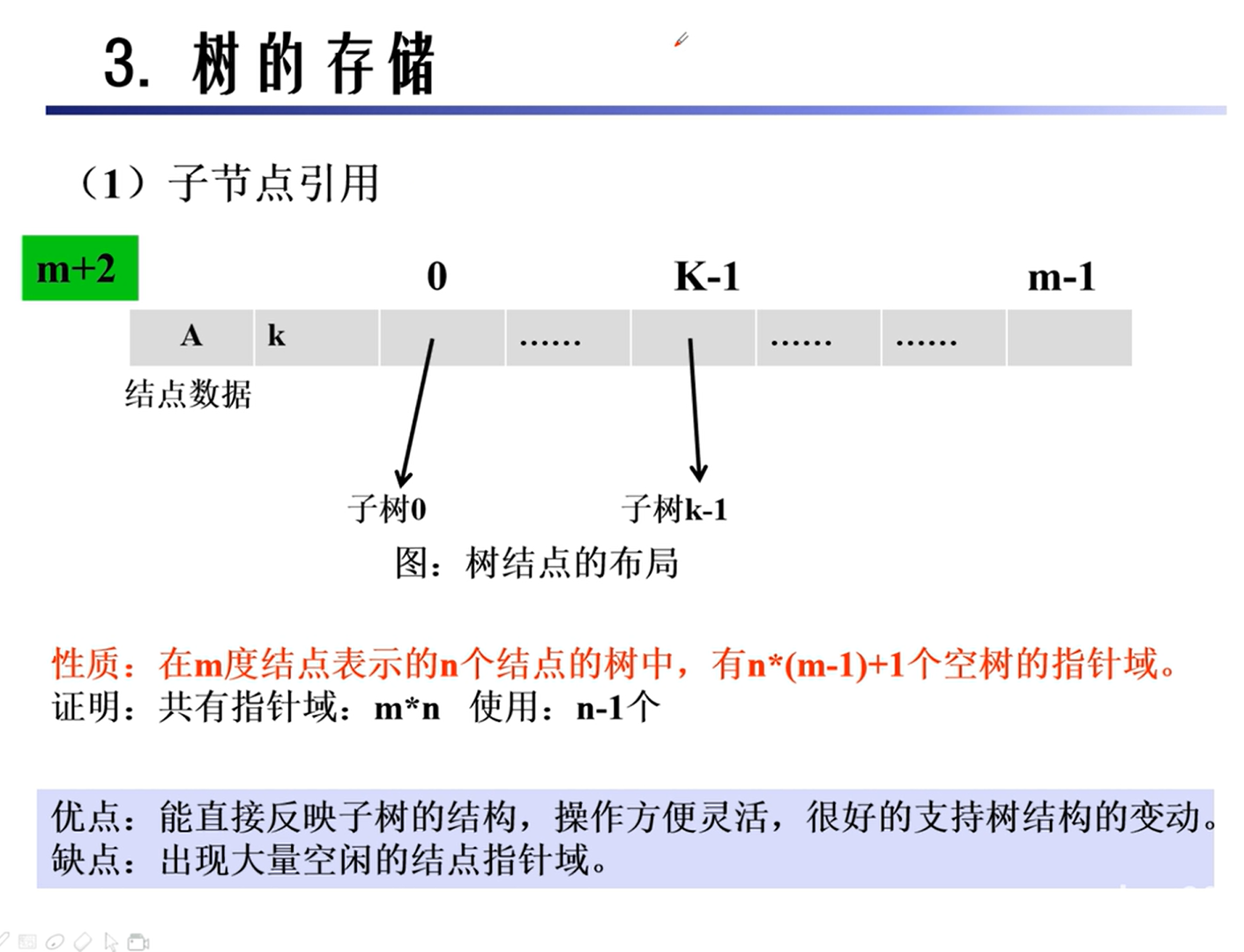
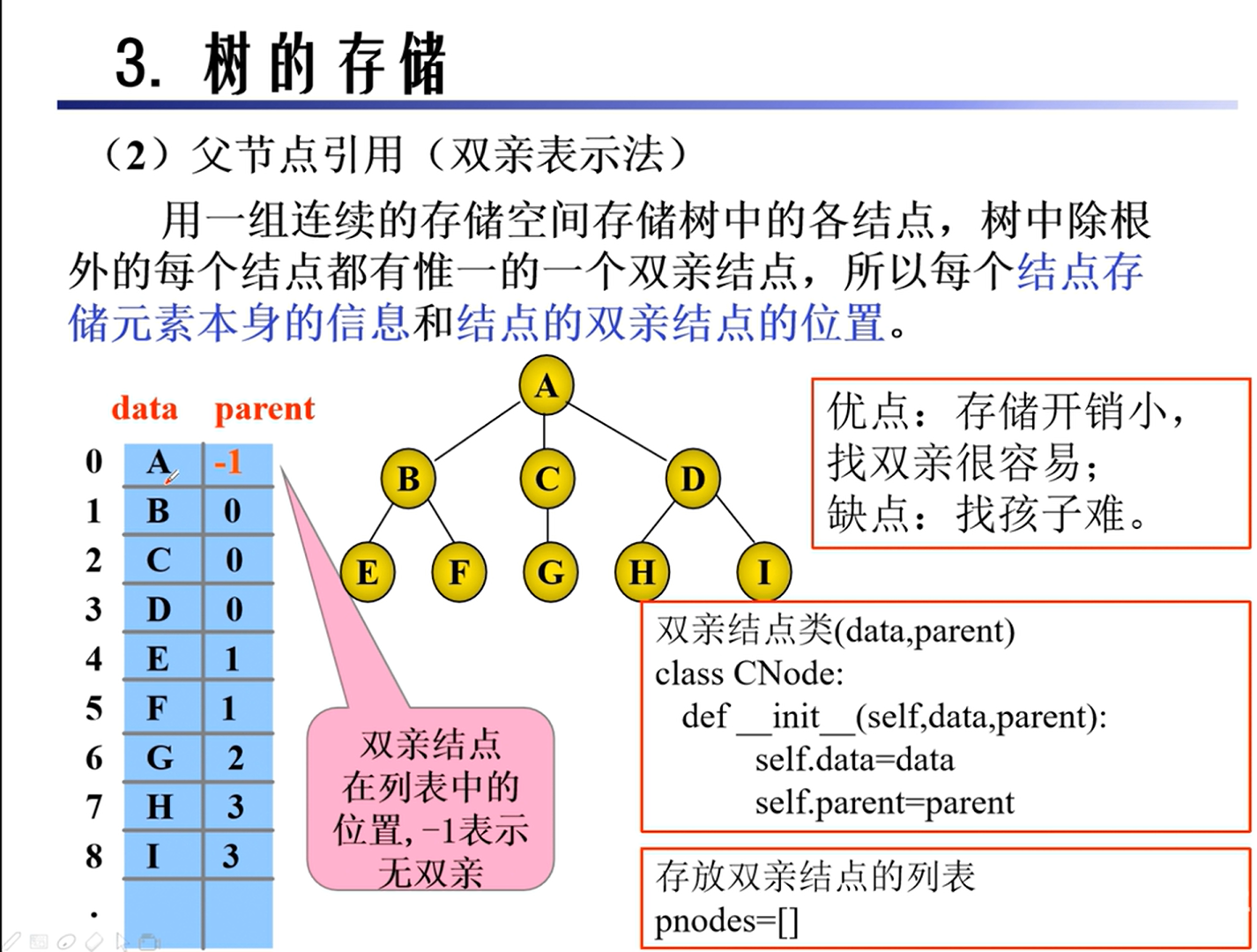
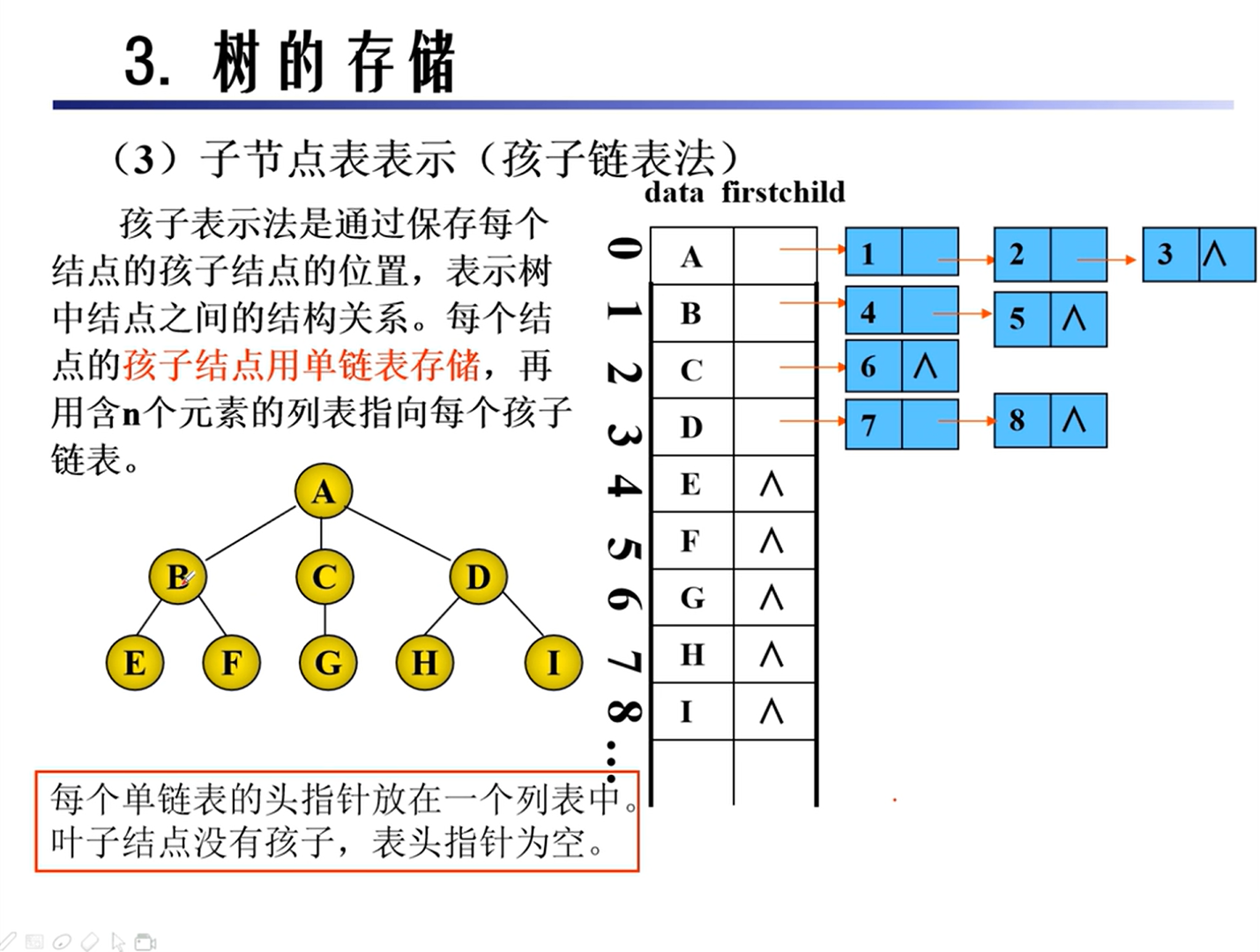
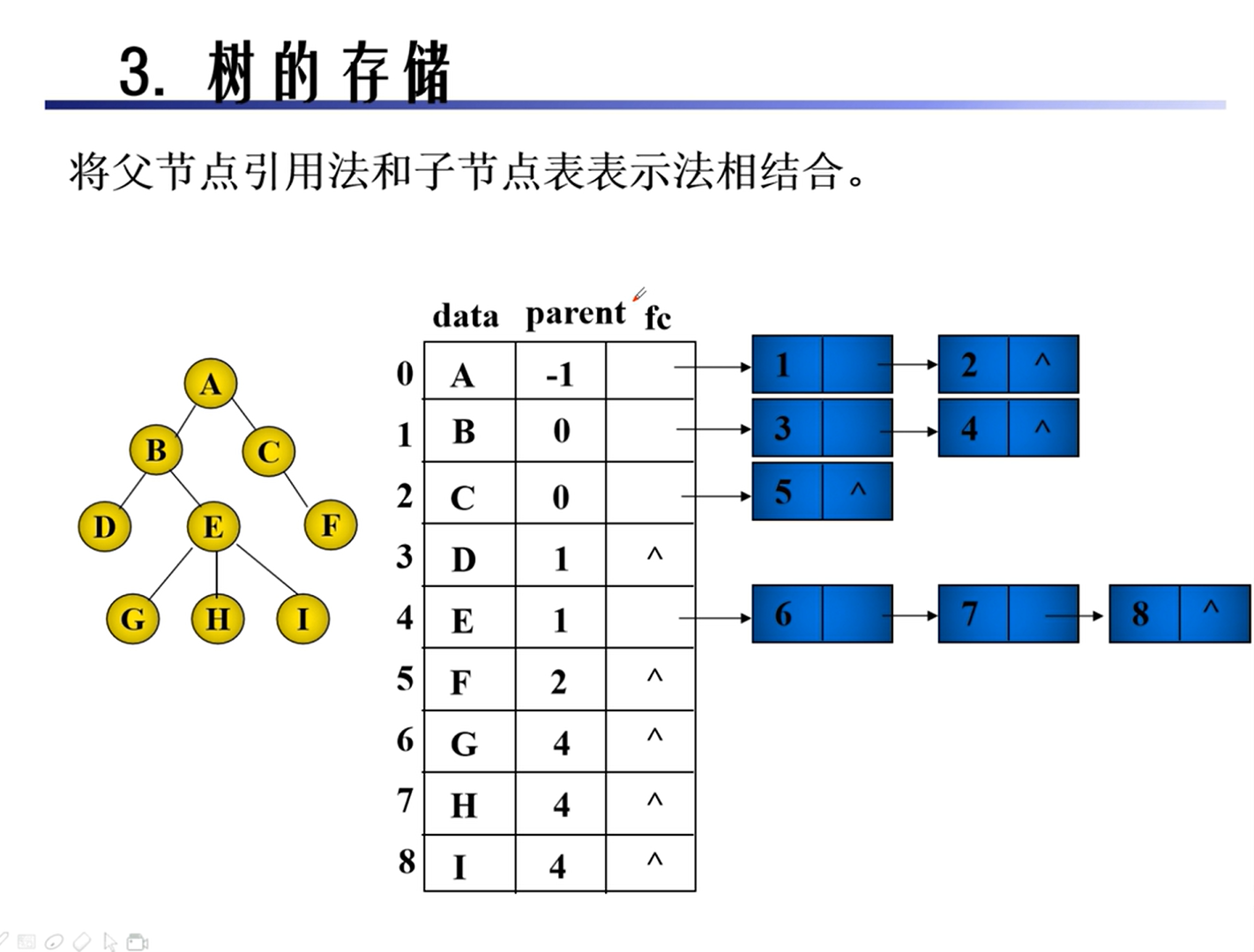
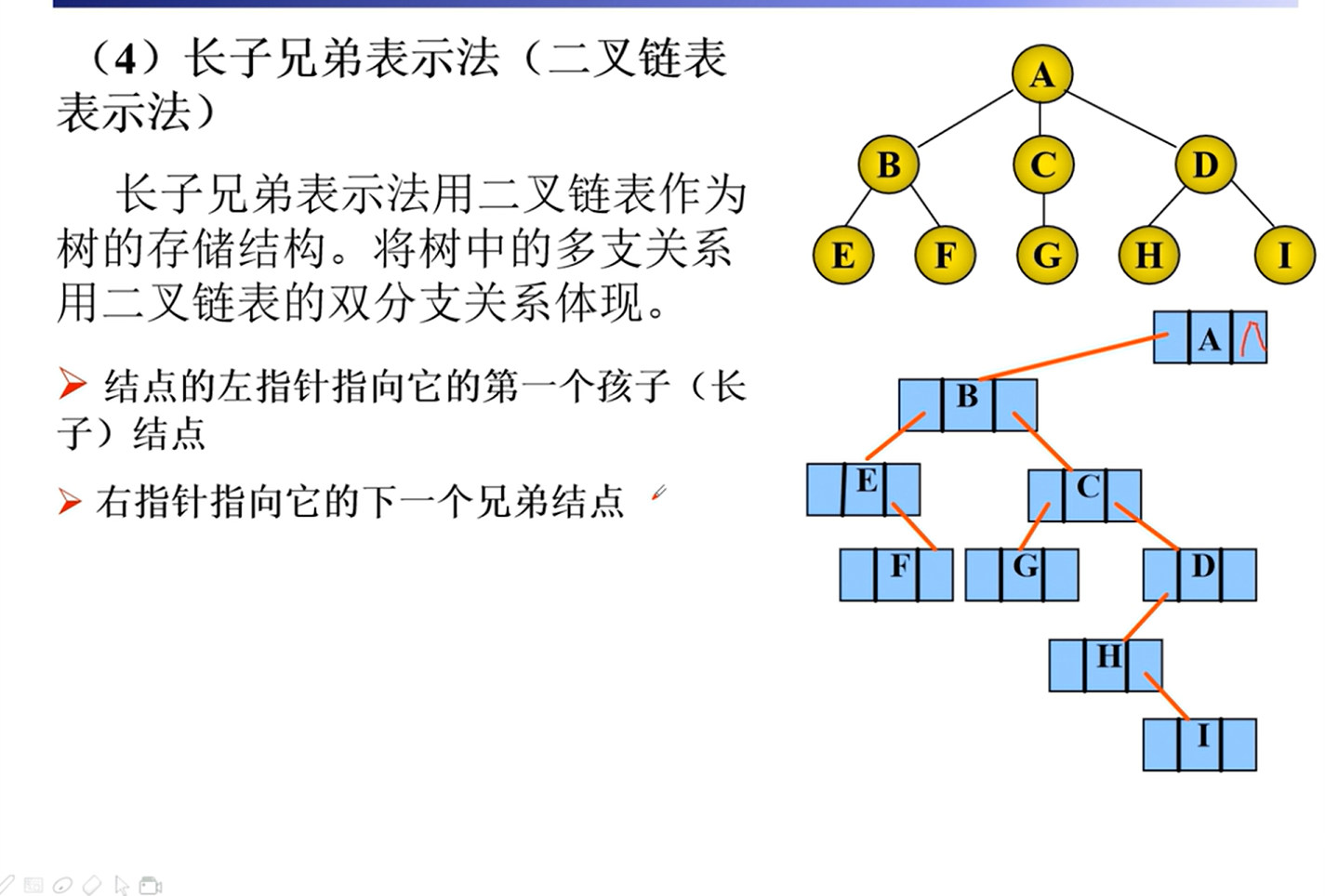
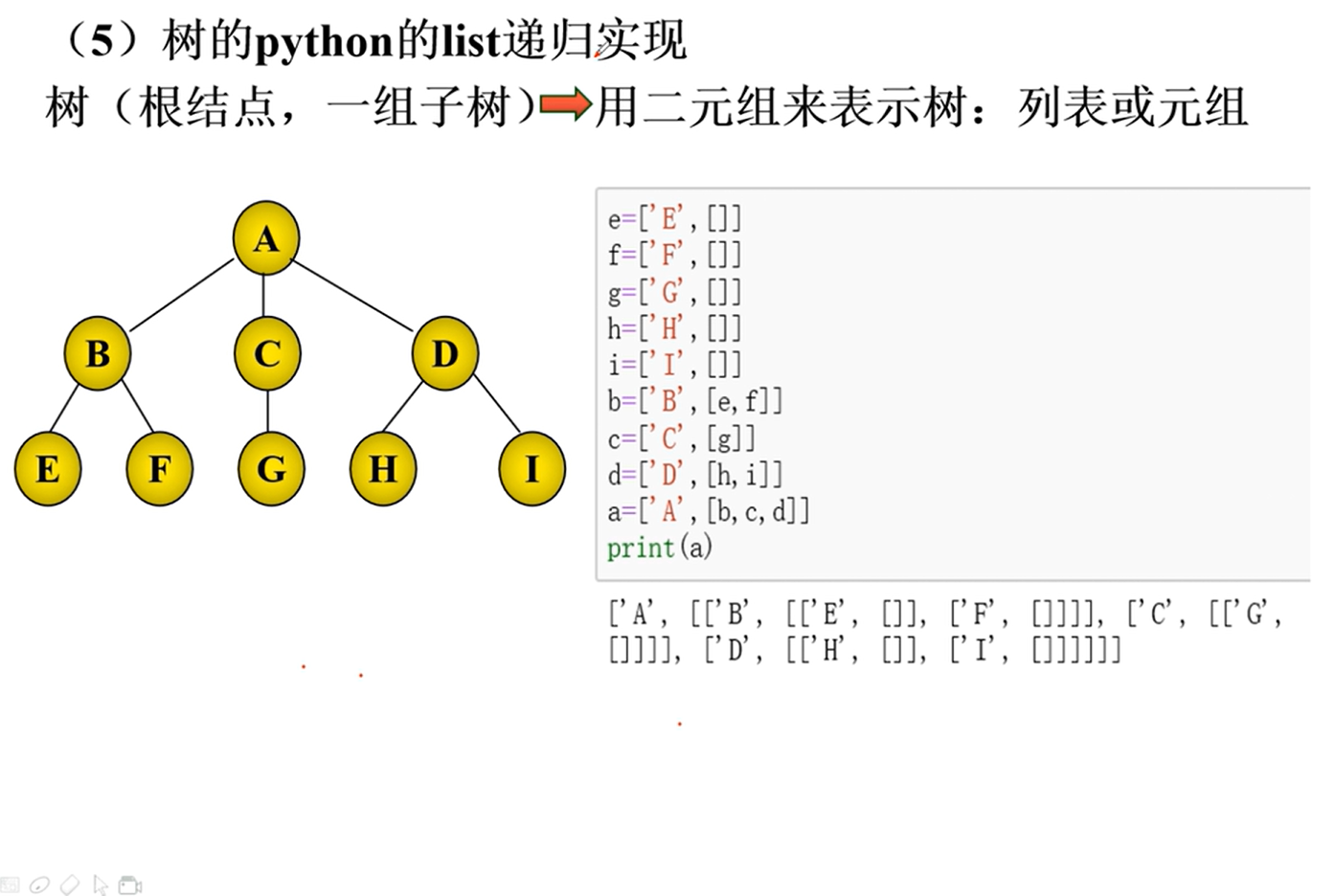
二叉树的转换

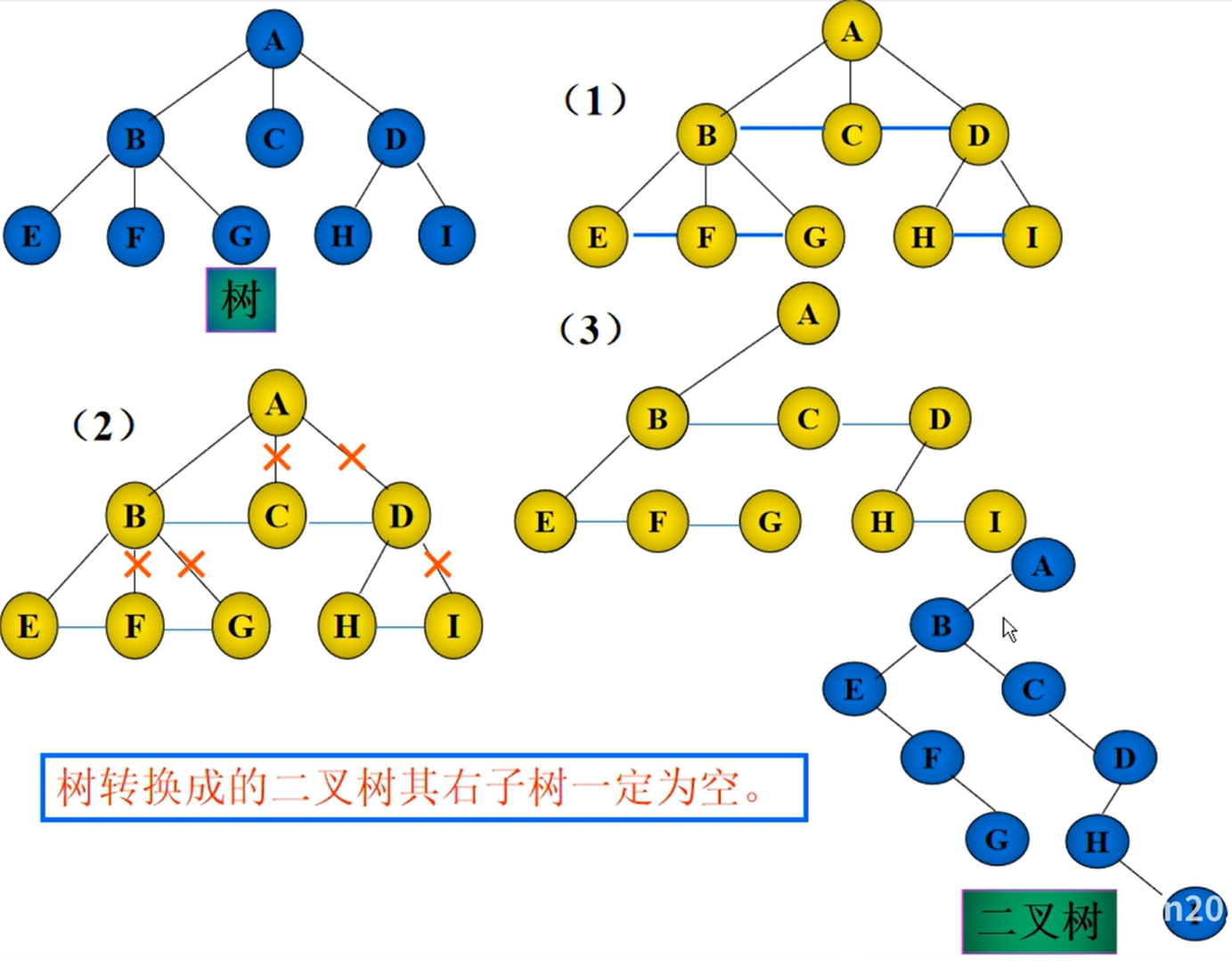

树和森林的转换
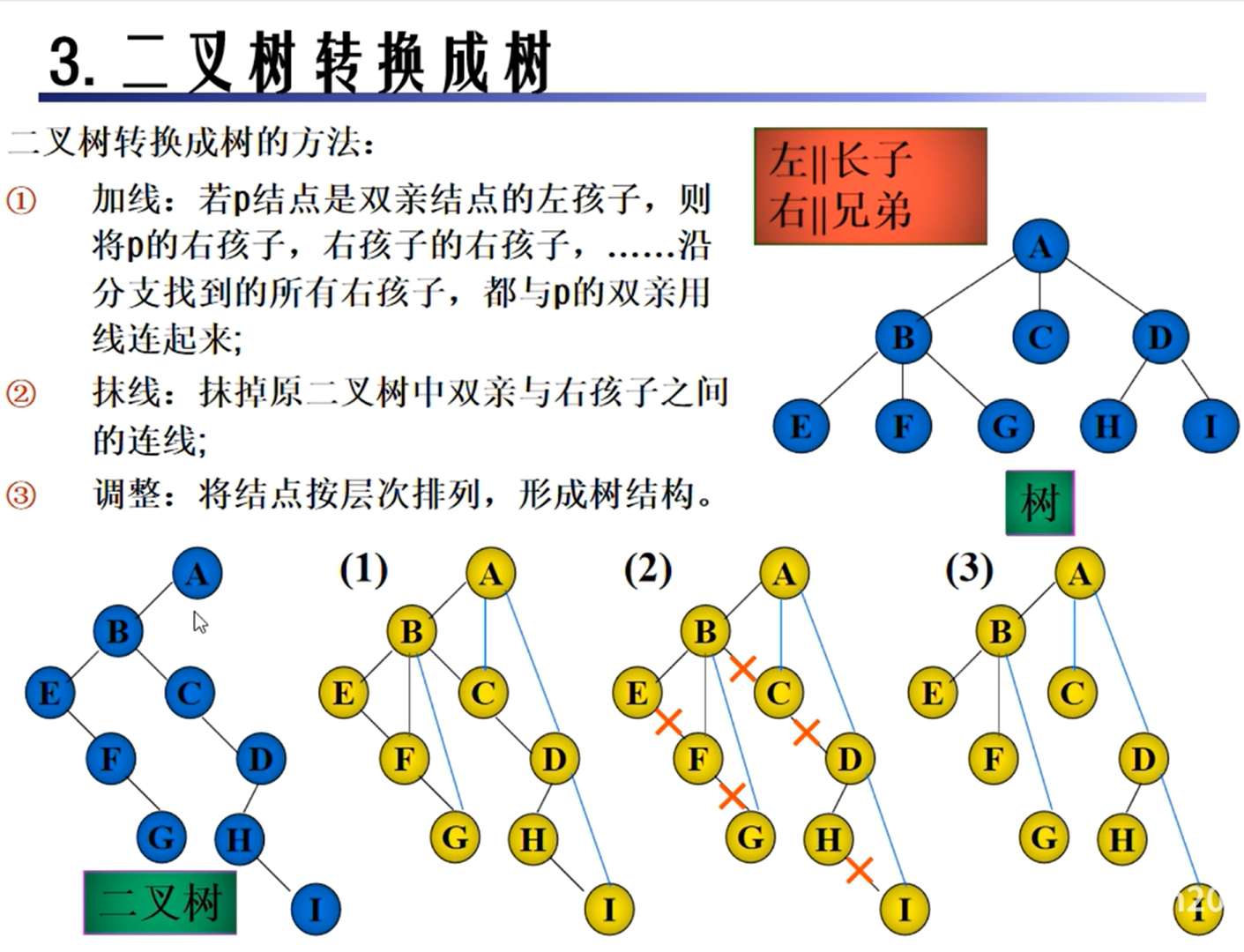
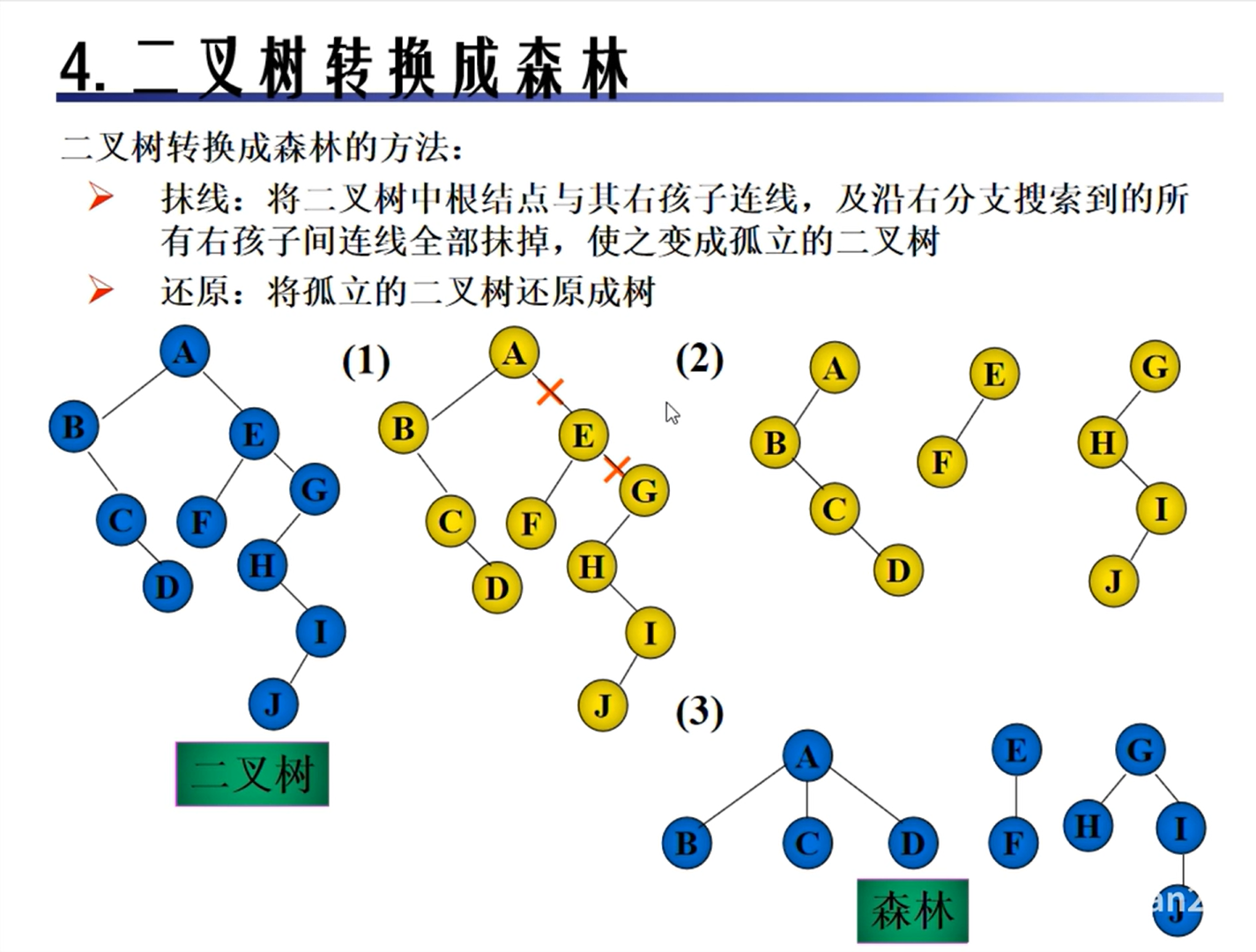







树的遍历
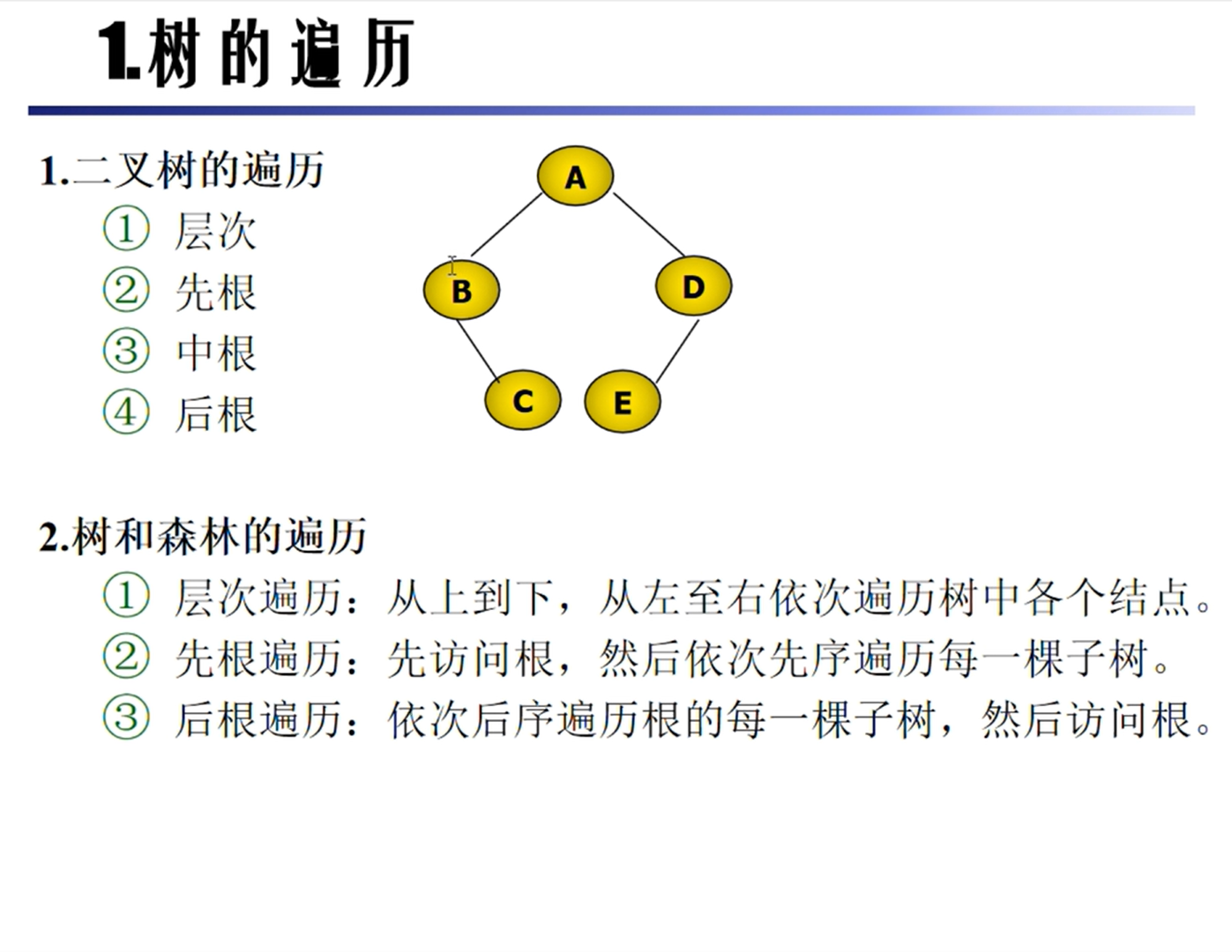
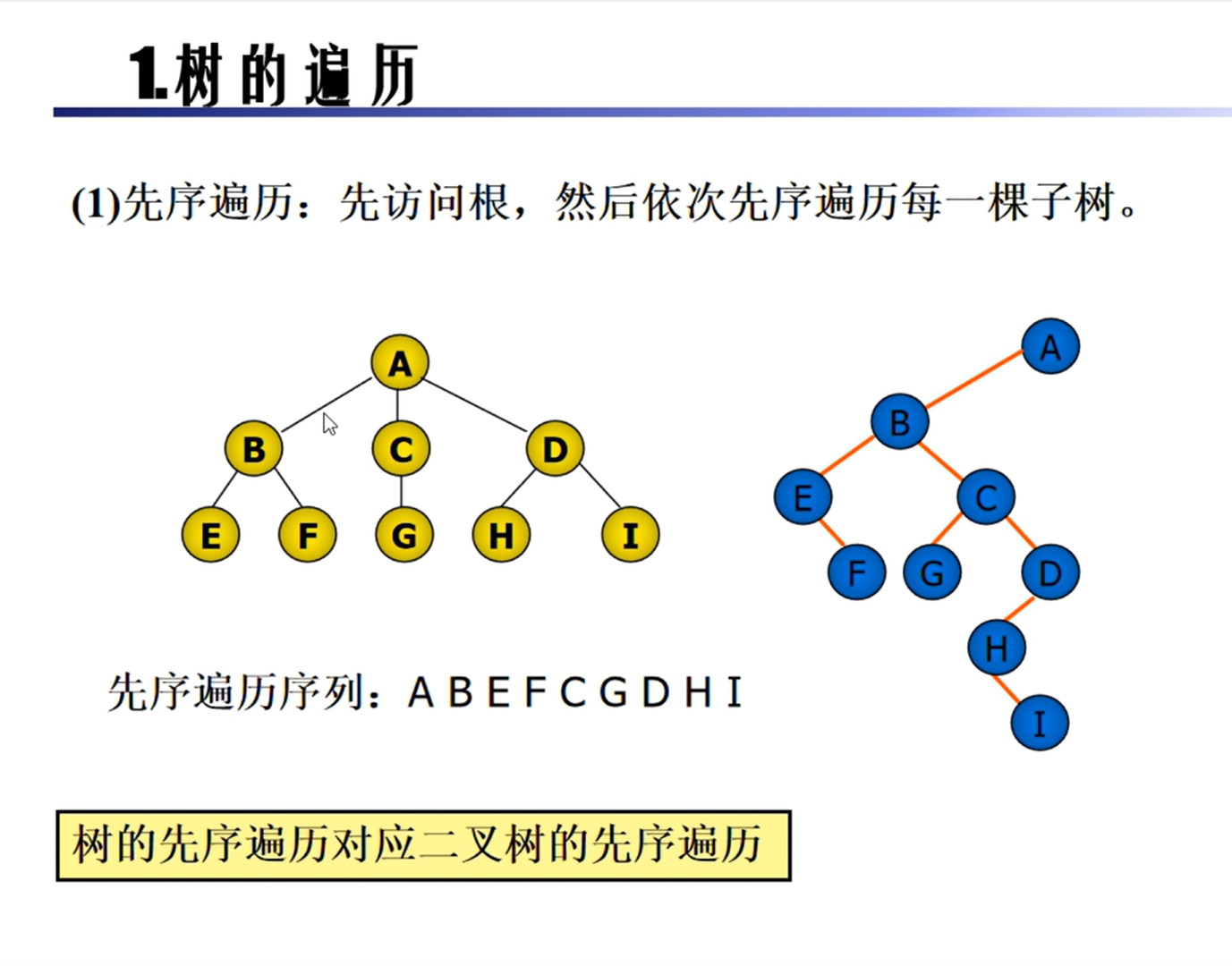
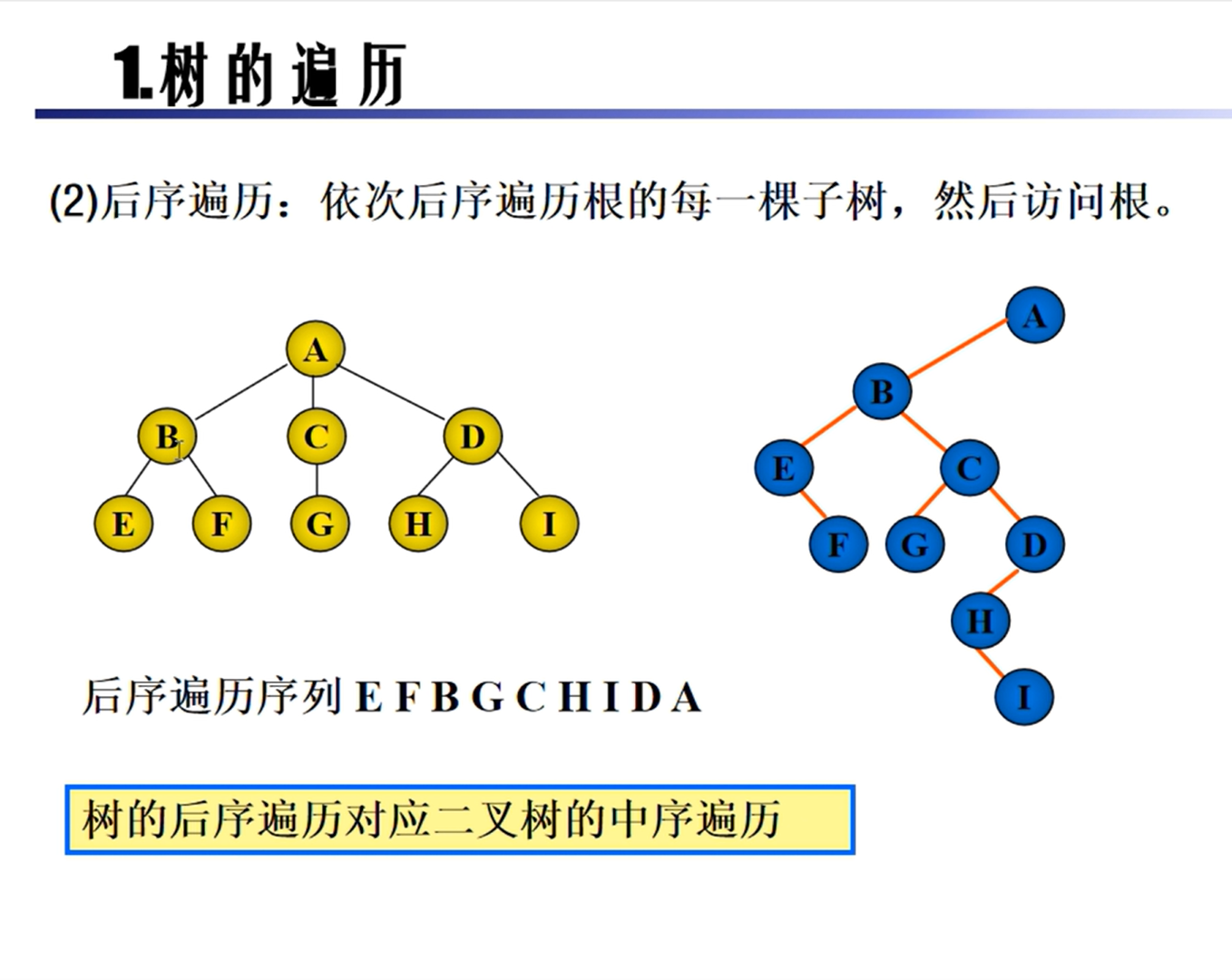
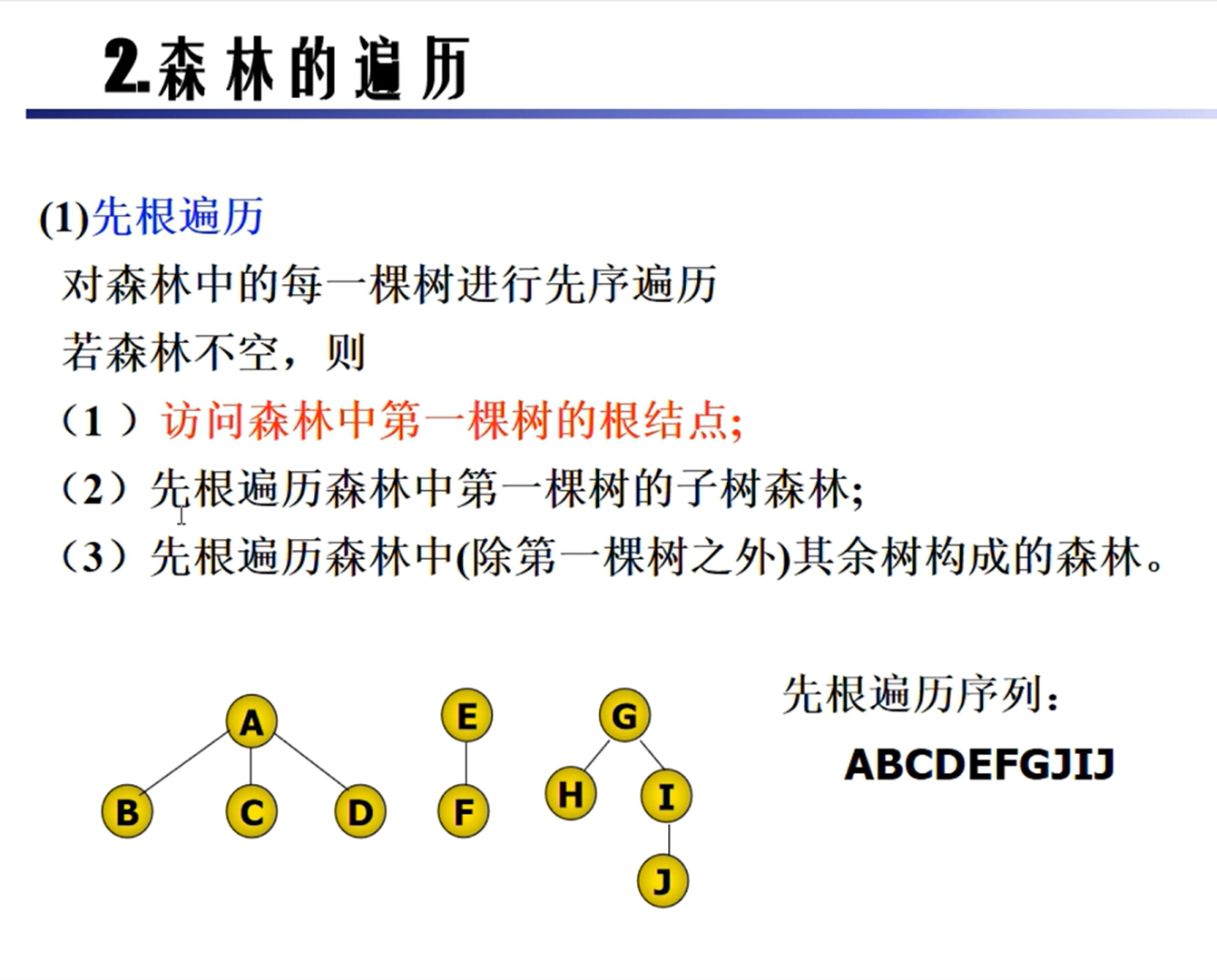
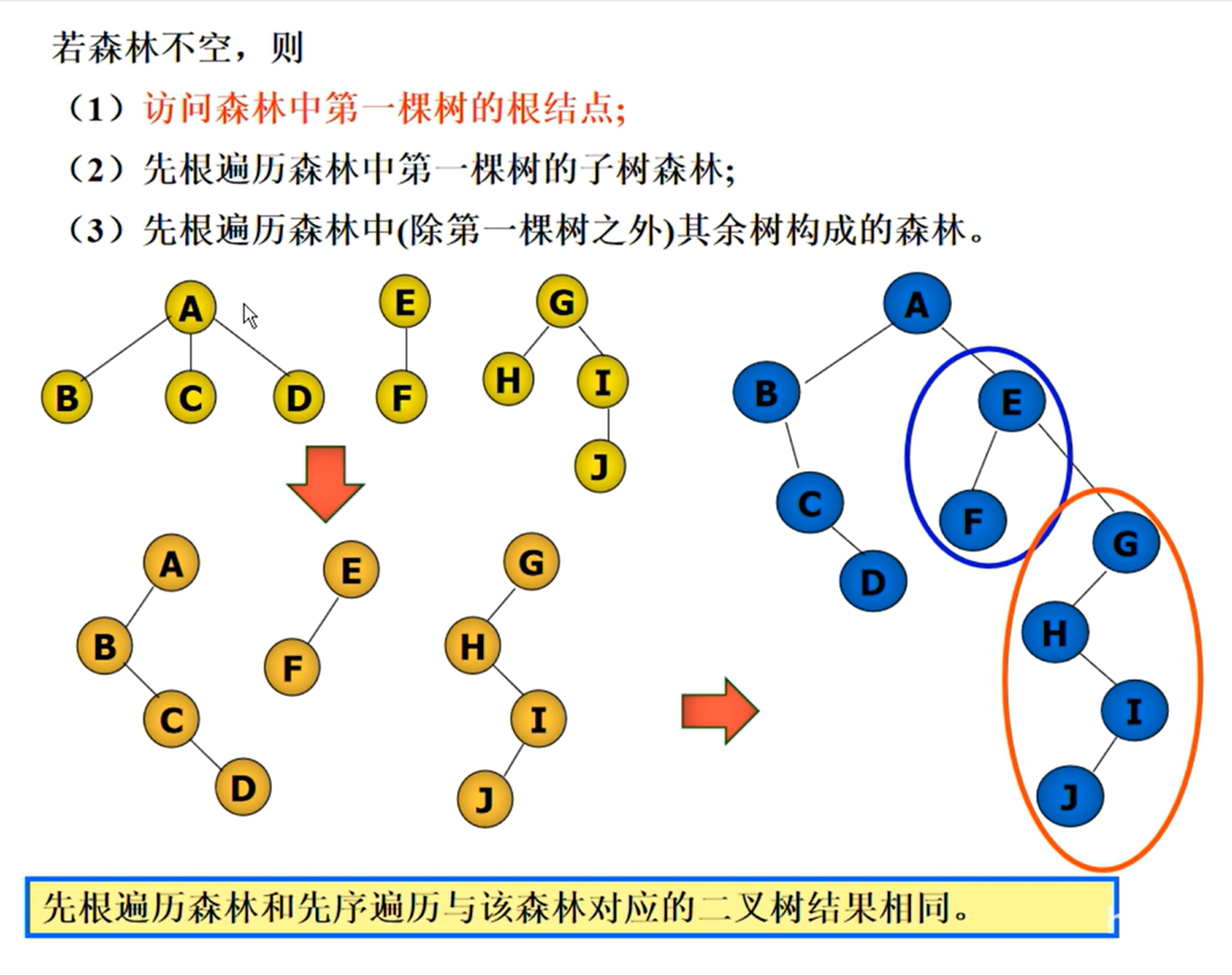
森林的遍历
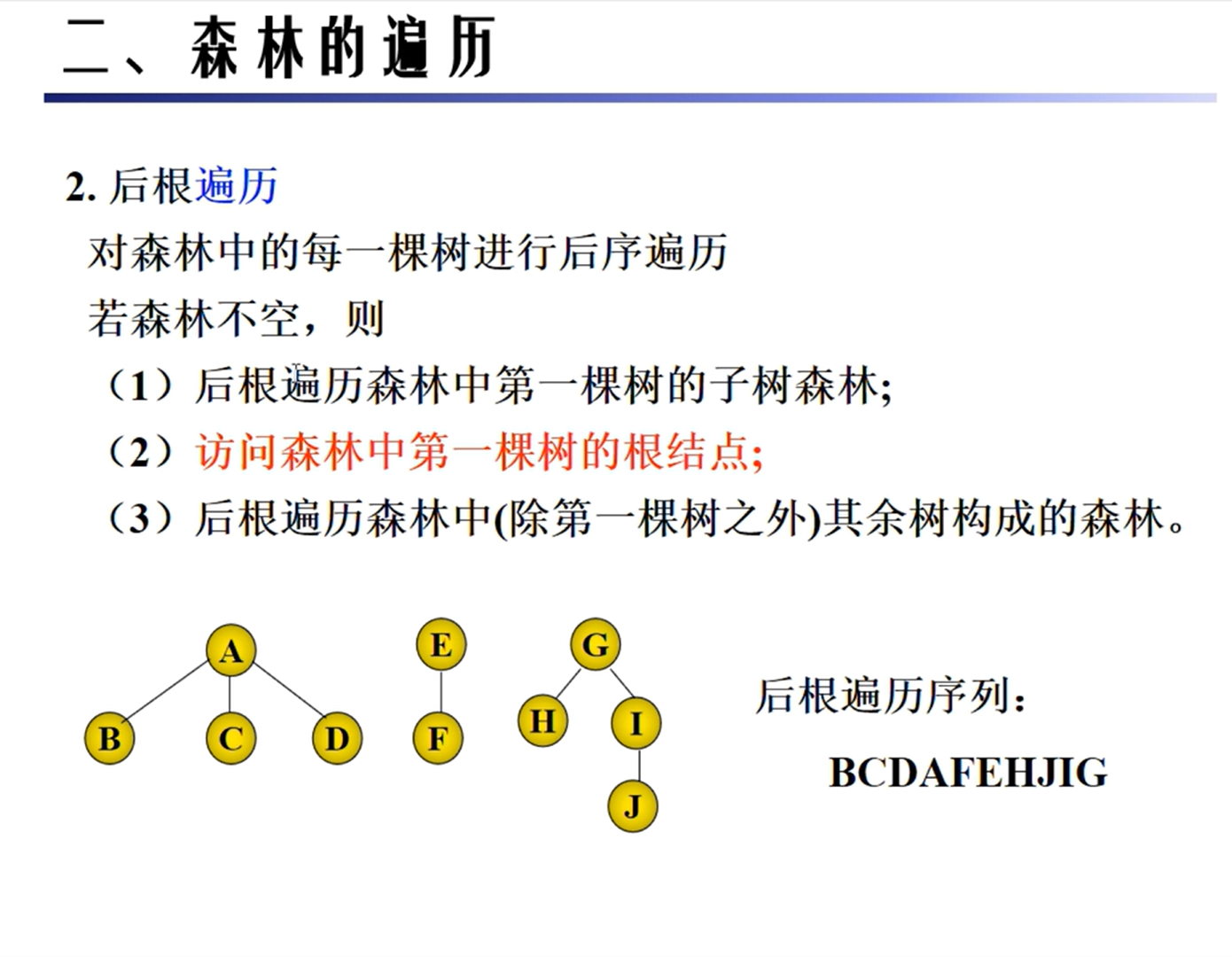
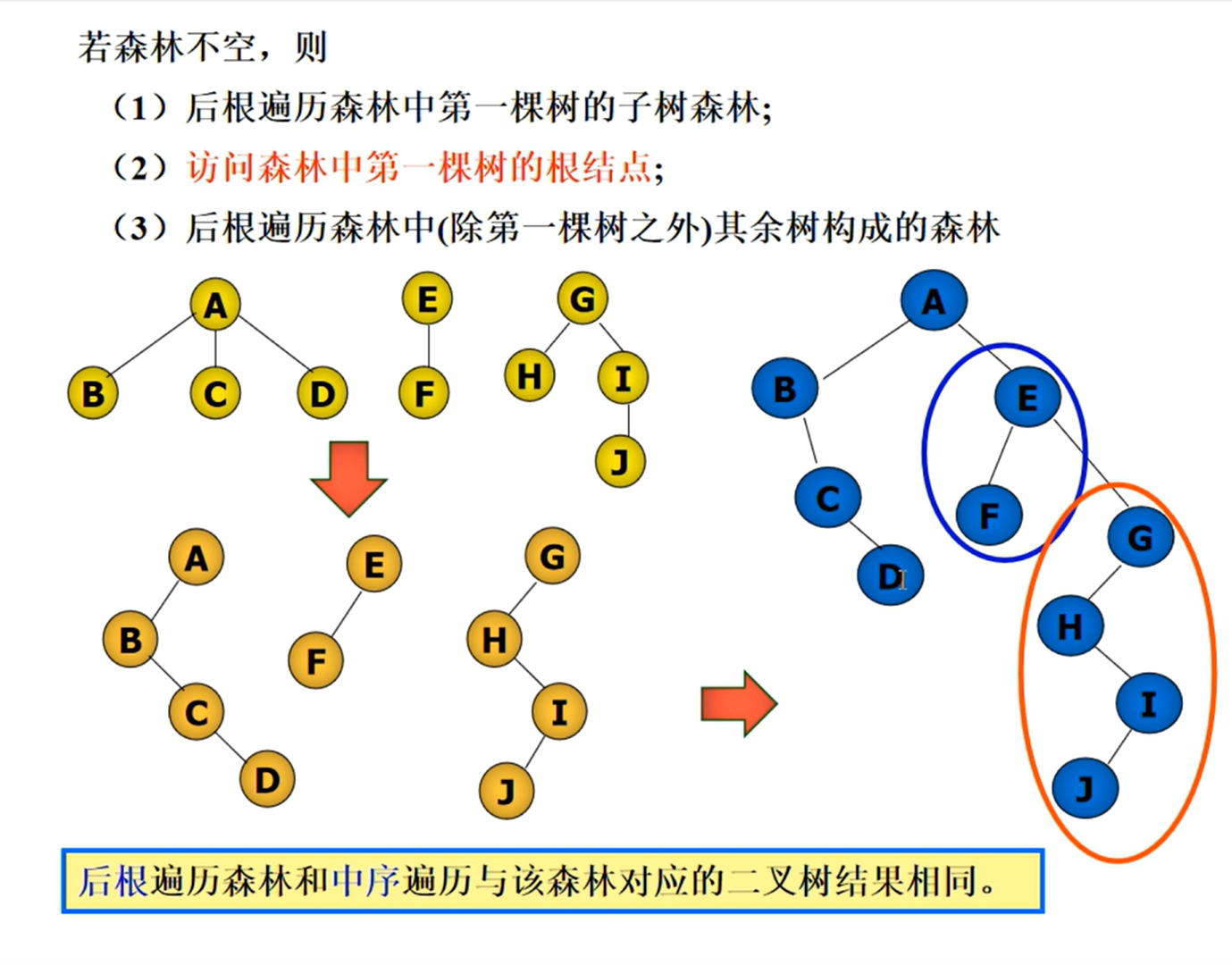
KMP匹配算法
class Solution:
def strStr(self, s: str, t: str) -> int:
'''KMP模板'''
def prefix_function(s):
n = len(s)
pi = [0] * n
j = 0
for i in range(1, n):
while j>0 and s[i] != s[j]: # 当前位置s[i]与s[j]不等
j = pi[j-1] # j指向之前位置,s[i]与s[j]继续比较
if s[i] == s[j]: # s[i]与s[j]相等,j+1,指向后一位
j += 1
pi[i] = j
return pi
'''主程序'''
n, m = len(s), len(t)
pi = prefix_function(t) # 预处理得到t的前缀函数
'''再次基于KMP的思想在s中匹配t'''
j = 0
for i in range(n):
while j>0 and s[i] != t[j]:
j = pi[j-1]
if s[i] == t[j]:
j += 1
if j == m: # 匹配到了t,直接返回
return i-m+1
return -1
图
基本概念
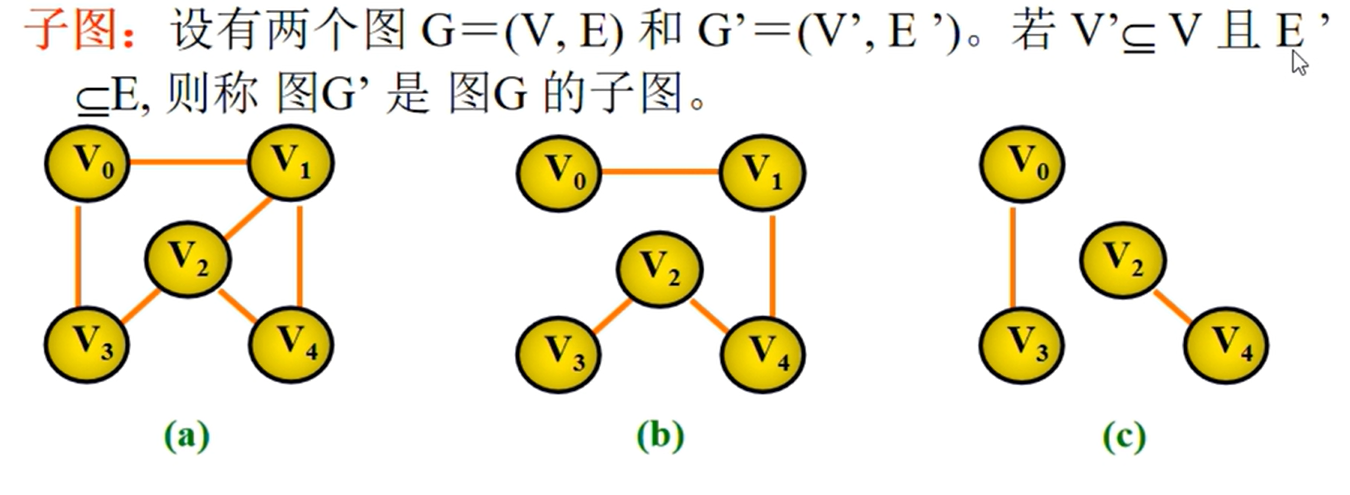
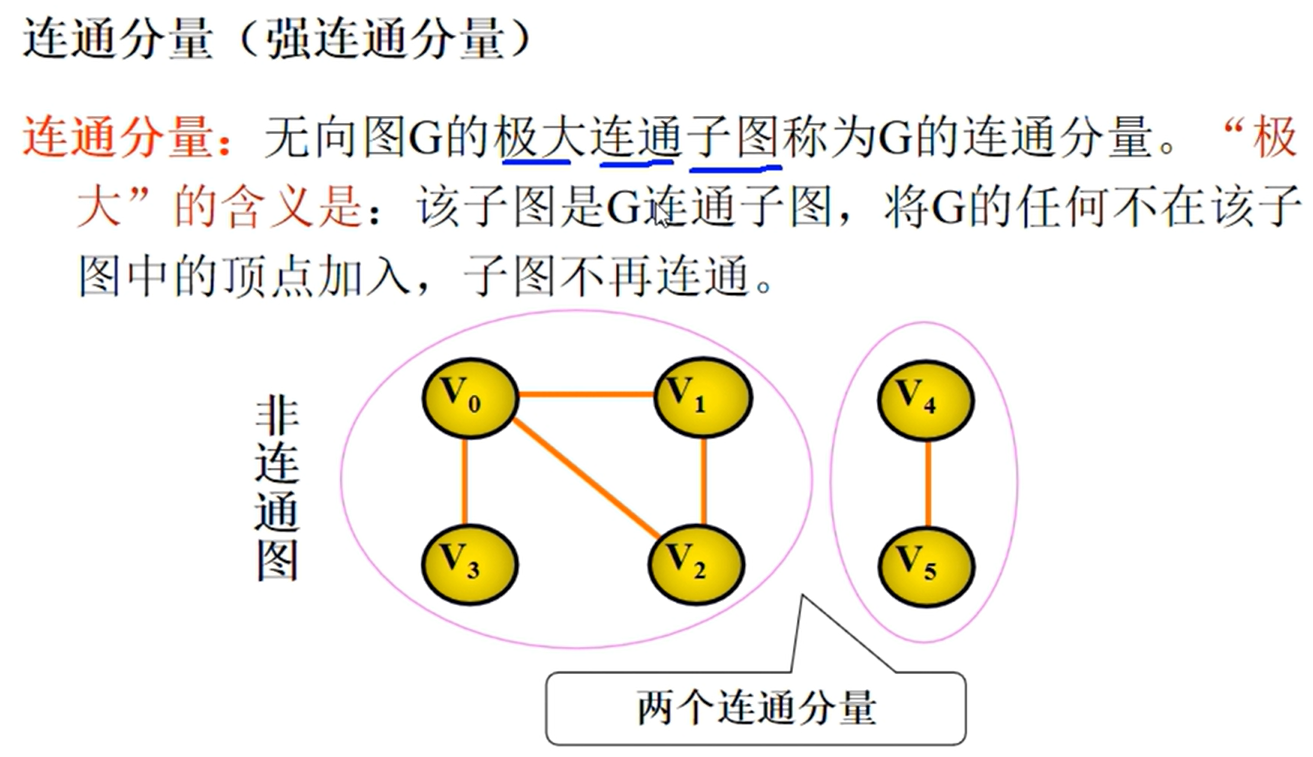
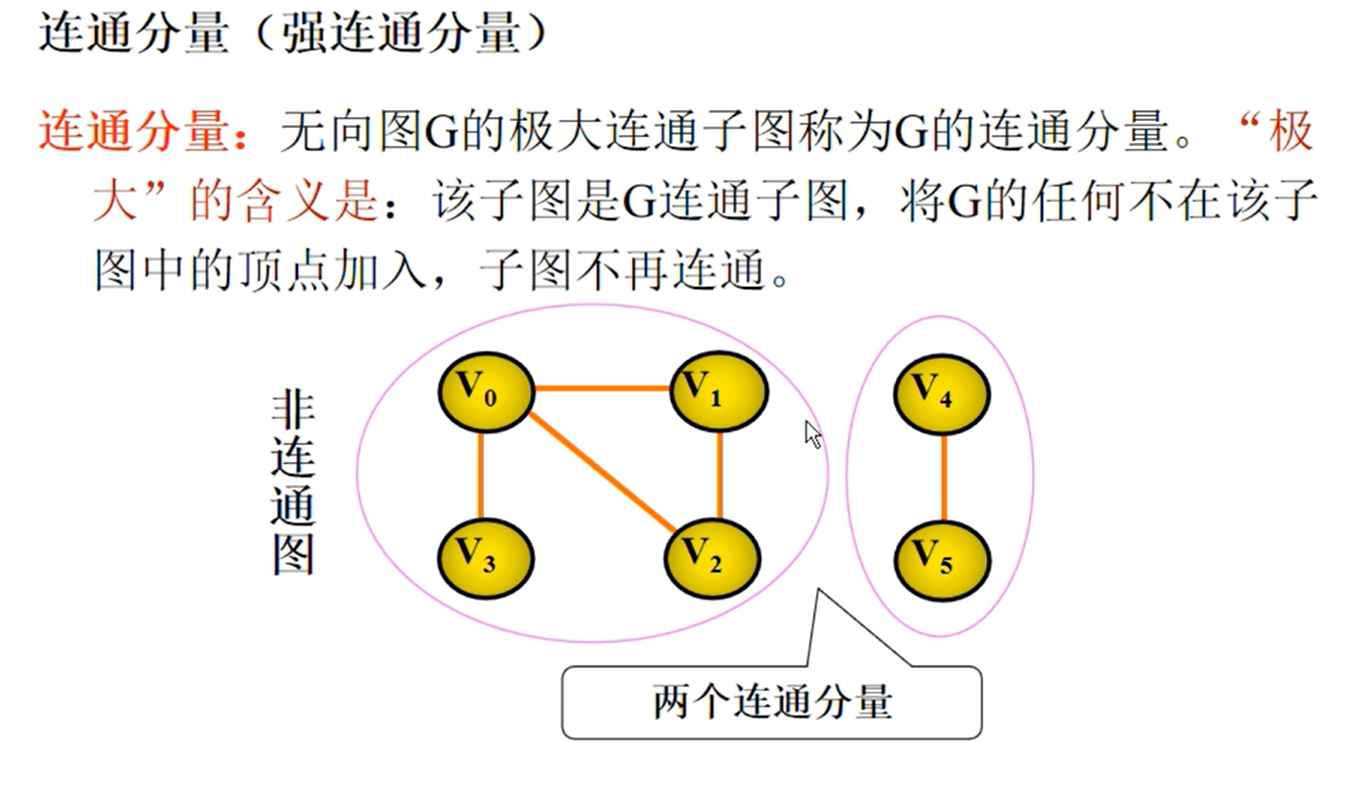
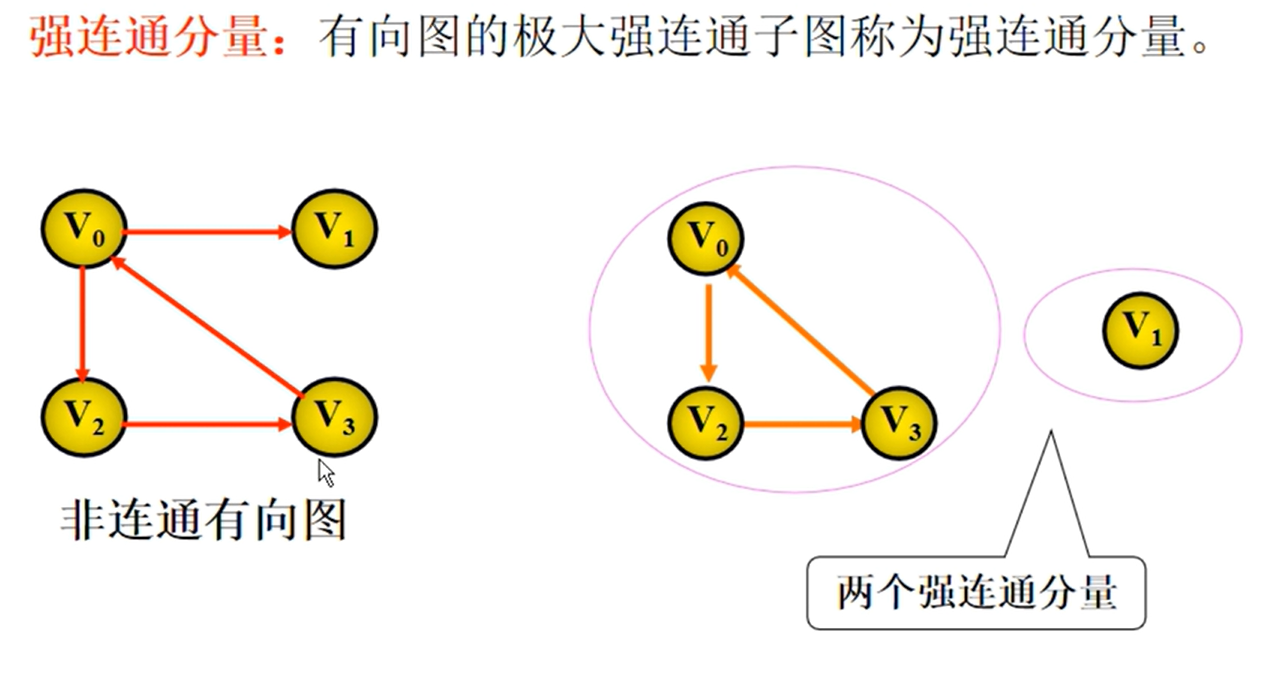
图的定义
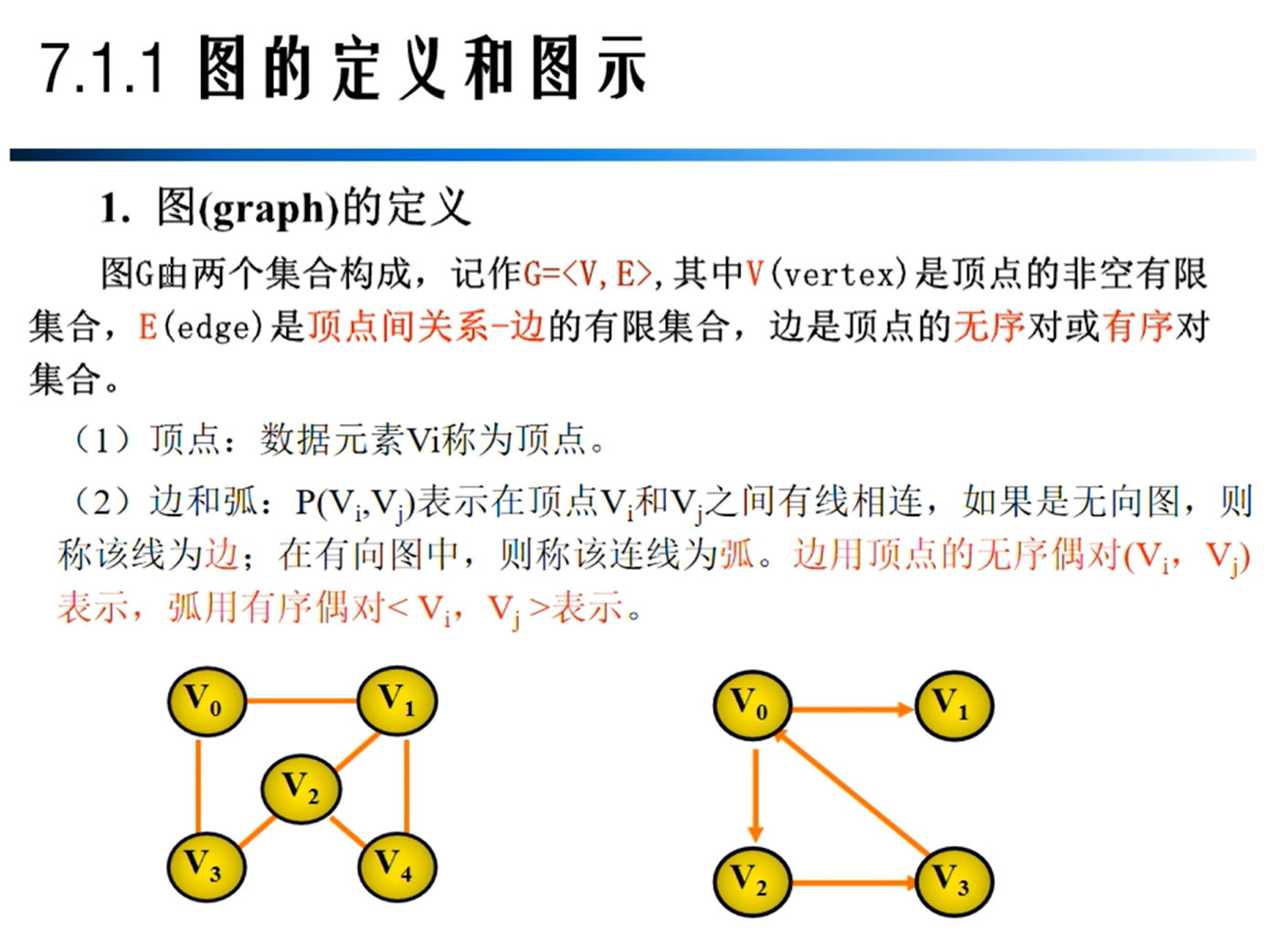

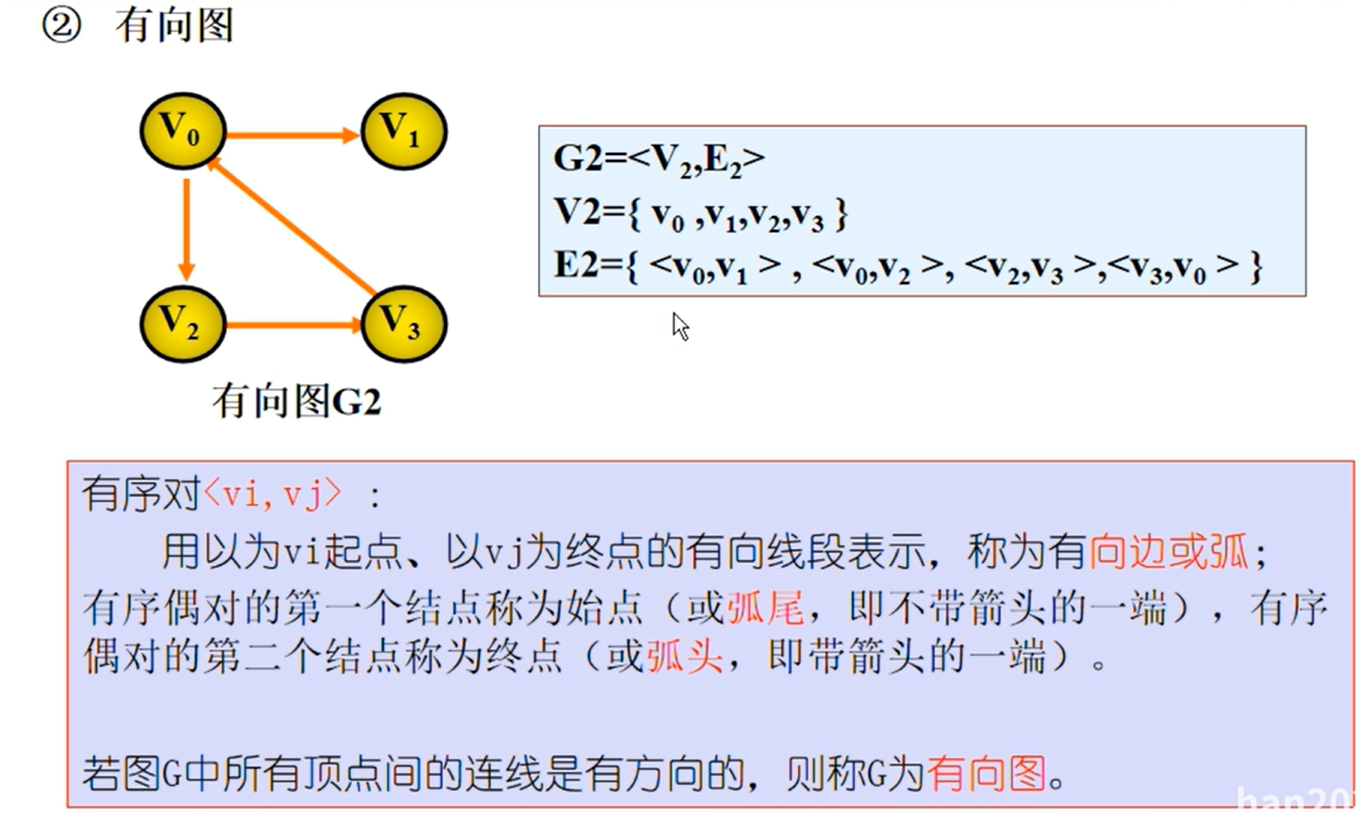
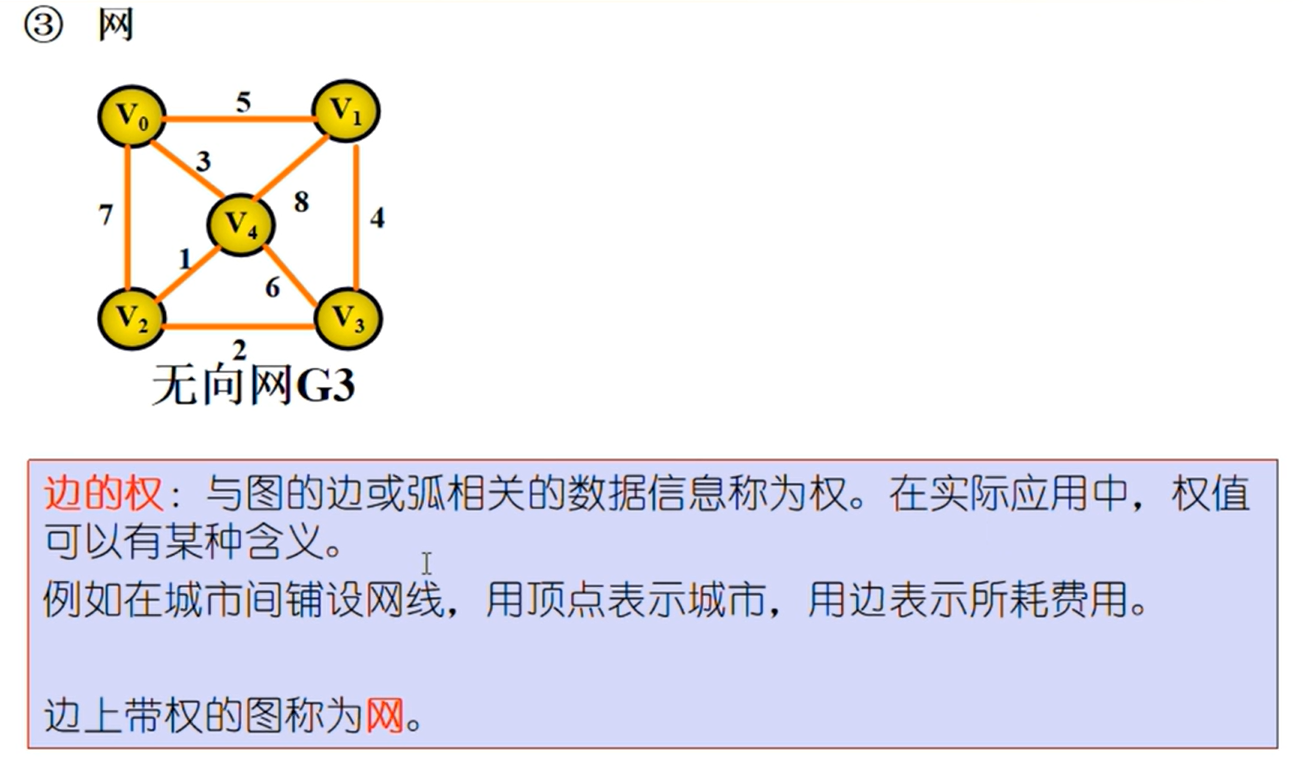
图的相关概念
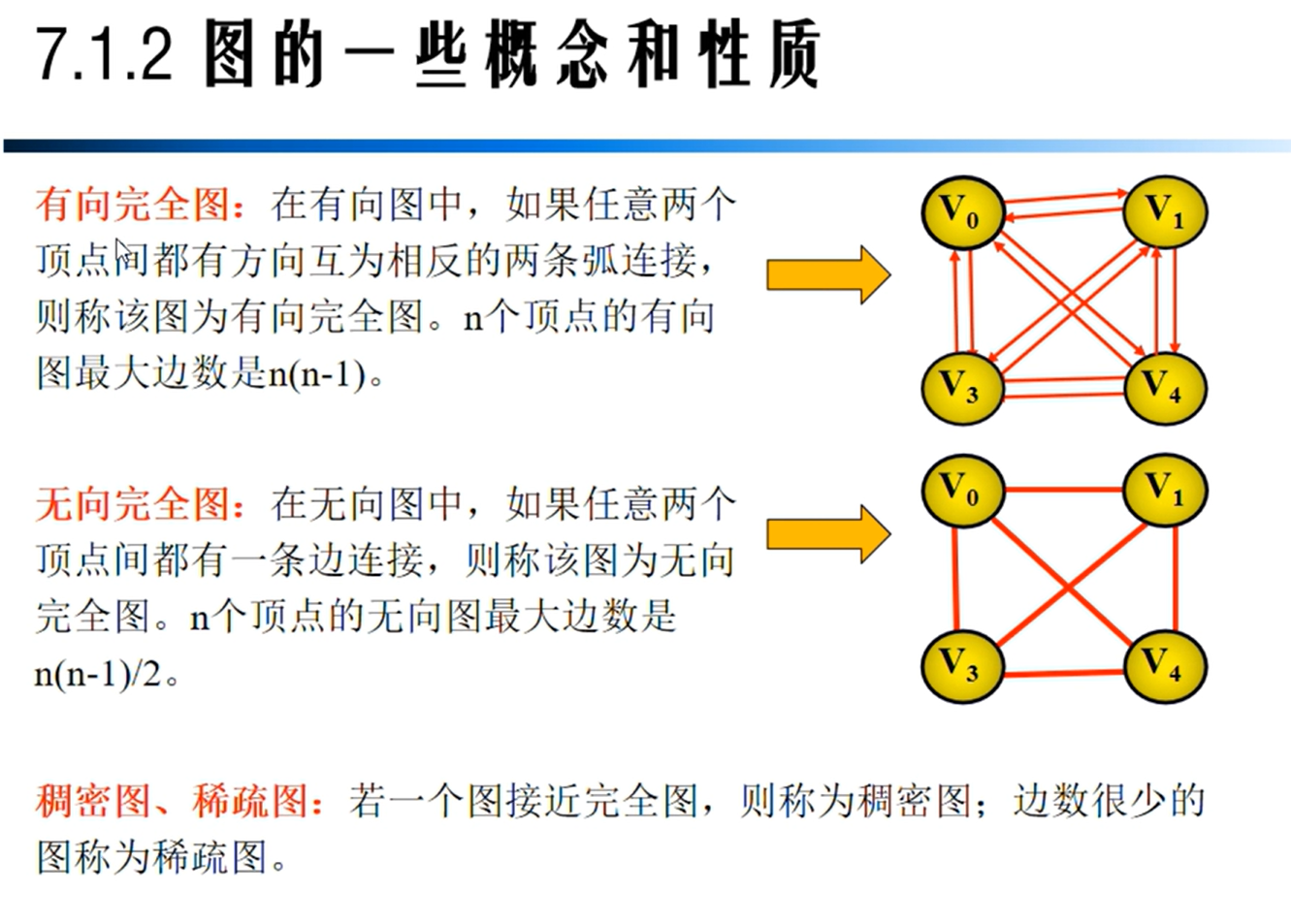
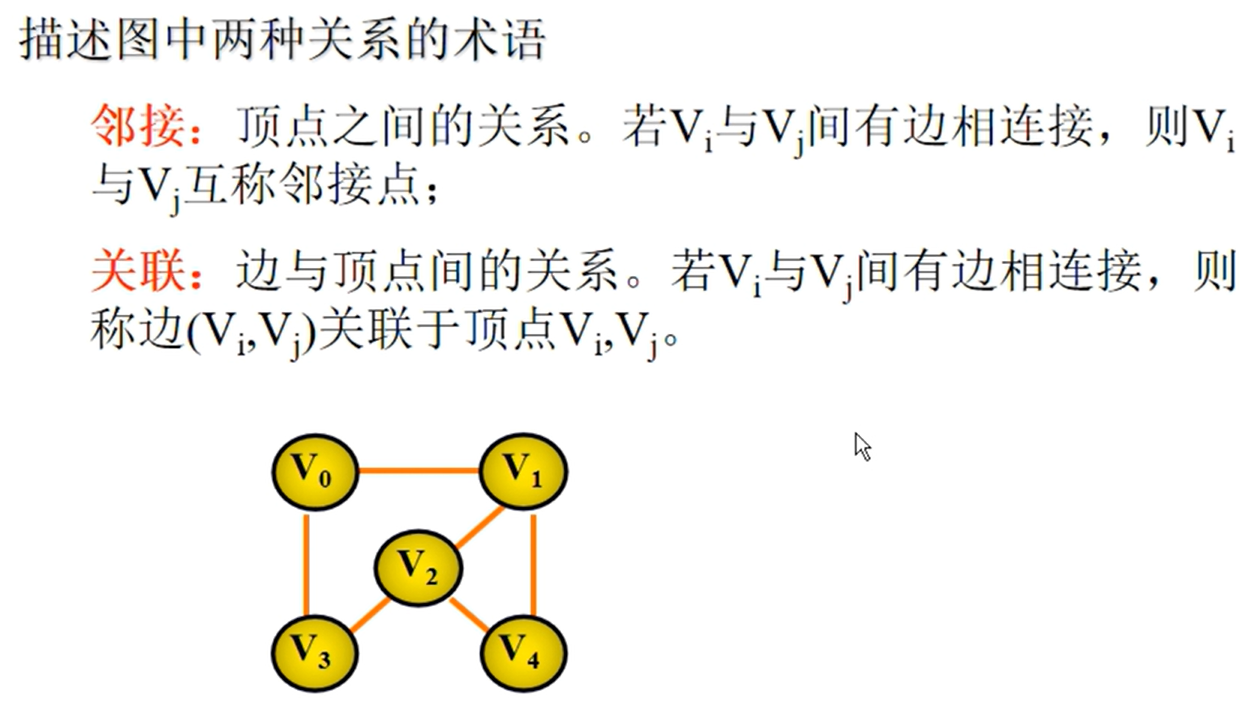
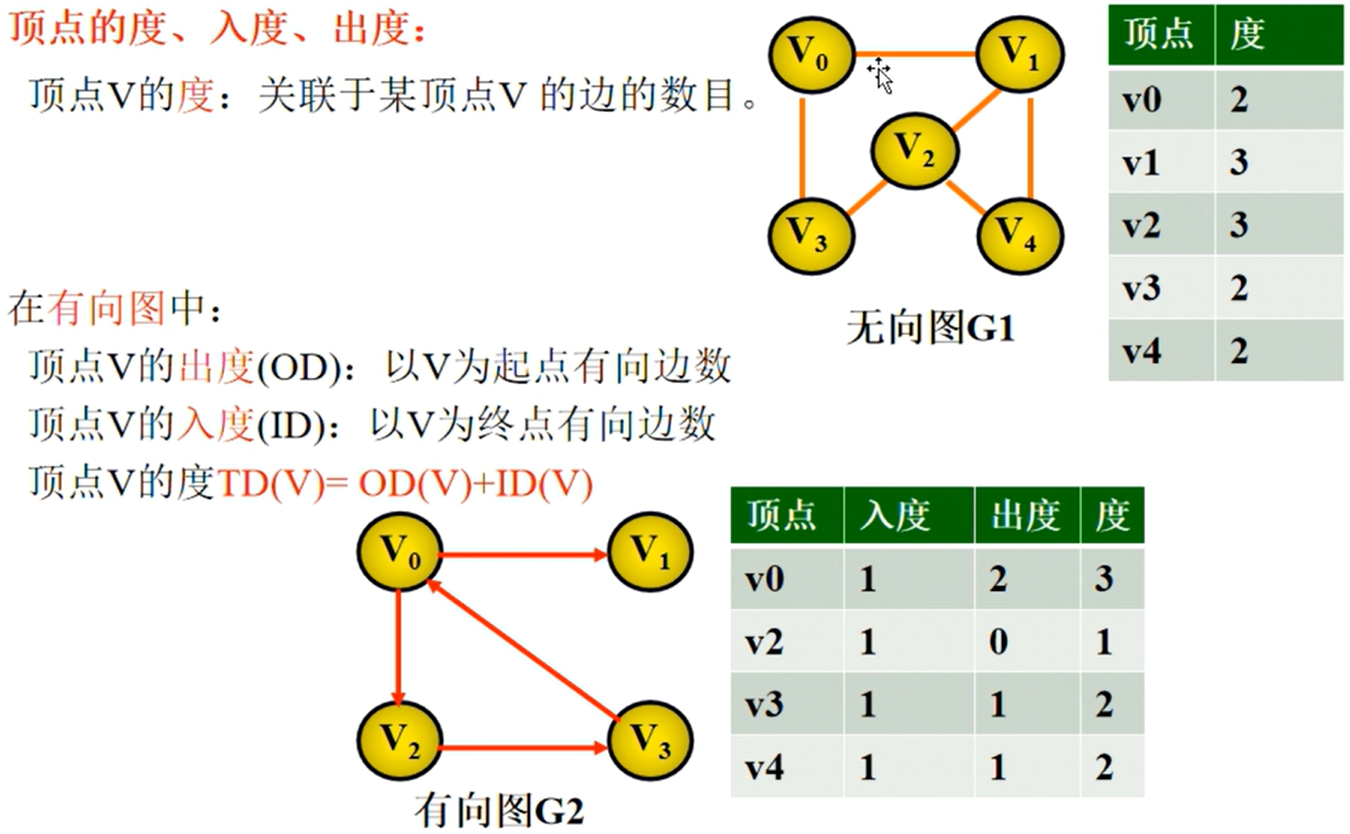
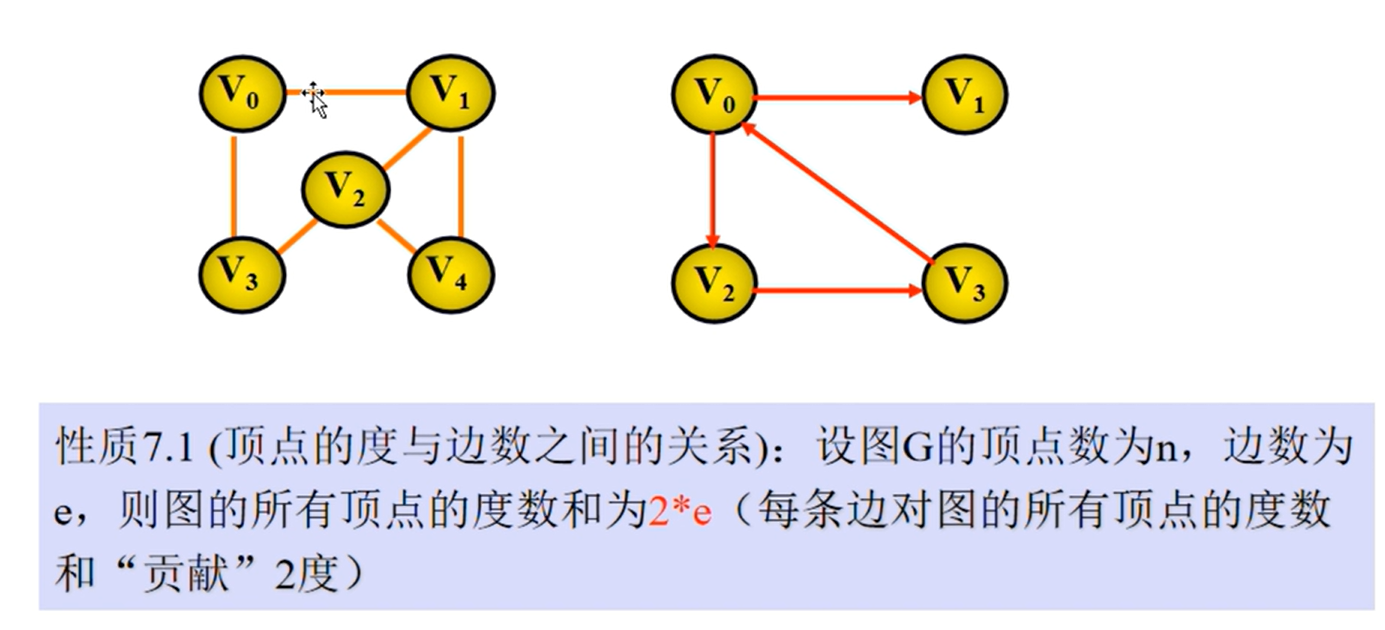
图的相关性质
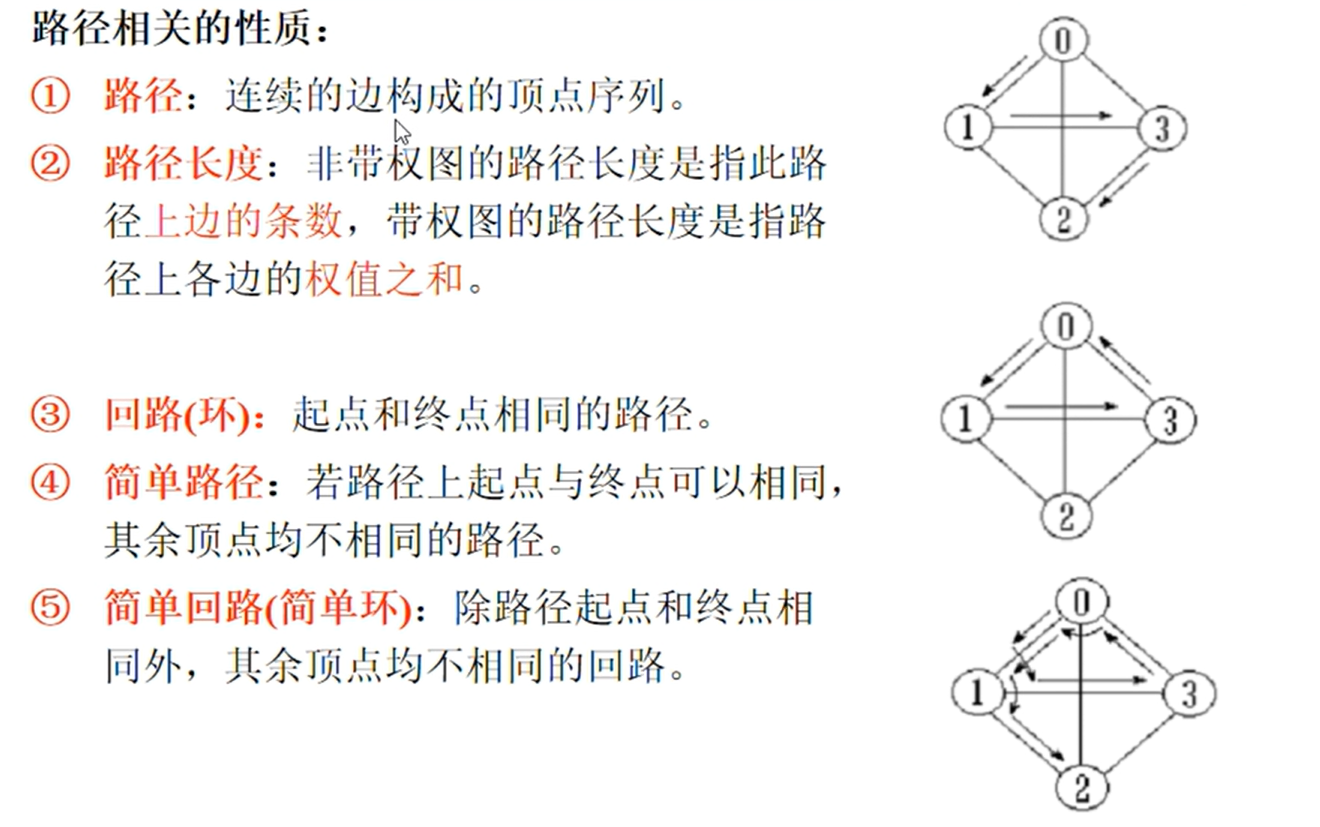
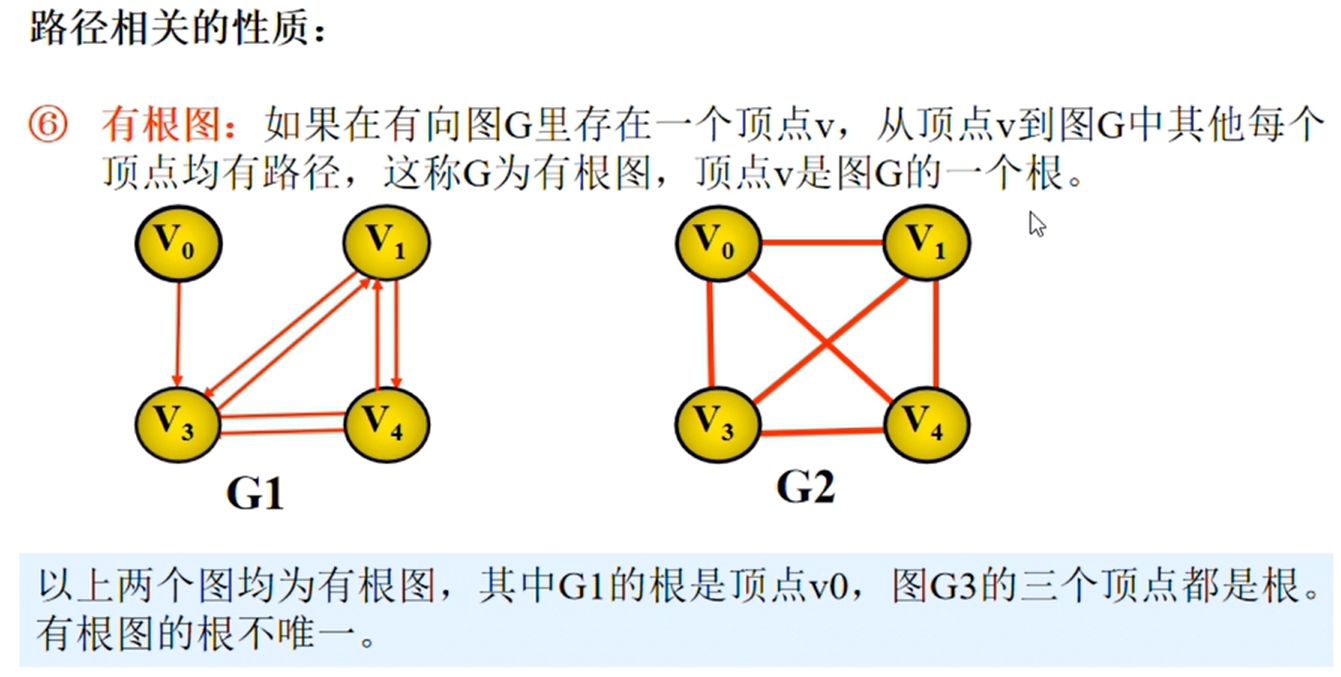
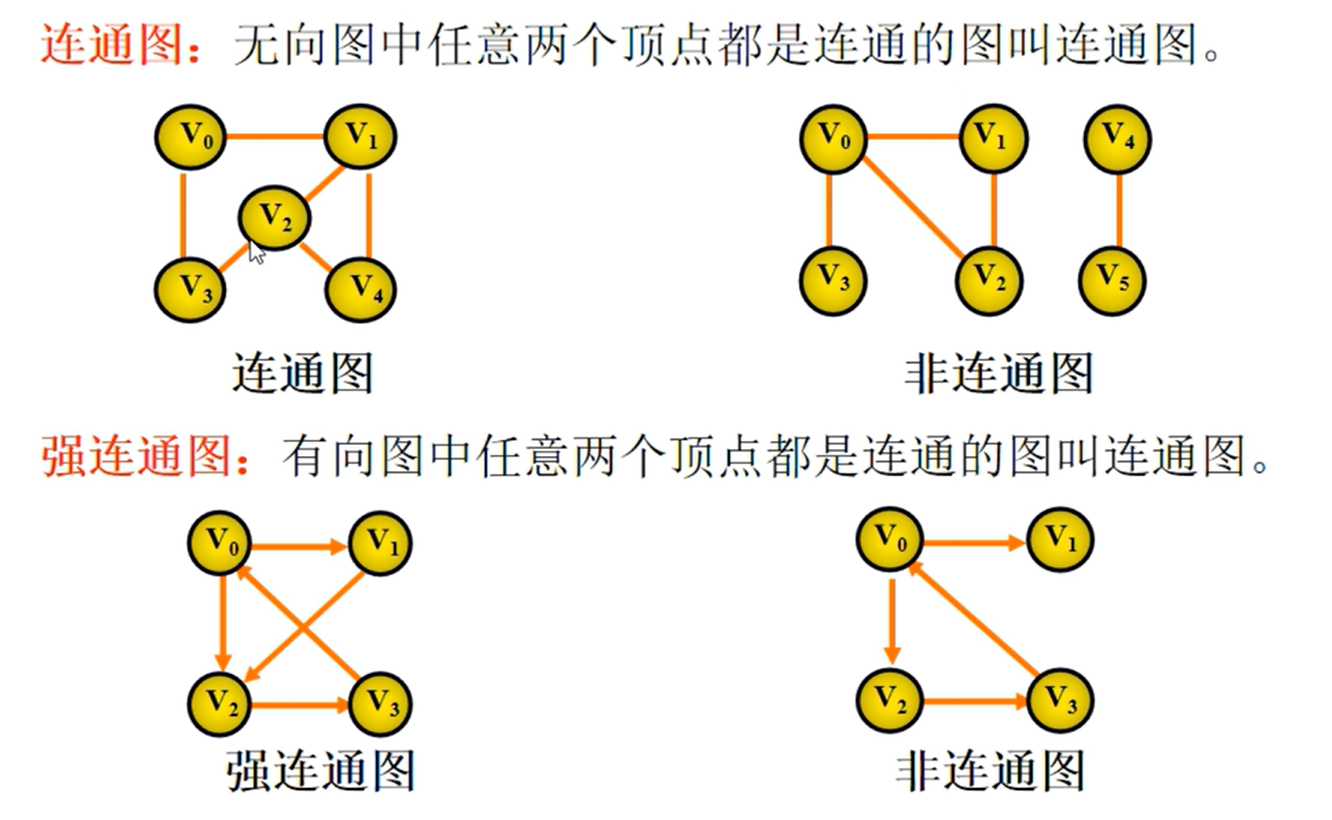
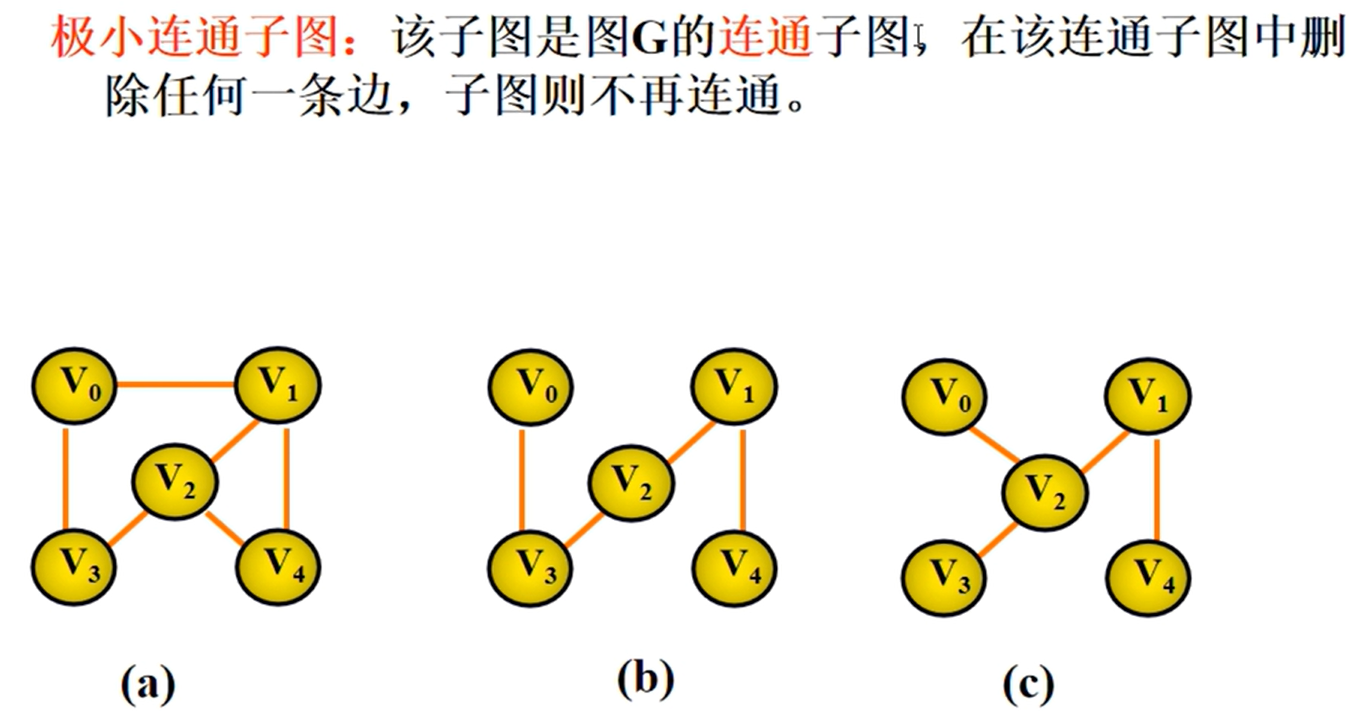
邻接矩阵
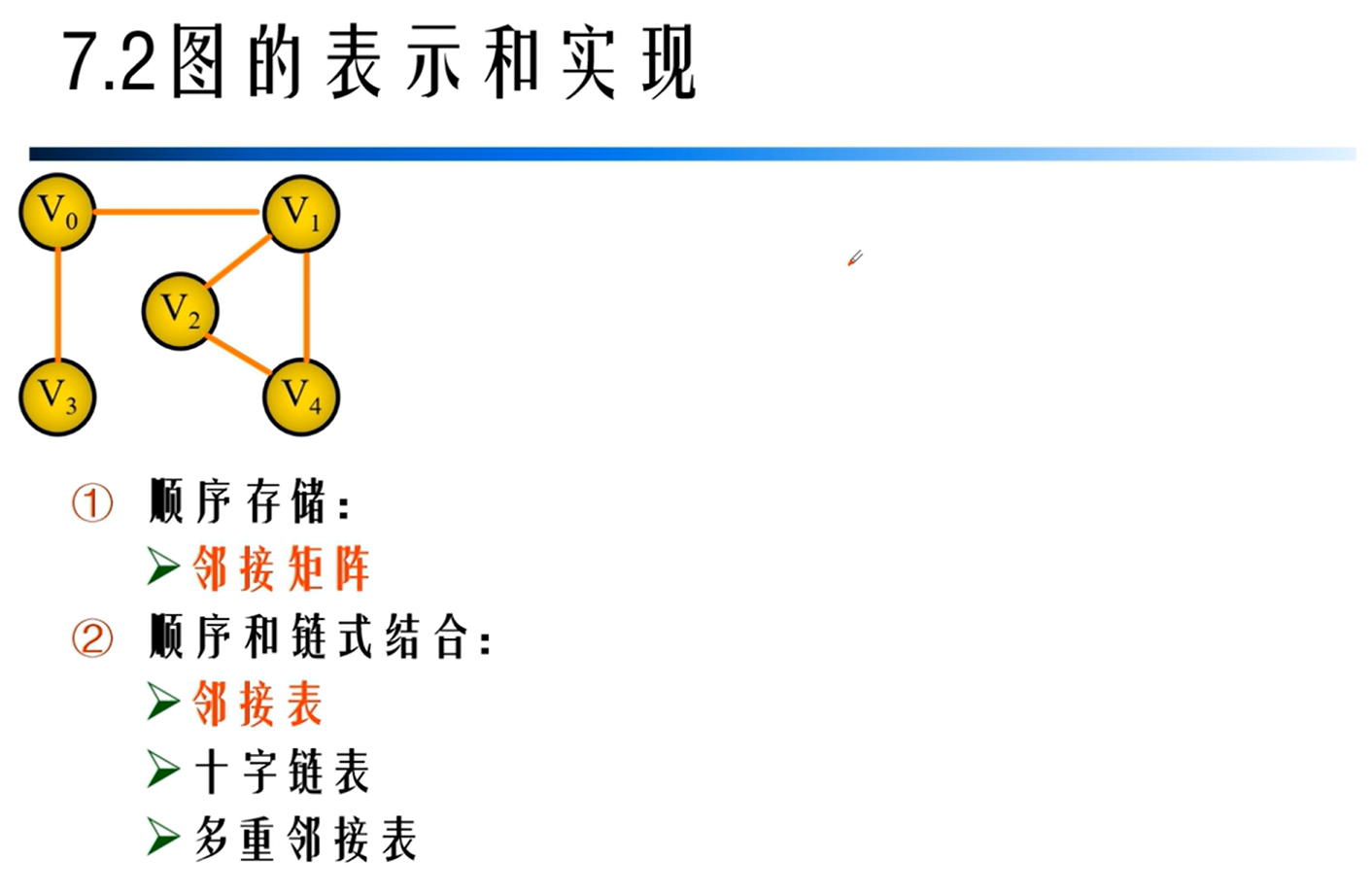

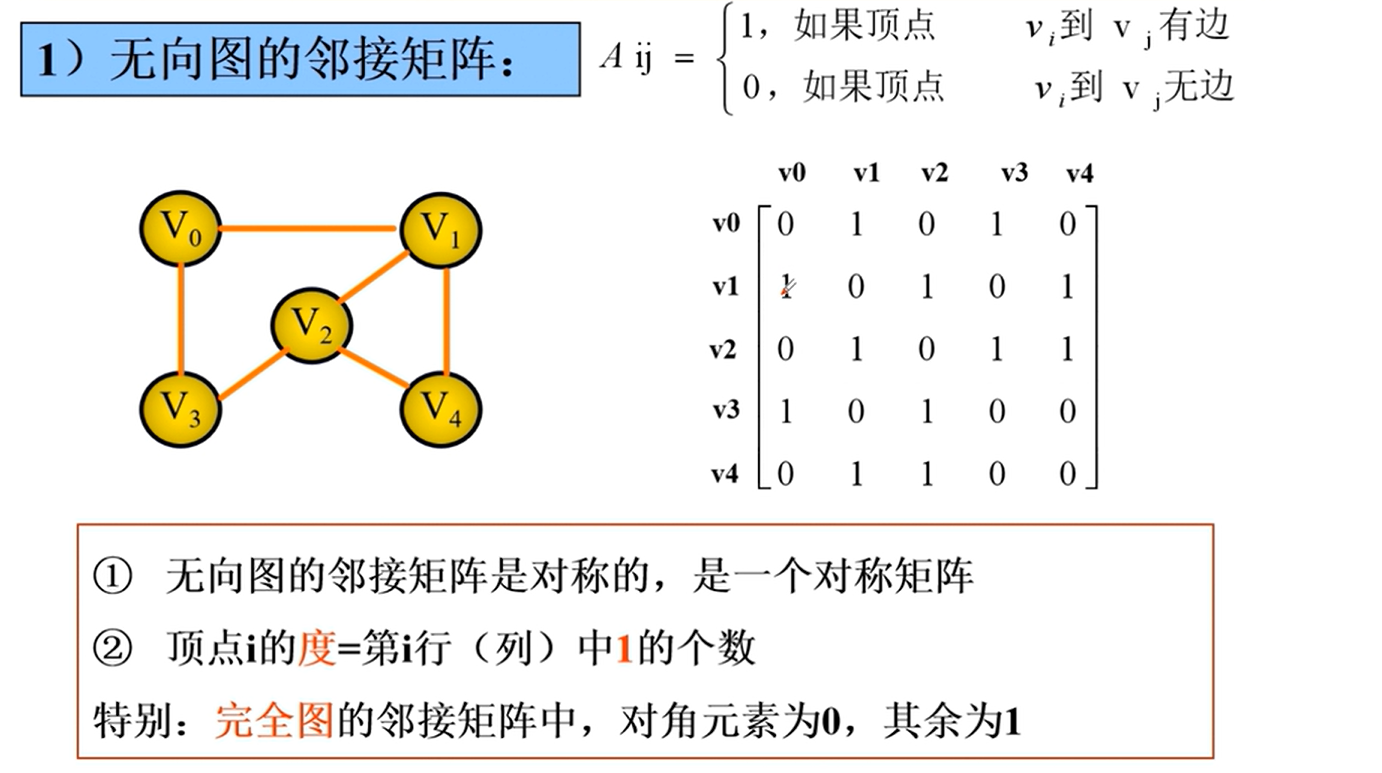
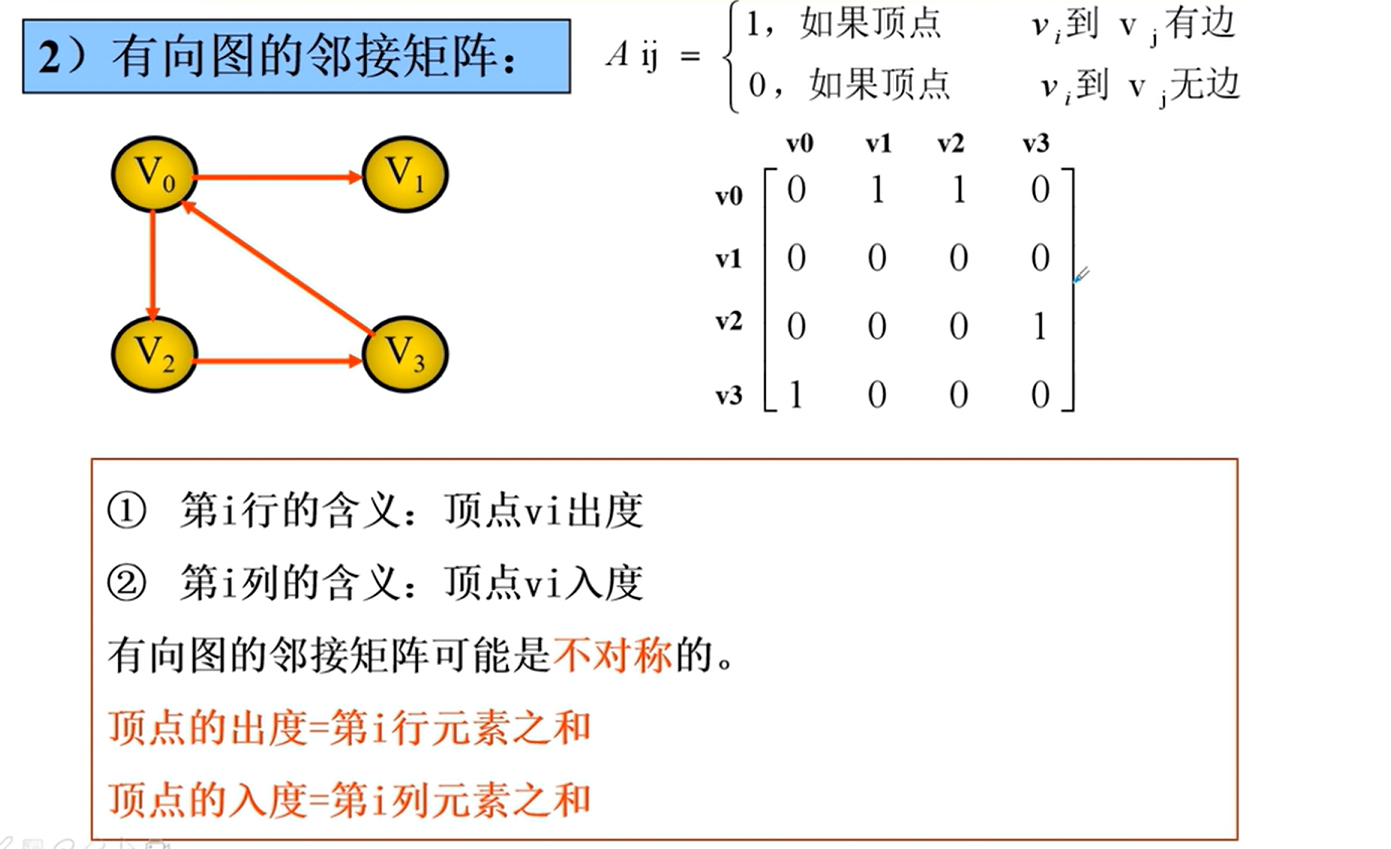
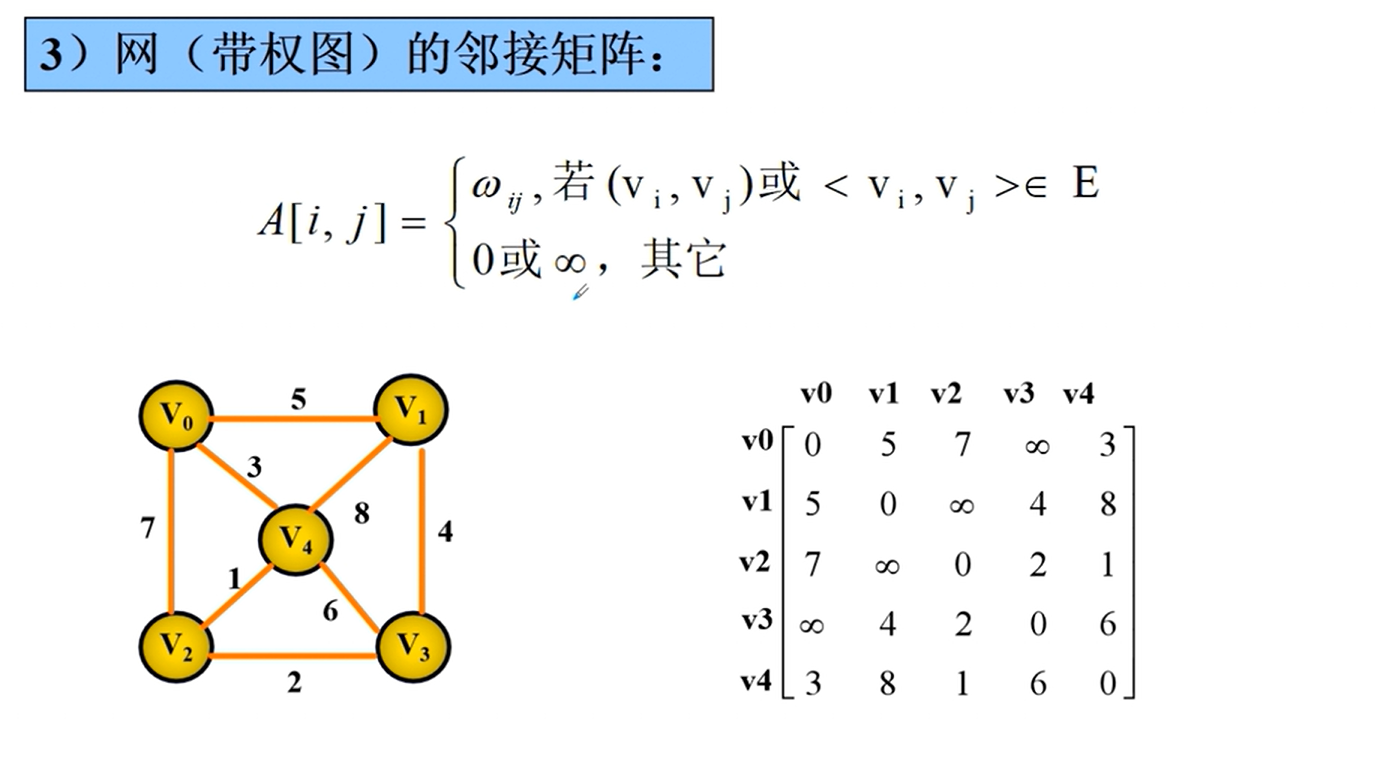
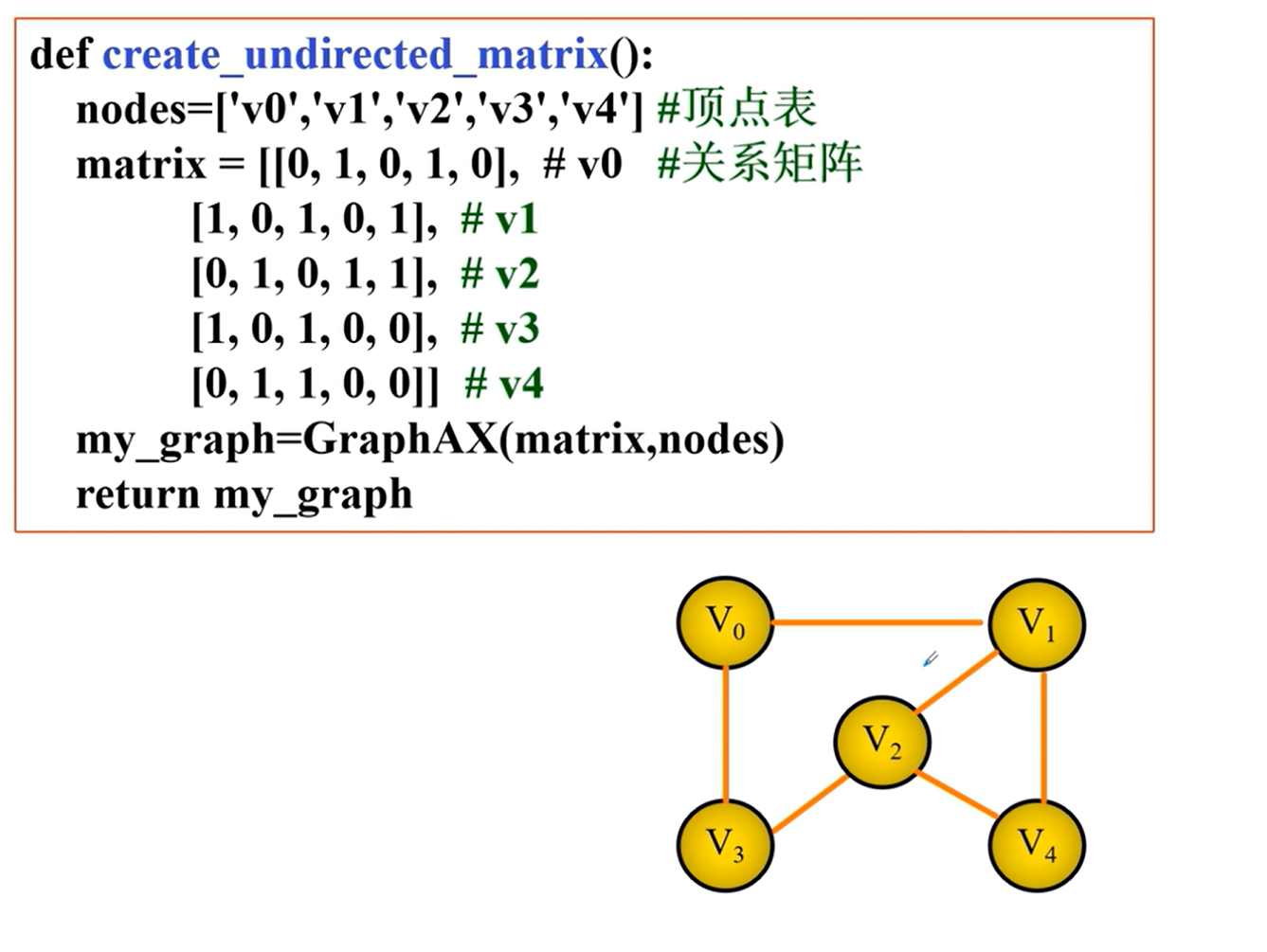
邻接矩阵的实现

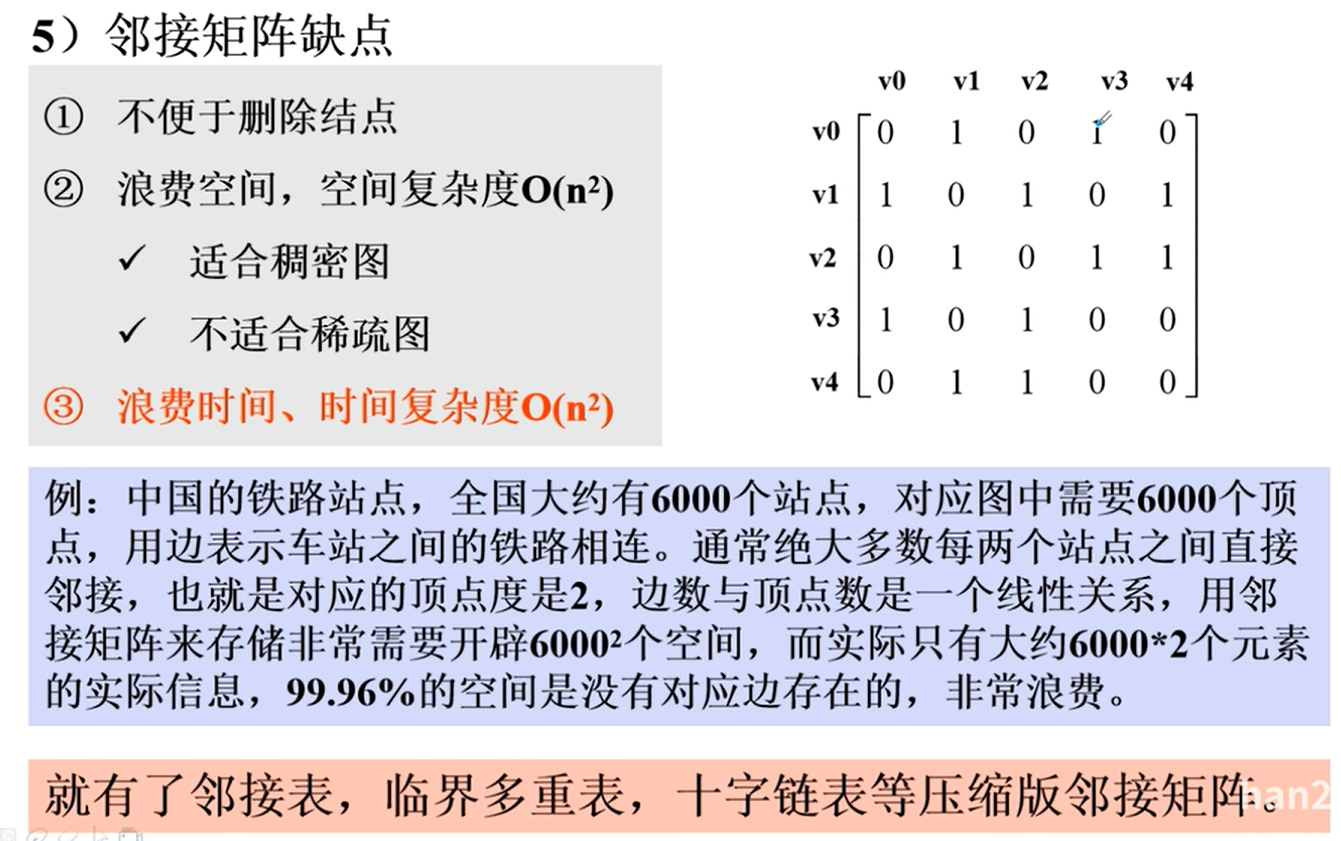
邻接矩阵的优劣


邻接表
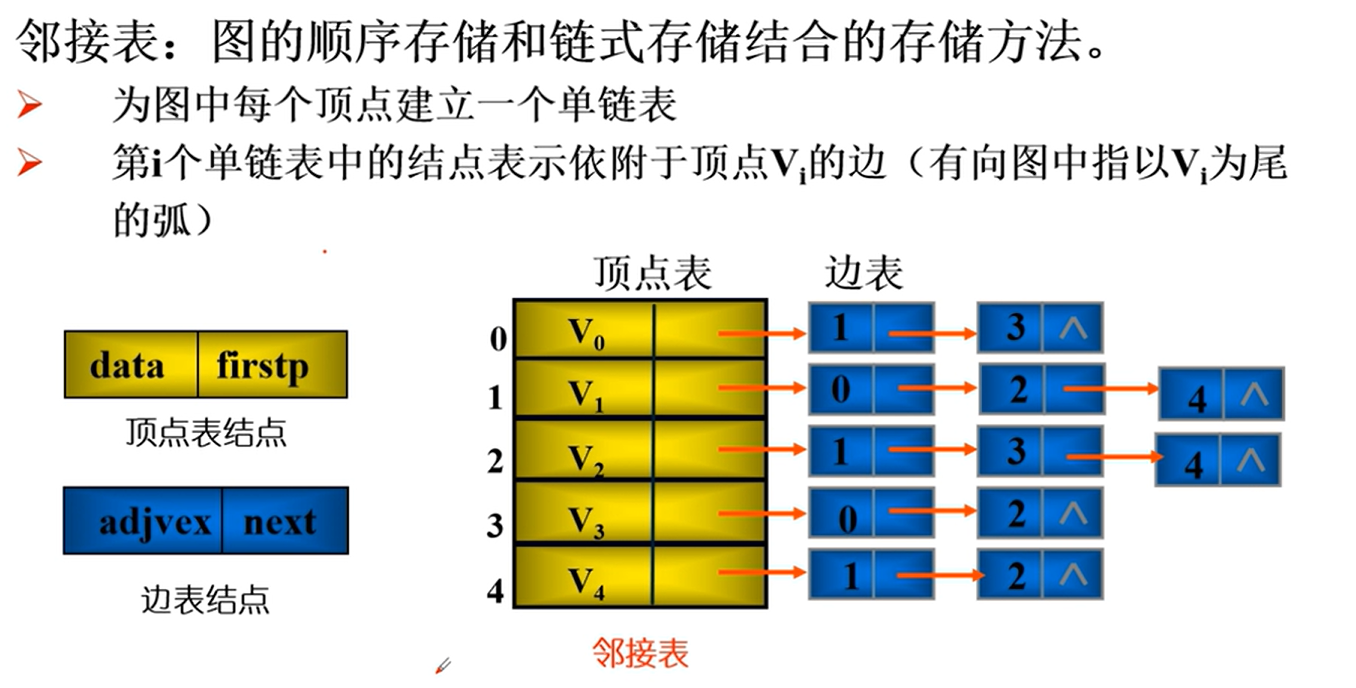
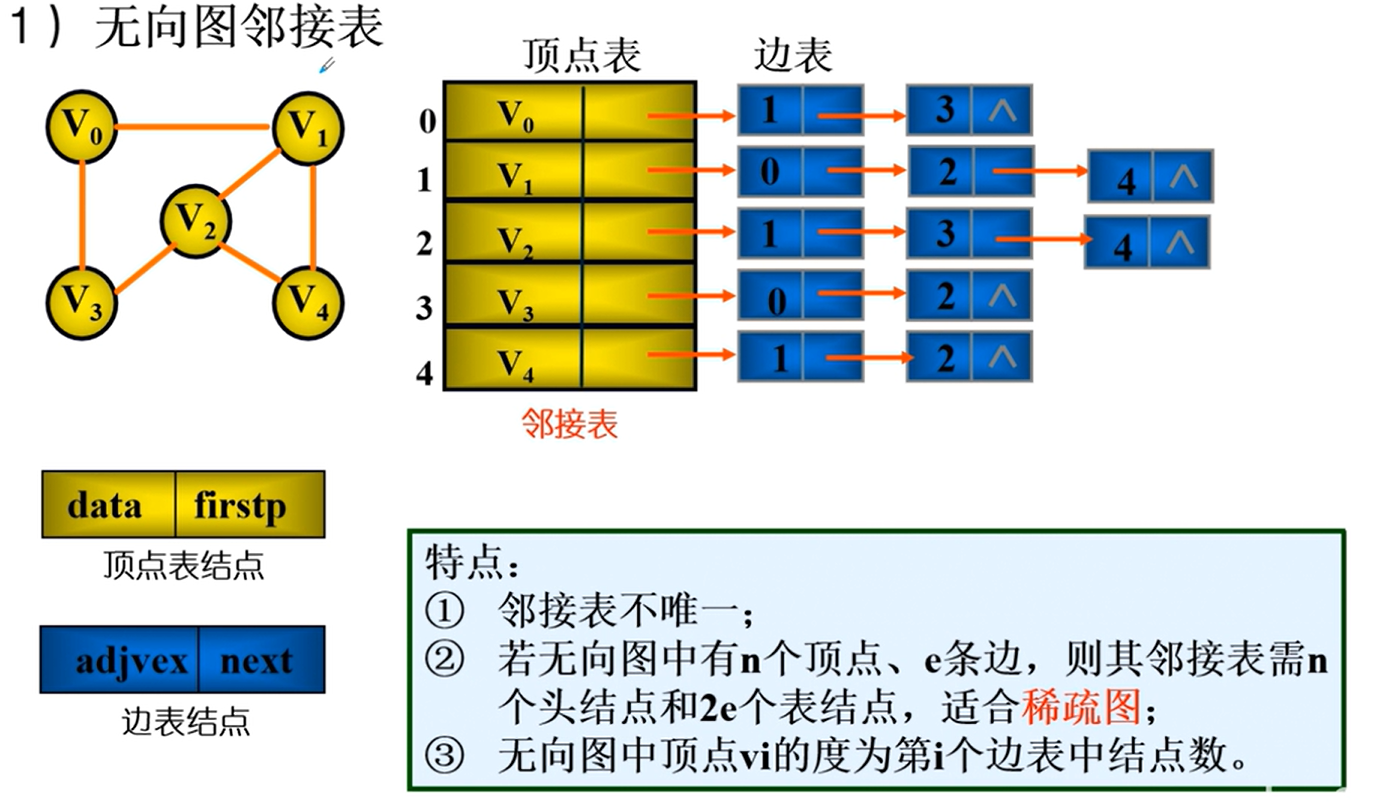
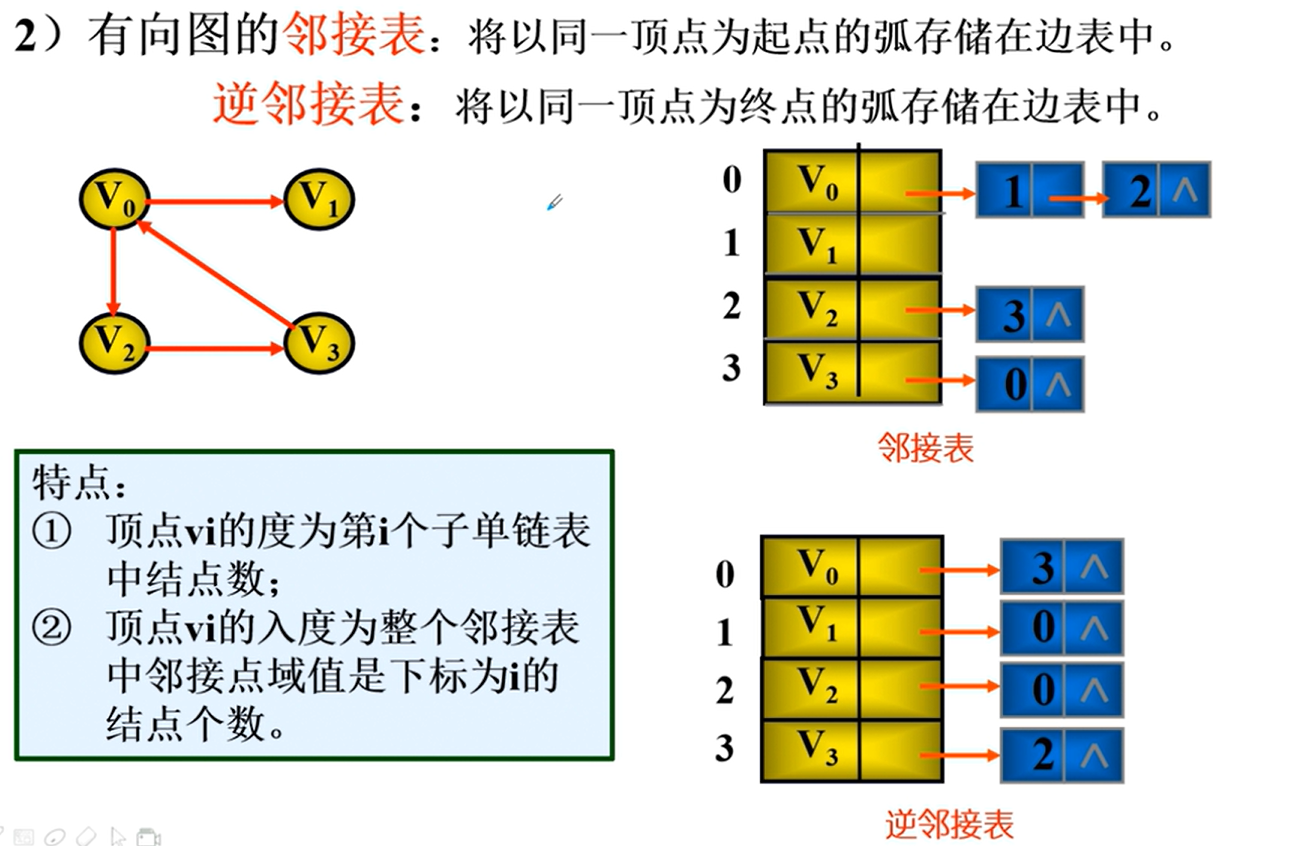
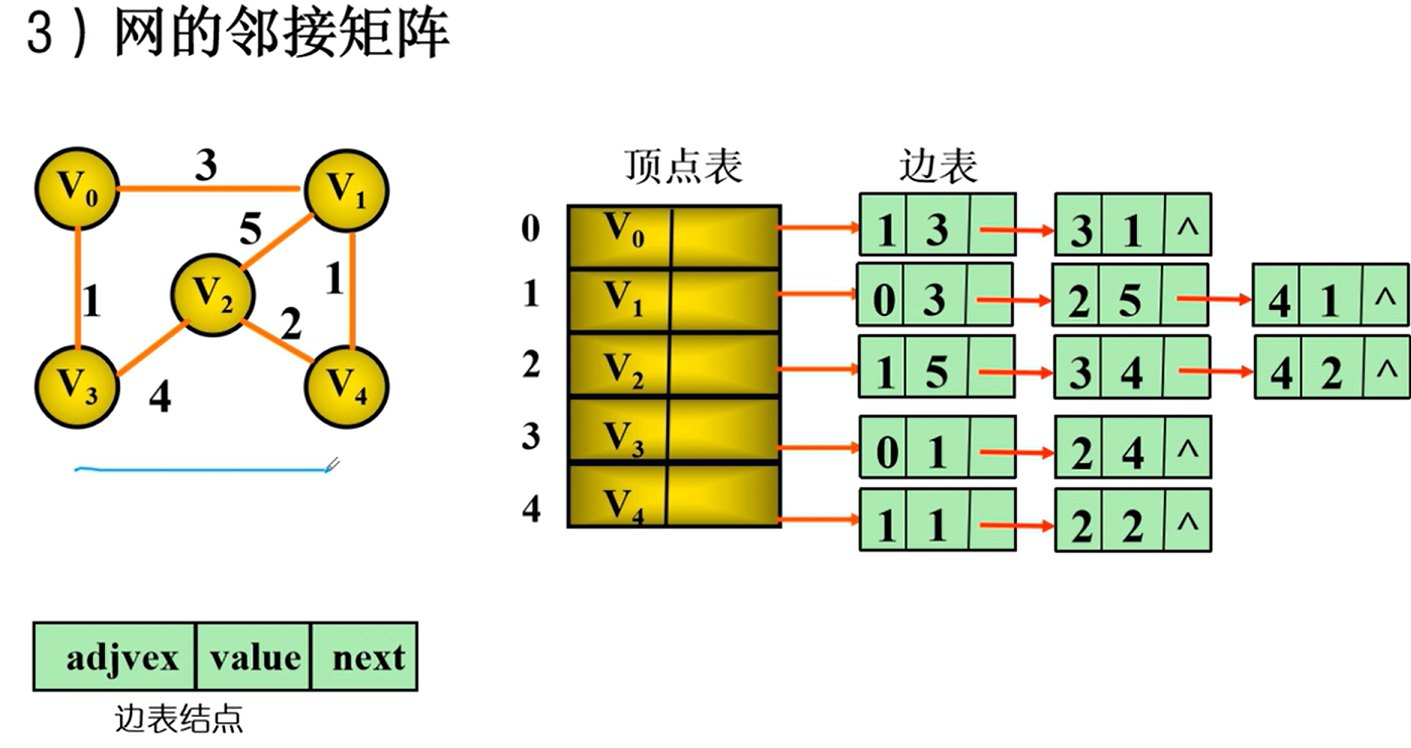
邻接表的实现



特点

库的调用

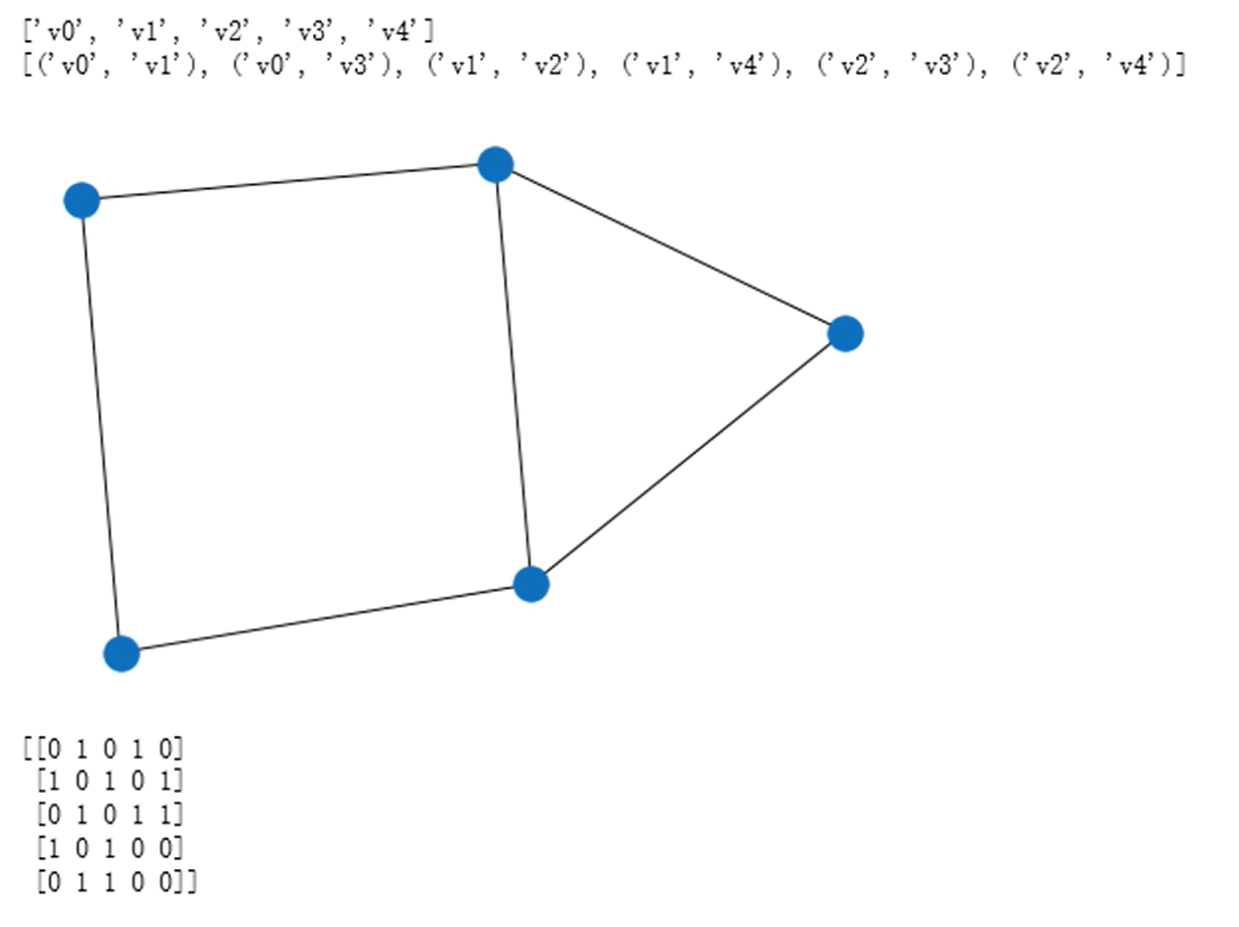
图的遍历
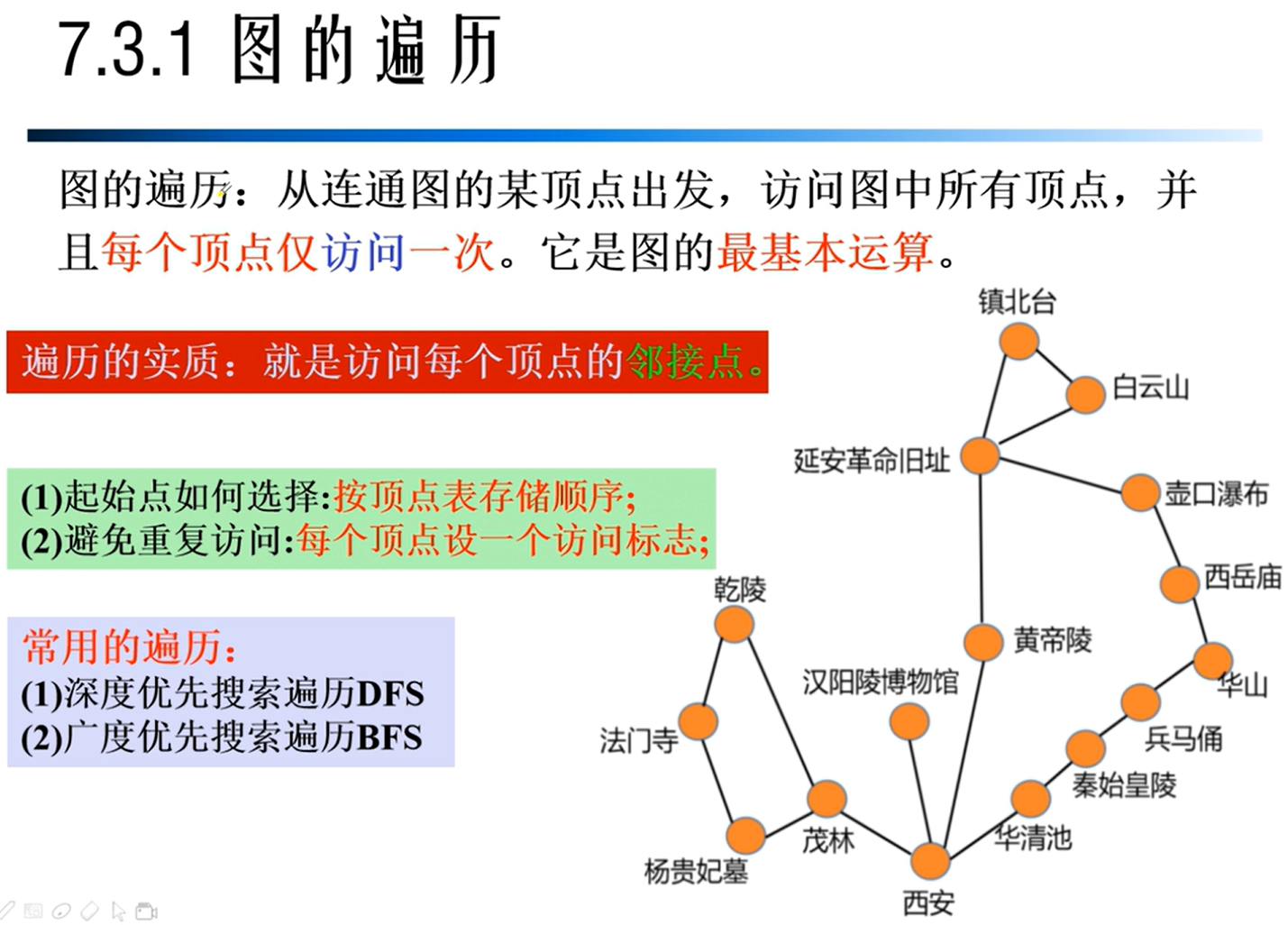
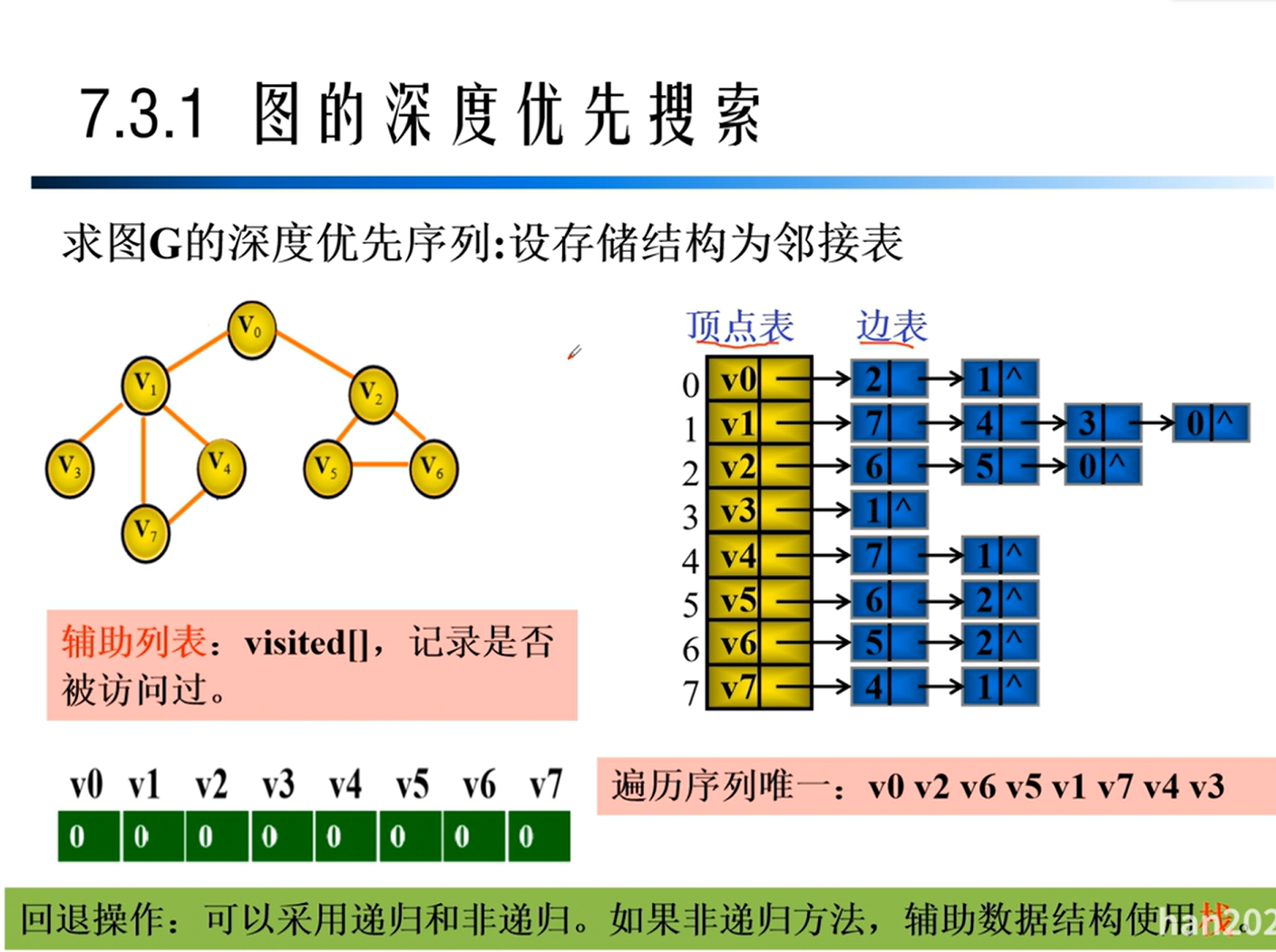
深度优先遍历


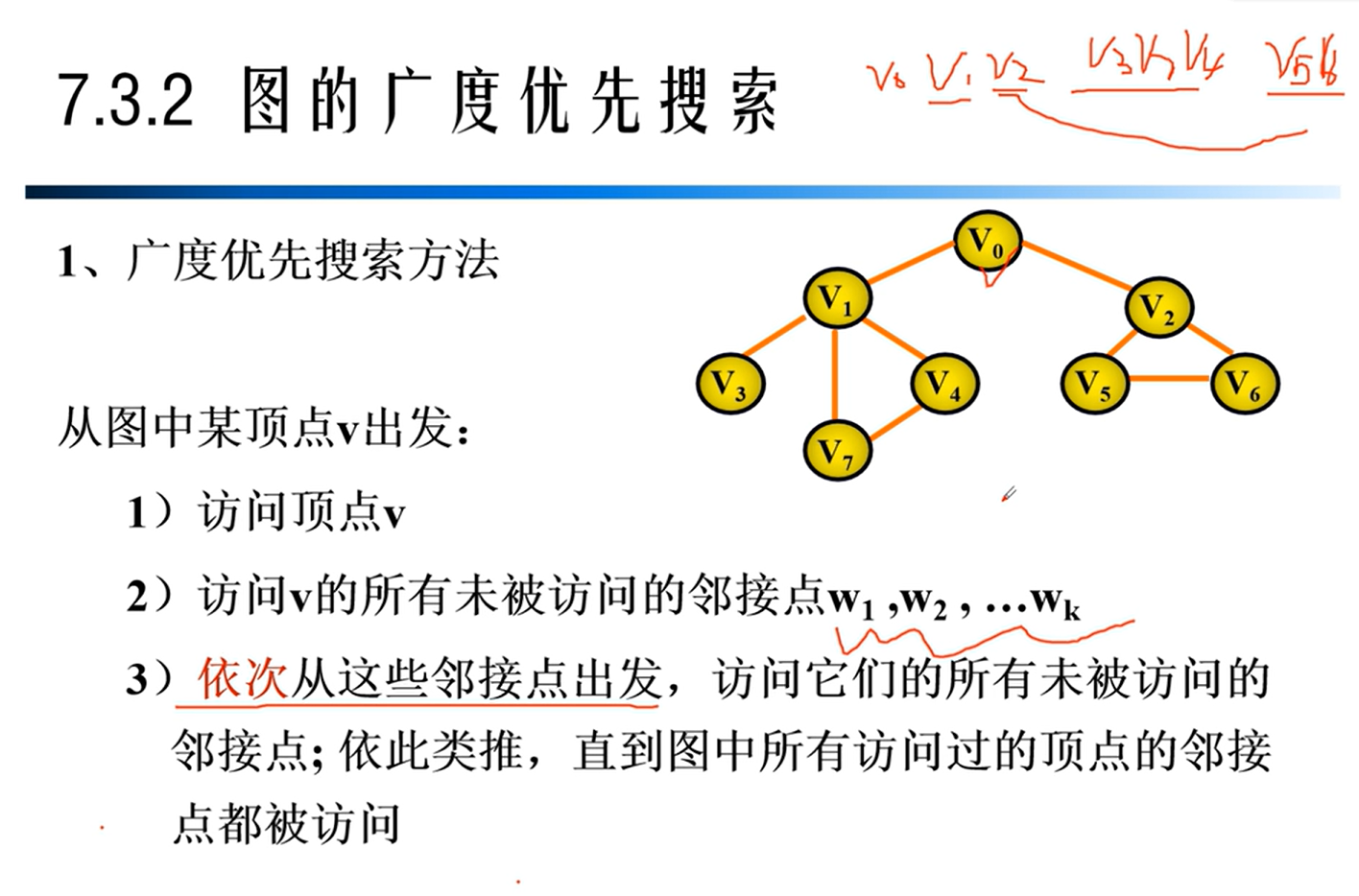
广度优先遍历
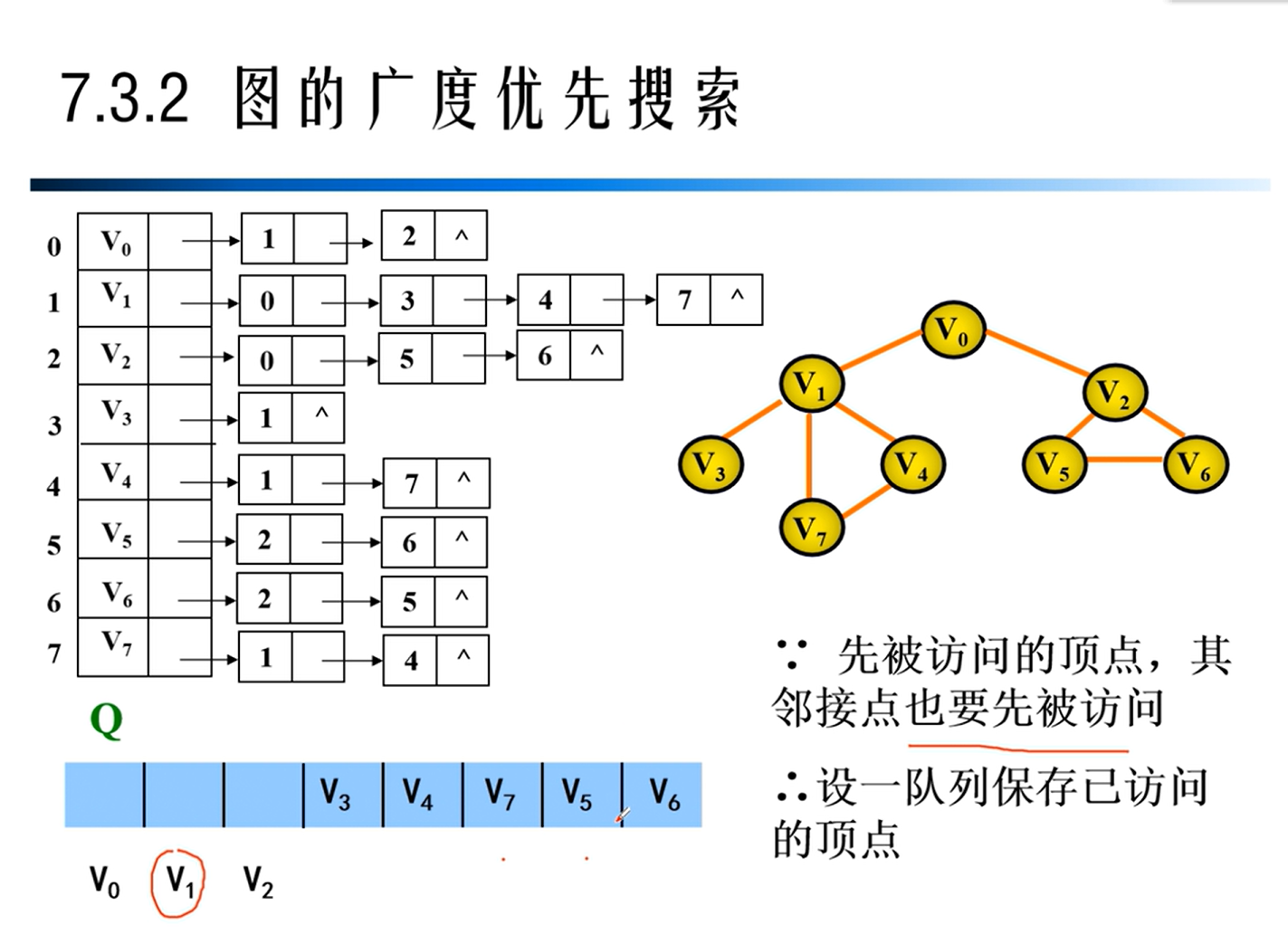

BFS与DFS算法比较

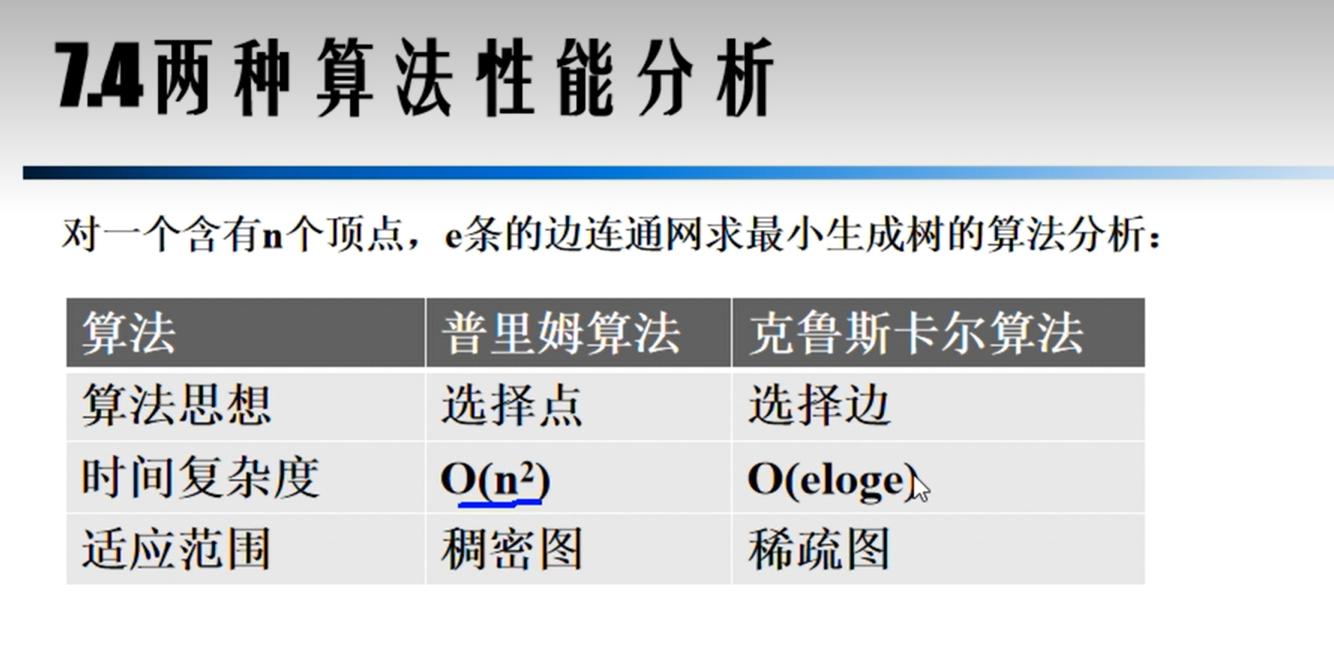
最小生成树
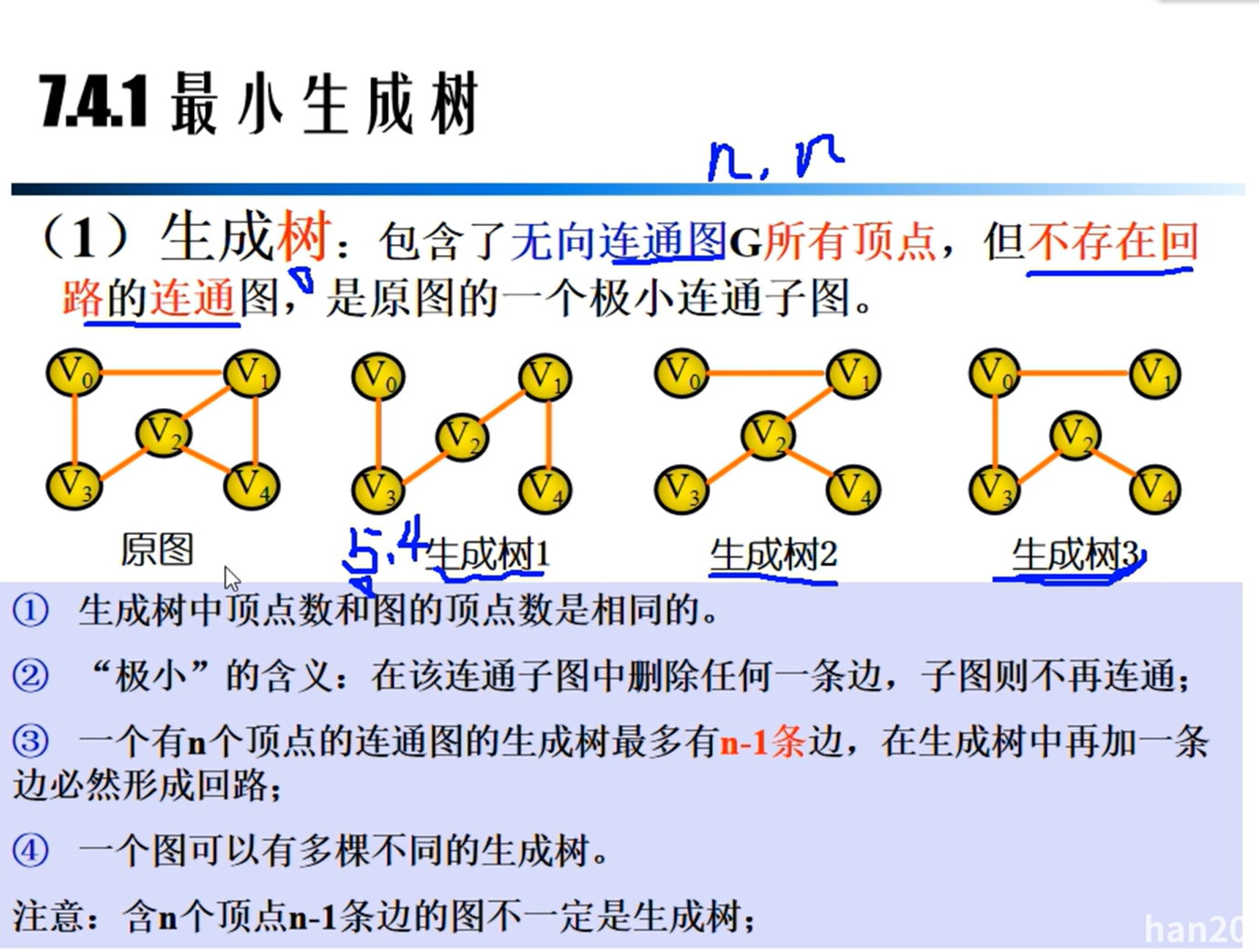
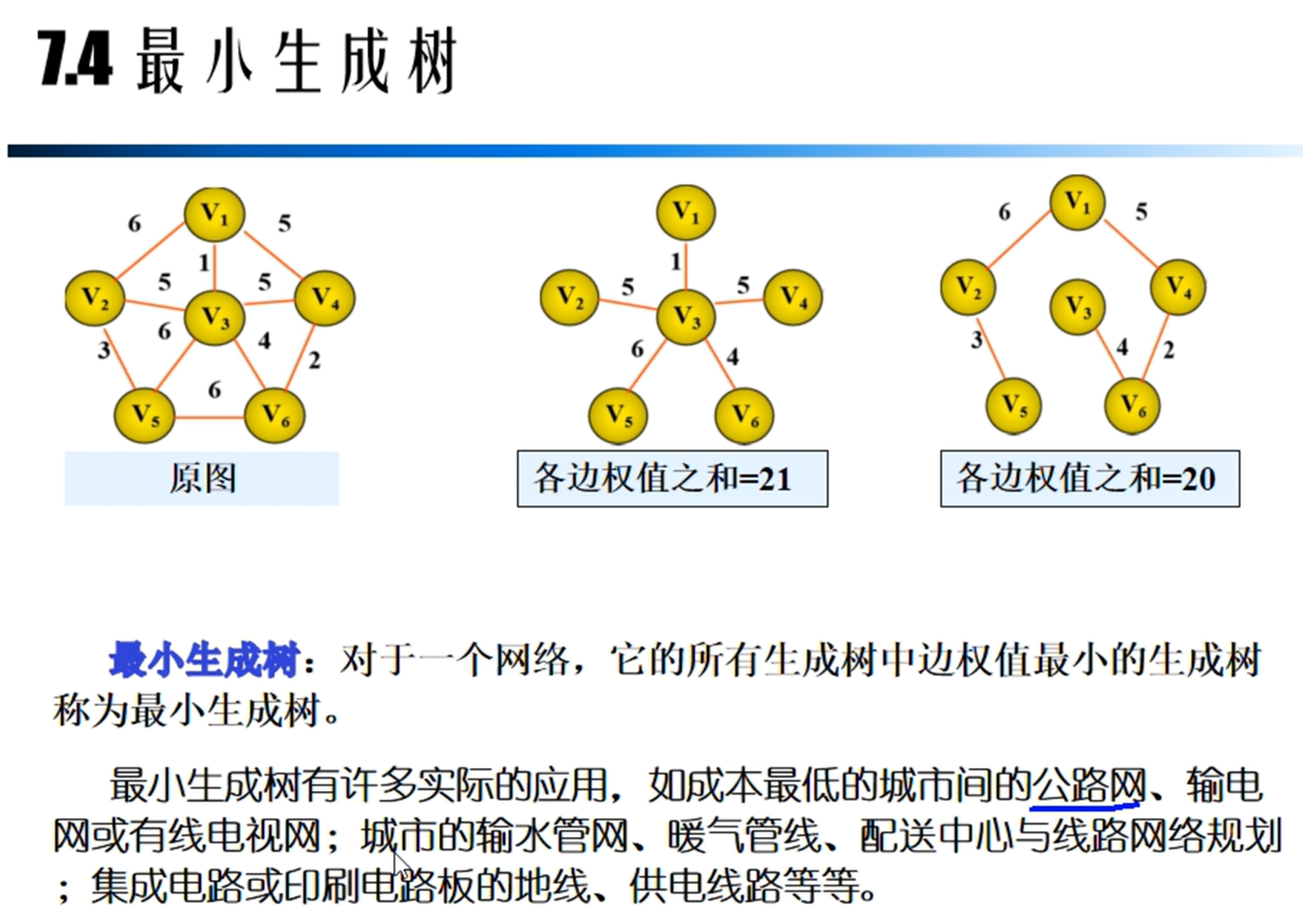
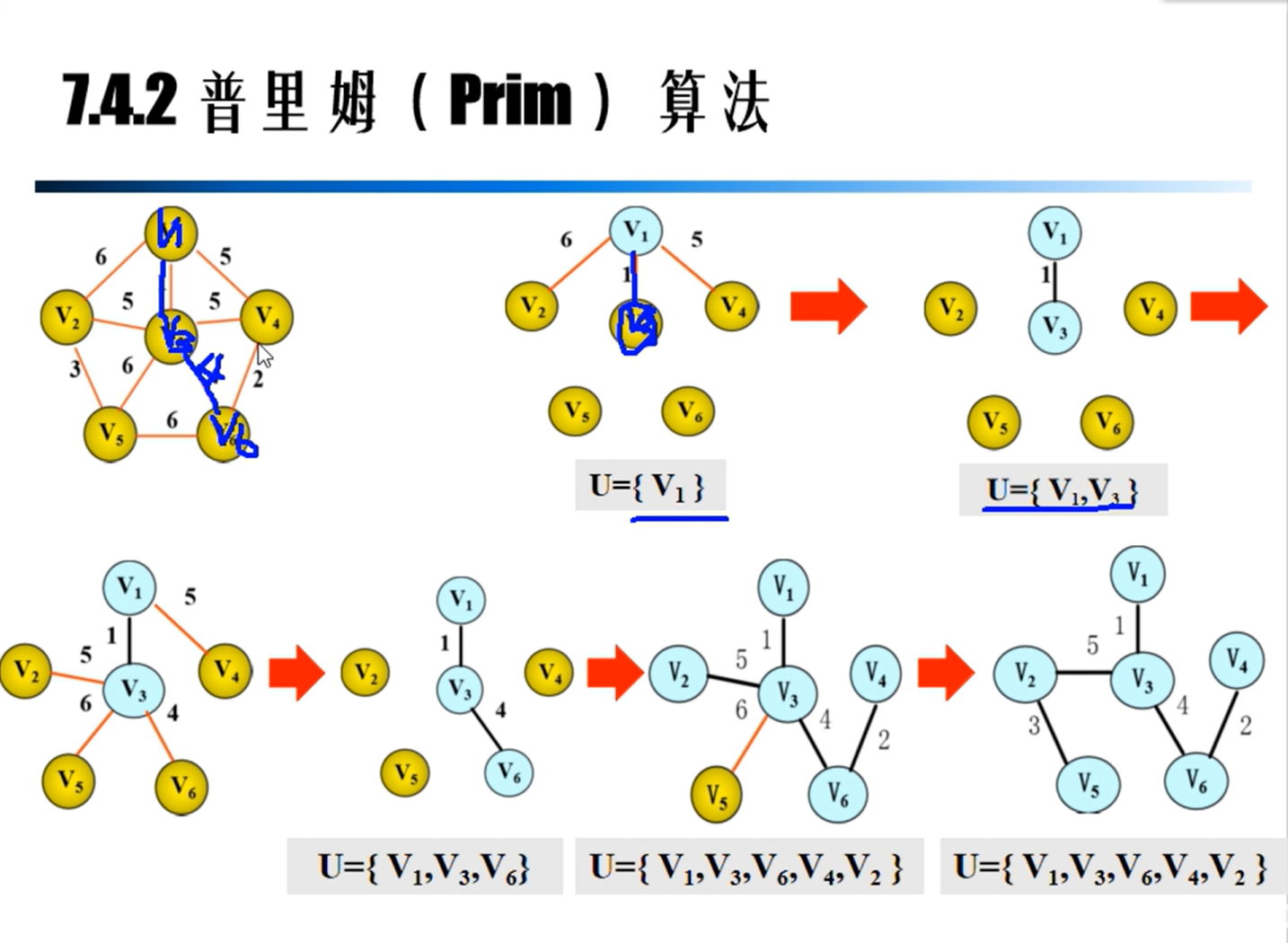
Prim算法
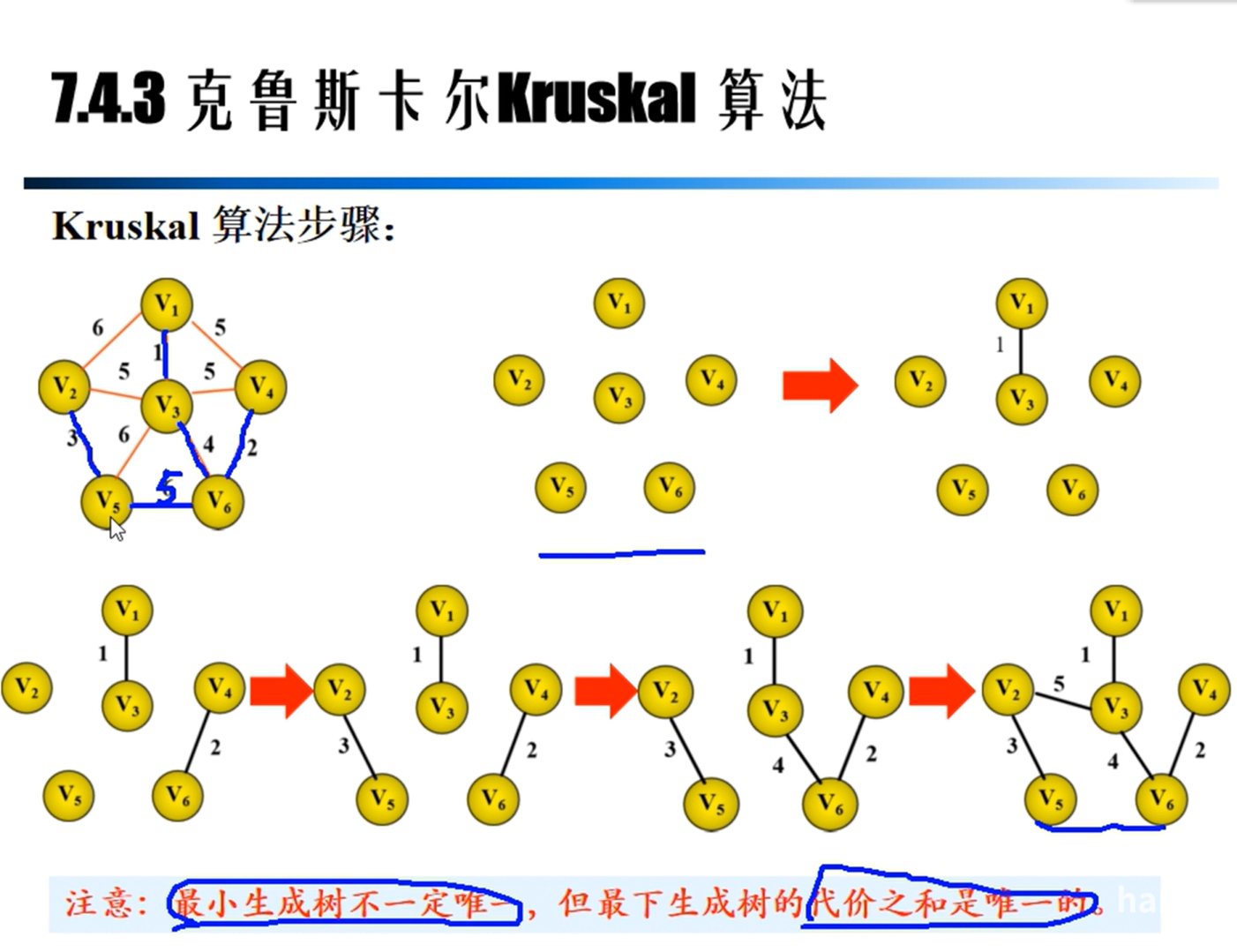
Kruskal算法
算法比较
最短路径
迪杰斯特拉算法

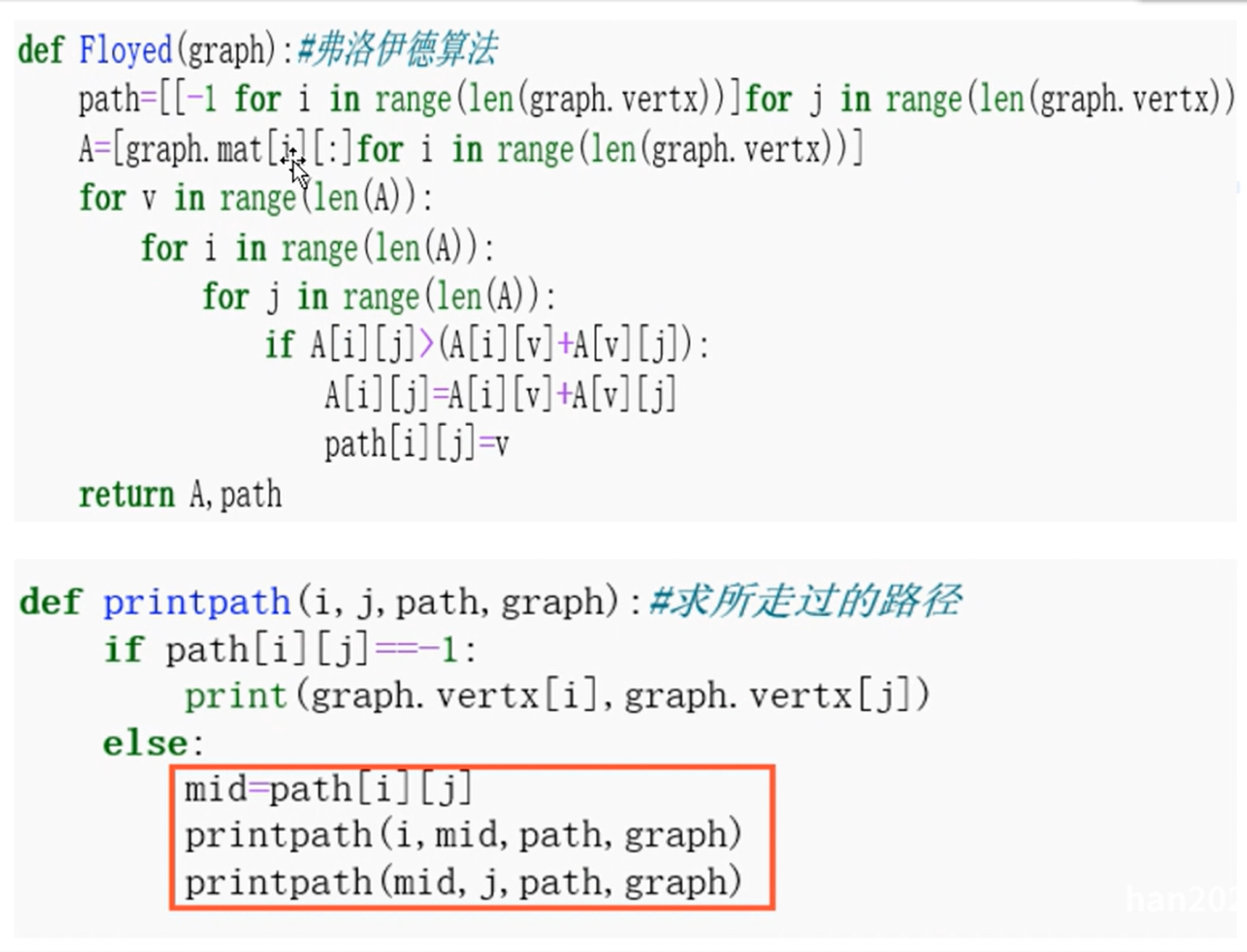
弗洛伊德算法
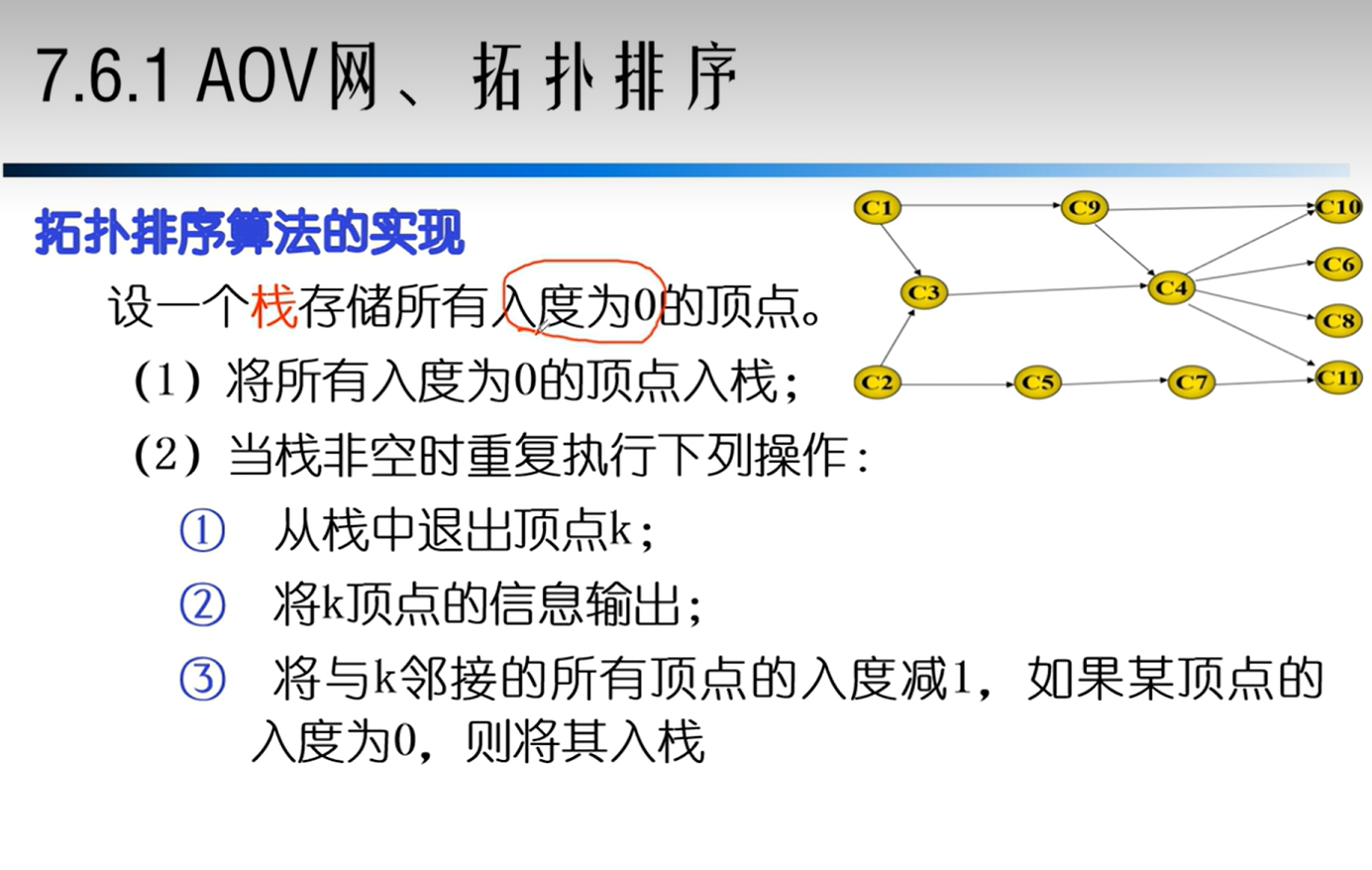
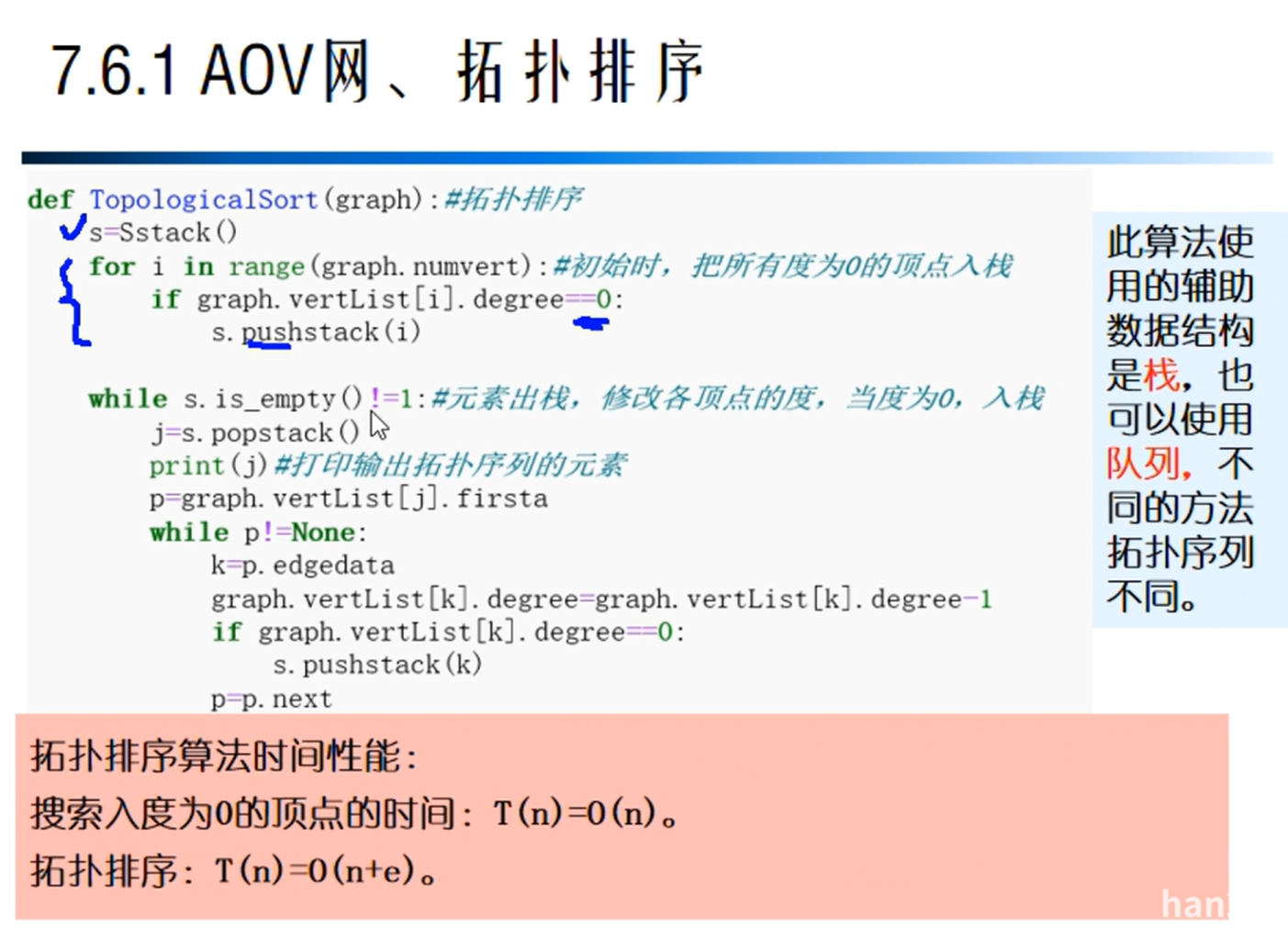
AOV网
拓扑排序

AOE网
关键路径

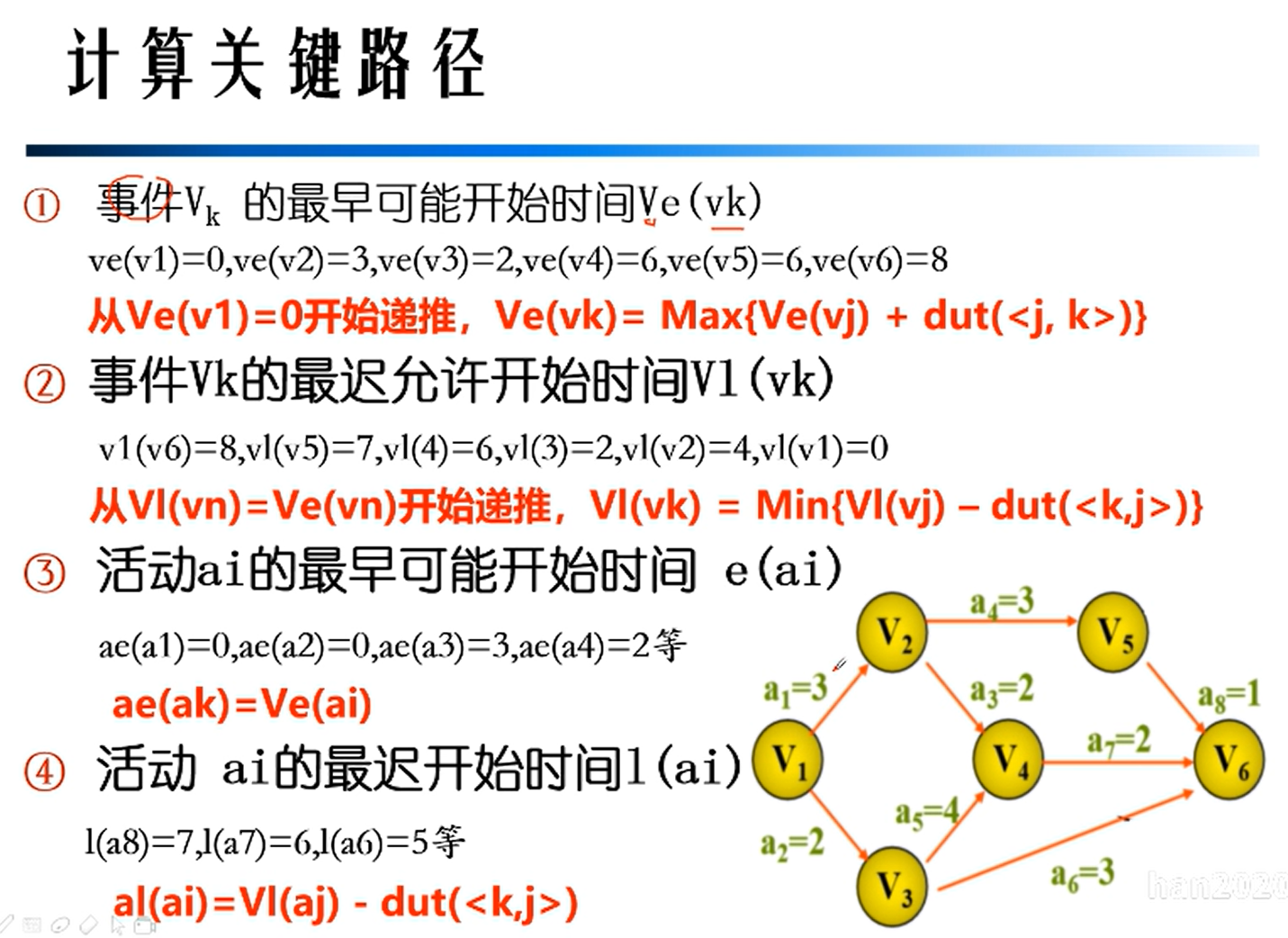


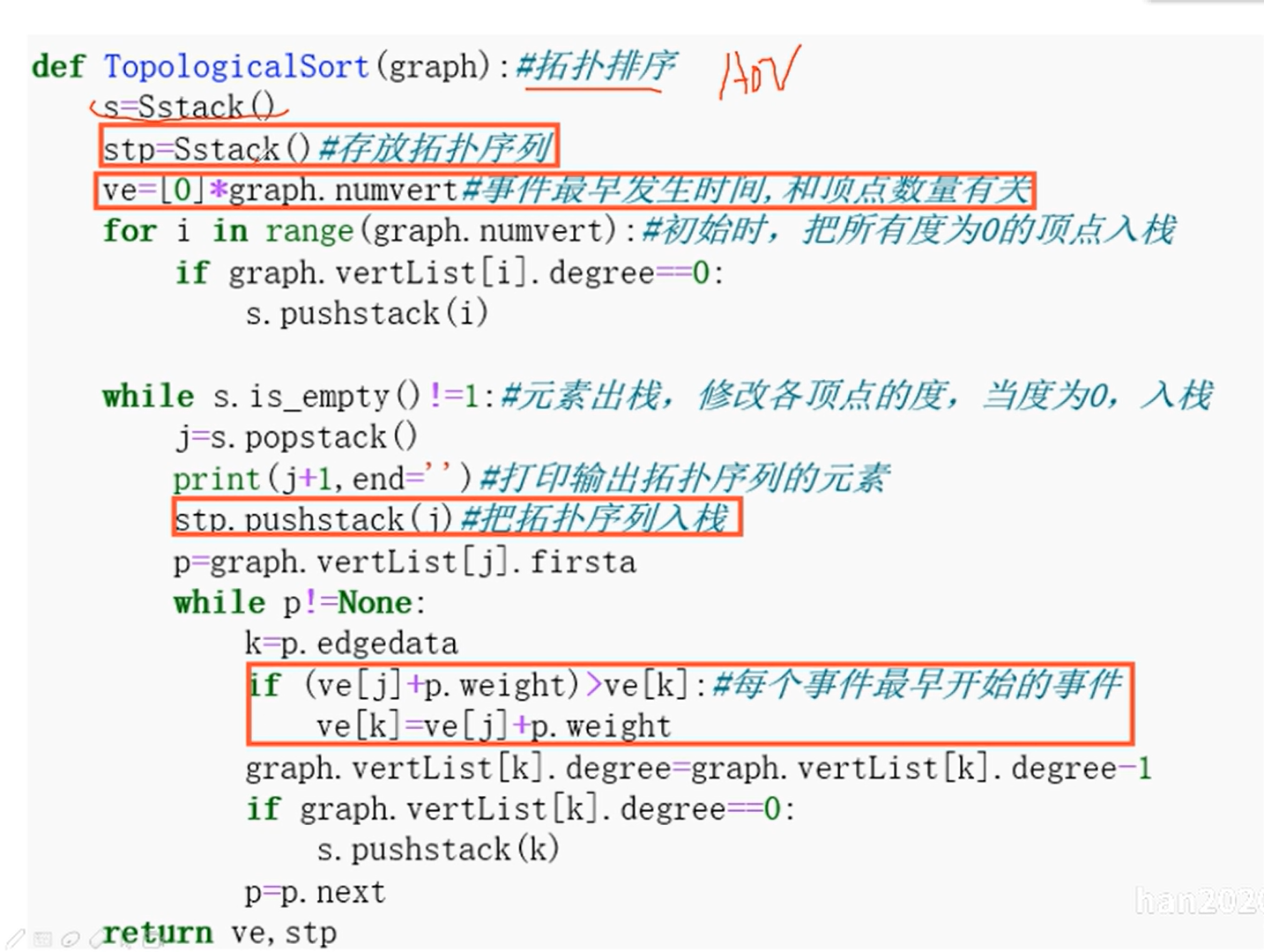
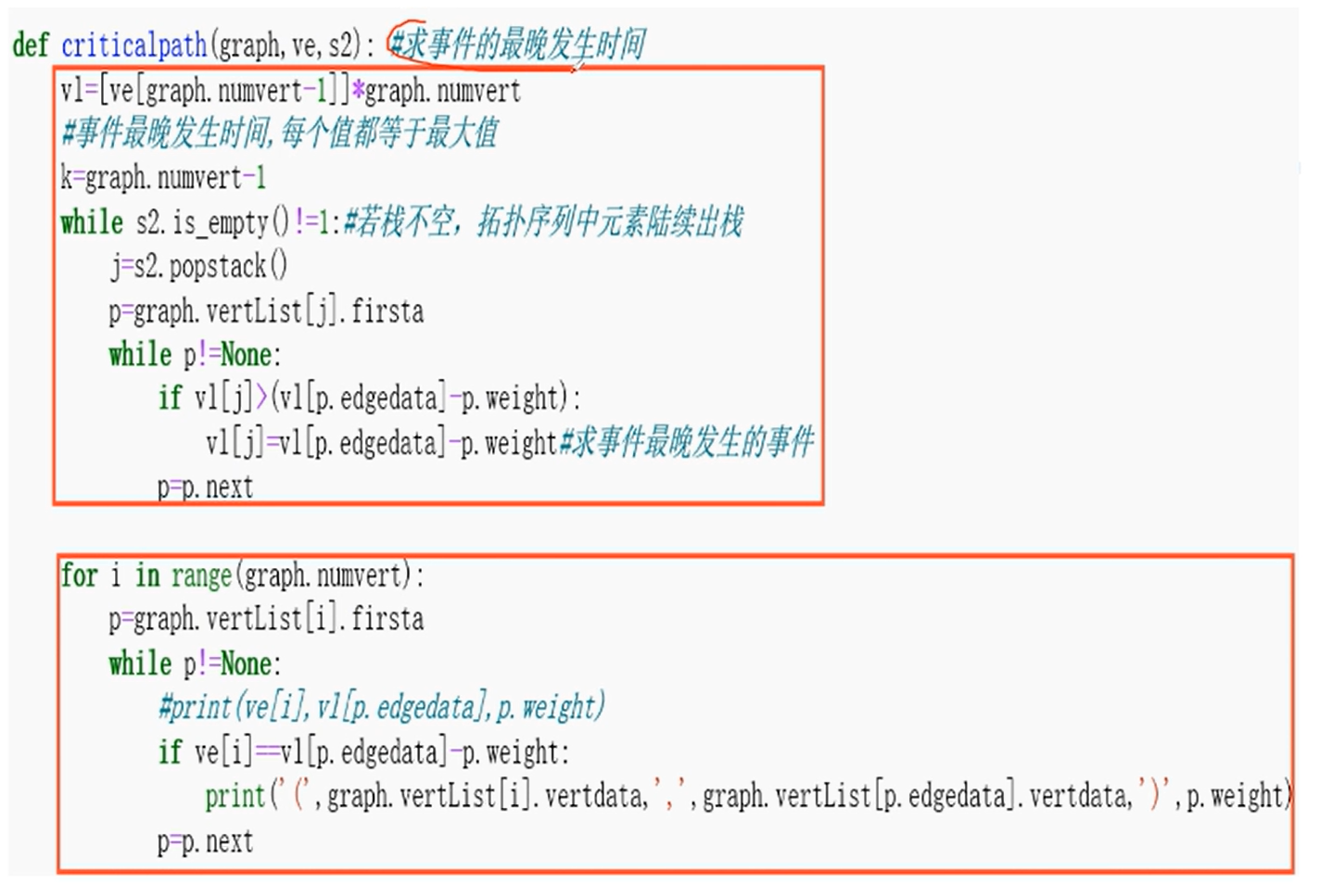
贪心算法

找零问题

代码
t = [100, 50, 20, 5, 1]
def change(t, n):
m = [0 for _ in range(len(t))]
for i, money in enumerate(t):
m[i] = n // money
n = n % money
return m, n
print(change(t, 376))
分数背包问题


代码
goods=[(60,10),(100,20),(120,30)]
goods.sort(key=lambda x:x[0]/x[1],reverse=True)
def fractional_backpack(goods,w):
m=[0 for _ in range(len(goods))]
total_v=0
for i,(prize,weight) in enumerate(goods):
if w>=weight:
m[i]=1
total_v+=prize
w-=weight
else:
m[i]=w/weight
total_v+=m[i]*prize
w=0
break
return total_v,m
print(fractional_backpack(goods,50))
拼接最大数字问题

代码
from functools import cmp_to_key
li = [32, 94, 128, 1286, 6, 71]
def xy_cmp(x, y):
if x + y < y + x:
return 1
elif x + y > y + x:
return -1
else:
return 0
def number_join(li):
li = list(map(str, li))
li.sort(key=cmp_to_key(xy_cmp))
return "".join(li)
print(number_join(li))
活动选择问题


代码
from operator import itemgetter
activities = [(1, 4), (3, 5), (0, 6), (5, 7), (5, 9), (3, 9), (6, 10), (8, 11), (8, 12), (2, 14), (12, 16)]
activities.sort(key=itemgetter(1, 0))
print(activities)
def activity_selection(a):
res = [a[0]]
for i in range(1, len(a)):
if a[i][0] >= res[-1][1]:
res.append(a[i])
return res
print(activity_selection(activities))
动态规划(DP算法)

钢管切割问题
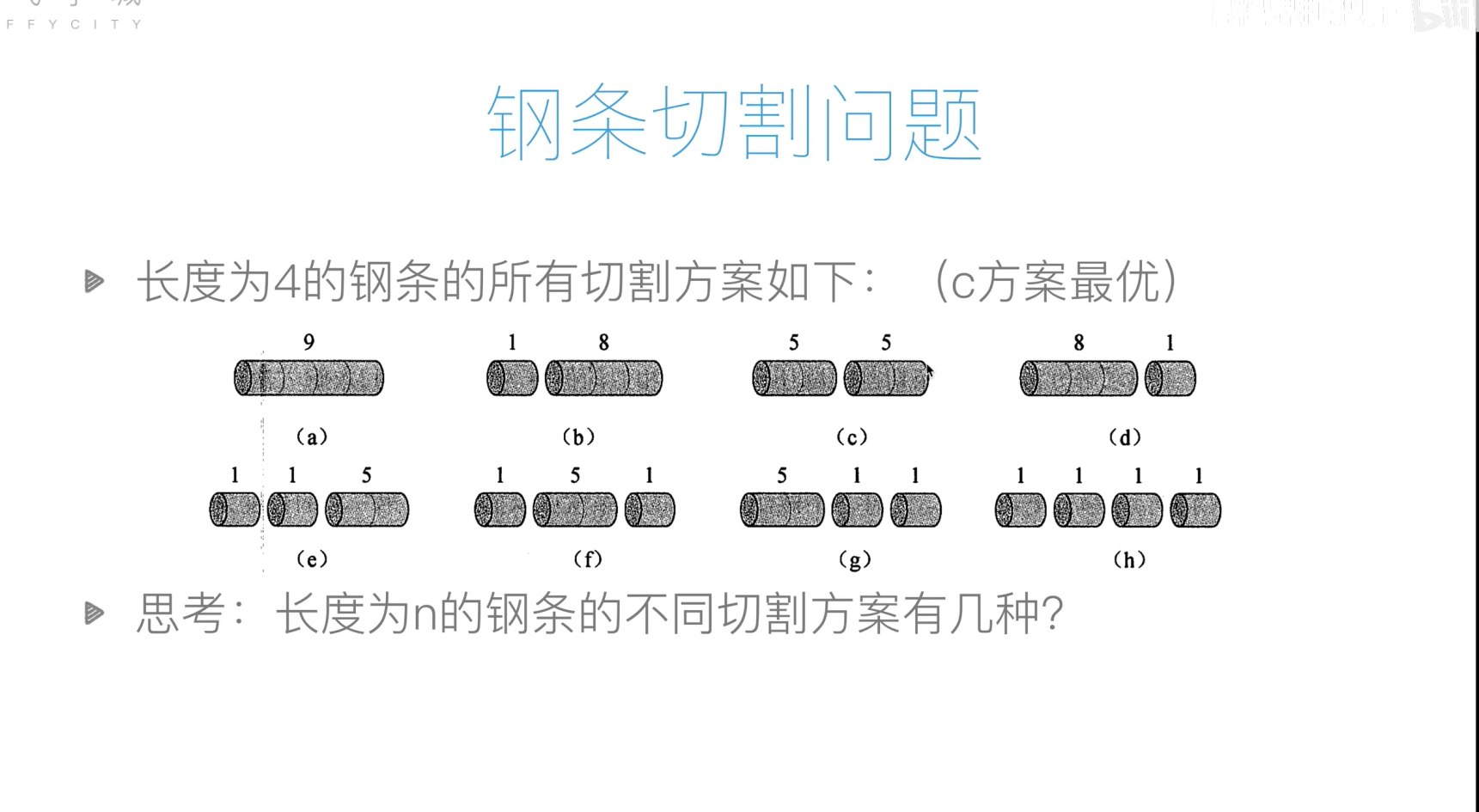
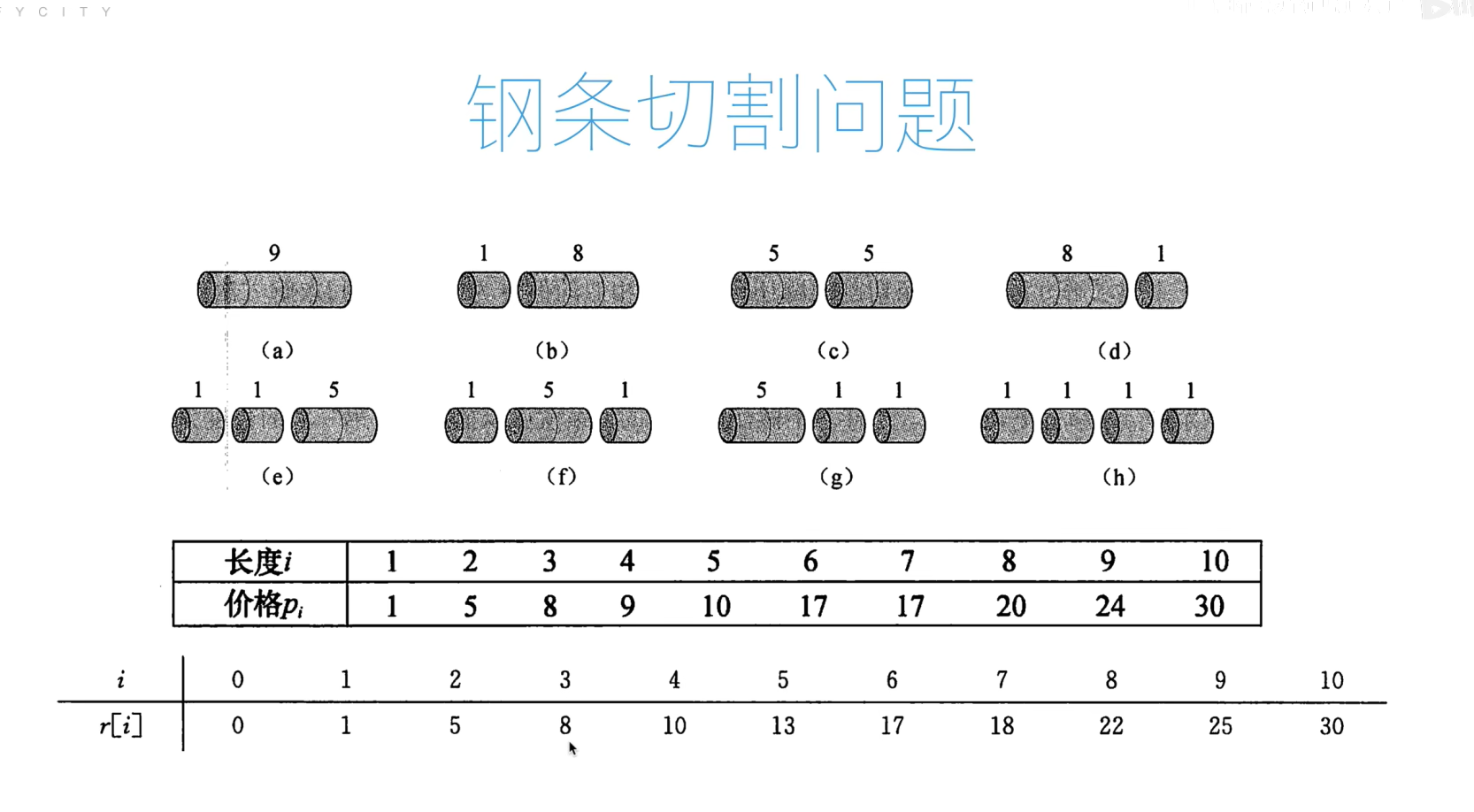




代码
def cut_rot_dp(p, n):
r = p.copy()
length = len(p)
solution_list = []
for i in range(1, length):
res = r[i]
solution = (i, 0)
for j in range(1, (i + 1) // 2 + 1):
res = max(res, r[j] + r[i - j])
if res == r[j] + r[i - j]:
solution = (j, i - j)
solution_list.append(solution)
r[i] = res
while n >= length:
res = 0
solution = tuple()
for j in range(1, (length + 1) // 2 + 1):
res = max(res, r[j] + r[length - j])
if res == r[j] + r[length - j]:
solution = (j, length - j)
solution_list.append(solution)
r.append(res)
length += 1
solution_list.insert(0, tuple())
return r[-1], solution_list
def find(li):
queue = [li[-1]]
res = []
while queue:
tmp = queue.pop(0)
if tmp[1] == 0:
res.append(tmp)
else:
queue.append(li[tmp[0]])
queue.append(li[tmp[1]])
return res
def cut_rot(p, n):
r, solution_list = cut_rot_dp(p, n)
res = find(solution_list)
return r, res
p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]
print(cut_rot(p,49))
最长公共子序列问题


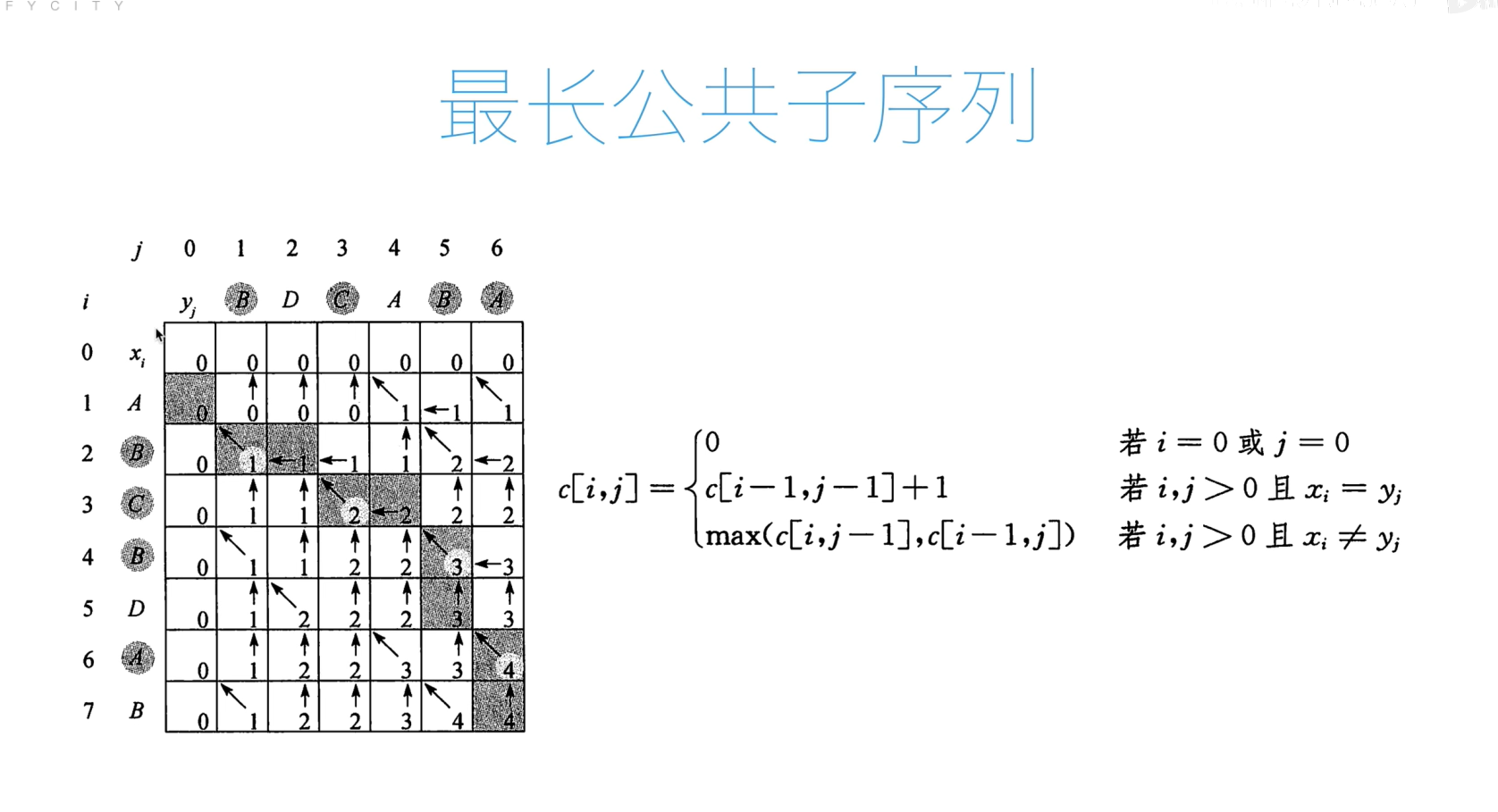
代码
def lcs(x, y):
m = len(x)
n = len(y)
c = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
b = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
for i in range(1, m + 1):
for j in range(1, n + 1):
if x[i - 1] == y[j - 1]:
c[i][j] = c[i - 1][j - 1] + 1
b[i][j] = 1
elif c[i - 1][j] > c[i][j - 1]:
c[i][j] = c[i - 1][j]
b[i][j] = 2
else:
c[i][j] = c[i][j - 1]
b[i][j] = 3
return c[m][n], b
def lcs_trackback(x, y):
c, b = lcs(x, y)
i = len(x)
j = len(y)
res = []
while i > 0 and j > 0:
if b[i][j] == 1:
res.append(x[i - 1])
i -= 1
j -= 1
elif b[i][j] == 2:
i -= 1
else:
j -= 1
return ''.join(reversed(res))
print(lcs_trackback("ABCBDAB","BDCABA"))
欧几里得算法(求最大公约数)

def gcd(a, b):
if b == 0:
return a
else:
return gcd(b, a % b)
def gcd2(a, b):
while b > 0:
r = a % b
a = b
b = r
return a
print(gcd(12, 16))
print(gcd2(12, 16))
应用

class Fraction:
def __init__(self,a,b):
self.molecule=a
self.denominator=b
x=self.gcd(a,b)
self.molecule/=x
self.denominator/=x
def gcd(self,a,b):
while b > 0:
r = a % b
a = b
b = r
return a
def __add__(self, other):
denominator=self.zgs(self.denominator,other.denominator)
molecule=self.molecule*denominator/self.denominator+other.molecule*denominator/other.denominator
return Fraction(molecule,denominator)
def zgs(self,a,b):
x=self.gcd(a,b)
return a*b/x
def __str__(self):
return "%d/%d"%(self.molecule,self.denominator)
num1=Fraction(2,10)
print(num1)
num2=Fraction(1,6)
print(num1+num2)
RSA加密算法

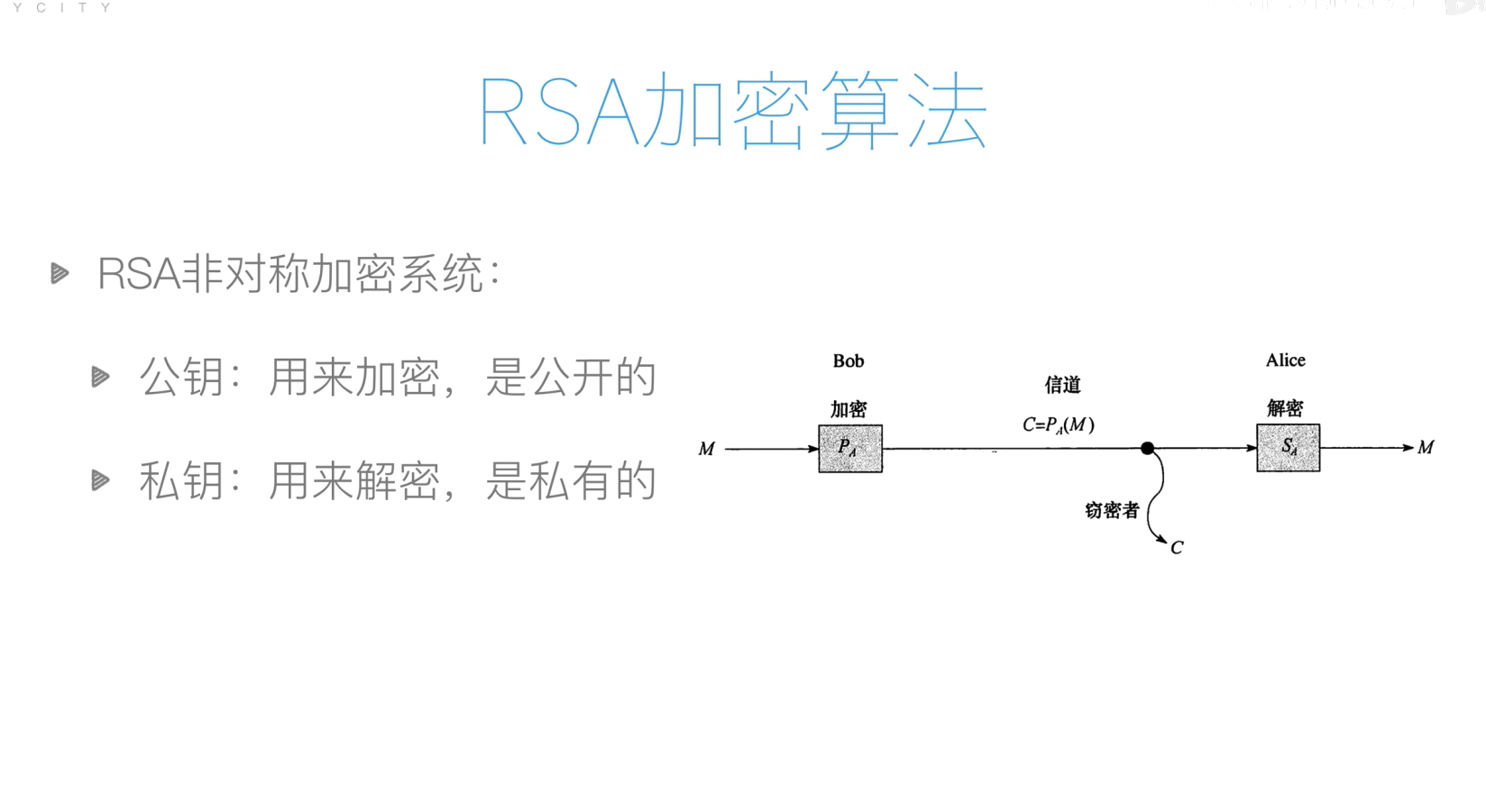


面向对象


设计模式




创建型模式
简单工厂模式


工厂方法模式


抽象工厂模式



建造者模式


单例模式


小结

结构型模式
适配器模式


桥模式



组合模式


外观模式


代理模式


行为型模式
责任链模式


观察者模式


模板方法模式


策略模式



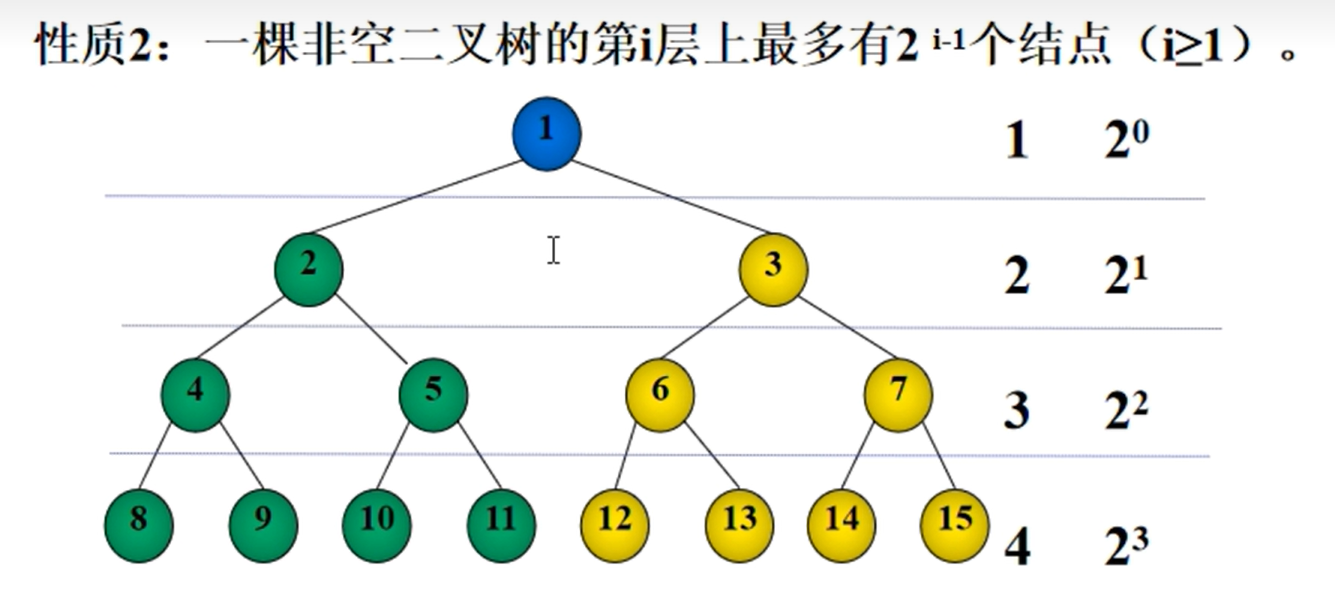 算法学习心得,源码均为Python实现
算法学习心得,源码均为Python实现

 浙公网安备 33010602011771号
浙公网安备 33010602011771号