虚树详解＋例子分析＋模板
概念：
给出一棵树.
每次询问选择一些点,求一些东西.这些东西的特点是,许多未选择的点可以通过某种方式剔除而不影响最终结果.
于是就有了建虚树这个技巧.....
我们可以用log级别的时间求出点对间的lca....
那么,对于每个询问我们根据原树的信息重新建树,这棵树中要尽量少地包含未选择节点. 这棵树就叫做虚树.
接下来所说的"树"均指虚树,原来那棵树叫做"原树".
构建过程如下:
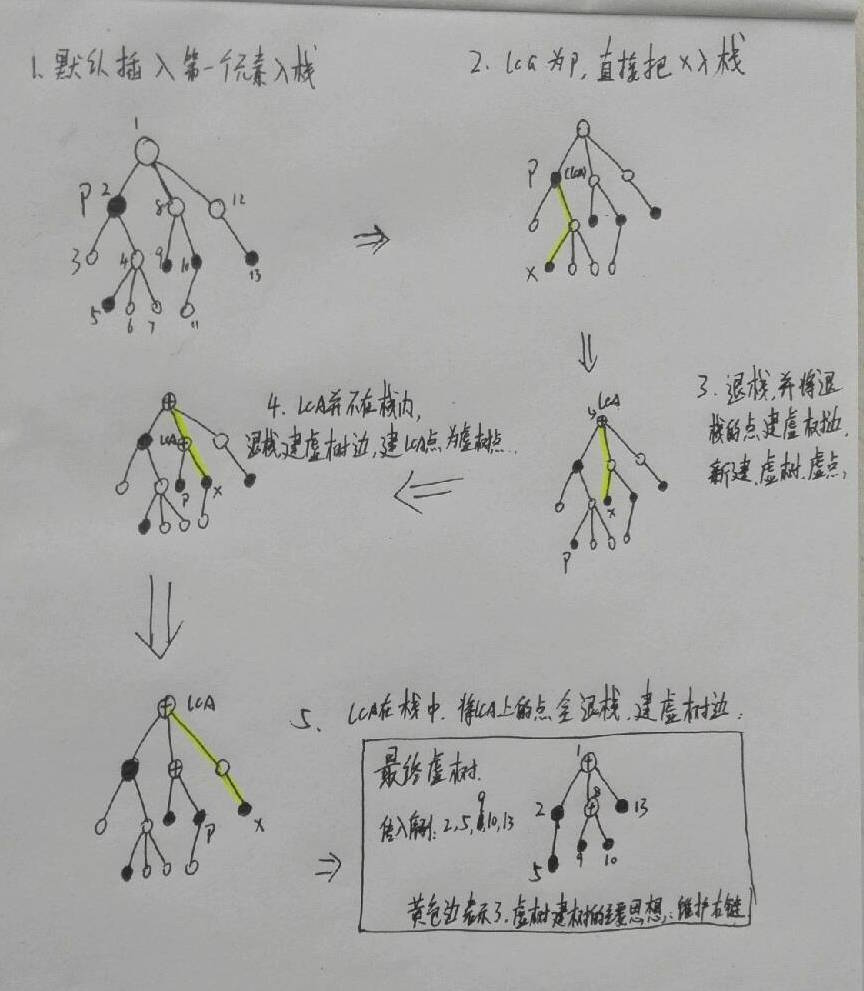
按照原树的dfs序号(记为dfn)递增顺序遍历选择的节点. 每次遍历节点都把这个节点插到树上.
首先虚树一定要有一个根. 随便扯一个不会成为询问点的点作根.（并不觉得是这样）
维护一个栈,它表示在我们已经(用之前的那些点)构建完毕的虚树上,以最后一个插入的点为端点的DFS链.
设最后插入的点为p(就是栈顶的点),当前遍历到的点为x.我们想把x插入到我们已经构建的树上去.
求出lca(p,x),记为lca.有两种情况:
1.p和x分立在lca的两棵子树下.
2.lca是p.
(为什么lca不能是x?
因为如果lca是x,说明dfn(lca)=dfn(x)<dfn(a),而我们是按照dfs序号遍历的,于是dfn(a)<dfn(x),矛盾.)
对于第二种情况,直接在栈中插入节点x即可,不要连接任何边(后面会说为什么).
对于第一种情况,要仔细分析.
我们是按照dfs序号遍历的(因为很重要所以多说几遍......),有dfn(x)>dfn(p)>dfn(lca).
这说明什么呢? 说明一件很重要的事:我们已经把lca所引领的子树中,p所在的子树全部遍历完了!
简略的证明:如果没有遍历完,那么肯定有一个未加入的点h,满足dfn(h)<dfn(x),
我们按照dfs序号递增顺序遍历的话,应该把h加进来了才能考虑x.
这样,我们就直接构建lca引领的,p所在的那个子树. 我们在退栈的时候构建子树.
p所在的子树如果还有其它部分,它一定在之前就构建好了(所有退栈的点都已经被正确地连入树中了),就剩那条链.
如何正确地把p到lca那部分连进去呢?
设栈顶的节点为p,栈顶第二个节点为q.
重复以下操作:
如果dfn(q)>dfn(lca),可以直接连边q->p,然后退一次栈.
如果dfn(q)=dfn(lca),说明q=lca,直接连边lca->p,此时子树已经构建完毕.
如果dfn(q)<dfn(lca),说明lca被p与q夹在中间,此时连边lca->q,退一次栈,再把lca压入栈.此时子树构建完毕.
如果不理解这样操作的缘由可以画画图.....
最后,为了维护dfs链,要把x压入栈. 整个过程就是这样.....
下图是自己画的一个例子：
附上模板:
///////////--虚树模板--/////////////////// //传入树的一个子集，若以按dfs序排好直接调用build_vtree //否则调用vsort //复杂度O( nlog(n) ) n是虚树的大小 #define N 11000 #define LN 20 ////////////--标准建邻接表--///////////// struct node { int to,next; }edge[2*N]; int cnt,pre[N]; void add_edge(int u,int v) { edge[cnt].to = v; edge[cnt].next = pre[u]; pre[u] = cnt++; } ////////////////////////////////////// int deep[N];//记录每个点的深度 int order[N];//记录每个点的访问次序 int indx=0; struct Lca_Online { int _n; int dp[N][LN]; void _dfs(int s,int fa,int dd) { deep[s] = dd; order[s] = ++indx; for(int p=pre[s];p!=-1;p=edge[p].next) { int v = edge[p].to; if(v == fa) continue; _dfs(v,s,dd+1); dp[v][0] = s; } } void _init() { for(int j=1;(1<<j)<=_n;j++) { for(int i=1;i<=_n;i++) { if(dp[i][j-1]!=-1) dp[i][j] = dp[ dp[i][j-1] ][j-1]; } } } void lca_init(int n) { _n = n; memset(dp,-1,sizeof(dp)); //_dfs(firstid,-1,0); indx = 0; _dfs(1,-1,0); _init(); } int lca_query(int a,int b) { if(deep[a]>deep[b]) swap(a,b); //调整b到a的同一高度 for(int i=LN-1;deep[b]>deep[a];i--) if(deep[b]-(1<<i) >= deep[a]) b = dp[b][i]; if(a == b) return a; for(int i=LN-1;i>=0;i--) { if(dp[a][i]!=dp[b][i]) a = dp[a][i],b = dp[b][i]; } return dp[a][0]; } }lca; int stk[N],top; int mark[N];//标示虚树上的点是否是无用点 vector<int>tree[N];//存边 vector<int>treew[N];//存权 void tree_add(int u,int v,int w) { tree[u].push_back(v); tree[v].push_back(u); treew[u].push_back(w); treew[v].push_back(w); } //使用前调用 lca.lca_init(n); 初始化 //返回虚树根节点,虚树的边默认为原树上两点的距离 int build_vtree(int vp[],int vn)//传入按dfs序数组，以及长度(要自己写按dfs排序的数组) { if(vn == 0) return -1; top = 0; stk[top++] = vp[0]; tree[ vp[0] ].clear(); treew[ vp[0] ].clear(); mark[ vp[0] ]=1; for(int i=1;i<vn;i++) { int v = vp[i]; int plca = lca.lca_query(stk[top-1], v);//最近公共祖先 if(plca == stk[top-1]) ;//不处理 else { int pos=top-1; while(pos>=0 && deep[ stk[pos] ]>deep[plca]) pos--; pos++; for(int j=pos;j<top-1;j++) { tree_add(stk[j],stk[j+1],deep[stk[j+1]]-deep[stk[j]]); } int prepos = stk[pos]; if(pos == 0) { tree[plca].clear(),treew[plca].clear(),stk[0]=plca,top=1; mark[plca] = 0; } else if(stk[pos-1] != plca) { tree[plca].clear(),treew[plca].clear(),stk[pos]=plca,top=pos+1; mark[plca] = 0; } else top = pos; tree_add(prepos,plca,deep[prepos]-deep[plca]); } tree[v].clear(); treew[v].clear(); stk[top++] = v; mark[v] = 1; } for(int i=0;i<top-1;i++) { tree_add(stk[i], stk[i+1], deep[stk[i+1]]-deep[stk[i]]); } return vp[0]; } //////////////--先排序，再建虚树--////////////////////// struct vnode { int order,id; }vg[N]; int vcmp(vnode t1,vnode t2) { return t1.order<t2.order; } int vsort(int vp[],int vn)//传入未排序的数组，以及长度. { for(int i=0;i<vn;i++) vg[i].id = vp[i],vg[i].order = order[ vp[i] ]; sort(vg,vg+vn,vcmp); for(int i=0;i<vn;i++) vp[i]=vg[i].id; return build_vtree(vp, vn); } //////////////////////////////////// //void dfs(int s,int fa) //{ // printf("%d ",s); // for(int i=0;i<tree[s].size();i++) // { // int v = tree[s][i]; // if(v == fa) continue; // dfs(v,s); // } //} // //int main() //{ // int n; // cin>>n; // cnt = 0; // memset(pre,-1,sizeof(pre)); // for(int i=1;i<n;i++) // { // int a,b; // cin>>a>>b; // add_edge(a, b); // add_edge(b, a); // } // int m; // cin>>m; // int save[100]; // for(int i=0;i<m;i++) scanf("%d",save+i); // lca.lca_init(n); // int root = vsort(save, m); // if(root != -1) // { // dfs(root,-1); // } // return 0; //} /* 7 1 3 1 2 2 6 3 5 3 4 4 7 3 6 7 5 */
