OO面向对象编程:第三单元总结
1.梳理JML语言的理论基础、应用工具链情况
(1)理论基础
JML是用于对Java程序进行规格化设计的一种表示语言,是一种行为接口规格语言(Behavior Interface Specification Language,BISL),基于Larch方法构建。BISL提供了对方法和类型的规格定义手段。所谓接口即一个方法或类型外部可见的内容。JML主要由Leavens教授在Larch上的工作,并融入了BetrandMeyer, John Guttag等人关于Design by Contract的研究成果。近年来,JML持续受到关注,为严格的程序设计提供了一套行之有效的方法。通过JML及其支持工具,不仅可以基于规格自动构造测试用例,并整合了SMT Solver等工具以静态方式来检查代码实现对规格的满足情况。一般而言,JML有两种主要的用法:
1) 开展规格化设计。这样交给代码实现人员的将不是可能带有内在模糊性的自然语言描述,而是逻辑严格的规格。
2) 针对已有的代码实现,书写其对应的规格,从而提高代码的可维护性。这在遗留代码的维护方面具有特别重要的意义。
通常情况下设计者在写代码时会在设计类代码结构时比较充分地使用面向对象的思想而淡化面向过程,但是在实现具体类和方法时,通常会恢复到面向过程的编程方式,但是如果有一种像类结构设计一样的能够高屋建瓴的忽略具体实现方式,但是能够较为明晰的体现该类或方法的输入与输出以及过程中应当时钟保持的约束的语言就会改善这种情况。这也就是为什么JML会存在。
语法相对完备:
-
JML表达式
-
原子表达式
-
量化表达式
-
集合表达式
-
操作符
-
-
方法规格
-
Pre-condition
-
Post-condition
-
Side-effects
-
-
类型规格
(2)工具链情况
OpenJML
自动check JML规格文档并生成报告。
Junit自动测试类
2.部署JMLUnitNG/JMLUnit,针对Graph接口的实现自动生成测试用例, 并结合规格对生成的测试用例和数据进行简要分析
(选择相关的简单方法,自己补充规格,确保未使用\exists或\forall表达式,使用jmlunit或jmlunitng来生成测试数据,并分析所生成数据的特点。注意自己补充规格时,应尽可能保证规格反应相应方法的设计。如仍然存在困难可以考虑退而求其次,做力所能及的即可(比如仅针对PathContainer的部分方法))
(1)安装OpenJML
-
OpenJML 可以在 OpenJML 官方 github 仓库的 Releases 界面处获取
-
解压后将.jar文件和Solover-Windows(在Windows系统下)放在同一文件夹内(我放在F:\jmlunitng文件夹下)
-
在该文件夹下使用命令:
$ java -jar openjml.jar "$@"完成安装$ java -jar openjml.jar "$@"
JML options:
-dir Process all files, recursively, within this directory
-dirs Process all files, recursively, within these directories (listed as separate arguments, up to an argument that begins with a - sign)
-- Terminates option processing - all remaining arguments are files
-keys Identifiers for optional JML comments
-command The command to execute (check,esc,rac,compile)
-check Does a JML syntax check [-command=check]
-compile Does a Java-only compile [-command=compile]
-rac Enables generating code instrumented with runtime assertion checks [-command=rac]
-esc Enables static checking [-command=esc]
-boogie Enables static checking with boogie
-java When on, the tool uses only the underlying javac or javadoc compiler (must be the first option)
...
...
...
-infer-persist-path Specify output directory of specifications (overrides -specspath)
-infer-max-depth The largest CFG we will agree to process
-infer-timeout Give up inference after this many seconds. A value of -1 will wait indefinitely
-infer-dev-mode Special features for developers.
-infer-analysis-types Enables specific analysis types. Takes a comma seperated list of analysis types. Support kinds are: REDUNDANT, UNSAT, TAUTOLOGIES, FRAMES, PURITY, and VISIBILITY
(2)安装JMLUnitTNG
直接从官网获取 jar 包,安装方法同上一篇文章。
官网链接:http://insttech.secretninjaformalmethods.org/software/jmlunitng/
jar 包链接:http://insttech.secretninjaformalmethods.org/software/jmlunitng/assets/jmlunitng.jar
调用命令$ java -jar jmlunitng.jar "$@"完成安装
$ java -jar jmlunitng.jar "$@"
JMLUnitNG - Generate TestNG Classes for JML-Annotated Java
java -jar jmlunitng.jar [OPTION] ... path-list
Generates unit tests for all Java source files listed in,
or recursively contained in directories listed in, path-list.
-d, --dest [DIRECTORY] : Use DIRECTORY as the output directory for
generated classes.
...
...
...
--prune : Remove from the destination path any old JMLUnitNG-
generated files for path-list that do not conform to the current
API of the classes under test and the current JMLUnitNG options.
If no destination path is set, all files and directories in
path-list are pruned.
--no-gen : Do not generate tests, use in conjunction with --clean
or --prune to remove unwanted JMLUnitNG-generated files.
--dry-run : Display status/progress information about the operations
that would be performed but do not modify the filesystem.
-v, --verbose : Display status/progress information.
-h, --help : Display this message.
Version: 1.4 (116/OpenJML-20131218-REV3178)
(3)创建源文件
(根据老师和同学的反馈,openjml可能还不支持对\exists和\forall表达式的分析和验证问题,故以下规格中均尽量减少\exists和\forall。)
以getNode和size()为例:
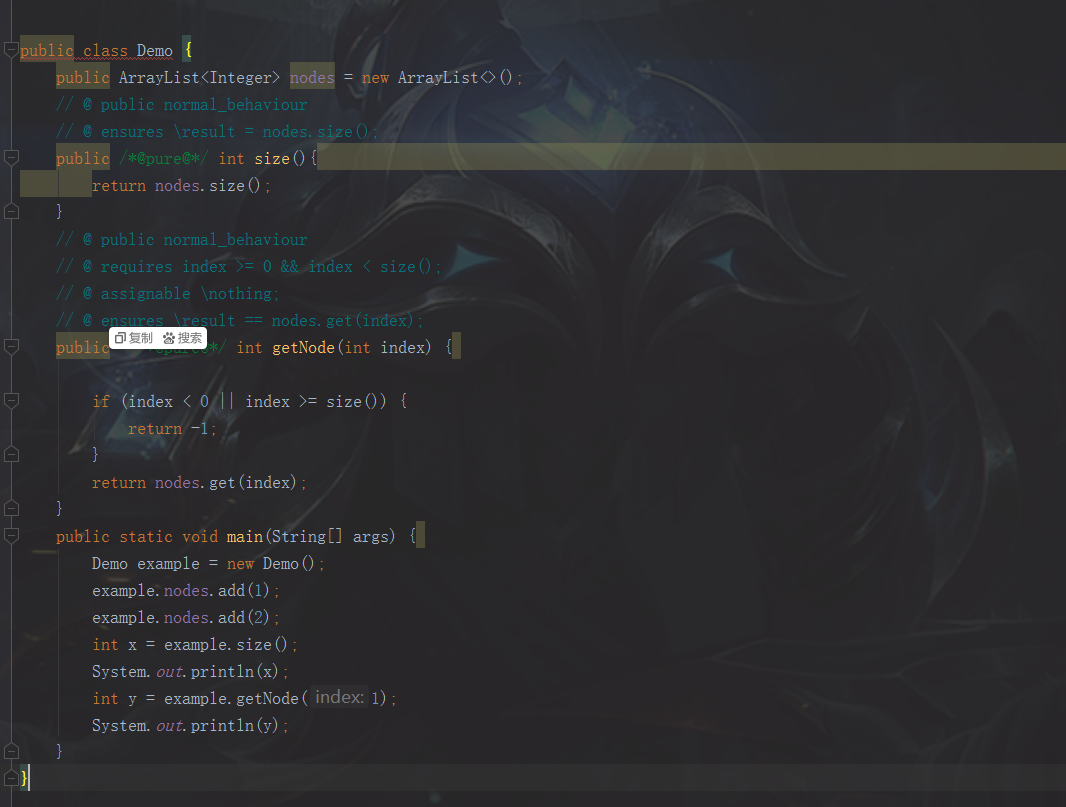
(4)生成测试文件

demo
├── Demo_InstanceStrategy.java
├── Demo.java
├── Demo_JML_Data
│ ├── ClassStrategy_int.java
│ ├── ClassStrategy_java_lang_String1DArray.java
│ ├── ClassStrategy_java_lang_String.java
│ ├── compare__int_lhs__int_rhs__0__lhs.java
│ ├── compare__int_lhs__int_rhs__0__rhs.java
│ └── main__String1DArray_args__10__args.java
├── Demo_JML_Test.java
├── PackageStrategy_int.java
├── PackageStrategy_java_lang_String1DArray.java
└── PackageStrategy_java_lang_String.java
(5)编译运行
用 javac 编译 JMLUnitNG 的生成文件
执行命令$ javac -cp jmlunitng.jar demo/**/**.java
用 jmlc 编译自己的文件,生成带有运行时检查的 class 文件
执行命令$ java -jar openjml.jar -rac demo/Demo.java
执行命令$ javac -cp jmlunitng.jar demo/**.java
执行 java -cp jmlunitng-1_4.jar demo.Demo_JML_Test
运行结果
Test[TestNG] Running:
Command line suite
Passed:racEnabled()
Passed: constructor DemoO
Passed: <<demo.Demo@2eafffde>>.getNode(-2147483648)
Passed: <<demo.Demo@59690aa4>>.getNode(0)
Passed: <<demo.Demo@6842775d>>.getNode(2147483647)
Passed: <<demo.Demo@1761e840>>.size()
2
2
Passed: static main(nu1l)
2
2
Passed: static main({})
===================================================================================================
Command ine suite
Total tests run: 8, Failures: 1, Skips: 0
===================================================================================================
3.按照作业梳理自己的架构设计,并特别分析迭代中对架构的重构
(1)第1次规格作业
public class MyPath implements Path {
private ArrayList nodes = new ArrayList();
public MyPath(int[] nodeList) {
int i;
for (i = 0; i < nodeList.length; i++) {
nodes.add(nodeList[i]);
}
}
}
在Path类中,我用了动态数组储存一条路径中的各个节点
public class MyPathContainer implements PathContainer {
private ArrayList<Path> plist = new ArrayList<Path>();
private ArrayList pidList = new ArrayList();
}
在PathContainer类中,我使用了两个arraylist来分别存储path的id和path本身。
因为没有使用Hashmap的缘故,在
public int getDistinctNodeCount() {
int i;
int j;
HashSet set = new HashSet();
for (i = 0; i < plist.size(); i++) {
Path p = plist.get(i);
for (j = 0; j < p.size(); j++) {
set.add(p.getNode(j));
}
}
return set.size();
}
中,会达到O(n^3)的时间复杂度,在测试数据较大时,会出现超时的bug现象。
(2)第2次规格作业
Path类以及其中的相关方法相比上次作业并无较大的变化。
在Graph类中:
public class MyGraph implements Graph {
private ArrayList<Path> plist = new ArrayList<Path>();
private ArrayList pidList = new ArrayList();
private ArrayList haha = new ArrayList(); //len=252
private int[][] graph = new int[252][252];
private int[][] dist = new int[252][252];
private int tempid = 1;
private int distinctcount = 0;
private boolean change = false;
private boolean changec = false;
}
其中plist和pidlist仍然与上次作业使用相同的数据结构
haha数组是我的映射方式的体现,虽然每个节点中的标识可以是int范围内的任意整数,但是题目有要求:任何时候总的互异节点个数不超过250个,所以我的数组长度lenth也是250
两个二维数组是为了使用Floyd最短路径算法来计算最短距离而设立的两个250*250的静态数组
我的Floyd算法也是对应的邻接矩阵来写的:
import java.util.ArrayList;
public class Floyd {
/*
* floyd最短路径。
* 即,统计图中各个顶点间的最短路径。
* 参数说明:
* dist -- 长度数组。即,dist[i][j]=sum表示,"顶点i"到"顶点j"的最短路径的长度是sum。
*/
public static void floyd(int[][] dist, ArrayList mvexs,
int[][] mmatrix, int inf) {
// 初始化
for (int i = 0; i < mvexs.size(); i++) {
for (int j = 0; j < mvexs.size(); j++) {
dist[i][j] = mmatrix[i][j]; // "顶点i"到"顶点j"的路径长度为"i到j的权值"。
}
}
// 计算最短路径
for (int k = 0; k < mvexs.size(); k++) {
for (int i = 0; i < mvexs.size(); i++) {
for (int j = 0; j < mvexs.size(); j++) {
// 如果经过下标为k顶点路径比原两点间路径更短,则更新dist[i][j]和path[i][j]
int tmp;
if (dist[i][k] == inf || dist[k][j] == inf) {
tmp = inf;
} else {
tmp = dist[i][k] + dist[k][j];
}
if (dist[i][j] > tmp) {
// "i到j最短路径"对应的值设,为更小的一个(即经过k)
dist[i][j] = tmp;
}
}
}
}
}
}
应用相关算法后,两点之间的最短路径结果就存储在dist数组中了。
(3)第3次规格作业
Path类以及其中的相关方法相比上次作业并无较大的变化。
在RailwaySystem类中:
public class MyRailwaySystem implements RailwaySystem {
private ArrayList<Path> plist = new ArrayList<Path>();
private ArrayList pidList = new ArrayList();
private ArrayList haha = new ArrayList(); //len=150
private int[][] graph = new int[150][150];
private int[][] dist = new int[150][150];
private int[][] temp1 = new int[150][150];
private int[][] temp2 = new int[150][150];
private int[][] temp3 = new int[150][150];
private int tempid = 1;
private int distinctcount = 0;
private boolean change = false;
private boolean changec = false;
private boolean changeprice = false;
private boolean changecount = false;
private boolean changevalue = false;
}
新增了三个二维数组:
private int[][] temp1 = new int[150][150];
private int[][] temp2 = new int[150][150];
private int[][] temp3 = new int[150][150];
主要是对应三个主要需解决的问题:
最小换乘次数、最少票价、最少不满意度
受到了讨论区中相关大佬的启发:
四个题都是完全一样的,区别是
-
初始化的方式(拆点/不拆点)
-
初始化权重的定义(1/路径长度/满意度)
-
每加上一条边(加/不加)换乘常数
然后用一个算法(比如dij)就能够全部搞定。拆点是指把以前的一条路径涉及到的点变为完全无向图,完全无向图的每一条边当成独立的path考虑。
所以只需要在原来矩阵的基础上,按照三种特定的赋值方式生成3个特定的矩阵,用来解决不同的问题。
在Fill方法中便是对三个temp矩阵的赋权值过程:
public static void fillforprice(ArrayList<Path> plist,int[][] temp, ArrayList haha) {
...
}
public static void fillforcount(ArrayList<Path> plist,int[][] temp, ArrayList haha) {
...
}
public static void fillforvalue(ArrayList<Path> plist,int[][] temp, ArrayList haha) {
...
}
我的Dijkstra算法也是对应的邻接矩阵来写的:
/*
* Dijkstra最短路径。
* 即,统计图中"顶点vs"到其它各个顶点的最短路径。
*
* 参数说明:
* vs -- 起始顶点(start vertex)。即计算"顶点vs"到其它顶点的最短路径。
* prev -- 前驱顶点数组。即,prev[i]的值是"顶点vs"到"顶点i"的最短路径所经历的全部顶点中,位于"顶点i"之前的那个顶点。
* dist -- 长度数组。即,dist[i]是"顶点vs"到"顶点i"的最短路径的长度。
*/
public static int dijkstra(int vs, int e,
int inf, ArrayList mvexs, int[][] mmatrix) {
int[] prev = new int[150];
int[] dist = new int[150];
// flag[i]=true表示"顶点vs"到"顶点i"的最短路径已成功获取
boolean[] flag = new boolean[mvexs.size()];
// 初始化
for (int i = 0; i < mvexs.size(); i++) {
flag[i] = false; // 顶点i的最短路径还没获取到。
prev[i] = 0; // 顶点i的前驱顶点为0。
dist[i] = mmatrix[vs][i]; // 顶点i的最短路径为"顶点vs"到"顶点i"的权。
}
// 对"顶点vs"自身进行初始化
flag[vs] = true;
dist[vs] = 0;
// 遍历mVexs.length-1次;每次找出一个顶点的最短路径。
int k = 0;
for (int i = 1; i < mvexs.size(); i++) {
// 寻找当前最小的路径;
// 即,在未获取最短路径的顶点中,找到离vs最近的顶点(k)。
int min = inf;
for (int j = 0; j < mvexs.size(); j++) {
if (flag[j] == false && dist[j] < min) {
min = dist[j];
k = j;
}
}
// 标记"顶点k"为已经获取到最短路径
flag[k] = true;
// 修正当前最短路径和前驱顶点
// 即,当已经"顶点k的最短路径"之后,更新"未获取最短路径的顶点的最短路径和前驱顶点"。
for (int j = 0; j < mvexs.size(); j++) {
int tmp;
if (mmatrix[k][j] == inf) {
tmp = inf;
} else {
tmp = (min + mmatrix[k][j]);
}
if (flag[j] == false && (tmp < dist[j])) {
