工作分配问题

一、题目：工作分配问题

二、问题描述

设有n件工作分配给n个人。将工作i分配给第j个人所需的费用为cij 。 设计一个算法，对于给定的工作费用，为每一个人都分配1 件不同的工作，并使总费用达到最小。

在这里给出一组输入。例如：

3
10 2 3
2 3 4
3 4 5

在这里给出相应的输出。例如：

9

三、算法描述：

解空间：空间树为n棵多叉树，比如有n人对n建工作，那么就会有 n课树 每个子节点有n个叉口，这么多的叉口得靠一个记录数组b来进行约束剪去。该树的根结点是第一个人选某一件工作（即第一棵树的根结点是第一件工作，第二课树的根结点是选择了第二件工作.......第n课的根结点是第一个人选择了第n个工作），依次类推下去第二层就是第二个人选择某件工作，在此约束函数if（！b[i]）就可以用来判断该工作是否已经被选择，比如第一棵树第一个人已经选择第一件工作并且作为了根结点了，那么第二人就不能再选择第一件工作了，那么第二层第一件工作的那个叉口接下去的所有节点构成的树枝也就会被约束函数剪除掉。  在构建数的时候在脑子中想固然是要将整课树构建出来，才有利于我们的遍历，然后我们只需要在遍历的时候使用一些限制的函数去吧树枝剪除掉就行了，就不会出现很大的遍历次数。

所以在代码中我们进行了n循环的遍历，其实就是相当于对n课树的遍历，不断找出最优值，在此运用限界函数sum<minn 即当遍历到该点的时候，如果该点当前的sum值大于当前最优值minn的话就不再进行遍历，以为再遍历下去的话那个树枝产生的解也不可能比当前最优解小，那就没有意义，所以也就可以将该树枝剪除了，也就是将该点视为死结点，然后回溯上去。找到这棵树的最优值之后，进入第二个循环遍历第二棵空间树（也就是第一个人选择了第二件工作的那棵树），不断遍历找到最优值然后赋值给minn。

 

 

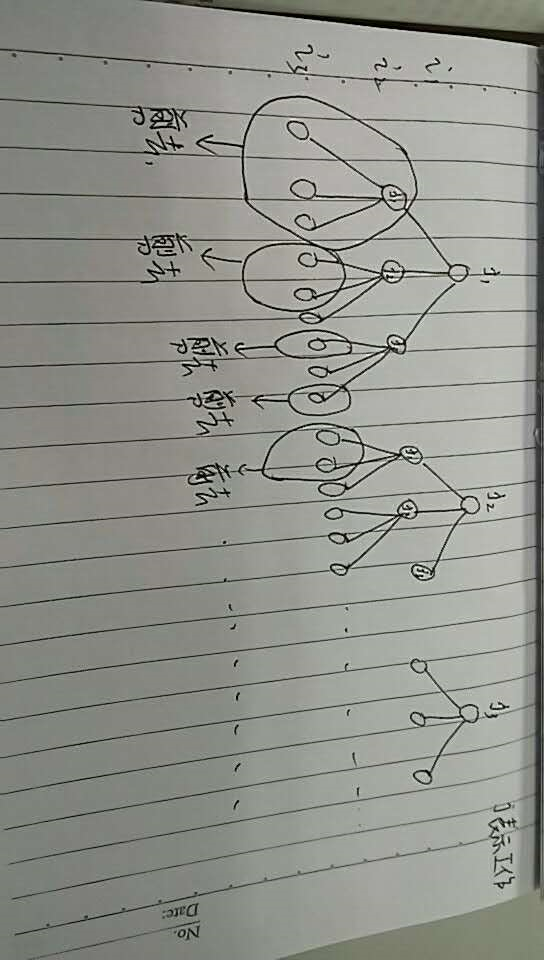
剪枝函数：   sum<minn 为限界函数，当到达该节点时，如果所需耗费的总费用sum小于当　前最优解费用minn时就继续深度优先遍历这个节点以下的部分，否则剪枝。!b[r]为约束函数，当该节点已经在问题的解中的时候就不再访问它。

 

源代码：

#include<iostream>
using namespace std;
int a[100][100],sum=0,minn=2147483647,i,j,n;
int b[100];
void dfs(int dep)
{
    int r;
    for (r=1;r<=n;++r)//dep表示第几个人，r表示工作
      if (!b[r])
      {
          b[r]=1;
          sum+=a[dep][r];//a[dep][r]表示第dep个人做第r个工作的费用
          if (dep==n&&sum<minn)
          {
                 minn=sum;
          }
          if(dep!=n)
           {
               if (sum<minn)//剪枝
                  dfs(dep+1);
         }
          sum-=a[dep][r];//回溯一步
          b[r]=0;
      }
}
int main()
{
    cin>>n;
    for (i=1;i<=n;++i)
      for (j=1;j<=n;++j)
        cin>>a[i][j];
    dfs(1);
    cout<<minn<<endl;
    return 0;
}

 四、心得体会

 在算法的酝酿过程中，最好是把空间树直接画出来，会比较清晰一些，分析问题能够更加简便。而且不要直接把画出来的空间树就直接用函数剪枝，吧完整的树画出来，然后分析一下样例是怎么走的流程，那样子将会更加有利于你解题。