仿射集、凸集和锥的概念

1、仿射集和凸集

1.1 仿射集相关概念

仿射（affine）定义：对于集合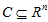 ，如果通过集合C中任意两个不同点之间的直线仍在集合C中，则称集合C为仿射（affine）。

也就是说，C包括了在C中任意两点的线性组合，即：

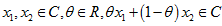
这个概念可以推广到n个点，即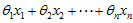 ，其中 。也称为仿射组合。

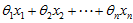仿射集（affine set）定义：仿射集包含了集合内点的所有仿射组合。若C是仿射集， ，，则点也属于C.

仿射包（affine hull）的定义：仿射包是包含C的最小的仿射集，表示为：

 

1.2 凸集的相关概念

凸（convex）的定义：对于集合 ，如果通过集合C中任意两个不同点之间的线段仍在集合C中，则称集合C为凸（convex）。

注：所有仿射集都是凸的，因为它包含集合中任意不同点的所有直线

凸组合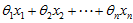：的点，其中和 ，则称点 的凸组合。

凸组合与仿射组合的区别：在凸组合中，参数 必须大于等于0。

凸集（convex set）：该集合包含了所有点的凸组合。

凸包（convex hull）：最小的凸集，表示为：

注：1）凸包总是凸的

2）若B是凸集并且包含C，则

在二维欧几里得空间中，凸包可想象为一条刚好包着所有点的橡皮圈

 

1.3、锥

锥（cone）的定义：若对于任意 和 ，有 ，则称为锥。如果集合C既是凸也是锥，则称为凸锥。

锥组合：的点，其中，则称为锥组合。也称为非负线性组合。

若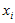在凸锥C中，则的所有凸组合在C中；相反，集合C为凸锥，当且仅当它包含了所有元素的凸组合。

 

锥包（cone hull）：集合C中所有锥组合的集合，也是包含C的最小凸锥。即

 

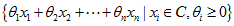
2、例子

空集、点、整个空间都是仿射（affine），因此也是凸（convex）

任意线是仿射（affine），若过原点，则为凸锥（convex cone）

线段是凸（convex），但不是仿射

形式如 的射线是凸，但不是仿射

任意子空间是仿射和凸锥

 

超平面是仿射集（affine set）

半平面是凸集（convex set）

球体和椭圆体是凸集

Norm ball 和norm cone是凸锥

多面体（polyhedra）是凸集

 

 

 

参考文献：convex optimization[Stephen Boyd]