二分图学习笔记

首先，看看二分图的定义

我看不懂的度娘解释

接下来阐释我自己初学的理解

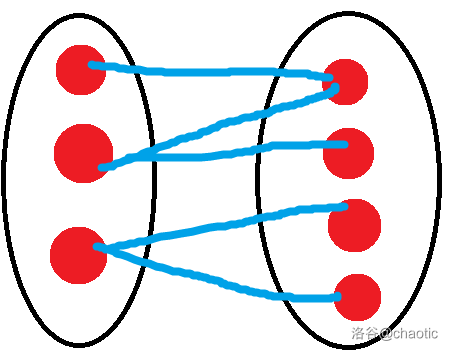
就是有两个集合中分别有好多点，同一个集合中的点两两之间没有连线，但是集合之间可以有连线

接下来讨论一下判定二分图

我自己有一个麻烦独特的bfs方法，它的本质与dfs相同

先将任意一个未染色的点染成任意一个颜色，这里染成1，然后将这个点压入队列

然后进入一个while循环，取出一个点，因为已染色，知道与它有连线的点都应该异色，那么就将这些点染色。

如果已经有颜色了，颜色已经相异，那么没事，找下一个点，如果同色，那就出大问题了，矛盾，不是二分图。

如果没有颜色，那么就染一个不同的颜色（3-color[x]），并将这一个点压入队列

bfs代码：

int check()
{
	int cnt=0;//记录已经染了多少个点
	while(cnt<n)
	{
		for(int i=1;i<=n;i++)//要二分所有点
		{
			if(flag[i]==0)
			{
				q.push(i);
				flag[i]=1;
				break;
			}
		}
		while(q.size())
		{
			cnt++;//染色点数加一
			int x=q.front();
			q.pop();
			for(int i=0;i<e[x].size();i++)
			//这里e数组储存边
			//我采用了动态数组
			//e[x].size()可以理解成e数组大小
			//之后就当成普通数组
			{
				int y=e[x][i];//取出数组的值
				if(flag[x]==flag[y]) return 1;//同色判错
				if(flag[y]==0)//异色染色
				{
					flag[y]=3-flag[x];
					q.push(y);
				}
			}
		}
	}
	return 0;
}

接下来，也要稍微解释一下正解dfs

先讲主要dfs部分

先是一个未染色点，同样将其染色，然后循环枚举每一条边，对应的点要先判有无色，同色，返回false，异色，继续循环，无色，从这一点再次dfs，返回结果若false则返回false

dfs主要部分：

bool dfs(int x,int c)//c表x要染的颜色
{
	color[x]=c;
	for(int i=0;i<e[x].size();i++)//枚举访问每条边
	{
		int y=e[x][i];
		if(color[y]==c) return 0;//同色则false
		if(color[y]==0&&!dfs(y,-c)) return 0;//下一点false则当前点也false
	}
	return 1;
}

同样，要二分所有点，所以要再配一个循环

dfs次要部分：

bool check()
{
	for(int i=1;i<=n;i++)
		if(!color[i])//判是否染过
			if(!dfs(i,1)) return 0;
}

接下来要开始有趣的匈牙利算法

为了不冒犯他人，此处以男1,2,3,4，女1,2,3,4代替

初始时（黑表可能关系，红表确认关系，紫表将断裂关系）

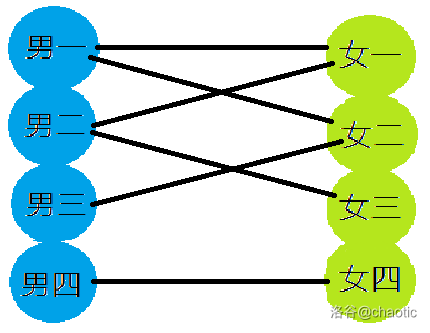
然后男1开始找npy，从上至下，找到女一，相连

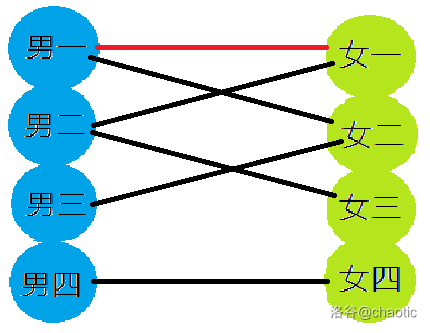
然后男二也要女一，男一让位，男二与女一连线

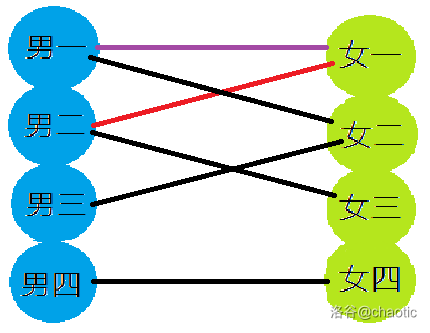
男一再找下一个，于是找到女二，连线

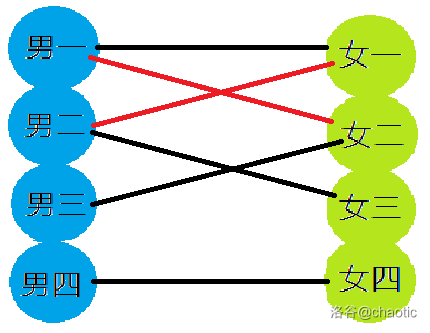
男三开始找，要女二，男一将让位

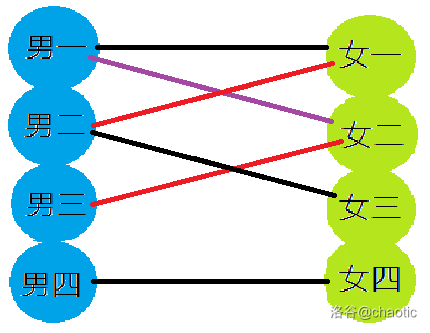
然鹅，男一没有备胎了，让位后就单着了

于是不让

男三开始找下一个

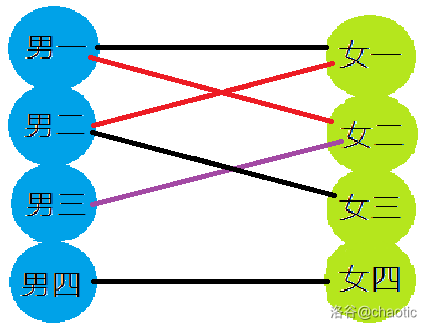
男三没备胎了，单着

男四欲与女四连线，女四还单着，直接连线

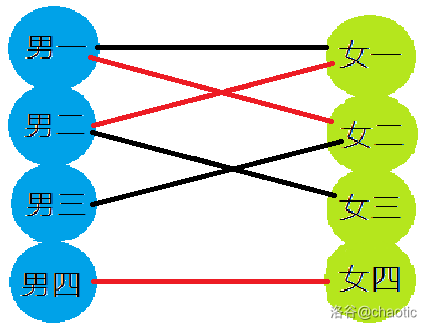
于是答案就是3

从上述过程中，我们可以抓住匈牙利算法的几个要点：

1、从上至下找

2、若前者能退（也可以再把第三对情侣拆掉），后来者先得

3、若前者不能退，后来者找下一个

4、无所得，单着，ans不加，否则ans++