Codeforces 671 A——Recycling Bottles——————【思维题】

 Recycling Bottles

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

It was recycling day in Kekoland. To celebrate it Adil and Bera went to Central Perk where they can take bottles from the ground and put them into a recycling bin.

We can think Central Perk as coordinate plane. There are n bottles on the ground, the i-th bottle is located at position (xi, yi). Both Adil and Bera can carry only one bottle at once each.

For both Adil and Bera the process looks as follows:

1. Choose to stop or to continue to collect bottles.
2. If the choice was to continue then choose some bottle and walk towards it.
3. Pick this bottle and walk to the recycling bin.
4. Go to step 1.

Adil and Bera may move independently. They are allowed to pick bottles simultaneously, all bottles may be picked by any of the two, it's allowed that one of them stays still while the other one continues to pick bottles.

They want to organize the process such that the total distance they walk (the sum of distance walked by Adil and distance walked by Bera) is minimum possible. Of course, at the end all bottles should lie in the recycling bin.

Input

First line of the input contains six integers ax, ay, bx, by, tx and ty (0 ≤ ax, ay, bx, by, tx, ty ≤ 109) — initial positions of Adil, Bera and recycling bin respectively.

The second line contains a single integer n (1 ≤ n ≤ 100 000) — the number of bottles on the ground.

Then follow n lines, each of them contains two integers xi and yi (0 ≤ xi, yi ≤ 109) — position of the i-th bottle.

It's guaranteed that positions of Adil, Bera, recycling bin and all bottles are distinct.

Output

Print one real number — the minimum possible total distance Adil and Bera need to walk in order to put all bottles into recycling bin. Your answer will be considered correct if its absolute or relative error does not exceed 10 - 6.

Namely: let's assume that your answer is a, and the answer of the jury is b. The checker program will consider your answer correct if .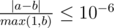

Examples

input

3 1 1 2 0 0
3
1 1
2 1
2 3

output

11.084259940083

input

5 0 4 2 2 0
5
5 2
3 0
5 5
3 5
3 3

output

33.121375178000

Note

Consider the first sample.

Adil will use the following path: .

Bera will use the following path: .

Adil's path will be 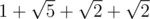 units long, while Bera's path will be  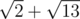units long.

 

题目大意： 给你ax,ay, bx,by, tx,ty。a、b两个人的坐标和垃圾桶的坐标。下面是n，然后n个瓶子的坐标x_i,y_i。两个人都只能拿到一个瓶子然后送回垃圾桶，然后再去捡其他瓶子。问你当所有瓶子都放入垃圾桶时，两个人一共走的最短距离是多少。

解题思路：假设a，b两人和垃圾桶在同一初始位置。那么所有瓶子放入垃圾桶时的距离为2*sigma(dist_i)，dist表示垃圾桶到其他瓶子的距离，我们把这个值设为sum。现在考虑a如果开始捡第一瓶子i，那么所要走的距离为disa[i]-dist[i]+sum，考虑b如果开始捡第一个瓶子j，那么要走的距离为disb[i]-dist[i]+sum。现在我们维护两个数组a[i]表示a第一次捡i这个瓶子时要走的距离，b[i]表示b第一次要捡i瓶子时要走的距离。我们维护b最小的两个值，同时记录id。然后枚举a数组，同时，如果所维护的两个id中有一个是所枚举的a数组下标，那么b就取另一个，否则取最小的值更新结果。

#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<math.h>
#include<string>
#include<iostream>
#include<queue>
#include<stack>
#include<map>
#include<vector>
#include<set>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
#define mid (L+R)/2
#define lson rt*2,L,mid
#define rson rt*2+1,mid+1,R
const int mod = 1e9+7;
const int maxn = 1e5+200;
const LL INF = 0x3f3f3f3f3f3f3f3f;
struct Coor{
    double x, y;
}coors[maxn];
double Distan(Coor a, Coor b){
    return sqrt((a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y));
}
double disa[maxn], disb[maxn];
int main(){
    int n;
    Coor a, b, t;
    while(scanf("%lf%lf %lf%lf %lf%lf",&a.x,&a.y,&b.x,&b.y,&t.x,&t.y)!=EOF){
        scanf("%d",&n);
        double dt;
        double sum = 0;
        double opt1 = double(INF), opt2 = double(INF);
        int opt1id = 1, opt2id = 1;
        for(int i = 1; i <= n; i++){
            scanf("%lf%lf",&coors[i].x,&coors[i].y);
            dt = Distan(coors[i], t);
            sum += 2.0*dt;
            disa[i] = Distan(coors[i], a) - dt;
            disb[i] = Distan(coors[i], b) - dt;
            if(disb[i] < opt1){
                swap(opt1, opt2);
                swap(opt1id,opt2id);
                opt1 = disb[i];
                opt1id = i;
            }else if(disb[i] < opt2){
                opt2 = disb[i];
                opt2id = i;
            }
        }
        double ans = double(INF);
        for(int i = 1; i <= n; i++){
            ans = min(ans, sum + disa[i]);
        }
        for(int i = 1; i <= n; i++){
            ans = min(ans, sum + disb[i]);
        }
        if(n == 1){
            printf("%.8lf",ans); continue;
        }
        for(int i = 1; i <= n; i++){
            if(i == opt1id){
                ans = min(ans, sum + disa[i]+disb[opt2id]);
            }else{
                ans = min(ans, sum + disa[i] + disb[opt1id]);
            }
        }
        printf("%.7lf",ans);
    }
    return 0;
}