AVL树

定义

一棵二叉树时高度平衡的。如果 T 是一棵非空二叉树，T_L和 T_R 分别是 T 的左子树和右子树，H_L和 H_R是 T_L 和 T_R 的高度。那么当T是高度平衡的当且仅当:

T_L和 T_R是高度平衡的。
Abs(H_L - H_R) <= 1

高度平衡的二叉树的定义要求其所有子树也是高度平衡的。由定义引入平衡因子（BalanceFactor），取值 -1、0、1代表着 H_L- H_R。

旋转

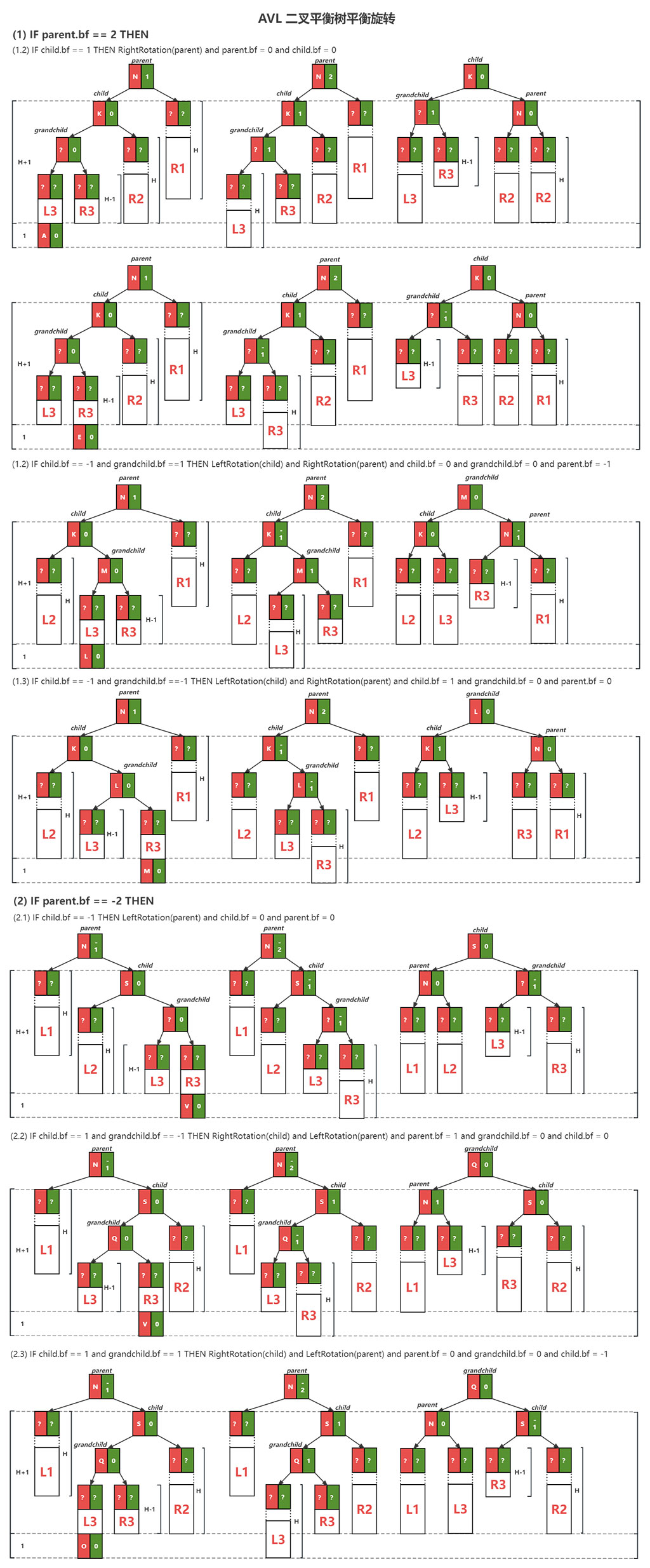
由插入和删除操作导致二叉树失去平衡，也就是平衡因子大于 1 或者小于 -1。通过当前结点 parent 和子节点 child 以及子孙结点 grandchild 的指向关系，有 LL、RR、LR、RR关系。如下图

平衡子树

左子树平衡

左子树高度减去右子树高度大于等于 2，左子树失去平衡，进行旋转后再次平衡，这里分为两种情况（令当前结点为 parent 左孩子为 child ）：

LL 型

左子树的左子树的高度增加
左子树的右子树高度减少

如果 child 的平衡因子为 1 则仅需进行右旋转即可，旋转后， parent 和 child 的平衡因子设置为 0，图中 (1.1) 所示。

LR 型

左子树的右子树的高度增加
左子树的左子树高度减少

如果 child 的平衡因子为 -1 ，则需要进行两次旋转，先对 child 进行左旋，然后对 parent 进行右旋，取 child 的右孩子 grandchild：

如果 grandchild 的平衡因子等于 1 则 child 的平衡因子设置为 0 ，parent 的平衡因子设置为 -1，grandchild 的平衡因子设置为0，图中（1.2）所示
如果 grandchild 的平衡因子等于 -1 则 child 的平衡因子设置为 1， parent 的平衡因子设置为 0， grandchild 的平衡因子设置为0，图中（1.3）所示。

 1     private void leftBalance(AvlNode<T> node) {
 2         AvlNode<T> child = node.getLeft();
 3         if (child.getBf() == LH) {
 4             /* 左子树 的 左子树增高 LL */
 5             right_Rotation(node);
 6             node.setBf(EH);
 7             child.setBf(EH);
 8         } else {
 9             /* 左子树 的 右子树增高 LR */
10             AvlNode<T> grandChild = child.getRight();
11             switch (grandChild.getBf()) {
12                 case RH: {
13                     node.setBf(EH);
14                     child.setBf(LH);
15                     break;
16                 }
17                 case EH : {
18                     node.setBf(EH);
19                     child.setBf(EH);
20                     break;
21                 }
22                 case LH : {
23                     node.setBf(RH);
24                     child.setBf(EH);
25                     break;
26                 }
27             }
28             grandChild.setBf(EH);
29 
30             left_Rotation(child);
31             right_Rotation(node);
32         }
33     }

右子树平衡

左子树高度减去右子树高度大于等于 -2，右子树失去平衡，进行旋转后再次平衡，这里分为两种情况（令当前结点为 parent 右孩子为 child ）：

RL 型

右子树的左子树高度增加
右子树的右子树高度减少

如果 child 的平衡因子为 1 则需要进行两次旋转，先对 child 进行右旋然后对 parent 进行左旋，取 child 的左孩子 grandchild ：

如果 grandchild 的平衡因子为 1 则旋转后设置 parent 的平衡因子为 0， child 的平衡因子为 -1， grandchild 平衡因子为0，图中（2.3）所示。
如果 grandchild 的平衡因子为 -1 则旋转后设置 parent 的平衡因子为 1，child 的平衡因子为 0， grandchild 平衡因子为0，图中（2.2）所示。

RR 型

右子树的右子树高度增加
右子树的左子树高度减少

如果 child 的平衡因子为 -1 则进行一次左旋即可，旋转后设置 parent 的平衡因子为 0，child 的平衡因子为 0，图中（2.1）所示。

 1     private void rightBalance(AvlNode<T> node) {
 2         AvlNode<T> child = node.getRight();
 3         if (child.getBf() == RH) {
 4             /* RR */
 5             node.setBf(EH);
 6             child.setBf(EH);
 7             left_Rotation(node);
 8         } else {
 9             /* RL */
10             AvlNode<T> grand = child.getLeft();
11             switch (grand.getBf()) {
12                 case RH : {
13                     node.setBf(LH);
14                     child.setBf(EH);
15                     break;
16                 }
17                 case EH : {
18                     node.setBf(EH);
19                     child.setBf(EH);
20                     break;
21                 }
22                 case LH : {
23                     node.setBf(EH);
24                     child.setBf(RH);
25                     break;
26                 }
27             }
28             grand.setBf(EH);
29             right_Rotation(child);
30             left_Rotation(node);
31         }
32     }

旋转

左旋转函数

当前结点为n， nr 为 n 的右孩子，nrl 为 nr 的左孩子，旋转设置为：将 nr 的左孩子设置为 n，将 n 的右孩子设置 nrl。

 1     private void left_Rotation(AvlNode<T> n) {
 2         /*
 3          *      n                nr
 4          *    /   \            /   \
 5          *   nl    nr   =>    n     nrr
 6          *       /   \      /   \
 7          *      nrl   nrr  nl    nrl
 8          */
 9         AvlNode<T> p = n.getParent();
10         AvlNode<T> nr = n.getRight();
11         AvlNode<T> nrl = nr.getLeft();
12         int pointer = p != null ? (p.getLeft() == n ? LEFT : RIGHT) : NONE;
13         n.setRight(nrl);
14         nr.setLeft(n);
15         if (p == null) {
16             head = nr;
17             nr.setParent(null);
18         } else if (pointer == LEFT)
19             p.setLeft(nr);
20         else
21             p.setRight(nr);
22     }

右旋转函数

当前结点 n， nl 为 n 的左孩子，nlr 为 nl 的右孩子，旋转设置：nl 的右孩子设置为 n， n 的左孩子设置为 nlr。

 1     private void right_Rotation(AvlNode<T> n) {
 2        /*
 3         *           n               nl
 4         *         /   \           /   \
 5         *       nl     nr   =>   nll   n
 6         *     /   \                   /  \
 7         *    nll  nlr                nlr  nr
 8         */
 9         AvlNode<T> p = n.getParent();
10         AvlNode<T> nl = n.getLeft();
11         AvlNode<T> nlr = nl.getRight();
12         int pointer = p != null ? (p.getLeft() == n ? LEFT : RIGHT) : NONE;
13         n.setLeft(nlr);
14         nl.setRight(n);
15 
16         if (p == null) {
17             head = nl;
18             nl.setParent(null);
19         } else if (pointer == LEFT)
20             p.setLeft(nl);
21         else
22             p.setRight(nl);
23     }

结点定义

 1 public class AvlNode <T extends Comparable<T>> {
 2     /** 数据域 */
 3     private T data;
 4     /** 父节点 */
 5     private AvlNode parent;
 6     /** 左子树根节点 */
 7     private AvlNode left;
 8     /** 右子树根节点 */
 9     private AvlNode right;
10     /** 平衡因子 */
11     private int bf;
12 
13     public AvlNode(T data) {
14         this.data = data;
15         bf = 0;
16     }
17     // 省略 getter setter
18 }

树定义

定义根节点、常量定义以及基本方法。

 1 public class AvlTree<T extends Comparable<T>> implements Tree<AvlNode<T>, T> {
 2 
 3     /** 左子树高于右子树  */
 4     private static final int LH = 1;
 5     /** 左子树和右子树相同 */
 6     private static final int EH = 0;
 7     /** 左子树低于右子树 */
 8     private static final int RH = -1;
 9     /** 左指针 */
10     private static final int LEFT = 1;
11     /** 右指针 */
12     private static final int RIGHT = 2;
13     /** 未知 */
14     private static final int NONE = 0;
15 
16     /* 比较结果 */
17     static final int QUEUE_INITIALIZE = 0x00000000;
18     static final int GRATER = 0x00000001;
19     static final int LESS = 0x00000000;
20     static final int VALID_BIT = 0x00000001;
21 
22     private AvlNode<T> head;
23 
24 }

查找元素

 1     @Override
 2     public AvlNode<T> search(T data) {
 3         if (data == null) return null;
 4         AvlNode<T> n = head;
 5         while (n != null) {
 6             int r = data.compareTo(n.getData());
 7             if (r == 0) return n;
 8             if (r < 0) n = n.getLeft();
 9             if (r > 0) n = n.getRight();
10         }
11         return null;
12     }

插入元素

插入肯定在某个叶子结点上，树的高度增加，平衡因子也要改变。需要自底向上改变平衡因子，当遇到平衡因子为 -2 和 2 时需要做相应的子树平衡，平衡后的子树高度不变，因此会终止向上回溯。

如果是空树则构建一个根节点的树。
遍历树，查找给定的元素，如果找到则插入失败否则在叶子结点上插入新结点。
从插入新结点的叶子结点向上更改平衡因子：

1. 如平衡因子改变后为 -2 或者 2 则需要进行平衡，平衡后终止回溯。
2. 如平衡因子改变后变后为 0 则意味着树的高度未变，终止回溯。
3. 如平衡因子改变后变为 -1 或者 1，意味着树的高度改变，继续向上回溯。

 1    public boolean insert(T data) {
 2         if (data == null) {
 3             return false;
 4         }
 5         AvlNode<T> n = head;
 6         if (n == null) {
 7             // 空树 构建头节点
 8             head = new AvlNode<>(data);
 9             return true;
10         }
11         AvlNode<T> next = null;
12         //查找比较结果 0 为小于 , 1 为 大于
13         int cq = QUEUE_INITIALIZE;
14         while (n != null) {
15             int r = data.compareTo(n.getData());
16             if (r == 0)  return false;
17             // 之前比较结果队列左移一位，将当前结果放置在后低位
18             cq = (cq << 1) | ((r < 0 ? LESS : GRATER) & VALID_BIT);
19             if (r < 0) {
20                 if ((next = n.getLeft()) == null) {
21                     n.setLeft(new AvlNode(data));
22                     break;
23                 }
24             } else {
25                 if ((next = n.getRight()) == null) {
26                     n.setRight(new AvlNode(data));
27                     break;
28                 }
29             }
30             n = next;
31         }
32         // 逆序设置平衡因子
33         BACK_TRACE:
34         while (n != null) {
35             int r = cq & VALID_BIT;
36             if (r == LESS) {
37                 switch (n.getBf()) {
38                     case RH: n.setBf(EH); break BACK_TRACE;
39                     case EH: n.setBf(LH); break;
40                     case LH: leftBalance(n); break BACK_TRACE;
41                 }
42             } else if (r == GRATER) {
43                 switch (n.getBf()) {
44                     case RH: rightBalance(n); break BACK_TRACE;
45                     case EH: n.setBf(RH); break;
46                     case LH: n.setBf(EH); break BACK_TRACE;
47                 }
48             }
49             n = n.getParent();
50             cq = cq >> 1;
51         }
52         return true;
53     }

删除元素

任何删除非叶子结点都可转为对叶子结点的删除，因为非叶子结点，可以用该结点的直接前驱（左子树的最右结点）或者直接后继（右子树的最左结点）来替换，因此只考虑对叶子结点的删除即可。删除后，会出现树的高度变化，这时候需要进行平衡因子的重置以及树的再次平衡。

 1     public void remove(T data) {
 2         AvlNode<T> node = head;
 3         if (node == null) return;
 4         int cq = QUEUE_INITIALIZE;
 5         AvlNode<T> d = null;
 6         /* 查找到要删除的结点 */
 7         while (node != null) {
 8             int r = data.compareTo(node.getData());
 9             if (r == 0) {
10                 d = node;
11                 break;
12             }
13             //指向结果入队
14             cq = (cq << 1) | ((r < 0 ? LESS : GRATER) & VALID_BIT);
15             if (r < 0)
16                 node = node.getLeft();
17             else
18                 node = node.getRight();
19         }
20         if (d == null) return; /* NOT FOUND */
21         /* 将待删除结点赋值给 node 变量，寻找右子树最小值结点或者左子树最大值结点，即 d 的直接前驱或者直接后继*/
22         node = d;
23         int pointer = NONE;
24         AvlNode<T> next = null;
25         if ((next = node.getRight()) == null) {
26             if ((next = node.getLeft()) != null) {
27                 pointer = LEFT;
28                 cq = (cq << 1) | (LESS & VALID_BIT);
29             }
30         } else {
31             cq = (cq << 1) | (GRATER & VALID_BIT);
32             pointer = RIGHT;
33         }
34         //next == null 说明 d 就是叶子结点
35         if (next != null) {
36             node = next;
37             while (true) {
38                 if (pointer == RIGHT) {
39                     if ((next = node.getLeft()) != null)
40                         cq = (cq << 1) | (LESS & VALID_BIT);
41                 } else {
42                     if ((next = node.getRight()) != null)
43                         cq = (cq << 1) | (GRATER & VALID_BIT);
44                 }
45                 if (next == null) break;
46                 node = next;
47             }
48         }
49         if (d != node) d.setData(node.getData());
50         AvlNode<T> p = node.getParent();
51         if (p == null) {
52             /* 根结点直接置空树 */
53             head = null;
54             return;
55         }
56 
57         //逆序设置平衡因子 并再次平衡子树,
58         node = p;
59         int dr = cq & VALID_BIT;
60         BACK_TRACE:
61         while (node != null) {
62             int r = cq & VALID_BIT;
63             int bf = node.getBf();
64             next = node.getParent();
65             if (r == LESS) {
66                 /* 左子树高度减少  */
67                 switch (bf) {
68                     /** 高度减少 继续回溯 */
69                     case LH: node.setBf(EH); break;
70                     /** 高度无变化,结束回溯 */
71                     case EH: node.setBf(RH); break BACK_TRACE;
72                     /** 左子树高度减少,右子树变高，进行右子树平衡,平衡后高度会减少，继续向上回溯 */
73                     case RH: rightBalance(node); break;
74                 }
75             } else {
76                 /* 右子树高度减少 */
77                 switch (bf) {
78                     /** 右子树高度减少,左子树变高, 进行左子树平衡，平衡后高度减少继续向上回溯 */
79                     case LH: leftBalance(node); break;
80                     /** 子树高度无变化，终止回溯 */
81                     case EH: node.setBf(LH); break BACK_TRACE;
82                     /** 右子树高度减少, 继续向上回溯 */
83                     case RH: node.setBf(EH); break;
84                 }
85             }
86             cq = cq >> 1;
87             node = next;
88         }
89 
90         /* 切断删除的叶子结点 */
91         if (dr == LESS)
92             p.setLeft(null);
93         else
94             p.setRight(null);
95 
96     }

posted @ 2023-04-01 11:55 茄菲兔阅读(23) 评论(0) 编辑收藏举报

刷新页面返回顶部

茄菲兔的学习家园

学无止境，逆水行舟，不进则退！！！