异或线性基
异或线性基
我们先从线性基的基本问题开始。
给定一个数组 \(A = [a_1, a_2, a_3, \dots, a_n]\),其中 \(a_i \le 2 ^ d\),在 \(A\) 中选择某个子集,将其中的所有元素异或,求出可以得到的数字的个数。
考虑一个简单的做法,我们用一个集合 \(S\) 表示当前可以凑出来的所有元素,那么,对于每一个 \(a_i\),我们将 \(S\) 中的每一个元素与 \(a_i\) 异或后的结果加入到 \(S\) 中,最终答案就是 \(S\) 的大小。
这样,我们就有了一个 \(O(n \times 2 ^ d)\) 的做法。
我们需要研究一下 \(S\) 的性质,假设 \(x, y\) 是 \(S\) 中的两个元素,那么,显然的 \(x \oplus y\) 也存在与 \(S\) 中。
因为我们可以将凑出 \(x\) 的每一个元素与凑出 \(y\) 的每一个元素组合起来,凑出 \(x \oplus y\)。
即使凑出 \(x, y\) 用到了相同的元素也没关系,因为两个相同的数异或是等于 \(0\) 的,也就是没有贡献,可以直接丢掉。
因此,我们假设 \(x\) 是 \(S\) 中的某个元素,\(y\) 不是 \(S\) 中的某个元素,那么 \(x \oplus y\) 肯定也不是 \(S\) 中的元素。
因为如果 \(x \oplus y\) 是 \(S\) 中的元素,我们就可以将凑出 \(x\) 的方案和凑出 \(x \oplus y\) 的方案组合到一起,凑出 \(y\)。
因此,我们可以得出一个做法:
对于每一个 \(a_i\),判断 \(a_i\) 是否存在与 \(S\) 中,如果不存在,就将 \(S\) 中的所有元素与 \(a_i\) 异或,再加入 \(S\) 中。
显然的,每次我们的集合大小都会翻倍,也就是说,最多只会加倍 \(d\) 次。
这样的时间复杂度是 \(O(n + 2 ^ d)\)。
但是,如果 \(2 ^ d\) 很大,这样是不行的,因为我们无法存储 \(S\),这意味着我们需要压缩 \(S\)。
这时候,集合的大小最多只会加倍 \(d\) 次是十分重要的,我们可以只存储让集合大小翻倍的那些 \(a_i\) 即可。
但是,接下来又有一个问题:我们要如何判断当前的 \(a_i\) 是否可以被凑出来呢?
我们可以发现,我们所存储的这些 \(a_i\) 是可以进行某些变换的。
加入当前我们存储了 \(x, y\) 两个元素,我们把这两个元素变成 \(x, x \oplus y\) 也是不会影响这个集合所能凑出的元素的。
又由于我们最多只会存储 \(d\) 个元素,因此,我们可以考虑每一个元素管辖一位。
也就是说,我们假设存储的 \(b_i\) 的二进制表示下的最高位为 \(c_i\),那么,我们需要使得整个 \(b\) 数组的所对应的 \(c\) 数组中的元素互不相同。
我们每一次可以将 \(c_i\) 相等的所有数字,也就是 \(x_1, x_2, x_3, \dots, x_k\),把 \(x_2, x_3, \dots, x_k\) 全部异或上 \(x_1\),这样每一个 \(b_i\) 所对应的 \(c_i\) 就都是互不相同的了。
这样,时间复杂度就是 \(O(n \times d)\) 或 \(O(n \times d \log d)\) 的。
int F(ll x) {
for (int i = 49; i >= 0; i--) {
if (x & (1ll << i)) return i;
}
}
struct matrix {
ll b[55];
ll Check(ll x) {
for (int k = 49; k >= 0; k--) {
if (x & (1ll << k)) x ^= b[k];
}
return x;
}
void Insert(ll x) {
ll tp = Check(x), t = 0;
if (tp) t = F(tp);
else return ;
while (b[t]) tp ^= b[t], t = F(tp);
b[t] = tp;
}
};
其实感觉有点像 abc 236 f 的时间复杂度的证明。
abc 141 f
题意
给定 \(n\) 个非负整数 \(a_1, a_2, \dots, a_n\),将这些数分为 \(A, B\) 两个集合(不能为空),使得 \(A\) 集合内元素异或值加上 \(B\) 集合内元素异或值最大。
求出最大值。
思路
我们假设当前分到 \(A\) 集合中的数的异或值为 \(x\),所有数的异或值为 \(y\)。
那么,我们就是要求出 \(x + (x \oplus y)\) 的最大值。
我们考虑 \(y\) 的每一位,假设当前是第 \(i\) 位:
- 如果当前这一位为 \(1\),那么 \(x\) 的这一位无论是 \(1\),还是 \(0\),\(x, x \oplus y\) 的这一位的总和都是 \(1\),也就是说这一位的贡献永远是 \(2 ^ i\)。
- 如果当前这一位为 \(0\),那么,我们肯定希望 \(x, x \oplus y\) 在这一位都是 \(1\),但是,显然的,我们很难做到让这样的每一位的贡献都是 \(2 \times 2 ^ i\)。
所以,我们只考虑 \(y\) 为 \(0\) 的每一位,求出这些位的异或最大值。
代码
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5 + 10;
int n, m;
ll a[N], s, b[N], ans;
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i], s ^= a[i];
for (int i = 1; i <= n; i++) {
ll x = a[i] & (s ^ ((1ll << 60) - 1));
sort(b + 1, b + m + 1);
for (int j = m, k = 60; j >= 1; ) {
for (; k >= 0 && !(b[j] >> k); k--);
ll t = b[j];
for (j--; j >= 1 && (b[j] >> k) == 1; b[j] ^= t, j--);
}
sort(b + 1, b + m + 1);
for (int k = 60, j = m; k >= 0; k--) {
if (x & (1ll << k)) {
for (; j >= 1 && (b[j] >> k) > 1; j--);
if ((b[j] >> k) == 1) x ^= b[j];
}
}
if (x) b[++m] = x;
}
sort(b + 1, b + m + 1);
for (int i = 60, j = m; i >= 0; i--) {
if (ans & (1ll << i)) continue;
for (; j >= 1 && (b[j] >> i) > 1; j--);
if ((b[j] >> i) == 1) ans ^= b[j];
}
cout << ans + (s ^ ans);
return 0;
}
CF1902F
题意
给定一颗包含 \(n\) 个结点的树,每个点有一个点权 \(a_i\)。
有 \(q\) 次询问,每次查询给出 \(x, y, k\),请你判断 \(x\) 到 \(y\) 的路径上是否可以选出一个子集,使得子集的异或和为 \(k\)。
思路
我们首先得明确一个点:线性基是可以直接合并的。
所以,我们可以每次求出 lca,在求出 lca 的过程中将线性基的倍增数组合并即可。
但是这样常数太大了,所以我们可以用类似于 ST 表的方式求出答案。

对于这样的一条链,我们可以把它拆分为两个部分:
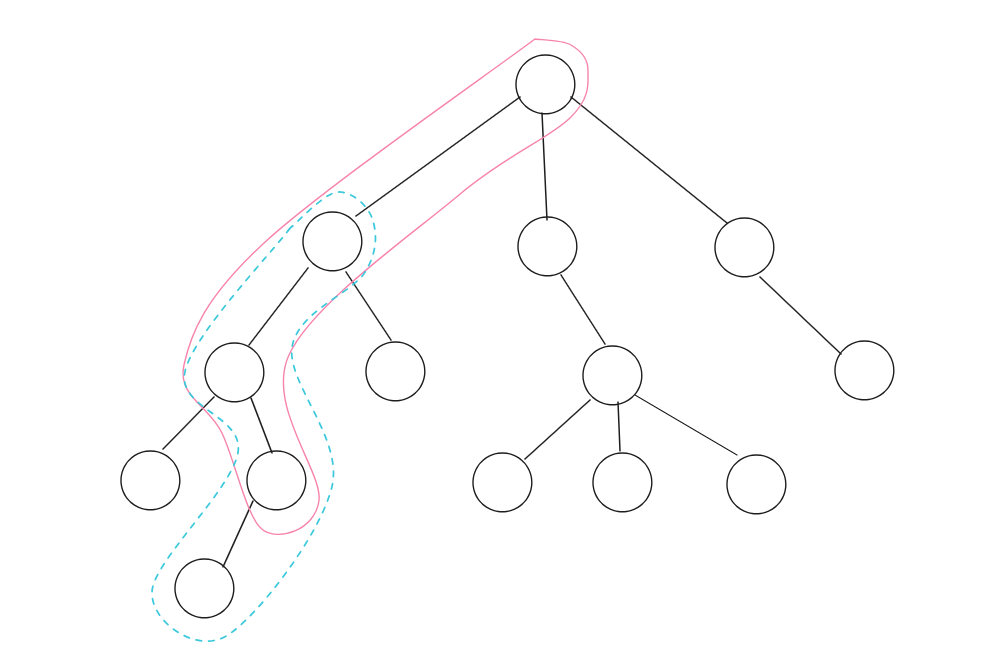
像这样查询即可,时间复杂度为 \(O(q \log ^ 3 n)\)。
代码
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 2e5 + 10;
int fir[1 << 20];
struct matrix {
int b[25];
int Check(int x) {
for (int k = 19; k >= 0; k--) {
if (x & (1 << k)) x ^= b[k];
}
return x;
}
void Insert(int x) {
int tp = Check(x), t = 0;
if (tp) t = fir[tp];
else return ;
while (b[t]) tp ^= b[t], t = fir[tp];
b[t] = tp;
}
} tr[N][18], Empty;
int n, a[N], fa[N][18], q, dep[N], Log[N];
vector<int> g[N];
void dfs(int u, int fx) {
tr[u][0] = Empty, tr[u][0].Insert(a[u]);
fa[u][0] = fx, dep[u] = dep[fx] + 1;
for (int v : g[u]) {
if (v != fx) dfs(v, u);
}
}
matrix Merge(matrix x, matrix y) {
for (int i = 0; i < 20; i++) x.Insert(y.b[i]);
return x;
}
inline int lowbit(int x) {
return x & (-x);
}
int Find(int x, int k) {
while (k) x = fa[x][Log[lowbit(k)]], k -= lowbit(k);
return x;
}
int Lca(int x, int y) {
if (dep[x] < dep[y]) swap(x, y);
x = Find(x, dep[x] - dep[y]);
if (x == y) return x;
for (int i = 17; i >= 0; i--) {
if (fa[x][i] != fa[y][i]) {
x = fa[x][i], y = fa[y][i];
}
}
return fa[x][0];
}
matrix query(int x, int y) {
int p = Log[dep[x] - dep[y] + 1];
return Merge(tr[x][p], tr[Find(x, dep[x] - dep[y] + 1 - (1 << p))][p]);
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 2; i <= n; i++) Log[i] = Log[i / 2] + 1;
for (int i = 0; i < (1 << 20); i++) {
for (int j = 19; j >= 0; j--) {
if (i & (1 << j)) {
fir[i] = j; break;
}
}
}
fill(Empty.b, Empty.b + 25, 0);
for (int i = 1, u, v; i < n; i++) {
cin >> u >> v;
g[u].push_back(v), g[v].push_back(u);
}
dfs(1, 0);
for (int i = 1; i < 18; i++) {
for (int j = 1; j <= n; j++) {
fa[j][i] = fa[fa[j][i - 1]][i - 1];
tr[j][i] = Merge(tr[j][i - 1], tr[fa[j][i - 1]][i - 1]);
}
}
cin >> q;
while (q--) {
int x, y, k; cin >> x >> y >> k;
int t = Lca(x, y);
matrix ans = Merge(query(x, t), query(y, t));
cout << (ans.Check(k) ? "NO\n" : "YES\n");
}
return 0;
}


