abc 232 e 题解
abc 232 e
题意#
有一个
有
请你求出在 998244353 取模。
思路#
首先,这道题我们先考虑暴力。
那么就有转移:
所以,状态总数为
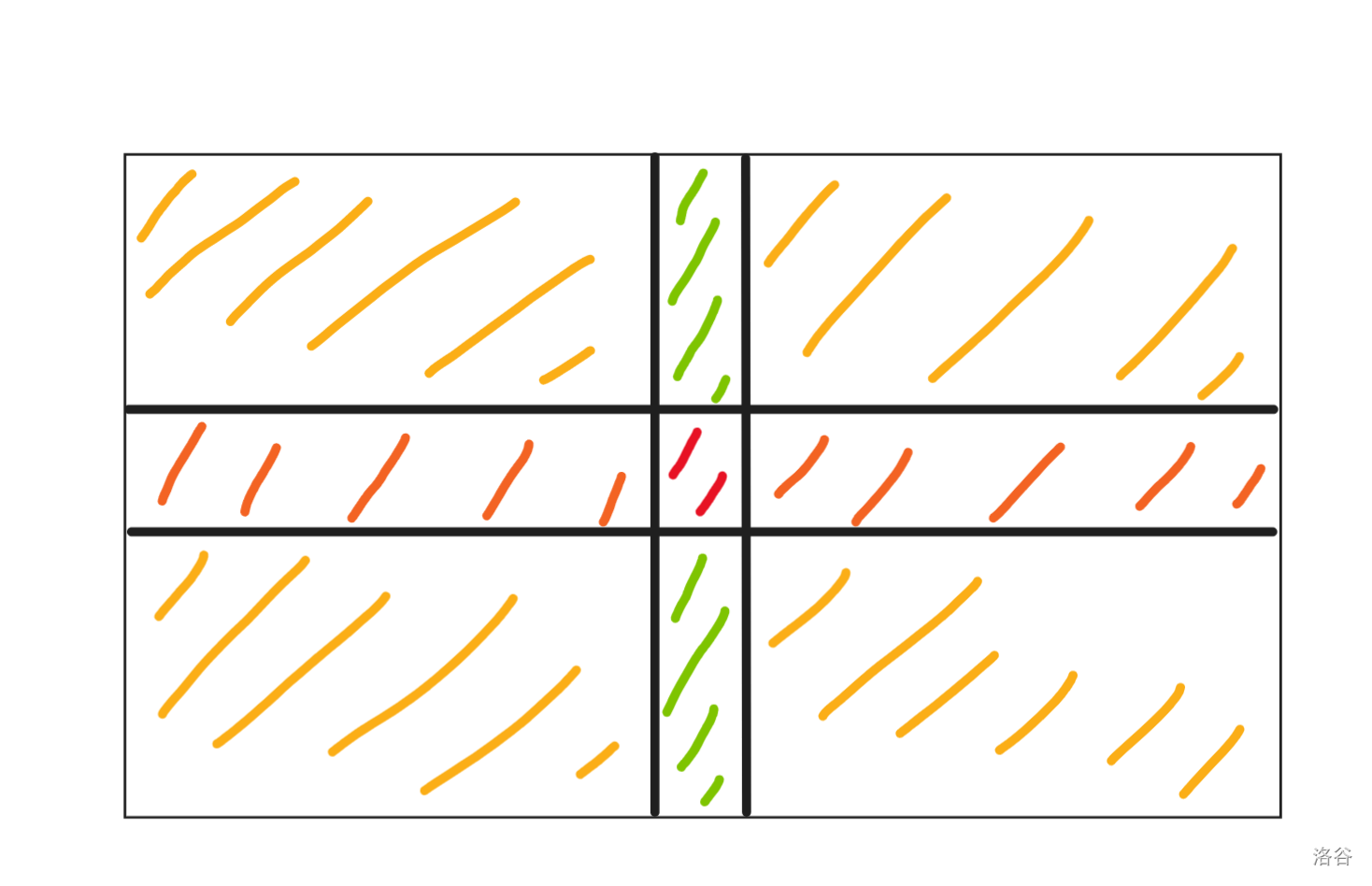
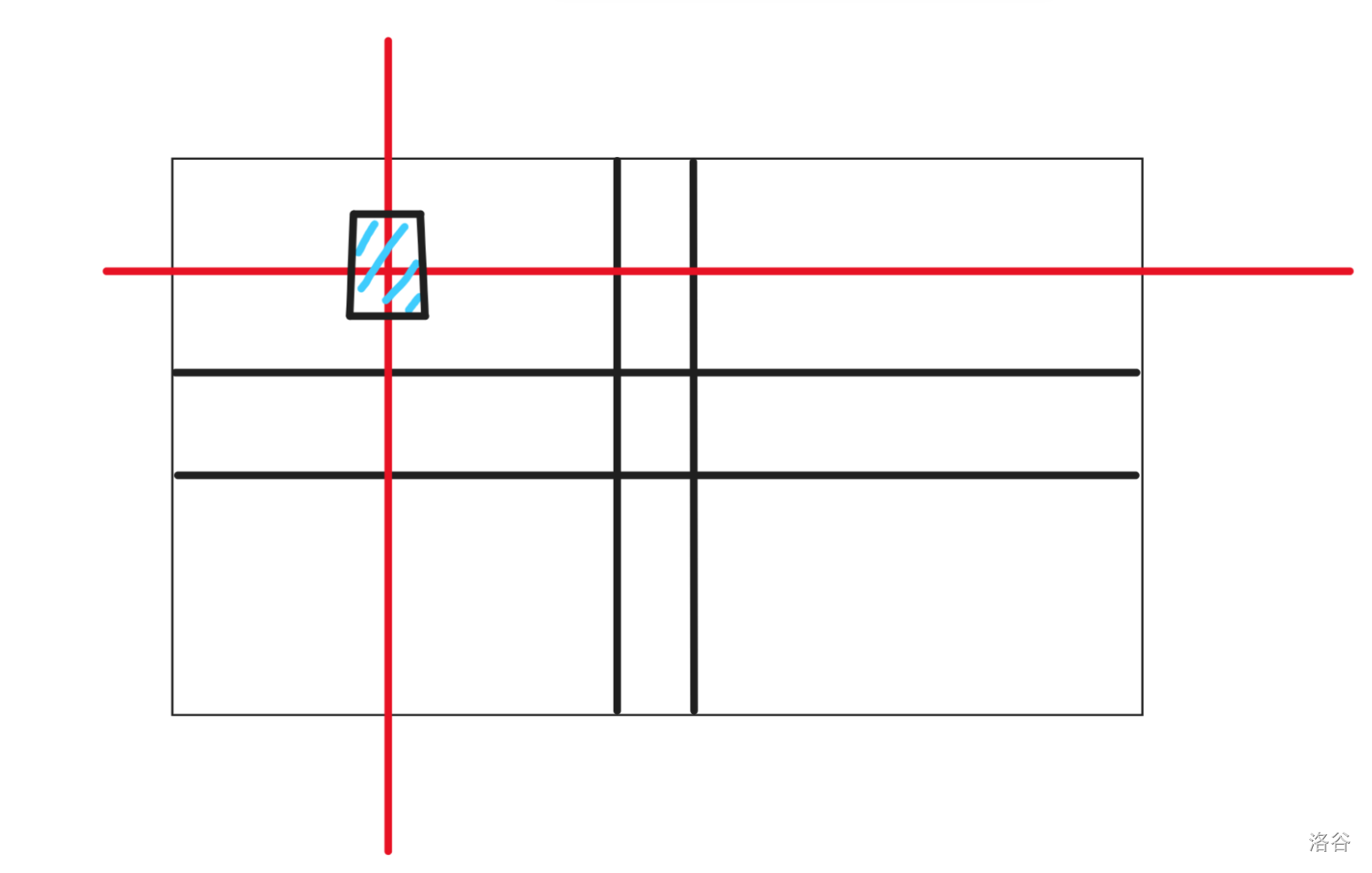
通过打表输出 dp 数组,我们可以发现,整个矩阵最后的结果一共可以分为四种:
-
起点
-
和起点同行的点
-
和起点同列的点
-
和起点不同行也不同列的点
所以,
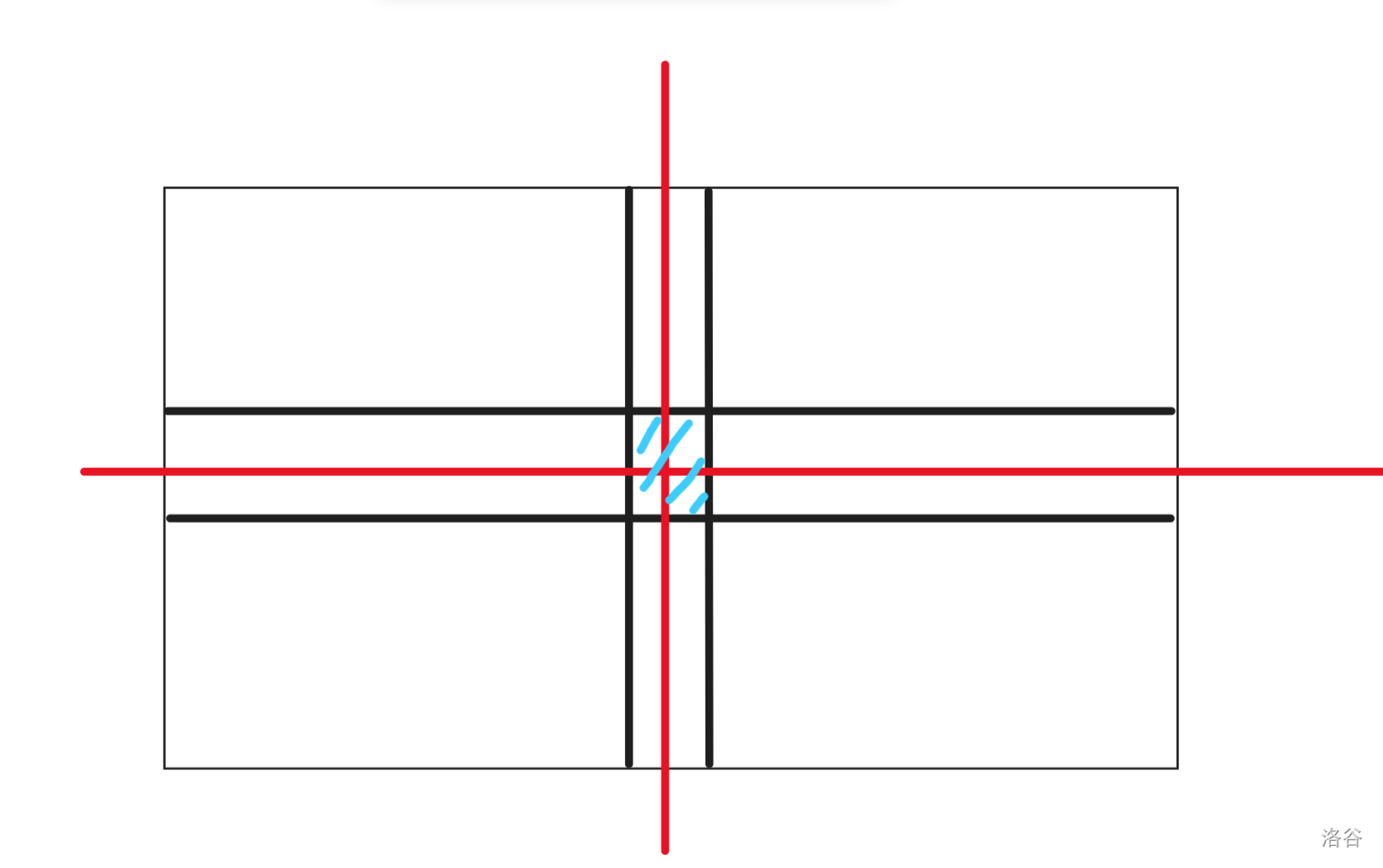
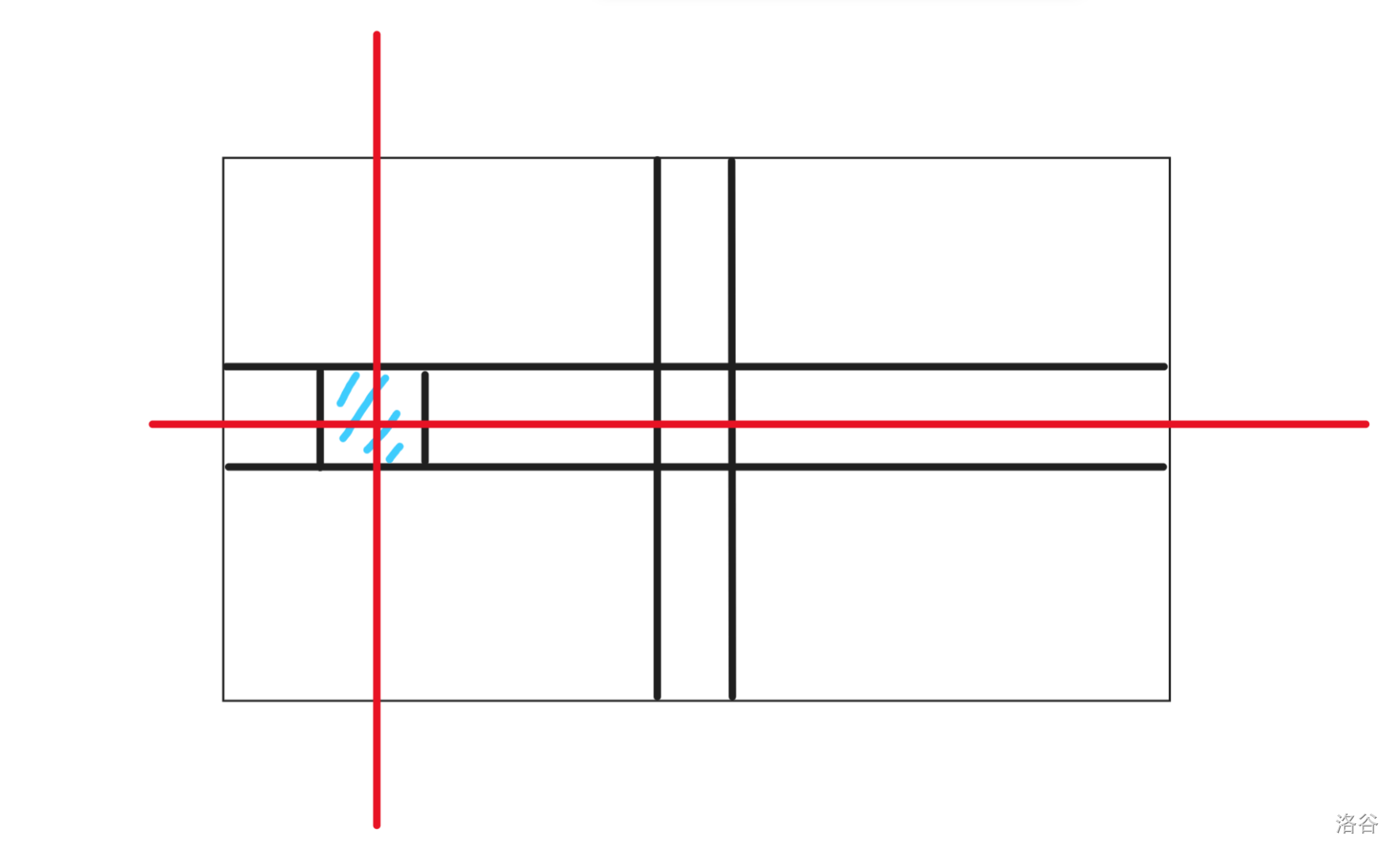
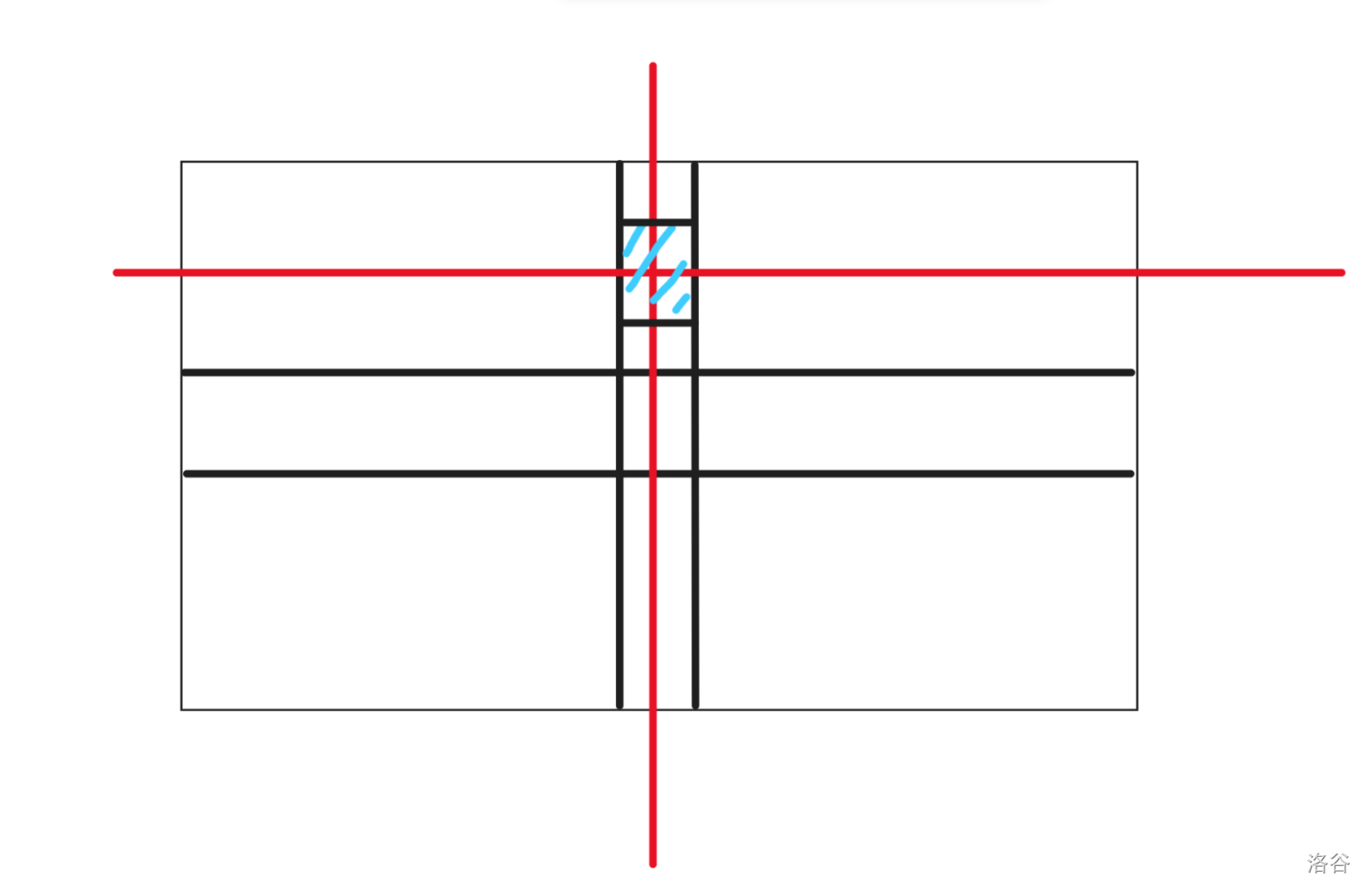
那么,转移是什么呢?
我们可以画一个图来看一看。
所以,时间复杂度为
作者:cn
出处:https://www.cnblogs.com/chengning0909/p/18422873
版权:本作品采用「署名-非商业性使用-相同方式共享 4.0 国际」许可协议进行许可。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 单线程的Redis速度为什么快?
· SQL Server 2025 AI相关能力初探
· AI编程工具终极对决:字节Trae VS Cursor,谁才是开发者新宠?
· 展开说说关于C#中ORM框架的用法!
2023-09-20 线性代数