线段树分治
线段树分治
例题 ：Gym - 100551A
题意
有一张包含 \(n\) 个点的图，最开始图是空的。
给定 \(k\) 次询问，询问有三种类型：
- 向图中添加一条边
- 从图中删去一条边
- 计算连通块数量
思路
很显然的，我们无法用暴力解决这个问题。
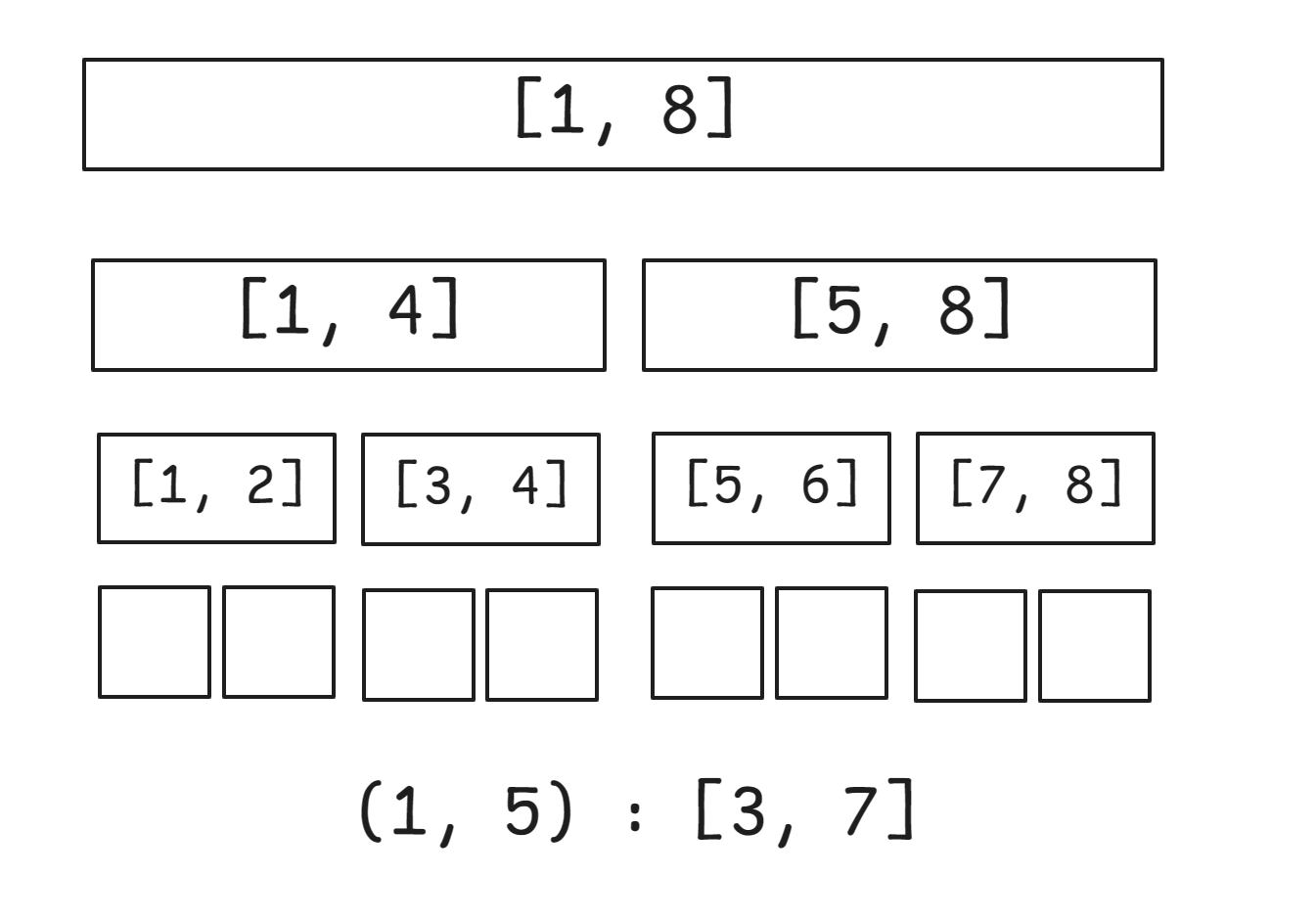
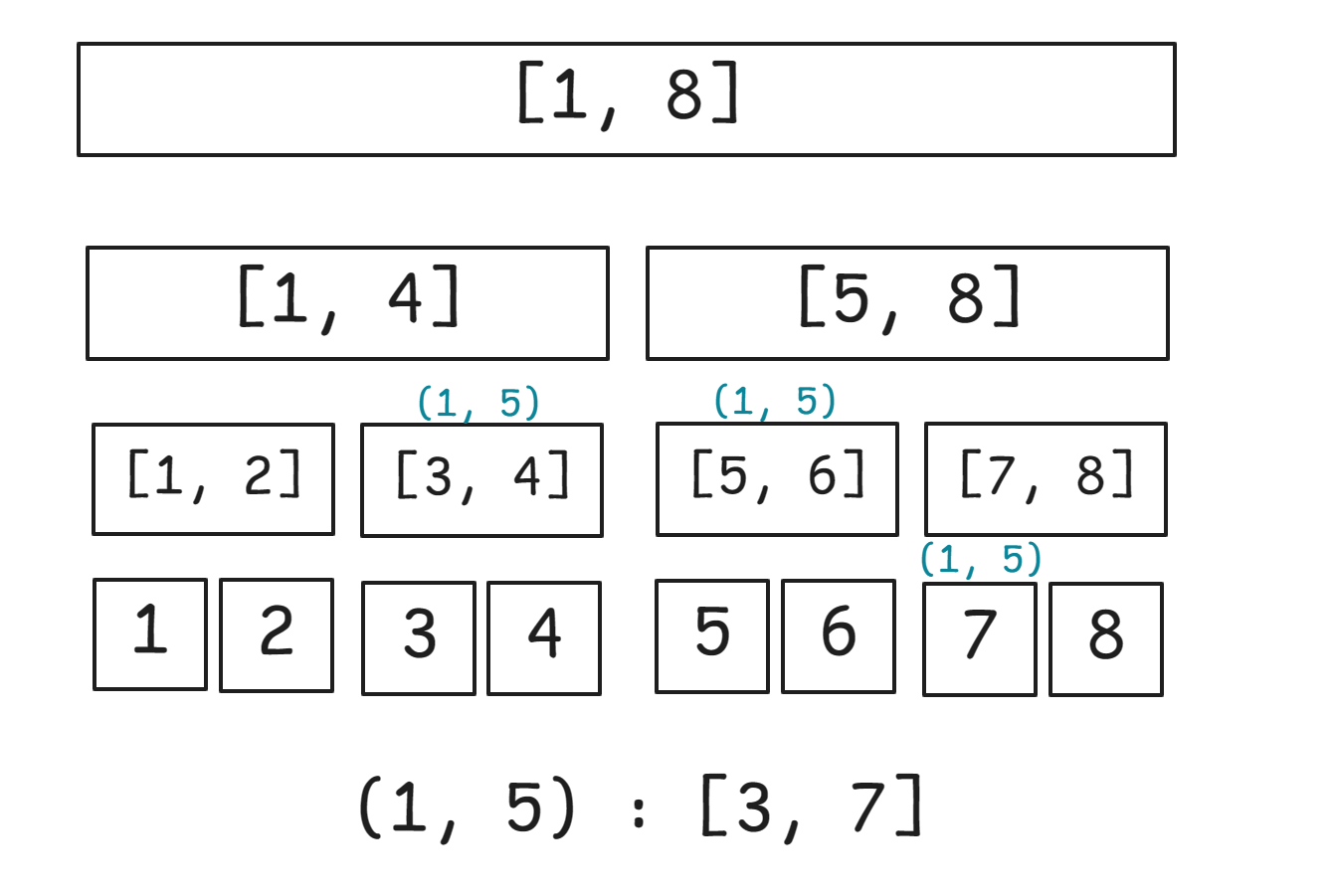
我们会发现，每一条边在图中存在的时间肯定是一个区间，因此，我们对时间轴建线段树。
也就是说，对于每一条边所出现的时间区间 \([l, r]\)，我们把这条边加入这个区间所对应的线段树上的结点。
然后，我们考虑递归遍历线段树的方式解决查询。
我们考虑在区间 \([3, 7]\) 加入 \((1, 5)\) 这条边，也就是：
当我们遍历线段树时，每遍历到一个结点，我们就将这个结点上的每一条边都加入并查集。
然后，我们需要遍历这个结点的左子树和右子树。
当我们需要退出这个结点时，我们就用可撤销化并查集将每一条加入的边撤销掉。
需要注意当边没有贡献时是不需要撤销的。
代码
#include <bits/stdc++.h>
using namespace std;
using pii = pair<int, int>;
const int N = 3e5 + 10;
int n, q, c, top, fa[N], sz[N], ans;
int appear[N];
bool f[4 * N], vis[N];
pii edge[N], stk[N];
vector<int> tr[4 * N];
map<pii, int> mp;
void Modify(int i, int l, int r, int pos) {
if (l == r) {
f[i] = 1; return ;
}
int mid = (l + r) >> 1;
pos <= mid ? Modify(i * 2, l, mid, pos) : Modify(i * 2 + 1, mid + 1, r, pos);
}
void modify(int i, int l, int r, int ql, int qr, int x) {
if (qr < l || ql > r) return ;
if (ql <= l && r <= qr) {
tr[i].push_back(x); return ;
}
int mid = (l + r) >> 1;
modify(i * 2, l, mid, ql, qr, x), modify(i * 2 + 1, mid + 1, r, ql, qr, x);
}
int Find(int x) {
return fa[x] ? Find(fa[x]) : x;
}
void Merge(int x, int y) {
x = Find(x), y = Find(y);
if (x == y) {
stk[++top] = {0, 0}; return ;
}
if (sz[x] > sz[y]) swap(x, y);
fa[x] = y, sz[y] += sz[x];
stk[++top] = {x, y}, ans--;
}
void Cancel() {
auto [x, y] = stk[top--];
if (!x && !y) return ;
fa[x] = 0, sz[y] -= sz[x], ans++;
}
void query(int i, int l, int r) {
for (int x : tr[i]) Merge(edge[x].first, edge[x].second);
if (l == r) {
if (f[i]) cout << ans << '\n';
for (int j = 1; j <= tr[i].size(); j++) Cancel();
return ;
}
int mid = (l + r) >> 1;
query(i * 2, l, mid), query(i * 2 + 1, mid + 1, r);
for (int j = 1; j <= tr[i].size(); j++) Cancel();
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
freopen("connect.in", "r", stdin);
freopen("connect.out", "w", stdout);
cin >> n >> q, ans = n;
fill(sz + 1, sz + n + 1, 1);
if (!q) return 0;
for (int i = 1, u, v; i <= q; i++) {
char op; cin >> op;
if (op == '?') Modify(1, 1, q, i);
else {
cin >> u >> v;
if (op == '+') {
mp[{u, v}] = mp[{v, u}] = ++c, appear[c] = i, edge[c] = {u, v};
} else {
int k = mp[{u, v}];
vis[k] = 1, modify(1, 1, q, appear[k], i - 1, k);
mp[{u, v}] = mp[{v, u}] = 0;
}
}
}
for (int i = 1; i <= c; i++) if (!vis[i]) modify(1, 1, q, appear[i], q, i);
query(1, 1, q);
return 0;
}
洛谷 P5787
题意
给定一个包含 \(n\) 个结点的图，一共有 \(k\) 个时刻，\(m\) 条边，第 \(i\) 条边会在时间 \([l_i, r_i]\) 出现。
请你判断对于每个时刻，这个图是否是二分图。
思路
首先，我们先考虑如何判断一张图是否是二分图。
我们可以考虑使用那种 “敌人的敌人是朋友” 的方式判断，也就是说，我们考虑使用种类并查集维护。
那么，显然的，当存在点 \(u\) 使得 \(u\) 和 \(u + n\) 在同一个集合时，这张图就不是二分图。
其余的部分就还是用线段树分治的方式维护即可。
代码
#include <bits/stdc++.h>
using namespace std;
using pii = pair<int, int>;
const int N = 1e5 + 10, M = 2e5 + 10;
int n, m, k, top, fa[2 * N], sz[2 * N], ans;
bool f[N];
pii stk[2 * M];
vector<pii> tr[4 * N];
void modify(int i, int l, int r, int ql, int qr, int u, int v) {
if (qr < l || ql > r) return ;
if (ql <= l && r <= qr) {
tr[i].push_back({u, v}); return ;
}
int mid = (l + r) >> 1;
modify(i * 2, l, mid, ql, qr, u, v), modify(i * 2 + 1, mid + 1, r, ql, qr, u, v);
}
int Find(int x) {
return fa[x] ? Find(fa[x]) : x;
}
void Merge(int x, int y) {
x = Find(x), y = Find(y);
if (x == y) {
stk[++top] = {0, 0}; return ;
}
if (sz[x] > sz[y]) swap(x, y);
fa[x] = y, sz[y] += sz[x];
stk[++top] = {x, y};
}
void Cancel() {
auto [x, y] = stk[top--];
if (!x && !y) return ;
fa[x] = 0, sz[y] -= sz[x];
}
void query(int i, int l, int r) {
for (auto [u, v] : tr[i]) {
ans -= Find(u) == Find(u + n);
Merge(u + n, v), Merge(u, v + n);
ans += Find(u) == Find(u + n);
}
if (l == r) {
if (l < k) cout << (!ans ? "Yes\n" : "No\n");
for (int j = tr[i].size() - 1; j >= 0; j--) {
auto [u, v] = tr[i][j];
ans -= Find(u) == Find(u + n);
Cancel(), Cancel();
ans += Find(u) == Find(u + n);
}
return ;
}
int mid = (l + r) >> 1;
query(i * 2, l, mid), query(i * 2 + 1, mid + 1, r);
for (int j = tr[i].size() - 1; j >= 0; j--) {
auto [u, v] = tr[i][j];
ans -= Find(u) == Find(u + n);
Cancel(), Cancel();
ans += Find(u) == Find(u + n);
}
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m >> k;
fill(sz + 1, sz + 2 * n + 1, 1);
for (int i = 1, u, v, l, r; i <= m; i++) {
cin >> u >> v >> l >> r;
if (l != r) modify(1, 0, k, l, r - 1, u, v);
}
query(1, 0, k);
return 0;
}
洛谷 P4219
题意
给定一张包含 \(n\) 个点的树，这棵树上的边是一条一条添加上去的。
每一个时刻，树上某条边的负载就是它所在的当前能够联通的树上路过它的简单路径的数量。
随着边的添加，动态的回答小强对于某些边的负载的询问。
思路
我们很容易发现，边 \((u, v)\) 的负载，就是 \(u\) 所在连通块的点的个数乘上 \(v\) 所在的连通块的点的个数。
直接把每一条边加入到线段树中，线段树分治即可。
代码
#include <bits/stdc++.h>
using namespace std;
using pii = pair<int, int>;
const int N = 1e5 + 10;
int n, q, c, top, fa[N], sz[N];
int appear[N];
pii edge[N], stk[N], que[4 * N];
vector<int> tr[4 * N];
map<pii, int> mp;
void Modify(int i, int l, int r, int pos, int u, int v) {
if (l == r) {
que[i] = {u, v}; return ;
}
int mid = (l + r) >> 1;
pos <= mid ? Modify(i * 2, l, mid, pos, u, v) : Modify(i * 2 + 1, mid + 1, r, pos, u, v);
}
void modify(int i, int l, int r, int ql, int qr, int x) {
if (qr < l || ql > r) return ;
if (ql <= l && r <= qr) {
tr[i].push_back(x); return ;
}
int mid = (l + r) >> 1;
modify(i * 2, l, mid, ql, qr, x), modify(i * 2 + 1, mid + 1, r, ql, qr, x);
}
int Find(int x) {
return fa[x] ? Find(fa[x]) : x;
}
void Merge(int x, int y) {
x = Find(x), y = Find(y);
if (x == y) {
stk[++top] = {0, 0}; return ;
}
if (sz[x] > sz[y]) swap(x, y);
fa[x] = y, sz[y] += sz[x];
stk[++top] = {x, y};
}
void Cancel() {
auto [x, y] = stk[top--];
if (!x && !y) return ;
fa[x] = 0, sz[y] -= sz[x];
}
void query(int i, int l, int r) {
for (int x : tr[i]) Merge(edge[x].first, edge[x].second);
if (l == r) {
auto [u, v] = que[i];
if (u && v) cout << 1ll * sz[Find(u)] * sz[Find(v)] << '\n';
for (int j = 1; j <= tr[i].size(); j++) Cancel();
return ;
}
int mid = (l + r) >> 1;
query(i * 2, l, mid), query(i * 2 + 1, mid + 1, r);
for (int j = 1; j <= tr[i].size(); j++) Cancel();
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> q;
fill(sz + 1, sz + n + 1, 1);
fill(que, que + 4 * n + 1, pii{0, 0});
for (int i = 1, x, y; i <= q; i++) {
char op; cin >> op >> x >> y;
if (op == 'A') {
mp[{x, y}] = mp[{y, x}] = ++c, appear[c] = i, edge[c] = {x, y};
} else {
int k = mp[{x, y}];
modify(1, 1, q, appear[k], i - 1, k);
appear[k] = i + 1, Modify(1, 1, q, i, x, y);
}
}
for (int i = 1; i <= c; i++) {
if (appear[i] <= q) modify(1, 1, q, appear[i], q, i);
}
query(1, 1, q);
return 0;
}
abc308 G
题意
有一个黑板，最开始，黑板是空的。
你要处理 \(q\) 次询问，询问分为 \(3\) 种：
1 x：在黑板上写下整数 \(x\)。2 x：将整数 \(x\) 从黑板上擦除。3：查询黑板上任意两数的异或和的最小值。
思路
我们先考虑如何处理异或最小值，显然的，使用 \(01\) 字典树可以解决这个问题。
然后就是直接线段树分治即可。
代码
#include <bits/stdc++.h>
using namespace std;
using pii = pair<int, int>;
const int N = 3e5 + 10;
int n, q, id, c, top, stk[N];
int to[N], cnt[N * 32], tr[N * 32][2], ans, ct;
bool f[4 * N];
vector<int> Tr[4 * N], p[N];
map<int, int> mp;
void Modify(int i, int l, int r, int pos) {
if (l == r) {
f[i] = 1; return ;
}
int mid = (l + r) >> 1;
pos <= mid ? Modify(i * 2, l, mid, pos) : Modify(i * 2 + 1, mid + 1, r, pos);
}
void modify(int i, int l, int r, int ql, int qr, int x) {
if (qr < l || ql > r) return ;
if (ql <= l && r <= qr) {
Tr[i].push_back(x); return ;
}
int mid = (l + r) >> 1;
modify(i * 2, l, mid, ql, qr, x), modify(i * 2 + 1, mid + 1, r, ql, qr, x);
}
void Insert(int x) {
int u = 0;
for (int i = 29; i >= 0; i--) {
int p = (x >> i) & 1;
if (!tr[u][p]) tr[u][p] = ++c;
u = tr[u][p], cnt[u]++;
}
stk[++top] = x, ct++;
}
void Cancel() {
int u = 0, x = stk[top--];
for (int i = 29; i >= 0; i--) {
int p = (x >> i) & 1;
u = tr[u][p], cnt[u]--;
}
ct--;
}
int Query(int x) {
if (!ct) return 2e9;
int u = 0, ret = 0;
for (int i = 29; i >= 0; i--) {
int p = (x >> i) & 1;
if (cnt[tr[u][p]]) u = tr[u][p];
else u = tr[u][p ^ 1], ret += (1 << i);
}
return ret;
}
void query(int i, int l, int r) {
int tmp = ans;
for (int x : Tr[i]) ans = min(ans, Query(x)), Insert(x);
if (l == r) {
if (f[i]) cout << ans << '\n';
for (int j = 1; j <= Tr[i].size(); j++) Cancel();
ans = tmp;
return ;
}
int mid = (l + r) >> 1;
query(i * 2, l, mid), query(i * 2 + 1, mid + 1, r);
for (int j = 1; j <= Tr[i].size(); j++) Cancel();
ans = tmp;
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> q, ans = 2e9;
for (int i = 1, op, x; i <= q; i++) {
cin >> op;
if (op == 1) {
cin >> x;
if (!mp.count(x)) mp[x] = ++id, to[id] = x;
p[mp[x]].push_back(i);
} else if (op == 2) {
cin >> x;
int k = p[mp[x]].back(); p[mp[x]].pop_back();
modify(1, 1, q, k, i - 1, x);
} else Modify(1, 1, q, i);
}
for (int i = 1; i <= id; i++) {
for (auto x : p[i]) modify(1, 1, q, x, q, to[i]);
}
query(1, 1, q);
return 0;
}
abc308 H
题意
有一个简单的无向图，包含 \(n\) 个顶点和 \(m\) 条边。边最初被涂成白色。
第 \(i\) 条边连接 \(a_i, b_i\)，将其涂黑的代价为 \(c_i\)。
“制作一个 \(Q\)” 意味着涂黑四条或更多边，使得：
- 除了其中恰好一条涂成黑色的边外，其他涂成黑色的边形成一个简单环，并且
- 不形成简单环的那一条黑色边，连接环上的一个顶点和不在环上的另一个顶点。
确定是否可以制作一个 \(Q\)。如果可以，找出制作一个 \(Q\) 所需的最小总成本。
思路
我们枚举伸出去的那条边在环上的那个点 \(u\)，对于这个点，我们枚举它在环上与它相邻的两个点 \(v_1, v_2\)。
然后，环上的其他部分，我们就直接选择 \(v_1\) 到 \(v_2\) 的最短路，但是，这条最短路不能经过 \(u\)。
因此，我们使用线段树分治求出对于每一个 \(u\)，任意两点间不经过 \(u\) 的最短路。
然后伸出去的边就是除了 \((u, v_1), (u, v_2)\) 这两条边之外，其他边中边权最小的边。
代码
#include <bits/stdc++.h>
using namespace std;
using pii = pair<int, int>;
const int N = 310;
struct Node {
int v, w;
bool operator < (const Node &i) const {
return w < i.w;
}
};
int n, m, top, stk[N], ans;
int d[N][N], dis[N][N][N];
vector<int> tr[4 * N];
vector<Node> g[N];
void modify(int i, int l, int r, int ql, int qr, int x) {
if (qr < l || ql > r) return ;
if (ql <= l && r <= qr) {
tr[i].push_back(x); return ;
}
int mid = (l + r) >> 1;
modify(i * 2, l, mid, ql, qr, x), modify(i * 2 + 1, mid + 1, r, ql, qr, x);
}
void query(int i, int l, int r) {
vector<vector<int> > tmp(n + 1, vector<int> (n + 1));
for (int j = 1; j <= n; j++) {
for (int k = 1; k <= n; k++) tmp[j][k] = d[j][k];
}
for (int x : tr[i]) {
for (int j = 1; j <= n; j++) {
for (int k = 1; k <= n; k++) {
d[j][k] = min(d[j][k], d[j][x] + d[x][k]);
}
}
}
if (l == r) {
for (int j = 1; j <= n; j++) {
for (int k = 1; k <= n; k++) {
dis[l][j][k] = d[j][k];
}
}
for (int j = 1; j <= n; j++) {
for (int k = 1; k <= n; k++) d[j][k] = tmp[j][k];
}
return ;
}
int mid = (l + r) >> 1;
query(i * 2, l, mid), query(i * 2 + 1, mid + 1, r);
for (int j = 1; j <= n; j++) {
for (int k = 1; k <= n; k++) d[j][k] = tmp[j][k];
}
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m;
for (int i = 1; i <= n; i++) {
fill(d[i] + 1, d[i] + n + 1, 1e9);
}
while (m--) {
int u, v, w; cin >> u >> v >> w;
g[u].push_back({v, w}), g[v].push_back({u, w});
d[u][v] = d[v][u] = w;
}
for (int i = 1; i <= n; i++) sort(g[i].begin(), g[i].end());
for (int i = 1; i <= n; i++) {
modify(1, 1, n, 1, i - 1, i), modify(1, 1, n, i + 1, n, i);
}
query(1, 1, n), ans = 1e9;
for (int i = 1; i <= n; i++) {
if (g[i].size() < 3) continue;
for (int j = 0; j < g[i].size(); j++) {
for (int k = j + 1; k < g[i].size(); k++) {
int w = (!j ? (k == 1 ? g[i][2].w : g[i][1].w) : g[i][0].w);
ans = min(ans, w + g[i][j].w + g[i][k].w + dis[i][g[i][j].v][g[i][k].v]);
}
}
}
cout << (ans == 1e9 ? -1 : ans);
return 0;
}
