扫描线

扫描线，顾名思义，就是一条线在整个图上扫来扫去，它一般被用来解决图形面积，周长，以及二维数点等问题。

例题：洛谷 P5490

题意

给定 \(n\) 个在平面直角坐标系上的矩形，请你求出这些矩形的面积并。

思路

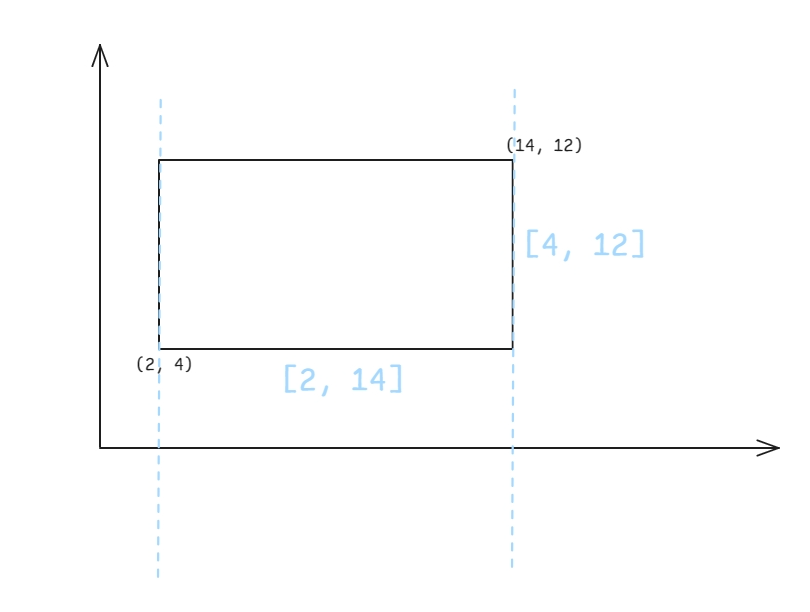
扫描线就是像上图一样算出面积并的。

我们会发现，事实上，一个矩形在坐标系中所对应的是横坐标的一段区间和纵坐标的一段区间。

我们可以考虑枚举纵坐标，然后计算出在这一行有哪些位置是被矩形覆盖的。

譬如说，当我们枚举到 \(y = 4\) 时，就将区间 \([2, 14]\) 上的数值 \(+ 1\)，枚举到 \(y = 13\) 时，就将区间 \([2, 14]\) 上的数值 \(- 1\)。

这样，对于我们枚举的每一行，我们只需要算出有多少位置的数值 \(\ge 1\) 即可。

由于每个位置的数值肯定是非负整数，所以我们可以考虑维护最小值和最小值的出现次数，当最小值为 \(0\) 时，这个答案就是坐标范围减去最小值出现次数。

注意这个题要离散化。

代码

#include <bits/stdc++.h>

using namespace std;
using ll = long long;

const int N = 2e5 + 10;

struct Node {
    int l, r;
    bool f;
};

struct SegTree {
    int mmin, cnt, lazy;
} tr[4 * N];

int n, sx[N], fx[N], sy[N], fy[N], dx[N], dy[N], cntx, cnty;
ll ans;
vector<Node> p[N];
vector<int> a, b;

void update(int i, int x) {
    tr[i].lazy += x, tr[i].mmin += x;
}

void pushdown(int i) {
    update(i * 2, tr[i].lazy), update(i * 2 + 1, tr[i].lazy);
    tr[i].lazy = 0;
}

SegTree Merge(SegTree i, SegTree j) {
    int mmin = min(i.mmin, j.mmin);
    return {mmin, (i.mmin == mmin) * i.cnt + (j.mmin == mmin) * j.cnt, 0};
}

void modify(int i, int l, int r, int ql, int qr, int x) {
    if (qr < l || ql > r) return ;
    if (ql <= l && r <= qr) {
        update(i, x); return ;
    }
    int mid = (l + r) >> 1;
    pushdown(i);
    modify(i * 2, l, mid, ql, qr, x), modify(i * 2 + 1, mid + 1, r, ql, qr, x);
    tr[i] = Merge(tr[i * 2], tr[i * 2 + 1]);
}

SegTree build(int i, int l, int r) {
    if (l == r) return tr[i] = {0, dy[r] - dy[l - 1], 0};
    int mid = (l + r) >> 1;
    return tr[i] = Merge(build(i * 2, l, mid), build(i * 2 + 1, mid + 1, r));
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0);
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> sx[i] >> sy[i] >> fx[i] >> fy[i];
        a.push_back(sx[i]), a.push_back(fx[i]);
        b.push_back(sy[i]), b.push_back(fy[i]);
    }
    sort(a.begin(), a.end());
    sort(b.begin(), b.end());
    for (int i = 0; i < a.size(); ) {
        dx[++cntx] = a[i];
        for (; i < a.size() && a[i] == dx[cntx]; i++);
    }
    for (int i = 0; i < b.size(); ) {
        dy[++cnty] = b[i];
        for (; i < b.size() && b[i] == dy[cnty]; i++);
    }
    for (int i = 1; i <= n; i++) {
        sx[i] = lower_bound(dx + 1, dx + cntx + 1, sx[i]) - dx;

        fx[i] = lower_bound(dx + 1, dx + cntx + 1, fx[i]) - dx;

        sy[i] = lower_bound(dy + 1, dy + cnty + 1, sy[i]) - dy;

        fy[i] = lower_bound(dy + 1, dy + cnty + 1, fy[i]) - dy;

        p[sx[i]].push_back({sy[i], fy[i], 0});
        p[fx[i]].push_back({sy[i], fy[i], 1});
    }
    dx[++cntx] = dy[++cnty] = 1e9, build(1, 1, cnty);
    for (int i = 1; i < cntx; i++) {
        for (Node x : p[i]) {
            if (!x.f) modify(1, 1, cnty, x.l + 1, x.r, 1);
            else modify(1, 1, cnty, x.l + 1, x.r, -1);
        }
        ans += 1ll * ((int)1e9 - (!tr[1].mmin) * tr[1].cnt) * (dx[i + 1] - dx[i]);
    }
    cout << ans;
    return 0;
}

我们考虑以横坐标为第一关键字，纵坐标为第二关键字，那么，每当我们枚举到一个点 \((x, y)\) 时，假设当前手上的答案为 \(d\)，我们就将 set 中与 \((x, y)\) 距离超过 \(d\) 的点删掉，然后枚举横坐标在 \([x - d, x]\) 中，纵坐标在 \([y - d, y + d]\) 中的未出现在 set 中的点，将他们加入 set，然后枚举 set 中的每个点，暴力更新答案。

由于我们每次选择的横坐标在 \([x - d, x]\) 中，纵坐标在 \([y - d, y + d]\) 中的点最多只有 \(6\) 个，所以可以通过。

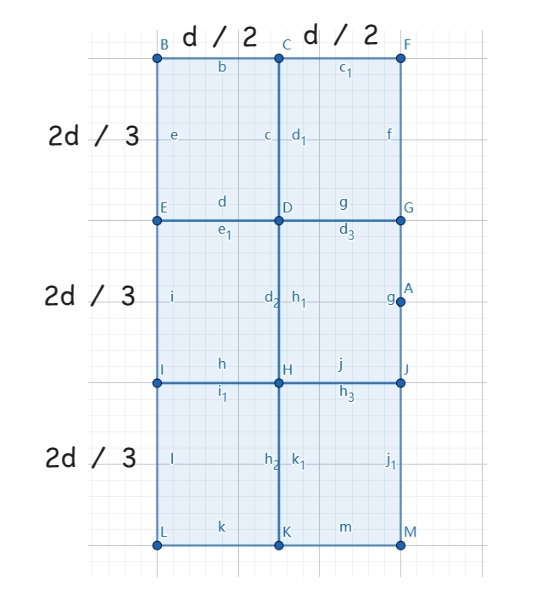
证明

\[\sqrt{\left(\frac{1}{2} \right) ^ 2 + \left(\frac{2}{3} \right) ^ 2} = \frac{5}{6} < 1 \]

我们可以将区域划分为 \(6\) 个内部最长距离小于 \(d\) 的区域（每个小区域内最多有一个点），所以可以证明每次最多扫到 \(6\) 个点。

代码

#include <bits/stdc++.h>

using namespace std;
using ll = long long;
using db = double;

const int N = 4e5 + 10;

struct Node {
    db x;
    int y, id;
    bool operator < (const Node &i) const {
        return x == i.x ? y < i.y : x < i.x;
    }
} a[N];

int n;
multiset<Node> st;

ll Dis(int i, int j) {
    return 1ll * (a[i].x - a[j].x) * (a[i].x - a[j].x) + 1ll * (a[i].y - a[j].y) * (a[i].y - a[j].y);
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0);
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i].x >> a[i].y, a[i].id = i;
    sort(a + 1, a + n + 1);
    ll ans = 9e18;
    int p = 0, q = 0;
    for (int i = 1, j = 1; i <= n; i++) {
        while (j <= n && a[j].x < a[i].x - sqrt(ans)) {
            st.erase(st.find({a[j].y, j})), j++;
        }
        auto it = st.lower_bound({a[i].y - sqrt(ans), 0});
        while (it != st.end() && (*it).x <= a[i].y + sqrt(ans)) {
            if (ans > Dis((*it).y, i)) {
                ans = Dis((*it).y, i), p = (*it).y, q = i;
            }
            it++;
        }
        st.insert({a[i].y, i});
    }
    cout << ans << '\n';
    return 0;
}

洛谷 P1502

题意

有 \(n\) 个平面直角坐标系上的点，第 \(i\) 个点的坐标是 \((x_i, y_i)\)，价值为 \(l_i\)。

你有一个大小为 \(W \times H\) 的方框，可以框住一些点，正好落在方框边缘的点是框不住的。

请你求出可以被框住的点的价值之和的最大值。

思路

我们倒着考虑，对于每个点，考虑当框的左下角落在哪个矩形时，可以框住这个点，就可以产生 \(l_i\) 的贡献。

很显然的，对于坐标为 \((x_i, y_i)\) 的一个点，当方框的左下角落在 \((x_i - W \sim x_i, y_i - H \sim y_i)\) 时，这个点就可以产生贡献。

然后，我们就可以用扫描线的方法写出这道题。

但是，需要注意的是，正好落在方框边缘的点是无法被框住的。因此，你需要对端点做一些操作，例如 \(+0.5\) 之类的。

代码

#include <bits/stdc++.h>

using namespace std;
using ll = long long;

const int N = 2e4 + 10;

struct Node {
    int l, r;
    ll x;
};

struct SegTree {
    ll mmax, lazy;
} tr[4 * N];

int T, n, cntx, cnty;
ll sx[N], fx[N], sy[N], fy[N];
ll dx[N], dy[N], w, h, light[N];
vector<Node> p[N];
vector<ll> a, b;

void update(int i, ll x) {
    tr[i].lazy += x, tr[i].mmax += x;
}

void pushdown(int i) {
    update(i * 2, tr[i].lazy), update(i * 2 + 1, tr[i].lazy);
    tr[i].lazy = 0;
}

SegTree Merge(SegTree i, SegTree j) {
    return {max(i.mmax, j.mmax), 0};
}

void modify(int i, int l, int r, int ql, int qr, ll x) {
    if (qr < l || ql > r) return ;
    if (ql <= l && r <= qr) {
        update(i, x); return ;
    }
    int mid = (l + r) >> 1;
    pushdown(i);
    modify(i * 2, l, mid, ql, qr, x), modify(i * 2 + 1, mid + 1, r, ql, qr, x);
    tr[i] = Merge(tr[i * 2], tr[i * 2 + 1]);
}

SegTree build(int i, int l, int r) {
    if (l == r) return tr[i] = {0, 0};
    int mid = (l + r) >> 1;
    return tr[i] = Merge(build(i * 2, l, mid), build(i * 2 + 1, mid + 1, r));
}

void Solve() {
    cin >> n >> w >> h, w--, h--;
    for (int i = 1, x, y; i <= n; i++) {
        cin >> x >> y >> light[i];
        sx[i] = x - w, fx[i] = x + 1;
        sy[i] = y - h, fy[i] = y;
        a.push_back(sx[i]), a.push_back(fx[i]);
        b.push_back(sy[i]), b.push_back(fy[i]);
    }
    sort(a.begin(), a.end());
    sort(b.begin(), b.end());
    for (int i = 0; i < a.size(); ) {
        dx[++cntx] = a[i];
        for (; i < a.size() && a[i] == dx[cntx]; i++);
    }
    for (int i = 0; i < b.size(); ) {
        dy[++cnty] = b[i];
        for (; i < b.size() && b[i] == dy[cnty]; i++);
    }
    for (int i = 1; i <= n; i++) {
        sx[i] = lower_bound(dx + 1, dx + cntx + 1, sx[i]) - dx;
        fx[i] = lower_bound(dx + 1, dx + cntx + 1, fx[i]) - dx;
        sy[i] = lower_bound(dy + 1, dy + cnty + 1, sy[i]) - dy;
        fy[i] = lower_bound(dy + 1, dy + cnty + 1, fy[i]) - dy;

        p[sx[i]].push_back({sy[i], fy[i], light[i]});
        p[fx[i]].push_back({sy[i], fy[i], -light[i]});
    }
    ll ans = -3e18;
    for (int i = 1; i <= cntx; i++) {
        for (Node x : p[i]) modify(1, 1, cnty, x.l, x.r, x.x);
        ans = max(ans, tr[1].mmax), p[i].clear();
    }
    cout << ans << '\n', cntx = cnty = 0;
    a.clear(), b.clear();
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0);
    cin >> T;
    while (T--) Solve();
    return 0;
}

CF269D

题意

有一堵高度为 \(t\) 的墙，墙上有 \(n\) 块木板。第 \(i\) 块木板位于高度 \(h_i\)，位于位置 \(l_i \sim r_i\)。没有两块木板共用一个点。

只有满足以下条件时，水才可以从木板 \(i\) 流到木板 \(j\)：

\(\max(l_i, l_j) < \max(r_i, r_j)\)
\(h_j < h_i\)
不存在木板 \(k\)，使得水可以从 \(i\) 流至 \(k\)，也可以从 \(k\) 流至 \(j\)。

并且，从 \(i\) 流向 \(j\) 的水流流量就是 \([l_i, r_i]\) 和 \([l_j, r_j]\) 的交集，也就是 \(\min(r_i, r_j) - \max(l_i, l_j)\)。

你需要找到一条可以从让水从墙顶流至墙底的路径，并输出最大的路径流量。

思路

我们考虑从左往右扫。

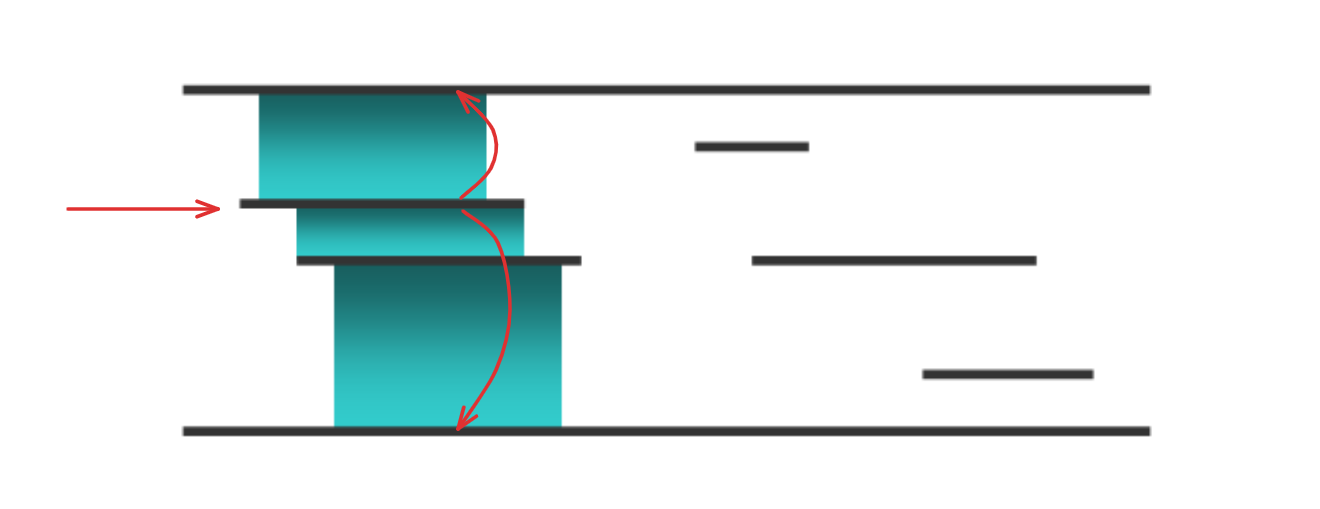
对于这张图，我们最先扫到的木板是这块：

然后，我们更新这块木板上方最近的一块木板和下方最近的一块木板，分别建边。

当我们发现有某块木板即将消失的时候，我们再更新这块木板上方最近的一块木板和下方最近的一块木板，分别建边。

像这样，我们就可以建出一个有向无环图，并且只保留的其中有用的边。

然后直接暴力的拓扑排序即可。

代码

#include <bits/stdc++.h>

using namespace std;

const int N = 2e5 + 10;

struct Node {
    int h, id;
    bool f;
    bool operator < (const Node &i) const {
        return h > i.h;
    }
};

int n, t, h[N], l[N], r[N], cnt, a[N], deg[N], f[N];
vector<Node> p[N];
set<Node> st;
map<int, bool> mp[N], vis[N];
vector<int> g[N];
queue<int> que;

void topo_sort() {
    for (int i = 0; i <= n + 1; i++) {
        if (!deg[i]) que.push(i);
    }
    while (!que.empty()) {
        int u = que.front(); que.pop();
        for (int v : g[u]) {
            if (!mp[u].count(v)) {
                if (u == n + 1) f[v] = max(f[v], r[v] - l[v]);
                else if (!v) f[v] = max(f[v], f[u]);
                else f[v] = max(f[v], min(f[u], min(r[u], r[v]) - max(l[u], l[v])));
            }
            deg[v]--;
            if (!deg[v]) que.push(v);
        }
    }
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0);
    cin >> n >> t;
    for (int i = 1; i <= n; i++) {
        cin >> h[i] >> l[i] >> r[i];
        a[++cnt] = l[i], a[++cnt] = r[i];
    }
    sort(a + 1, a + cnt + 1);
    for (int i = 1; i <= n; i++) {
        int x = lower_bound(a + 1, a + cnt + 1, l[i]) - a;
        int y = lower_bound(a + 1, a + cnt + 1, r[i]) - a;
        p[x].push_back({h[i], i, 0});
        p[y].push_back({h[i], i, 1});
    }
    st.insert({0, 0, 0}), st.insert({t, n + 1, 0});
    for (int i = 1; i <= cnt; i++) {
        sort(p[i].begin(), p[i].end(), [](Node i, Node j) {return i.f > j.f;});
        for (Node k : p[i]) {
            if (!k.f) {
                Node y = *prev(st.lower_bound({k.h, 0, 0}));
                Node x = *st.upper_bound({k.h, 0, 0});
                mp[y.id][x.id] = 1;
                if (!vis[y.id].count(k.id)) g[y.id].push_back(k.id), vis[y.id][k.id] = 1, deg[k.id]++;
                if (!vis[k.id].count(x.id)) g[k.id].push_back(x.id), vis[k.id][x.id] = 1, deg[x.id]++;
                st.insert({k.h, k.id, 0});
            } else {
                st.erase({k.h, k.id, 0});
                Node y = *prev(st.lower_bound({k.h, 0, 0}));
                Node x = *st.upper_bound({k.h, 0, 0});
                mp[y.id][x.id] = 1;
                if (!vis[y.id].count(k.id)) g[y.id].push_back(k.id), vis[y.id][k.id] = 1, deg[k.id]++;
                if (!vis[k.id].count(x.id)) g[k.id].push_back(x.id), vis[k.id][x.id] = 1, deg[x.id]++;
            }
        }
    }
    topo_sort();
    cout << f[0];
    return 0;
}

洛谷 P1856

题意

给定 \(n\) 个平面直角坐标系上的矩形，请你求出它们合并后的周长。

思路

我们将答案拆成两个部分来算，先算所有与 \(y\) 轴平行的边，再算所有与 \(x\) 轴平行的边。

我们先考虑与 \(y\) 轴平行的边。

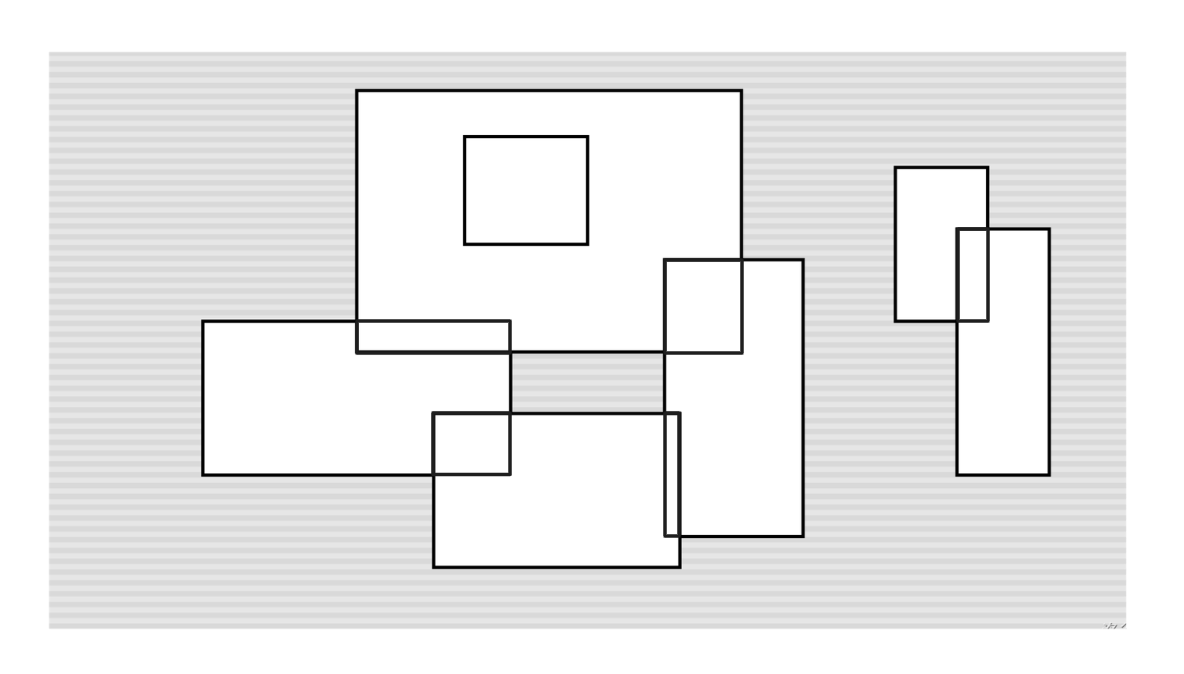
其实很显然的，我们需要算出的是那些原本在矩形上的，但是和别的矩形重叠的部分的周长和。

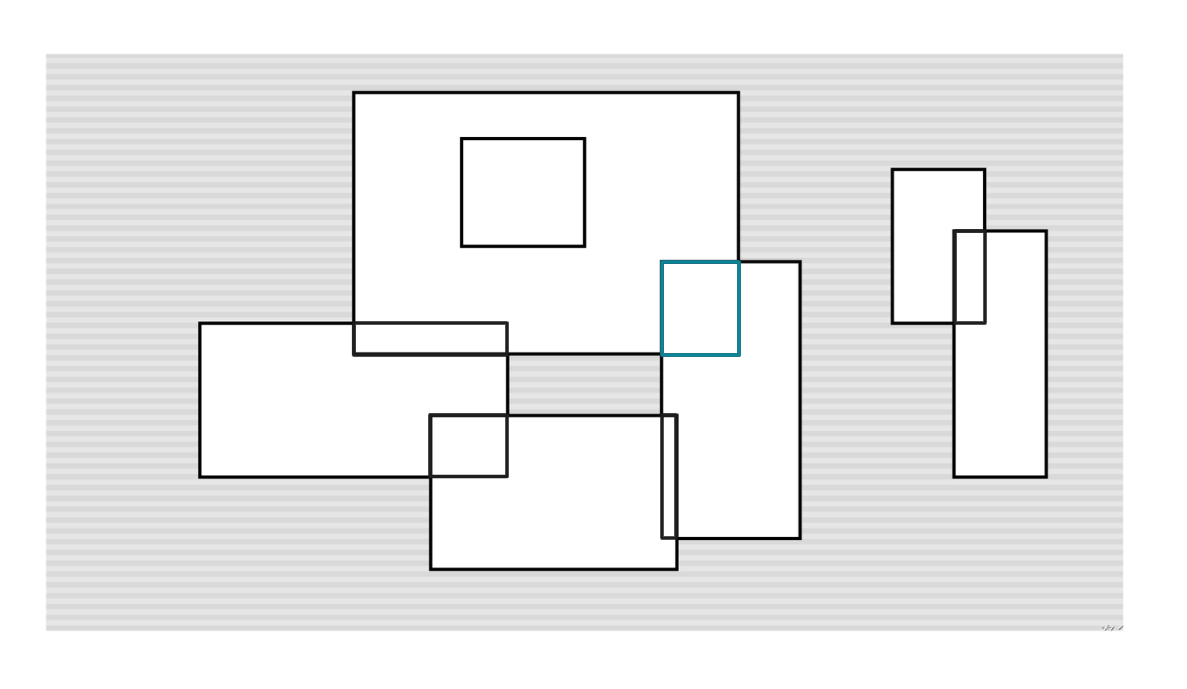
我们考虑这个青色的矩形，当我们扫到左边的边时：

我们显然会发现，在这条边的左边已经有某条线段把这段区间覆盖住了，所以，这条边对答案没有贡献。

右边的边是同样的道理。

于是我们就可以用这种方法，算两次求出答案。

代码

#include <bits/stdc++.h>

using namespace std;
using ll = long long;

const int N = 2e4 + 10, MAXN = 2e4;

struct Node {
    int l, r;
    bool f;
    bool operator < (const Node &i) const {
        return f < i.f;
    }
};

struct SegTree {
    int mmin, cnt, lazy;
} tr[4 * N];

int n;
ll ans;
vector<Node> x[N], y[N];

void update(int i, int x) {
    tr[i].lazy += x, tr[i].mmin += x;
}

void pushdown(int i) {
    update(i * 2, tr[i].lazy), update(i * 2 + 1, tr[i].lazy);
    tr[i].lazy = 0;
}

SegTree Merge(SegTree i, SegTree j) {
    int mmin = min(i.mmin, j.mmin);
    return {mmin, (i.mmin == mmin) * i.cnt + (j.mmin == mmin) * j.cnt, 0};
}

void modify(int i, int l, int r, int ql, int qr, int x) {
    if (qr < l || ql > r) return ;
    if (ql <= l && r <= qr) {
        update(i, x); return ;
    }
    int mid = (l + r) >> 1;
    pushdown(i);
    modify(i * 2, l, mid, ql, qr, x), modify(i * 2 + 1, mid + 1, r, ql, qr, x);
    tr[i] = Merge(tr[i * 2], tr[i * 2 + 1]);
}

SegTree build(int i, int l, int r) {
    if (l == r) return tr[i] = {0, 1, 0};
    int mid = (l + r) >> 1;
    return tr[i] = Merge(build(i * 2, l, mid), build(i * 2 + 1, mid + 1, r));
}

SegTree query(int i, int l, int r, int ql, int qr) {
    if (qr < l || ql > r) return {0, 0, 0};
    if (ql <= l && r <= qr) return tr[i];
    int mid = (l + r) >> 1;
    pushdown(i);
    return Merge(query(i * 2, l, mid, ql, qr), query(i * 2 + 1, mid + 1, r, ql, qr));
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0);
    cin >> n;
    for (int i = 1, x1, y1, x2, y2; i <= n; i++) {
        cin >> x1 >> y1 >> x2 >> y2;
        x1 += 1e4, x2 += 1e4, y1 += 1e4, y2 += 1e4;
        x[x1].push_back({y1 + 1, y2, 0});
        x[x2].push_back({y1 + 1, y2, 1});

        y[y1].push_back({x1 + 1, x2, 0});
        y[y2].push_back({x1 + 1, x2, 1});
    }
    build(1, 1, MAXN);
    for (int i = 0; i <= MAXN; i++) {
        sort(x[i].begin(), x[i].end());
        for (Node k : x[i]) {
            if (!k.f) {
                SegTree tmp = query(1, 1, MAXN, k.l, k.r);
                ans += (!tmp.mmin) * tmp.cnt;
                modify(1, 1, MAXN, k.l, k.r, 1);
            } else {
                modify(1, 1, MAXN, k.l, k.r, -1);
                SegTree tmp = query(1, 1, MAXN, k.l, k.r);
                ans += (!tmp.mmin) * tmp.cnt;
            }
        }
    }
    build(1, 1, MAXN);
    for (int i = 0; i <= MAXN; i++) {
        sort(y[i].begin(), y[i].end());
        for (Node k : y[i]) {
            if (!k.f) {
                SegTree tmp = query(1, 1, MAXN, k.l, k.r);
                ans += (!tmp.mmin) * tmp.cnt;
                modify(1, 1, MAXN, k.l, k.r, 1);
            } else {
                modify(1, 1, MAXN, k.l, k.r, -1);
                SegTree tmp = query(1, 1, MAXN, k.l, k.r);
                ans += (!tmp.mmin) * tmp.cnt;
            }
        }
    }
    cout << ans;
    return 0;
}

posted @ 2024-09-08 11:45 chengning0909 阅读(1) 评论(0) 编辑收藏举报

刷新页面返回顶部

Loading

cn 的小站

扫描线

扫描线

例题：洛谷 P5490

题意

思路

代码

洛谷 P7883

题意

思路

证明

代码

洛谷 P1502

题意

思路

代码

CF269D

题意

思路

代码

洛谷 P1856

题意

思路

代码

公告