李超线段树

合集 - 逐月总结(39)

1.ROIR 20242024-10-112.UER #72024-10-093.2024-10-8 #332024-10-084.BTS 242024-10-075.2024-10-7 #322024-10-076.2024-10-6 #312024-10-077.2024-10-4 #302024-10-078.2024-9-5 Div32024-10-049.2024-10-1 #282024-10-0210.2024-10-2 #292024-10-0211.DMOJ2024-10-0212.UER #12024-10-0213.CCPC Harbin2024-10-0114.TAP2024-09-3015.NAC2024-09-2916.2024-9-122024-09-2917.2024-9-132024-09-2918.CCO 2019 Day22024-09-2819.2024-9-272024-09-2820.EGOI2024-09-2721.湘潭夏令营2024-09-2622.2024-9-202024-09-2623.2024-9-24 #262024-09-2624.2024-9-252024-09-2525.异或线性基2024-09-20

26.李超线段树2024-09-06

27.JOI 2023 / 20242024-09-0428.OOI XVIII2024-10-1129.2024-10-9 #342024-10-1530.2024-10-10 #352024-10-1531.2024-10-14 #372024-10-1732.2024-10-15 #382024-10-1833.2024-10-11 #362024-10-2034.2024-10-17 #402024-10-2035.2024-10-21 逐月破星杯2024-10-2136.2024-10-16 NordicOI 20232024-10-2237.2024-10-22 逐月黯月杯2024-10-2238.2024-10-14 Div12024-10-2339.逐月新星杯2024-10-23

收起

李超线段树

李超线段树是线段树的一个变种，主要支持在平面直角坐标系中动态地插入线段或直线，并查询某一条平行于 $y$ 轴的直线与所有直线或线段的交点的纵坐标的最值。

---

假设只插入直线并且维护最大值：

在李超线段树中，对于每一个结点，我们需要维护的是在这个结点所对应的区间 $[l,r]$ 的中点处取值最大的直线。

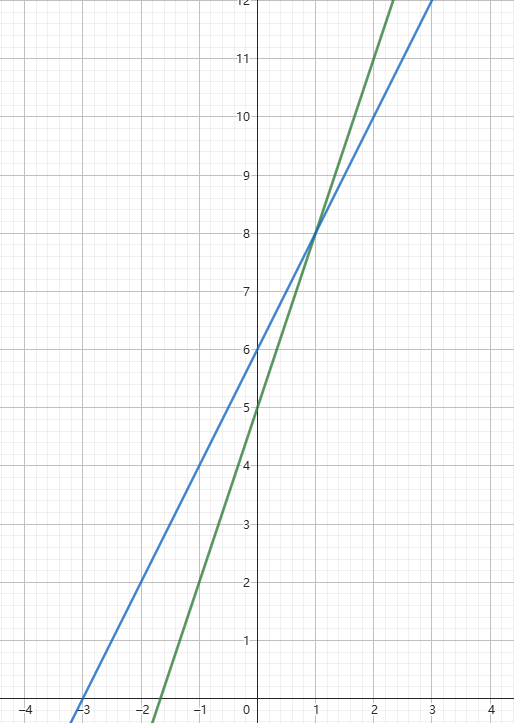
假设我们现在有两条直线 $y_1=3x+5,y_2=2x+6$，当前结点对应的区间为 $[1,4]$：

那么，我们就比较这两条直线在 $x=2$ 时的取值：

图中绿色直线是直线 $y=3x+5$，蓝色直线是 $y=2x+6$，很显然的，当 $x=2$ 时，直线 $y=3x+5$ 更优。

因此，区间 $[1,4]$ 所对应的直线就是 $y=3x+5$。

那么 $y=2x+6$ 应该怎么办呢？

这时，我们考虑比较这两条直线的斜率，我们会发现 $y=2x+6$ 的斜率更小一些，也就是意味着，当 $x>2$ 时，直线 $y=3x+5$ 的取值一定比 $y=2x+6$ 更大，因此，我们只会用这条直线更新左区间。

但是需要注意的是当两条直线斜率相同时，就可以直接退出了。

---

有时候为了防止一些小数的情况，李超线段树通常我会写成左闭右开的形式。

并且由于坐标的范围问题，通常我会写动态开点。

ll F(Node x, int pos) {
    return 1ll * x.k * pos + x.b;
}

void add(Node x) {
    int i = 1, l = -INF, r = INF + 1;
    while (l + 1 <= r) {
        if (tr[i].b == inf) {
            tr[i] = x; break;
        }

        int mid = l + (r - l) / 2;

        if (F(tr[i], mid) > F(x, mid)) swap(tr[i], x);
        if (l + 1 == r || tr[i].k == x.k) break;

        if (tr[i].k > x.k) {
            if (!son[i][1]) son[i][1] = ++c, tr[c] = {0, inf};
            i = son[i][1], l = mid;
        } else {
            if (!son[i][0]) son[i][0] = ++c, tr[c] = {0, inf};
            i = son[i][0], r = mid;
        }
    }
}

ll query(int x) {
    int i = 1, l = -INF, r = INF + 1;
    ll tp = inf;
    while (l + 1 <= r && i) {
        int mid = l + (r - l) / 2;

        tp = min(tp, F(tr[i], x));

        if (l + 1 == r) break;

        if (x < mid) i = son[i][0], r = mid;
        else i = son[i][1], l = mid;
    }
    return tp;
}

---

而如果是插入线段的话，事实上就是先找到线段所覆盖的区间，然后和直线一样更新线段树上的直线即可。

这里最需要注意的就是左闭右开区间的边界判断问题。

void modify(int i, int l, int r, int ql, int qr, Node x) {
    if (qr <= l || ql >= r) return ;
    if (ql <= l && r <= qr) {
        add(x, i, l, r);
        return ;
    }
    if (l + 1 == r) return ;
    int mid = l + (r - l) / 2;

    if (!son[i][0]) son[i][0] = ++c, tr[c] = {0, inf};
    modify(son[i][0], l, mid, ql, qr, x);

    if (!son[i][1]) son[i][1] = ++c, tr[c] = {0, inf};
    modify(son[i][1], mid, r, ql, qr, x);
}