可持久化 01 字典树
可持久化 01 字典树
01 字典树
回顾:字典树
将数字的 等长的二进制表示 作为字符串存储的字典树就是 01 字典树。
0 : 00
1 : 01
2 : 10
3 : 11
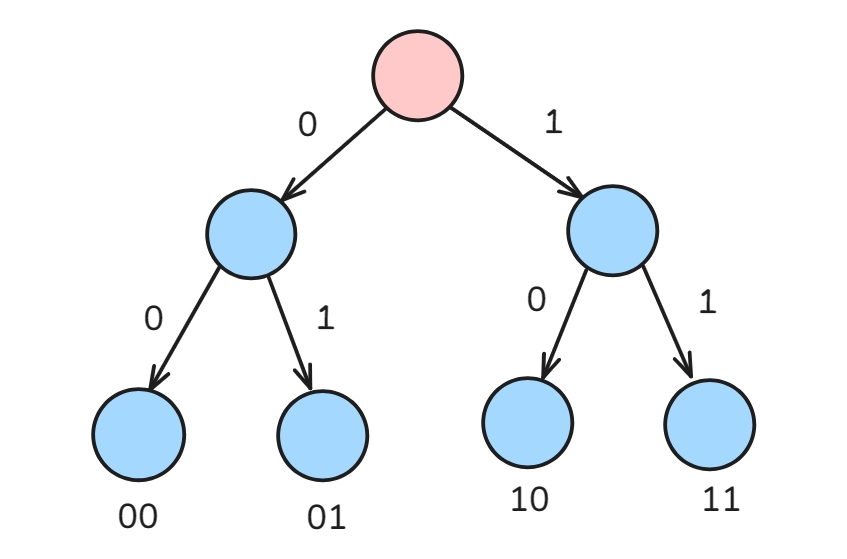
01 字典树所能解决的问题主要分为两种:
- 求出序列内的第 \(k\) 大 / 小
int query(int x) {
int ans = 0;
for (int u = 1, j = 29; j >= 0; j--) {
// 考虑左子树的元素数量是否超过 x,有点像线段树上二分
if (x > cnt[tr[u][0]]) x -= cnt[tr[u][0]], u = tr[u][1], ans += 1 << j;
else u = tr[u][0];
}
return ans;
}
- 求出 \(x\) 与序列中的某个数的异或和最大 / 最小值
这里有一个细节,那就是我们会尽量让高位选择不同的数字,所以从建树到查询都是得从最高位开始的。
void Insert(int x) {
for (int u = 1, j = 29; j >= 0; j--) {
int p = (x >> j) & 1;
if (!tr[u][p]) tr[u][p] = ++c;
u = tr[u][p], cnt[u]++;
}
}
void Erase(int x) {
for (int u = 1, j = 29; j >= 0; j--) {
int p = (x >> j) & 1;
u = tr[u][p], cnt[u]--;
}
}
int query(int x) {
int ans = 0;
for (int u = 1, j = 29; j >= 0; j--) {
int p = (x >> j) & 1;
// 对于每一位,如果是最大,尽量选择不同的数;如果是最小,尽量选择相同的数。
if (cnt[tr[u][p]]) u = tr[u][p];
else u = tr[u][!p], ans += 1 << j;
}
return ans;
}
可持久化 01 字典树与 01 字典树的唯一区别就是可以查询各个时刻的 01 字典树。
建树
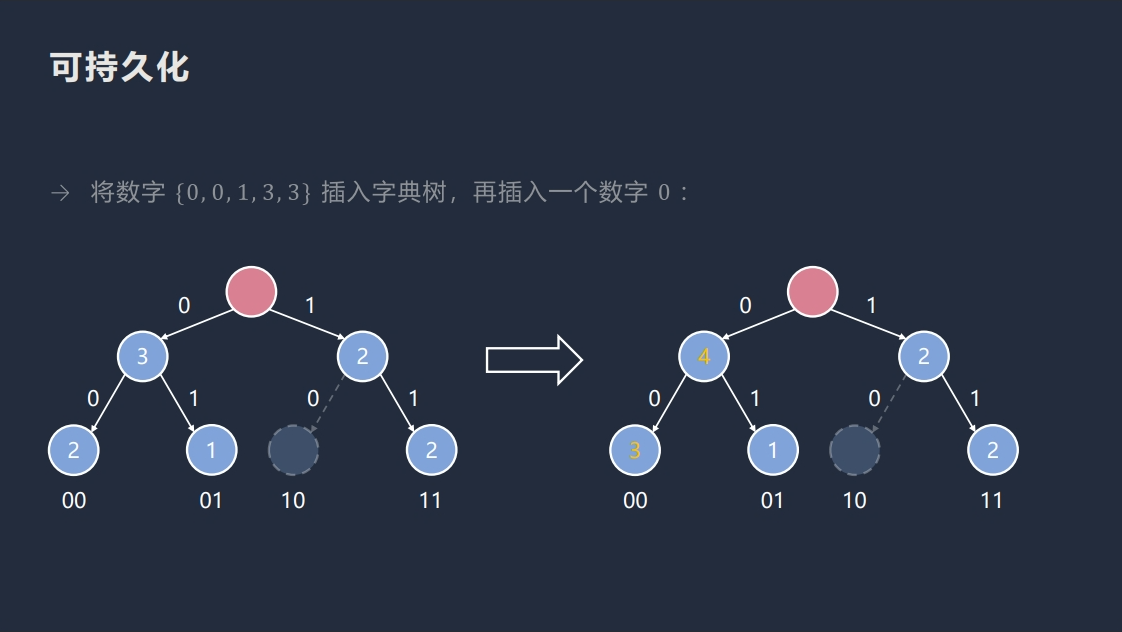
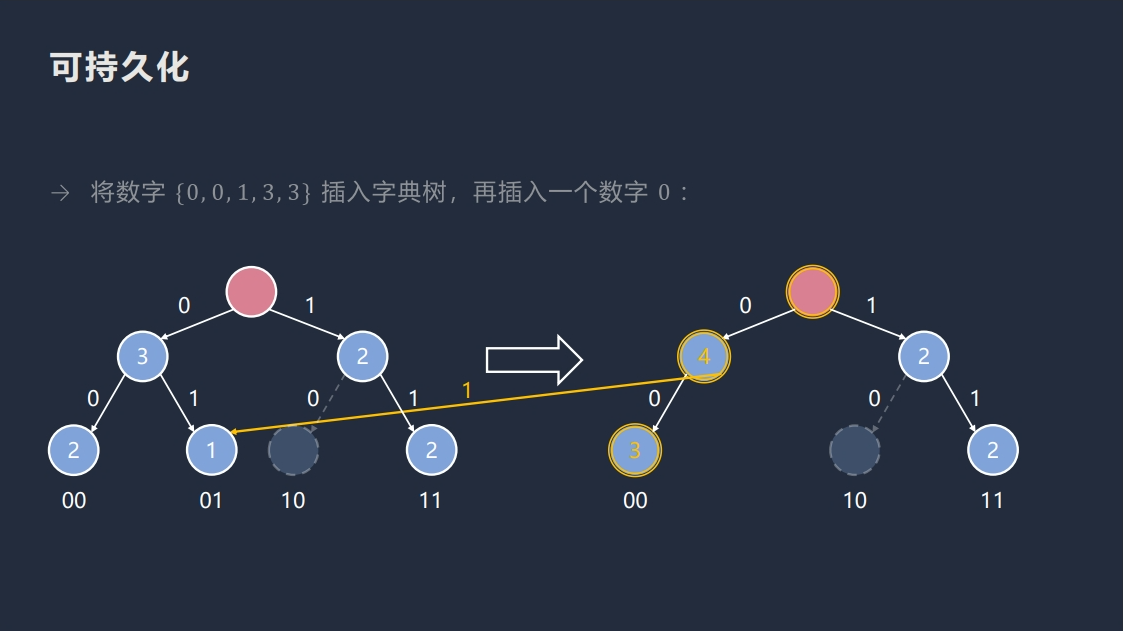
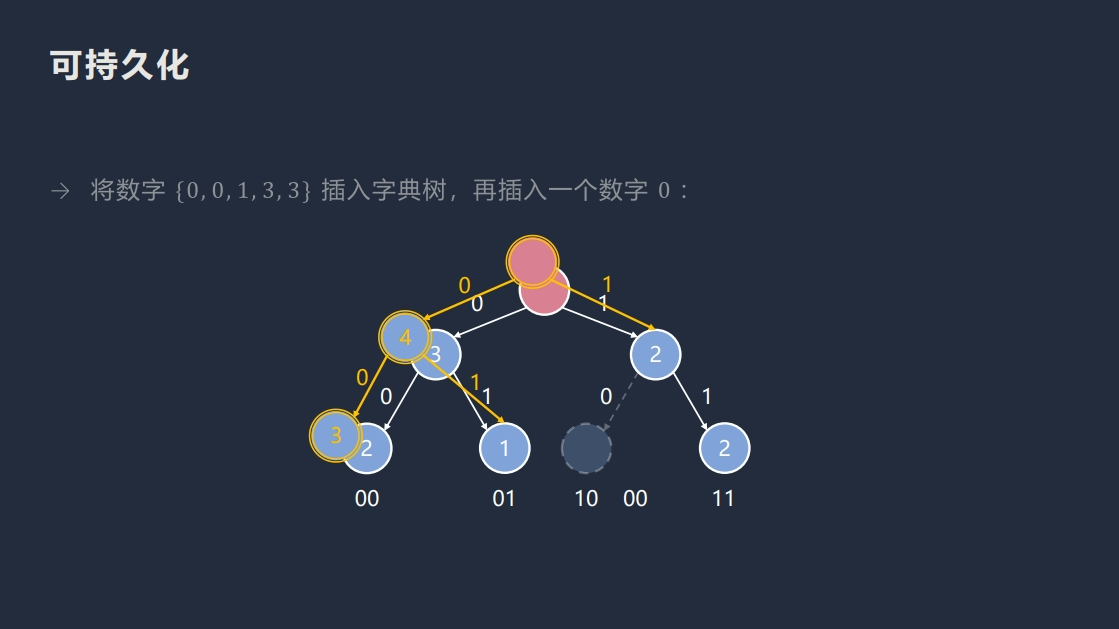
很显然的,我们不能在每次加入某个点的时候直接复制整棵树,空间会爆炸。
但是,我们可以发现,每次加入某个数 \(x\),都只会影响到 \(\log x\) 个结点,所以我们可以将不需要修改的部分直接连到某个历史版本上。
void modify(int prv, int x) {
root[++k] = ++c;
for (int u = root[k], j = 30; j >= 0; j--) {
int p = (x >> j) & 1;
tr[u][!p] = tr[prv][!p];
u = tr[u][p] = ++c, prv = tr[prv][p];
cnt[u] = cnt[prv] + 1;
}
}
查询区间第 \(k\) 小(大)
首先,我们考虑用 01 字典树查询的过程。
设点 \(x\) 的左儿子是 \(tr_{x, 0}\),右儿子是 \(tr_{x, 1}\),\(cnt_x\) 表示有多少个数在 \(x\) 的子树内。
对于当前所在点 \(pos\) 而言,每次先判断第 \(k\) 小是存在于左子树还是右子树,然后将这个问题变成在左子树查询第 \(k\) 小,或是在右子树查询第 \(k - cnt_{tr_{pos, 0}}\) 小。
我们再来考虑查询区间第 \(k\) 小的问题,同样的,我们每次要先判断第 \(k\) 小是在左子树还是右子树内(当前这一位是取 \(0\) 还是 \(1\)),但是,我们该怎么解决区间内有多少个数在某个结点的左子树内呢。
由于我们建树是直接建在某个历史版本的基础上,因此,我们可以使用类似于前缀和的方式解决。
也就是一个点从 \(l - 1\) 的根开始,另一个点从 \(r\) 的根开始,每次将两个点的 \(cnt\) 相减即可。
int query(int l, int r, int x) {
int ans = 0;
for (int u = root[l - 1], v = root[r], j = 30; j >= 0; j--) {
int k = cnt[tr[v][0]] - cnt[tr[u][0]];
if (x > k) x -= k, u = tr[u][1], v = tr[v][1], ans += 1 << j;
else u = tr[u][0], v = tr[v][0];
}
return ans;
}
查询区间异或和最大
还是一样,我们依旧先考虑用 01 字典树查询的过程。
对于当前点 \(pos\) 而言,假设 \(x\) 在当前这一位为 \(0\),那么我们肯定会希望当前这一位可以填数字 \(1\),也就是说,我们需要查询这一位填数字 \(1\) 是否可以,也就是是否存在这一位填 \(1\) 的数字,所以,我们还是像上一个问题一样用两个结点查询区间某种数的出现次数。
int query(int l, int r, int x) {
int ans = 0;
for (int u = root[l - 1], v = root[r], j = 30; j >= 0; j--) {
int p = (x >> j) & 1;
int k = cnt[tr[v][!p]] - cnt[tr[u][!p]];
if (k) u = tr[u][!p], v = tr[v][!p], ans += 1 << j;
else u = tr[u][p], v = tr[v][p];
}
return ans;
}
查询区间颜色数量
这是一个很有趣的问题,也可以用可持久化 01 字典树实现。
我们设颜色 \(x\) 上一次出现的位置为 \(last_x\),设 \(b_i = last_{a_i}\)。
如果我们是要查询区间内不同颜色的数量,也就是说,从 \(l\) 遍历到 \(r\),对于每一个 \(a_i\),如果它是在这个区间内第一次出现,它就会对答案有 \(1\) 的贡献。
转化一下就会变成:如果 \(a_i\) 在序列中上一次出现的位置不在区间 \([l, r]\) 内,它就会对答案有 \(1\) 的贡献。
所以,我们的问题就变成了查询区间内有多少个 \(b_i < l\)。
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n, m, tr[N * 21][2], cnt[N * 21], c = 1, k, root[N], s;
char op;
map<int, int> mp;
void modify(int prv, int x) {
root[++k] = ++c;
for (int u = root[k], j = 19; j >= 0; j--) {
int p = (x >> j) & 1;
tr[u][!p] = tr[prv][!p];
u = tr[u][p] = ++c, prv = tr[prv][p];
cnt[u] = cnt[prv] + 1;
}
}
int query(int l, int r) {
int ans = 0;
for (int u = root[l - 1], v = root[r], j = 19; j >= 0; j--) {
int p = (l >> j) & 1;
if (p) ans += cnt[tr[v][!p]] - cnt[tr[u][!p]];
u = tr[u][p], v = tr[v][p];
}
return ans;
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m, root[0] = 1;
for (int i = 1, x; i <= n; i++) cin >> x, modify(root[k], mp[x]), mp[x] = i;
while (m--) {
int a, b; cin >> a >> b;
cout << query(a, b) << '\n';
}
return 0;
}



