线段树
线段树
用来维护区间信息的数据结构,比如:区间最值,区间和等。
引入
首先,我们先思考这样一个问题:
给你一个长度为 \(n \ (1 \le n \le 10 ^ 5)\) 的序列 \(a\),有 \(m \ (1 \le m \le 10 ^ 5)\) 次询问,每次查询给定 \(l, r\),请你求出 \(l \sim r\) 的元素总和。
相信这个大家都会,用前缀和即可。
但是,如果有改变元素数值的操作呢?
如果我们将 \(a_p\) 改为 \(x\),那么在前缀和数组中,\(sum_p \sim sum_n\) 都会发生改变。
也就是说,在一个改变数值的操作中,我们最多会在前缀和数组上改变 \(n\) 个数值,那么,时间复杂度还是 \(O(n \times m)\),和暴力查找没有区别。
所以,这个时候,我们就需要用线段树来维护这些信息了。
基本结构
线段树本质上就是一棵树,每个结点代表一段区间。
假设我们现在有一个数组 \(a = \{10, 11, 12, 13, 14\}\),要维护区间和,那么,线段树就应该像这样:

也就是说,我们每次将一个大区间分成两段,再由两段小区间合并成这个大区间。
并且,二叉树本身有一种表示方法:结点 \(i\) 的两个儿子分别是 \(2 \times i, 2 \times i + 1\)。
所以我们可以靠这个来快速合并与查询儿子区间。
那么我们还是考虑上面那个问题,下面给出建树的代码:
int Make_tree(int i, int l, int r) {
if (l == r) {
return tr[i] = a[l];
}
int mid = (l + r) >> 1;
return tr[i] = Make_tree(i * 2, l, mid) + Make_tree(i * 2 + 1, mid + 1, r);
}
时间复杂度为 \(O(n)\)。
修改某个元素
由于我们修改的是某个指定结点的值,所以,我们可以发现,在每次递归的时候,肯定只有一个区间中包含这个下标,就不用递归两个区间了。
注意:在你修改完值之后退出时,记得一定要修改线段树中的元素!!!把它变成修改之后的和
代码大概就是这样的:
void modify(int i, int l, int r, int p, int x) {
if (l == r) {
tr[i] = x;
return ;
}
int mid = (l + r) >> 1;
p <= mid ? modify(i * 2, l, mid, p, x) : modify(i * 2 + 1, mid + 1, r, p, x);
tr[i] = tr[i * 2] + tr[i * 2 + 1];
}
时间复杂度为 \(O(\log n)\)。
求区间信息
本身,我们维护这个线段树就是为了求出区间信息,所以,我们应该怎么快速地求出这些信息呢?
假设我们要求出区间 \([ql, qr]\) 的元素之和,对于我们当前递归到的这个区间 \([l, r]\),分三种情况:
-
如果 \([l, r]\) 被 \([ql, qr]\) 完全包含,就可以直接加上这个区间的和,停止递归。
-
如果 \([l, r]\) 和 \([ql, qr]\) 完全没有交集,就直接退出。
-
否则,继续递归。
int Sum(int i, int l, int r, int ql, int qr) {
if (qr < l || ql > r) return 0;
// qr < l : ql ..... qr .... l .... r 查询区间在当前递归的区间的左边,没有交集
// ql > r : l ..... r .... ql .... qr 查询区间在当前递归的区间的右边,没有交集
if (ql <= l && r <= qr) return tr[i]; // 当前递归的区间被查询区间完全包含
int mid = (l + r) >> 1;
return Sum(i * 2, l, mid, ql, qr) + Sum(i * 2 + 1, mid + 1, rl, ql, qr);
}
区间修改和懒标记
如果,我们要改变的不是一个元素,而是很多元素呢?
譬如说,我们需要给 \([ql, qr]\) 的所有元素加上 \(k\),如果暴力枚举所有点做单点修改,还不如直接暴力修改元素的值,所以,我们需要快速的修改它们。
还是考虑当前递归的区间 \([l, r]\),就像我们刚才求区间信息一样,分三种情况讨论。
-
如果 \([l, r]\) 和 \([ql, qr]\) 没有交集,那么这次修改不会影响到这个区间,直接退出。
-
如果 \([l, r]\) 被 \([ql, qr]\) 完全包含,那么直接更改 \([l, r]\) 的和,并且将 \(k\) 打在懒标记上,停止递归。
-
否则,继续递归。
那么,这个懒标记到底是什么呢?
其实,因为我们是直接更改区间和,所以,\([l, r]\) 的子区间是没有进行改变的,那么,如果后面的查询操作查询到了 \([l, r]\) 的子区间,会对答案有影响,所以,我们需要一个懒标记来记录 \([l, r]\) 这一段还有多少值没有加给 \([l, r]\) 的子区间。
那么,我们在查询区间信息时,就需将每个区间的懒标记对应的值加到它的子区间上,我们称这个操作为懒标记下传。
注意:
-
懒标记所记录的是子区间需要加上的数值,并不需要加给区间本身。
-
懒标记是需要传给子区间的,也就是说,子区间的懒标记需要加上当前区间的懒标记,因为还要传给子区间的子区间(儿子的儿子)。
void update(int i, int l, int r, int k) {
lazy[i] += k, tr[i] += (r - l + 1) * k;
}
void pushdown(int i, int l, int mid, int r) { // 懒标记下传
update(i * 2, l, mid, lazy[i]), update(i * 2 + 1, mid + 1, r, lazy[i]), lazy[i] = 0;
}
void modify(int i, int l, int r, int ql, int qr, int k) {
if (qr < l || ql > r) return ;
if (ql <= l && r <= qr) {
tr[i] += (r - l + 1) * k, lazy[i] += k;
return ;
}
int mid = (l + r) >> 1;
pushdown(i, l, mid, r);
modify(i * 2, l, mid, ql, qr, k), modify(i * 2 + 1, mid + 1, r, ql, qr, k);
tr[i] = tr[i * 2] + tr[i * 2 + 1];
}
永久化标记
这大概是懒标记的一个不完全版本,可以维护的问题是比较有限的。
首先,我们先说一下什么是永久化标记。
假设,我们有两种操作,第一种是区间 \([l, r]\) 加上 \(x\),第二种是查询区间和。
假设原数组 \(a = \{1, 2, 3, 4, 5\}\),我们已经对 \([1, 4]\) 加上了 \(5\),那么,如果用懒标记实现,应该是这样的:

然后,我们下传标记:

但是如果我们使用的是永久化标记,就是这样的:

这样打标记的话,当我们查询的时候,只需要在从下往上回溯时加上对应的数值即可,相比于懒标记,减少了下传的过程,可以降低常数,并且似乎在一些撤销操作上有独特的优势。
但是永久化标记也有一些限制,如果我们交换操作顺序会改变结果的话,永久化标记大概率是无法维护的,这时,就还是得使用懒标记。
看一个例题:
abc342 G
题意
有一个长度为 \(n\) 的整数序列 \(a\),有 \(q\) 次操作,操作分为三种类型:
- 由三个整数 \((l, r, x)\) 表示,用 \(max(a_i, x)\) 替换 \(a_i \ (l \le i \le r)\)。
- 由一个整数 \(i\) 表示,撤销第 \(i\) 次操作,保证第 \(i\) 次操作是 1 操作并且尚未取消。
- 由一个整数 \(i\) 表示,输出当前的 \(a_i\)。
思路
我们考虑使用永久化标记,也就是说,对于区间 \([l, r]\) 所对应的每一个区间,都用 \(x\) 更新标记。
但是,由于我们需要撤销操作,又需要维护标记中的最大值,所以我们可以用 set 维护标记,在撤销时 erase 掉标记,修改时 insert 标记。
这种撤销的操作用永久化标记维护会更加方便,因为如果使用懒标记,通常在撤销时,这次操作的影响已经下传了,也就是说,我们需要多对很多结点进行撤销操作,就无法保证时间复杂度了。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
struct Node {
int l, r, x;
} que[N];
int n, a[N], op, q;
multiset<int> tr[4 * N];
void build(int i, int l, int r) {
if (l == r) {
tr[i].insert(a[l]); return ;
}
int mid = (l + r) >> 1;
build(i * 2, l, mid), build(i * 2 + 1, mid + 1, r);
}
void modify(int i, int l, int r, int ql, int qr, int x, int k) {
if (qr < l || ql > r) return ;
if (ql <= l && r <= qr) {
if (!k) tr[i].insert(x);
else tr[i].erase(tr[i].find(x));
return ;
}
int mid = (l + r) >> 1;
modify(i * 2, l, mid, ql, qr, x, k), modify(i * 2 + 1, mid + 1, r, ql, qr, x, k);
}
int query(int i, int l, int r, int p) {
if (l == r) return *tr[i].rbegin();
int mid = (l + r) >> 1;
int k = (p <= mid ? query(i * 2, l, mid, p) : query(i * 2 + 1, mid + 1, r, p));
return tr[i].empty() ? k : max(k, *tr[i].rbegin());
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
build(1, 1, n);
cin >> q;
for (int i = 1; i <= q; i++) {
cin >> op;
if (op == 1) {
int l, r, x; cin >> l >> r >> x;
que[i] = {l, r, x};
modify(1, 1, n, l, r, x, 0);
} else if (op == 2) {
int x; cin >> x;
modify(1, 1, n, que[x].l, que[x].r, que[x].x, 1);
} else {
int x; cin >> x;
cout << query(1, 1, n, x) << '\n';
}
}
return 0;
}
线段树优化建图
先看一个例题
CF786B
题意
有一个 \(n\) 个点的有向图,有 \(q\) 个操作,操作分为三种:
- 有一条从 \(u\) 到 \(v\)的边, 边权为 \(w\)。
- \(u\) 到区间 \([l, r]\) 的每个点都有一条边,边权为 \(w\)。
- 区间 \([l, r]\) 的每个点都有一条到 \(u\) 的边,边权为 \(w\)。
请在 \(q\) 次操作结束后,求出从 \(1\) 到 \(i \ (1 \le i \le n)\) 的最小距离。
思路
首先,我们可以想到暴力的对于每个 2, 3 操作连边,但是显然,这样时间复杂度是 \(O(q \times n)\) 的,不够优秀。
由于我们是对区间连边,所以可以考虑用线段树优化建图。

很显然的,图中每一条绿色的边的边权都应该是 \(0\),但是,如果我们真的像这样直接连每条绿色的双向边,最终答案就会全为 \(0\),所以,我们可以考虑用两颗线段树连边,一颗线段树维护从儿子到父亲的边,另一颗线段树维护从父亲到儿子的边:
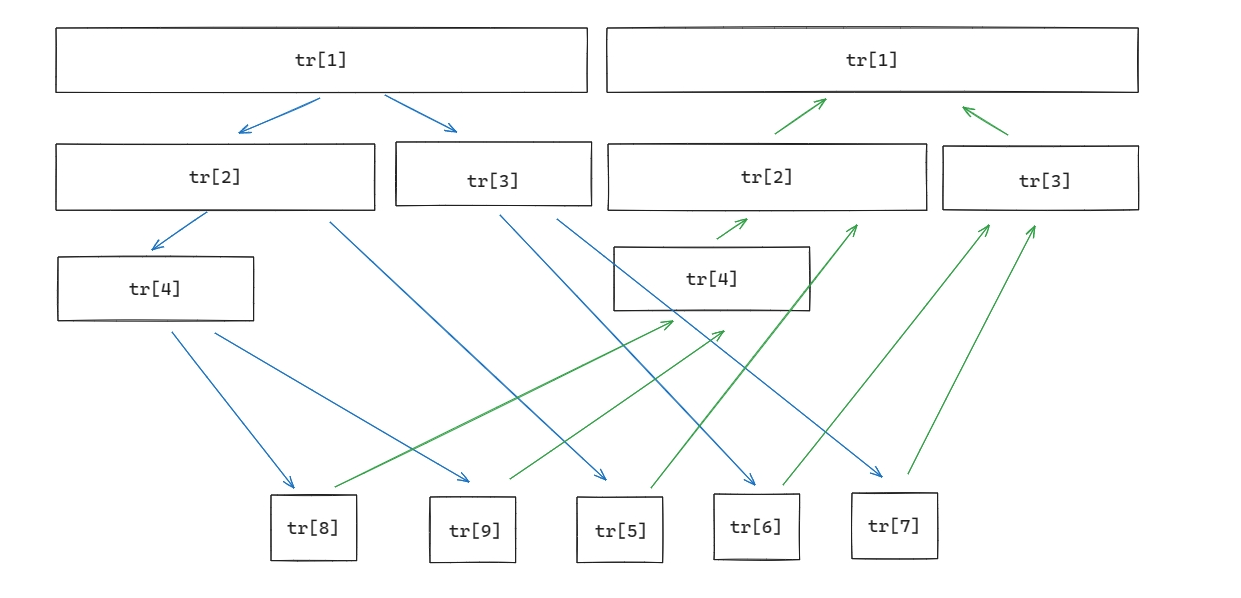
当然,我们要让两颗线段树的编号不同,所以,我们可以这样编号:

void build(int i, int l, int r, int k) {
if (l == r) {
f[i] = h[i] = l;
return ;
}
int mid = (l + r) >> 1;
if (!k) f[i] = ++cnt;
else h[i] = ++cnt;
build(i * 2, l, mid, k), build(i * 2 + 1, mid + 1, r, k);
if (!k) g[f[i]].push_back({f[i * 2], 0}), g[f[i]].push_back({f[i * 2 + 1], 0}); // 从父亲到儿子
else g[h[i * 2]].push_back({h[i], 0}), g[h[i * 2 + 1]].push_back({h[i], 0}); // 从儿子到父亲
}
然后,我们就可以用类似线段树查询的方式对区间建边了。
void Add_Edge(int i, int l, int r, int ql, int qr, int x, int k, int w) {
if (qr < l || ql > r) return ;
if (ql <= l && r <= qr) {
if (!k) g[x].push_back({f[i], w});
else g[h[i]].push_back({x, w});
return ;
}
int mid = (l + r) >> 1;
Add_Edge(i * 2, l, mid, ql, qr, x, k, w), Add_Edge(i * 2 + 1, mid + 1, r, ql, qr, x, k, w);
}
然后就可以正常的跑一遍 \(Dijkstra\) 了,但是,在这里有一个特别需要注意的点,就是每个数组的大小,譬如说,你建好两颗线段树后总结点数量会达到 \(8 \times n\) 的级别。
代码
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5 + 10;
struct Node {
int v;
ll w;
bool operator < (const Node &i) const {
return w > i.w;
}
};
int n, q, s, cnt, f[4 * N], h[4 * N]; // f : down h : up
ll d[8 * N];
vector<Node> g[8 * N];
priority_queue<Node> pq;
void build(int i, int l, int r, int k) {
if (l == r) {
f[i] = h[i] = l;
return ;
}
int mid = (l + r) >> 1;
if (!k) f[i] = ++cnt;
else h[i] = ++cnt;
build(i * 2, l, mid, k), build(i * 2 + 1, mid + 1, r, k);
if (!k) g[f[i]].push_back({f[i * 2], 0}), g[f[i]].push_back({f[i * 2 + 1], 0});
else g[h[i * 2]].push_back({h[i], 0}), g[h[i * 2 + 1]].push_back({h[i], 0});
}
void Add_Edge(int i, int l, int r, int ql, int qr, int x, int k, int w) {
if (qr < l || ql > r) return ;
if (ql <= l && r <= qr) {
if (!k) g[x].push_back({f[i], w});
else g[h[i]].push_back({x, w});
return ;
}
int mid = (l + r) >> 1;
Add_Edge(i * 2, l, mid, ql, qr, x, k, w), Add_Edge(i * 2 + 1, mid + 1, r, ql, qr, x, k, w);
}
void Dijkstra() {
fill(d + 1, d + 8 * n + 1, 1e18);
d[s] = 0, pq.push({s, 0});
while (!pq.empty()) {
Node u = pq.top(); pq.pop();
if (u.w != d[u.v]) continue;
for (Node v : g[u.v]) {
if (d[v.v] > u.w + v.w) {
d[v.v] = u.w + v.w;
pq.push({v.v, d[v.v]});
}
}
}
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> q >> s, cnt = n;
build(1, 1, n, 0), build(1, 1, n, 1);
for (int i = 1; i <= q; i++) {
int op; cin >> op;
if (op == 1) {
int u, v, w; cin >> u >> v >> w;
g[u].push_back({v, w});
} else {
int u, l, r, w; cin >> u >> l >> r >> w;
Add_Edge(1, 1, n, l, r, u, op - 2, w);
}
}
Dijkstra();
for (int i = 1; i <= n; i++) {
cout << (d[i] == 1e18 ? -1ll : d[i]) << ' ';
}
return 0;
}
所以,总结一下,线段树优化建图主要就是用在对区间建边的情况上,有时候可能要建一些中间点,也就是对多个点到多个点建边时,可以用中间点向两个点集中的所有点分别建边,就像是 洛谷 P1983 所用的建图优化一样。



