abc 248 F 题解
abc 248 F
题意
给定一个大于等于 \(2\) 的整数 \(N\) 和一个质数 \(P\), 现在有一个有 \(2N\) 个点,\(3N - 2\) 条边的图 \(G\)。
令点的编号分别为 \(1, 2, \dots, 2N\),令边的编号为 \(1, 2, \dots, 3N - 2\),则按照以下方式建边得到图 \(G\):
-
对于 \(1 \le i \le N - 1\),边 \(i\) 连接点 \(i\) 和 \(i + 1\)。
-
对于 \(1 \le i \le N - 1\),边 \(N + i - 1\) 连接点 \(N + i\) 和 \(N + i + 1\)。
-
对于 \(1 \le i \le N\),边 \(2N + i - 2\) 连接点 \(i\) 和 \(N + i\)。
对于 \(i = 1, 2, \dots, N - 1\),请你求出有多少种删 \(i\) 条边的方案,使得图 \(G\) 仍然是联通的,方案数对 \(P\) 取模。
\(2 \le N \le 3000\)
\(9 \times 10 ^ 8 \le P \le 10 ^ 9\)
Sample 1
Input
3 998244353
Output
7 15
Sample 2
Input
16 999999937
Output
46 1016 14288 143044 1079816 6349672 29622112 110569766 330377828 784245480 453609503 38603306 44981526 314279703 408855776
思路
首先,我们先将 Sample 1 的图 \(G\) 建立出来。
也就是长这样的:
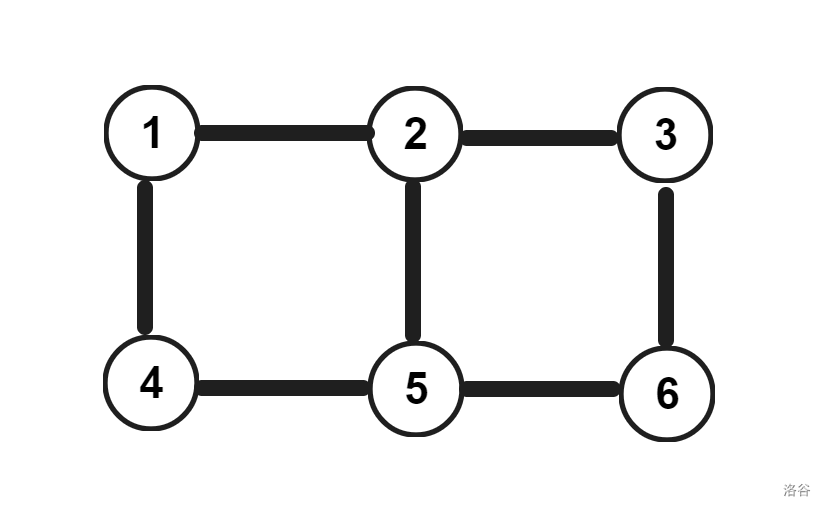
我们可以发现,这就是由很多个正方形拼成的图,每一列的两个点就是 \(i\) 和 \(i + N\)。
那么,我们先考虑一个问题,如果我们不要求删去 \(i\) 条边,而是只要满足删边使得图连通,应该怎么做呢?
我们将每一列看作成一个整体,所以对于前 \(i\) 列来说,没有连通的肯定是它的一段后缀,因为只有一段后缀是有可能通过后来加边而连通的。
所以,\(dp_{i, 0 / 1}\) 表示前 \(i\) 列是否连通的删边方案数。
那么,我们考虑转移:
如果前 \(i\) 列连通,那么:
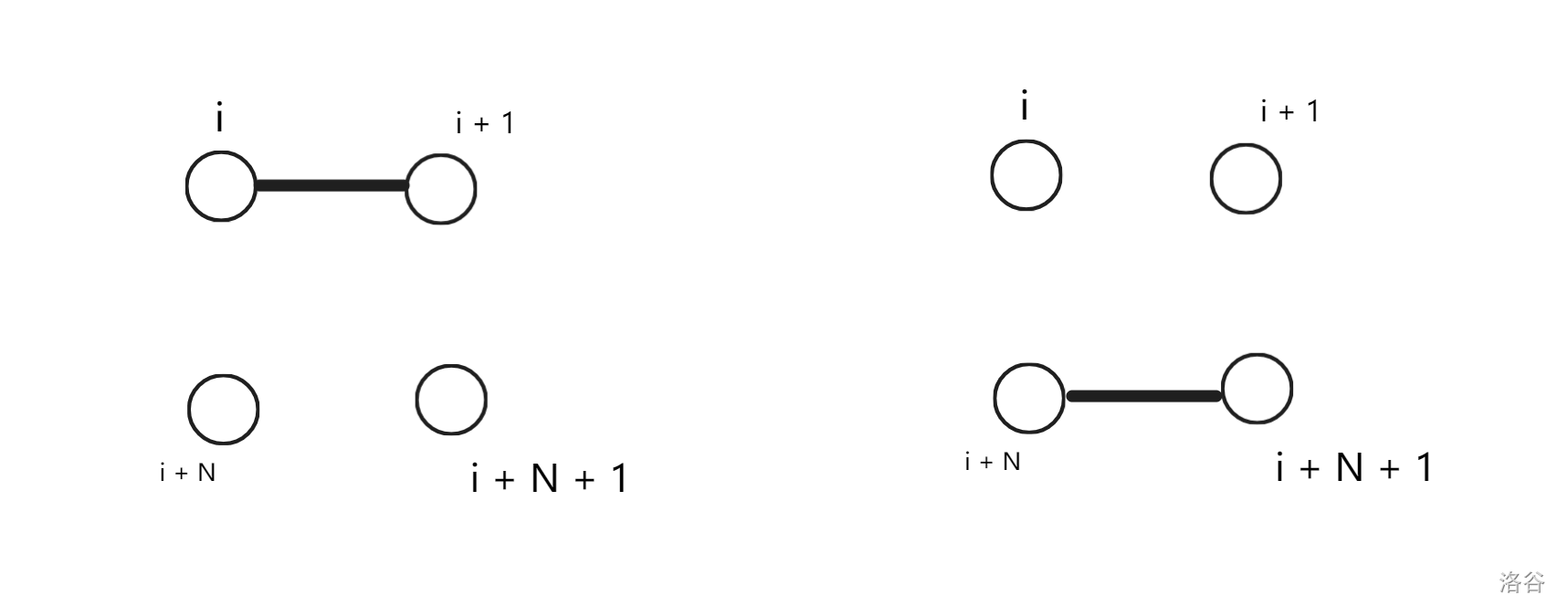
可以看出,这两种转移会使得第 \(i + 1\) 列不连通,也就是从 \(dp_{i, 1}\) 转移到 \(dp_{i + 1, 0}\)。
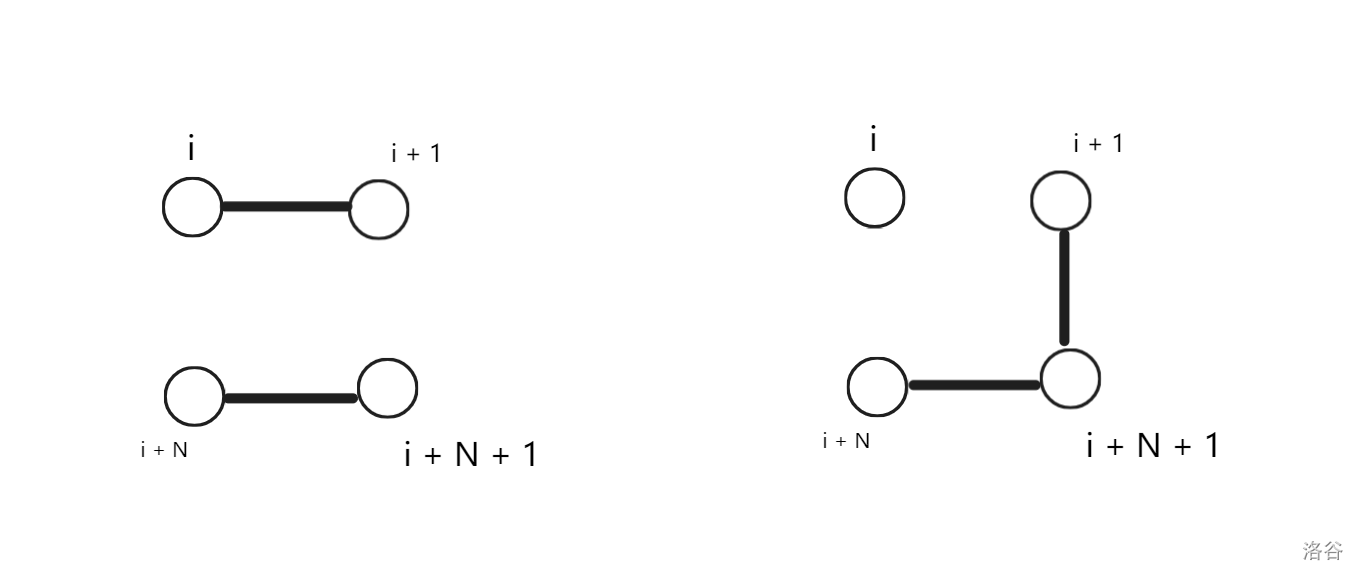
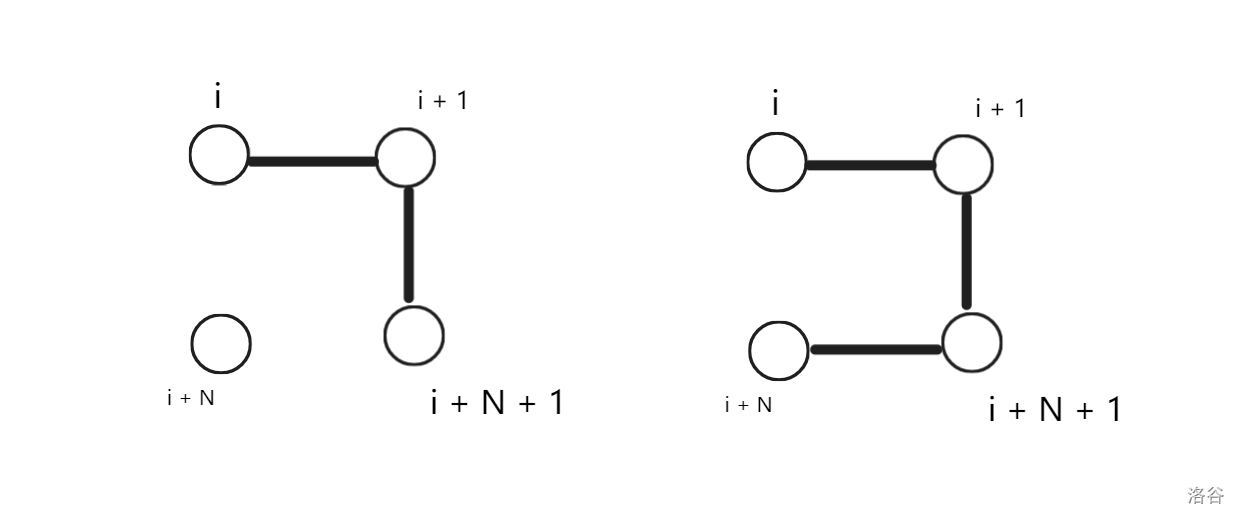
而这四种转移会使得第 \(i + 1\) 列连通,也就是从 \(dp_{i, 1}\) 转移到 \(dp_{i + 1, 1}\)。
我们再考虑第 \(i\) 列不连通:
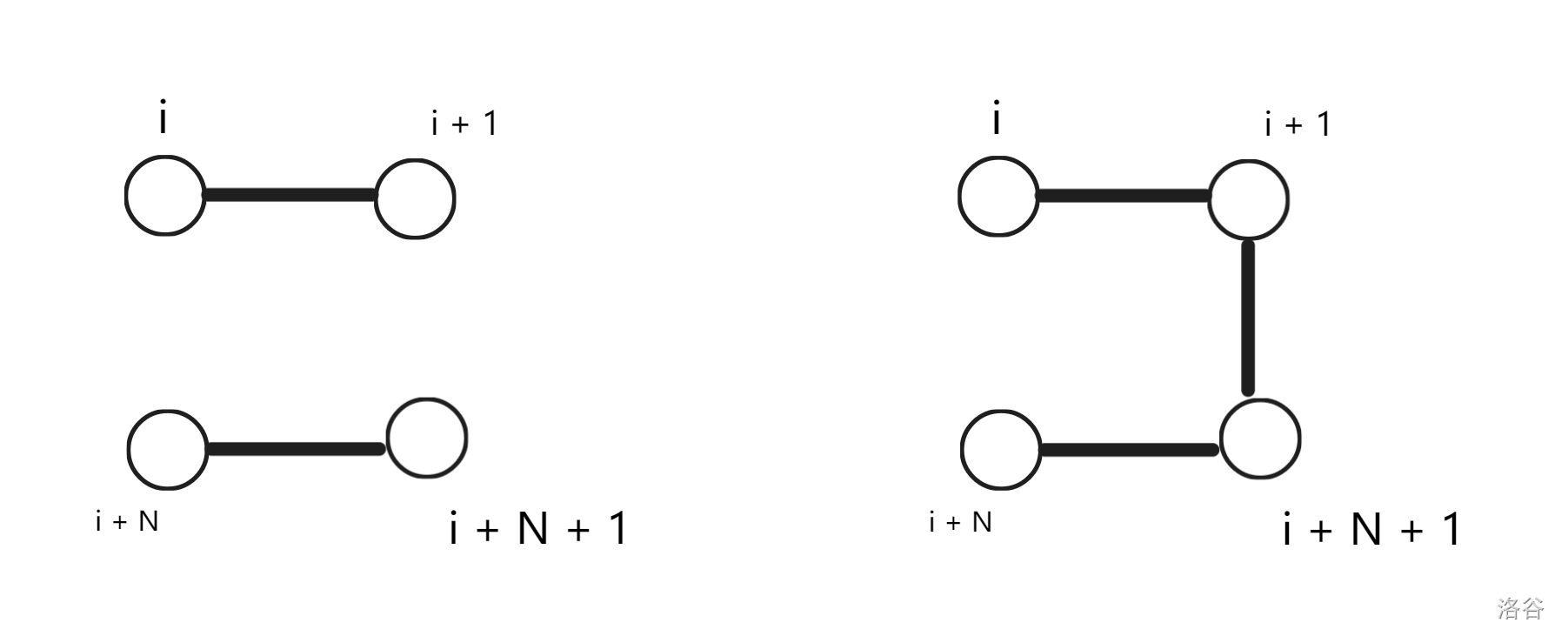
这两种转移分别会使得第 \(i + 1\) 列不连通和联通,也就是从 \(dp_{i, 0}\) 分别转移到 \(dp_{i + 1, 0}\) 和 \(dp_{i + 1, 1}\)。
那么,要求了删去的边的数量也是一样的。
\(dp_{i, j, 0 / 1}\) 表示前 \(i\) 列删去 \(j\) 条边是否连通的方案数。
那么转移就是:
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 3010;
int n, p;
long long dp[N][N][2];
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> p;
dp[1][0][1] = dp[1][1][0] = 1; // 初始状态
for (int i = 1; i <= n; i++) {
for (int j = 0; j < n; j++) {
dp[i + 1][j + 2][0] = (dp[i + 1][j + 2][0] + 2 * dp[i][j][1]) % p;
dp[i + 1][j + 1][1] = (dp[i + 1][j + 1][1] + 3 * dp[i][j][1]) % p;
dp[i + 1][j][1] = (dp[i + 1][j][1] + dp[i][j][1]) % p;
dp[i + 1][j + 1][0] = (dp[i + 1][j + 1][0] + dp[i][j][0]) % p;
dp[i + 1][j][1] = (dp[i + 1][j][1] + dp[i][j][0]) % p;
}
}
for (int i = 1; i < n; i++) {
cout << dp[n][i][1] << ' ';
}
return 0;
}



