USACO22OPEN 题解
T1 Visits S
题意
Bessie 的 \(N\)(\(2\le N\le 10^5\))个奶牛伙伴(编号为 \(1\cdots N\))每一个都拥有自己的农场。对于每个 \(1\le i\le N\),伙伴 i 想要访问伙伴 \(a_i\)(\(a_i\neq i\))。
给定 \(1\ldots N\) 的一个排列 \((p_1,p_2,\ldots, p_N)\),访问按以下方式发生。
对于 \(1\) 到 \(N\) 的每一个 \(i\):
- 如果伙伴 \(a_{p_i}\) 已经离开了她的农场,则伙伴 \(p_i\) 仍然留在她的农场。
- 否则,伙伴 \(p_i\) 离开她的农场去访问伙伴 \(a_{p_i}\) 的农场。这次访问会产生快乐的哞叫 \(v_{p_i}\) 次(\(0\le v_{p_i}\le 10^9\))。
对于所有可能的排列 \(p\),计算所有访问结束后可能得到的最大哞叫次数。
思路
做法一
我们将所有的拜访关系都看做成是一条有向边,从 \(i\) 连向 \(a_i\)。
由于这道题目的所有点的出度都为 \(1\),所以很明显,这道题目的图最终建出来会是一个 基环内向森林。
差不多就长这样:
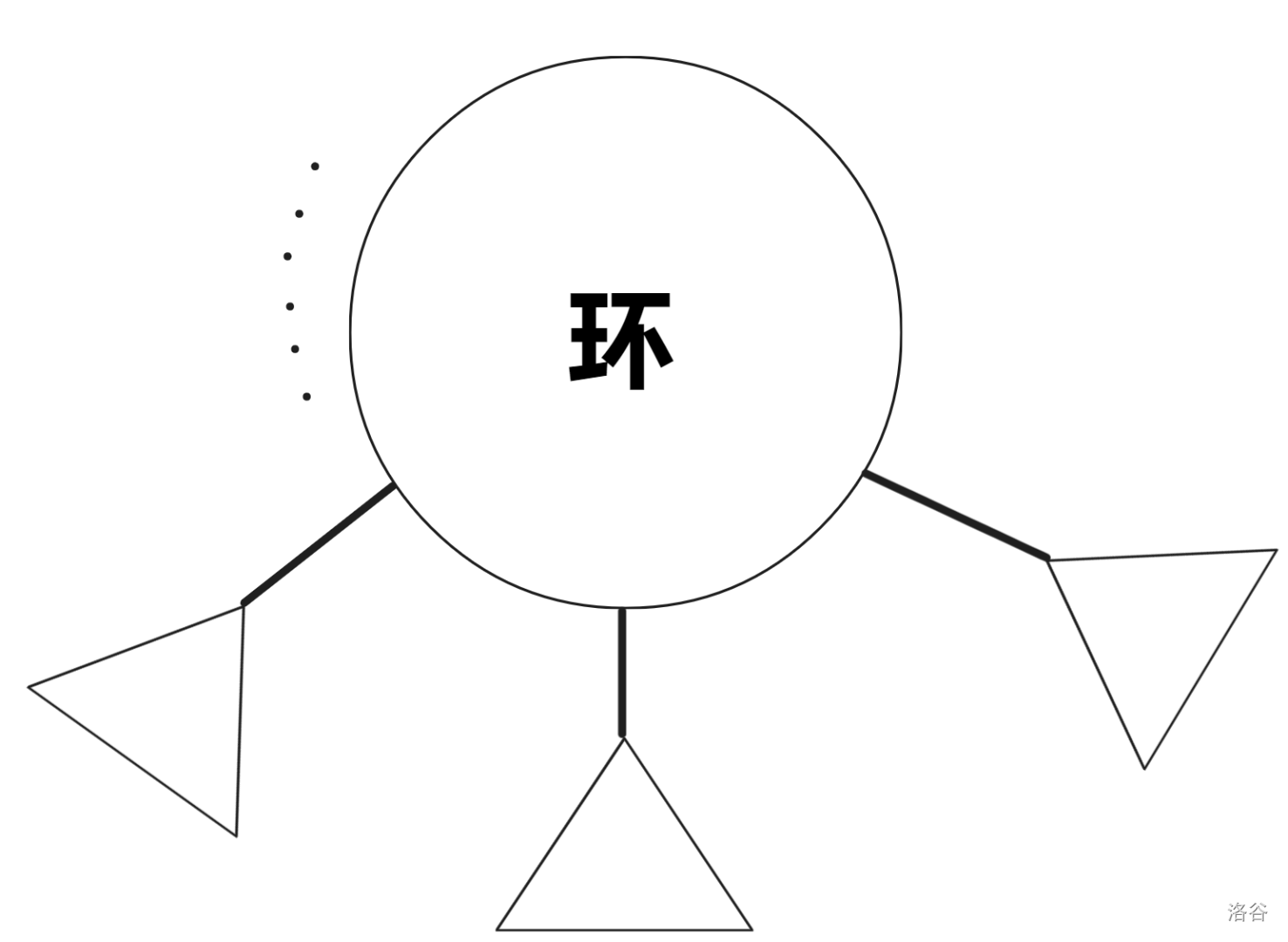
所以我们先处理这个森林中的每一棵树除去环的部分,也就是从入度为 \(0\) 的点开始向环搜索。
再去处理所有树上的环,也就是将环上的所有点权的最小值丢掉。
最后将所有树的答案累加即可。
时间复杂度为 \(O(n)\)。
做法二
可以想到,既然要让所有点权的和最大,那么可以直接联想到最大生成树。
既然是最大生成树,那么我们就可以将点 \(i\) 的点权看作为点 \(i\) 到点 \(a_i\) 这一条边的边权。
所以做法就很简单了:
-
将所有的点权转换成边权,按照权值排序。
-
枚举每一条边,用并查集维护两点是否在同一连通块内,若不在,将两个连通块合并,并将边权累加,否则,直接跳到下一条边。
时间复杂度为 \(O(n \times \log n)\)。
T2 Subset Equality S
题意
奶牛们正在尝试一种相互交换编码信息的新方法,她们在相关的字母中混入不相关的字母,使信息难以解码。
奶牛们传输两个字符串 \(s\) 和 \(t\),每个字符串的长度不超过 \(10^5\),仅由小写字母 'a' 到 'r' 组成。为了尝试理解这条编码消息,你将被给定 \(Q\) 个询问(\(1 \leq Q \leq 10^5\))。
每个询问给定小写字母 'a' 到 'r' 的一个子集。你需要对每个询问判断 \(s\) 和 \(t\) 在仅包含询问中给定的字母时是否相等。
思路
设题目给定的字符集为 \(S\),那么只保留 \(S\) 中的字符时,两个字符串分别变为 \(s', t'\)。
那么,如何判断 \(s'\) 和 \(t'\) 是否相等呢?
最暴力的方法就是从左到右枚举每一个字符,判断是否相等。
那么,我们假设 \(s'\) 不等于 \(t'\),则说明肯定存在一个最小的 \(1 \le i \le \min(|s'|, |t'|)\),且 \(s'_i \ne t'_i\),也就是说,\(i\) 是第一个满足 \(s'_i \ne t'_i\) 的下标。
所以,\(s'_1, s'_2, \dots s'_{i - 1} = t'_1, t'_2, \dots t'_{i - 1}\),那么这就意味着,我们可以将 \(S\) 缩成 \(\{s'_i, t'_i\}\),因此,要判断字符集 \(S\) 是否会让 \(s, t\) 不同,本质上就是判断 \(S\) 中 是否存在大小为 \(1\) 或 \(2\) 的子集使得 \(s, t\) 不同。
具体做法就是:
-
先预处理出所有大小为 \(1\) 或 \(2\) 的子集是否会让 \(s, t\) 不同。
-
每次询问枚举 \(S\) 中的所有大小为 \(1\) 或 \(2\) 的子集,判断是否存在子集使得 \(s, t\) 不同。
T3 COW Operations S
题意
Bessie 找到了一个长度不超过 \(2 \cdot 10^5\) 且仅包含字符 'C','O' 和 'W' 的字符串 \(s\)。她想知道是否可以使用以下操作将该字符串变为单个字母 'C'(她最喜欢的字母):
-
选择两个相邻相等的字母并将其删除。
-
选择一个字母,将其替换为另外两个字母的任一排列。
求出这个字符串本身的答案对 Bessie 而言并不足够,所以她想要知道 \(s\) 的 \(Q\)(\(1\le Q\le 2\cdot 10^5\))个子串的答案。
思路
首先,我们先枚举一下。
| 长度 | 原串 | 操作后的串 |
|---|---|---|
| 1 | C | OW, WO |
| 1 | O | CW, WC |
| 1 | W | CO, OW |
| 2 | CC | \(\emptyset\) |
| 2 | CO | W |
| 2 | CW | O |
| 2 | OC | W |
| 2 | OO | \(\emptyset\) |
| 2 | OW | C |
| 2 | WC | O |
| 2 | WO | C |
| 2 | WW | \(\emptyset\) |
可以发现几个特殊性质:
-
相邻两个不同字母可以通过操作变成第三个字母,这意味着变换操作是可逆的,而且任意相邻两个字母都可以进行操作。
-
相邻字母的操作满足交换律和结合律。
而这里,我们就不得不提到一些关于单位元和逆元的知识了:
单位元
单位元:在一个集合中,对于某种运算,如果对于任意集合的元素 \(a\),与元素 \(e\) 进行运算,得到的答案是元素 \(a\) 本身,那么元素 \(e\) 为当前运算下的单位元。
比如说,在加法中,单位元为 \(0\)。在乘法中,单位元为 \(1\)。
逆元
逆元:在一个集合中,对于某种运算,如果任意两个元素的运算结果等于单位元,则称这两个元素互为逆元。
比如说,在加法运算中,任意实数 \(a\) 的逆元为 \(-a\)。
我们再看到前缀和,前缀和实际上是需要满足三个条件的:
-
运算具有交换律。
-
运算具有结合律。
-
运算有逆元和单位元。
所以,我们可以将这个操作看做成是一种运算,那么在这种运算中, \(a\) 的逆元就是 \(a\)。
所以做法就是:
-
预处理出前缀和(\(s_1, s_2 \dots s_n\))。
-
对于每次询问,将 \(s_r\) 与 \(s_{l - 1}\) 做运算,判断是否等于
C。
但是,其实这题还有更简便的方法。
我们可以将这种运算看做成是异或,而 \(\emptyset\) 为 \(0\),C 为 \(1\),O 为 \(2\),W 为 \(3\)。
其余部分就和上面一样了。



