CF1066F 题解

CF1066F

题意

在一个平面上有 \(n\) 个点，第 \(i\) 个点的坐标为 \((x_i, y_i)\)，它的级别为 \(\max(x_i, y_i)\)。

最开始在 \((0, 0)\)。当级别为 \(i\) 的点全部走完后才可以走级别为 \(i + 1\) 的点。

两个点 \((x_1, y_1)\) 和 \((x_2, y_2)\) 之间的距离是 \(|x_1 - x_2| + |y_1 - y_2|\)。

请你求出走完所有的点的最短总距离。

思路

我们先思考一个问题，级别为 \(i\) 的点在平面直角坐标系上会是那些？

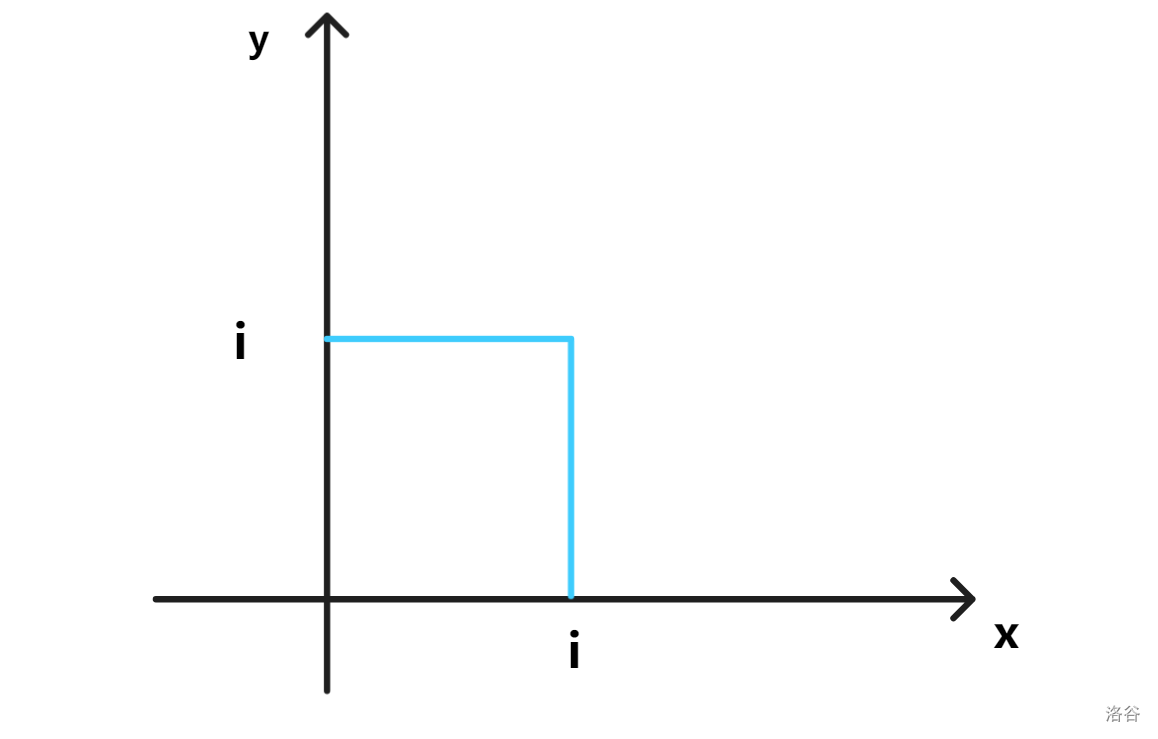
那么，可以发现，对于同一级别的点来说，要想用最短距离走完这些点的话，一定是从最左上的点走到最右下的点。

令 \(p_{i, 0 / 1}\) 表示级别为 \(i\) 的点最左上 / 最右下的点的编号，\(D(i, j)\) 表示编号为 \(i\) 和 \(j\) 的点之间的距离。

\(dp_{i, 0 / 1}\) 表示级别为 \(i\) 的点的这段路径最终停在最左上 / 最右下的点上的最短距离。

所以有转移为：

\[dp_{i, 0} = \min(dp_{i - 1, 0} + D(p_{i - 1, 0}, p_{i, 1}), dp_{i - 1, 1} + D(p_{i - 1, 1}, p_{i, 1})) + D(p_{i, 0}, p_{i, 1}) \]

\[dp_{i, 1} = \min(dp_{i - 1, 0} + D(p_{i - 1, 0}, p_{i, 0}), dp_{i - 1, 1} + D(p_{i - 1, 1}, p_{i, 0})) + D(p_{i, 0}, p_{i, 1}) \]