abc 233 题解
C - Product
题意
有 \(N\) 个序列,每个序列选择一个数字,请问有多少种选择方式可以让所有的数字的乘积为 \(X\)。
\(N \ge 2,L_i \ge 2\)
每个盒子中的球的数量的乘积至多为 \(10 ^ 5\)
思路
首先,我们可以看出来,这个题目可以用搜索来完成,但是问题就是,会不会 TLE 呢?
当然不会啦!!!
题目里有这么一句话:每个盒子中的球的数量的乘积至多为 \(10 ^ 5\) ,这就意味着最终的方案数最多也只有 \(10 ^ 5\)。
所以,搜索当然不会 TLE。
最后还有一个部分,那就是 一定要选择除法来做 ,如果当前的乘积为 \(10 ^ {18} - 1\) ,而要选择的 \(a_{i, j}\) 为 \(10 ^ 9\) 且 \(X\) 为 \(10 ^ {18}\),那么如果再乘上 \(a_{i j}\),就有 \(10 ^ {27}\) 那么大了,就 爆 long long 了。
D - Count Interval
题意
请你求出在长度为 \(N\) 的序列中有多少个字段的和为 \(K\)。
思路
首先,我们可以用前缀和来表示一个子段的和,也就是 \(s_r - s_{l - 1}\)。
所以题目的要求就是:
求出有多少对 \((l, r)\) ,使得 \(s_r - s_{l - 1} = k\),也就是 \(s_r = s_{l - 1} + k\)。
所以就有这么一种方法:
枚举所有的区间,判断是否满足条件。
但是,这样很明显时间复杂度为 \(O(n ^ 2)\),那么,应该如何优化呢?
对于 \(i\) 来说,\(s_{i - 1} + k\) 是一个定值,也就是说,只要提前算出在 \(i\) 之后的 \(s_{i - 1} + k\) 的数量即可。
E - Σ [k = 0..10 ^ 100] floor (X / 10 ^ k)
题意
请你求出
思路
首先,这道题目说是向下取整,所以如果输入是 1234,那么输出就是 1234 + 123 + 12 + 1 = 1370。
那么也就可以写成这样:
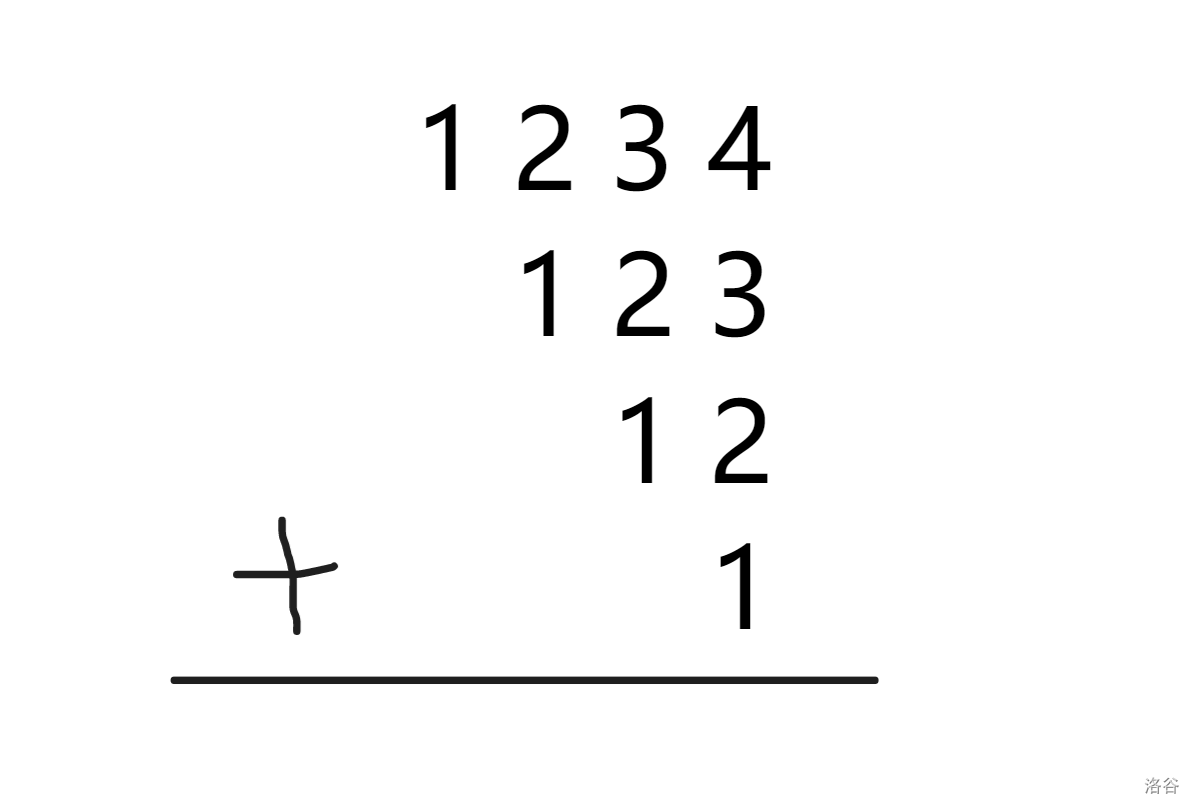
可以发现,最终答案的每一位其实就是对 \(X\) 求了一遍前缀和。
最后再处理一次进位即可。
F - Swap and Sort
题意
给定一个长度为 \(n\) 的全排列 \(P\),有 \(m\) 种操作,每种操作交换 \(a_i\) 和 \(b_i\) 。
请问可不可以用至多 \(5 \times 10 ^ 5\) 次操作,使得序列升序排序。
如果可以,输出操作序列,否则输出 -1。
思路
将 \(m\) 种操作看成一条无向边,那么题目就会变成这样:
给定一个 \(n\) 个点,\(m\) 条边的无向图,每次操作可以交换相邻两个点的数字 \(p_i, p_j\),请你求出需要多少次操作,使得所有 \(p_i = i\)。
所以,就有三种情况了,我们一一来看:
-
链:那么,很明显,我们会先考虑满足这条链的两端,因为满足这两个点后,只要对中间的一段进行操作即可。
-
树:树就和链很像,其实可以把链的两端看做成两个入度为 \(1\) 的点,那么每次优先操作的就是入度为 \(1\) 的点了。
-
图:既然我们都知道了树应该如何处理,那么我们就可以直接在图上搜出所有的树,再分别选择入度为 \(1\) 的点进行操作即可。
所以,直接按照这种来模拟即可。



