数据结构
栈
栈是一种先进后出的数据结构。
栈有两种实现方法,一种是数组,另外一种是 STL 容器。
- 数组:
int top, stk[N];
stk[++top] = x; // 入栈
top--; // 弹栈
int k = stk[top]; // 取栈顶
top = 0; // 清空栈
- STL:
stack<int> stk;
stk.push(x); // 入栈
stk.pop(); // 弹栈,此时栈不为空
int k = stk.top(); // 取栈顶,此时栈不为空
单调栈
单调栈,顾名思义,是栈内元素满足单调性的栈。
插入
假设我们现在的栈是这样的:
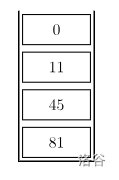
假设我们现在要把 \(14\) 压入栈中,那么就是这样的:
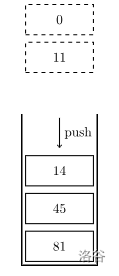
也就是说,我们将栈中那些比 \(14\) 小的元素都弹掉了。
实现就是这样的:
while (top && stk[top] < a[i]) top--;
stk[++top] = a[i];
使用
自然就是从栈顶读出来一个元素,该元素满足单调性的某一端。
例如举例中取出的即栈中的最小值。
队列
队列是一种先入先出的数据结构。
它像栈一样,也有数组和 STL 两种实现方法。
- 数组:
int h, t, que[N];
que[++t] = x; // 入队
h++; // 出队
int k = que[h]; // 访问队头
h = t = 0; // 清空队列
- STL:
queue<int> que;
que.push(x); // 入队
que.pop(); // 出队,此时队列不为空
int k = que.front(); // 访问队头,此时队列不为空
单调队列
我们先来看一道题:
给出一个长度为 \(n\) 的数组,输出每 \(k\) 个连续的数中的最大值。
首先,我们可以想到暴力,时间复杂度为 \(O(n \times k)\)。
但是,如果 \(n, k\) 都是 \(10 ^ 5\) 级别的数,是肯定会超时的,所以,我们需要单调队列来优化。
由于我们需要求的是最大值,所以,当队尾的元素比当前元素 \(x\) 还小的话,就直接把队尾的元素弹掉,再让 \(x\) 入队。
又因为我们需要维护的是长度为 \(k\) 的区间,所以,当 \(i\) 为右端点时,如果队头的元素 \(< i - k + 1\),就把队头弹掉。
void getmax() {
int h = 0, t = 0;
for (int i = 1; i < k; i++) {
while (h <= t && a[que[t]] <= a[i]) t--;
que[++t] = i;
}
for (int i = k; i <= n; i++) {
while (h <= t && a[que[t]] <= a[i]) t--;
que[++t] = i;
while (que[h] <= i - k) h++;
cout << a[que[h]] << ' ';
}
}
ST 表
ST 表是用于解决大部分 RMQ 问题的数据结构。
引入
给定 \(n\) 个数,\(m\) 次询问,每次回答 \([l, r]\) 中的最大值。
首先,我们可以想到一个暴力的做法:每次枚举 \(l \sim r\) 中的所有数字,求出最大值。
但是,当 \(n\) 足够大时,是会超时的。
所以就需要 ST 表了。
ST 表
ST 表基于倍增思想,\(O(n \log n)\) 预处理,\(O(1)\) 询问,但是不支持修改操作,线段树和树状数组可以修改元素。
我们先看前一部分,
预处理
我们定义 \(f_{i, j}\) 表示 \([i, i + 2 ^ j - 1]\) 的最大值,就有递推式:\(f_{i, j} = max(f_{i, j - 1}, f_{i + 2 ^ {j - 1}}, j - 1)\)。
void P() {
for (int j = 1; j < 20; j++) {
for (int i = 1; i + (1 << j) - 1 <= n; i++) {
f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
}
}
}
询问
我们可以发现,如果我们要求 \([l, r]\) 的最大值,其实就算所有合并的区间之间有重叠也没关系,也就是说,我们只需要求 \(max(f_{l, k}, f_{r - 2 ^ k + 1, k}) \ (2 ^ k \le r - l + 1)\) 即可,所以,我们需要预处理出所有 \(i \ (1 \le i \le n)\) 的 \(\log\)。
void P() {
for (int j = 1; j < L; j++) {
for (int i = 1; i + (1 << j) - 1 <= n; i++) {
f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
}
}
log_2[1] = 0;
for (int i = 2; i <= n; i++) {
log_2[i] = log_2[i / 2] + 1;
}
}
int Solve() {
int p = log_2[r - l + 1];
return max(f[l][p], f[r - (1 << p) + 1][p]);
}
并查集
用于合并集合和查询元素所属集合(两个元素是否属于同一集合)。
将每个集合看做成是一颗树,合并元素 \(u\) 和元素 \(v\) 的集合时,只需要将元素 \(u\) 所在的树的根结点变成元素 \(v\) 所在的树的根结点的父亲即可。
查询也是同样的,只需要查询两个元素所在的集合的根结点是否相同即可。
暴力
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, m, fa[N];
int Find(int t) { // 查询根结点
if (fa[t]) {
return Find(fa[t]);
}
return t;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
while (m--) {
int op, u, v;
cin >> op >> u >> v;
if (op == 1) {
u = Find(u), v = Find(v);
if (u != v) {
// 如果将自己连为自己的父亲的话,Find() 函数会无限递归
fa[u] = v;
}
} else {
cout << (Find(u) == Find(v) ? "Y\n" : "N\n");
}
}
return 0;
}
但是,在最坏的情况下,所有元素都在一个集合中,但是这颗树是一条链的话,会使得每次查询的时间达到 \(O(n)\),可能会超时,所以需要进行一些优化。
路径压缩
每次在查询根结点时,将这条路径上的所有元素的父亲结点都设成根节点。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10;
int n, m, op, x, y, fa[N];
int Find(int t) {
return fa[t] ? fa[t] = Find(fa[t]) : t;
// 将父亲结点设为根结点
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m;
while (m--) {
cin >> op >> x >> y;
if (op == 1) {
x = Find(x), y = Find(y);
if (x != y) {
fa[x] = y;
}
} else {
cout << (Find(x) == Find(y) ? 'Y' : 'N') << '\n';
}
}
return 0;
}
按秩合并(启发式合并)
按大小合并
证明:最开始,元素 \(i\) 在一个大小为 1 的集合中,考虑最坏情况,它会合并到一个大小为 2 的集合中,然后合并到一个大小为 4 的集合中……一个元素最多合并 \(\log n\) 次,所以 \(n\) 个元素合并的总时间复杂度为 \(O(n \times \log n)\)。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, m, fa[N], sz[N];
int Find(int t) {
return fa[t] ? Find(fa[t]) : t;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
fill(sz + 1, sz + n + 1, 1);
while (m--) {
int op, u, v;
cin >> op >> u >> v;
if (op == 1) {
u = Find(u), v = Find(v);
if (u != v) {
if (sz[u] > sz[v]) {
swap(u, v);
}
sz[v] += sz[u], fa[u] = v;
}
} else {
cout << (Find(u) == Find(v) ? "Y\n" : "N\n");
}
}
return 0;
}
按高度合并
时间复杂度也是 \(O(n \times \log n)\)。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, m, fa[N], h[N];
int Find(int t) {
return fa[t] ? Find(fa[t]) : t;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
while (m--) {
int op, u, v;
cin >> op >> u >> v;
if (op == 1) {
u = Find(u), v = Find(v);
if (u != v) {
if (h[u] > h[v]) {
swap(u, v);
}
if (h[u] == h[v]) {
h[u]++;
}
fa[u] = v;
}
} else {
cout << (Find(u) == Find(v) ? "Y\n" : "N\n");
}
}
return 0;
}
路径压缩 + 按秩合并
每次查询的时间复杂度为 \(O(\alpha (n))\),其中 \(\alpha (n)\) 指的是阿克曼函数的反函数,增长极慢,是一个很小的常数。
按大小合并
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, m, fa[N], sz[N];
int Find(int t) {
return (fa[t] ? fa[t] = Find(fa[t]) : t);
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
fill(sz + 1, sz + n + 1, 1);
while (m--) {
int op, u, v;
cin >> op >> u >> v;
if (op == 1) {
u = Find(u), v = Find(v);
if (u != v) {
if (sz[u] < sz[v]) {
swap(u, v);
}
sz[v] += sz[u], fa[u] = v;
}
} else {
cout << (Find(u) == Find(v) ? "Y\n" : "N\n");
}
}
return 0;
}
按高度合并
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, m, fa[N], h[N];
int Find(int t) {
return (fa[t] ? fa[t] = Find(fa[t]) : t);
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
while (m--) {
int op, u, v;
cin >> op >> u >> v;
if (op == 1) {
u = Find(u), v = Find(v);
if (u != v) {
if (h[u] > h[v]) {
swap(u, v);
}
if (h[u] == h[v]) {
h[u]++;
}
fa[u] = v;
}
} else {
cout << (Find(u) == Find(v) ? "Y\n" : "N\n");
}
}
return 0;
}
带权并查集
我们可以在每个并查集的边上设定某种权值,在路径压缩时需要将其合并,这样可以解决更多的问题。
洛谷 P2024
我们可以将同类关系的边权设为 0,捕食关系的边权设为 1,被捕食关系的边权设为 2,用一个数组来记录点 \(i\) 和点 \(i\) 的父亲的关系。
#include <bits/stdc++.h>
using namespace std;
const int N = 5e4 + 10;
int n, k, op, x, y, d[N], fa[N], ans;
int Find(int t) {
if (!fa[t]) {
return t;
}
int x = Find(fa[t]);
d[t] = (d[t] + d[fa[t]]) % 3, fa[t] = x;
return x;
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> k;
while (k--) {
cin >> op >> x >> y;
if ((x > n || y > n) || (op == 2 && x == y)) {
ans++;
} else {
int u = Find(x), v = Find(y);
op--;
if (u != v) { // 不属于同一个集合
int t = (op + d[y] - d[x] + 3) % 3;
fa[u] = v, d[u] = t; // d[u] 代表 u 和 fa[u] 的关系
} else {
int t = (d[x] - d[y] + 3) % 3;
// t 是集合内 x 和 y 的关系
ans += (t != op);
}
}
}
cout << ans;
return 0;
}
种类并查集
如果有 \(i\) 种不同的关系,就用 \(i\) 个并查集来维护一个元素和其他元素的关系。
洛谷 P2024
将吃自己的,被自己吃的,和自己同类的这三种关系分别存在三个并查集中,用结点 \(i, 2 \times i, 3 \times i\) 表示。
线段树
用来维护区间信息的数据结构,比如:区间最值,区间和等。
引入
首先,我们先思考这样一个问题:
给你一个长度为 \(n \ (1 \le n \le 10 ^ 5)\) 的序列 \(a\),有 \(m \ (1 \le m \le 10 ^ 5)\) 次询问,每次查询给定 \(l, r\),请你求出 \(l \sim r\) 的元素总和。
相信这个大家都会,用前缀和即可。
但是,如果有改变元素数值的操作呢?
如果我们将 \(a_p\) 改为 \(x\),那么在前缀和数组中,\(sum_p \sim sum_n\) 都会发生改变。
也就是说,在一个改变数值的操作中,我们最多会在前缀和数组上改变 \(n\) 个数值,那么,时间复杂度还是 \(O(n \times m)\),和暴力查找没有区别。
所以,这个时候,我们就需要用线段树来维护这些信息了。
基本结构
线段树本质上就是一棵树,每个结点代表一段区间。
假设我们现在有一个数组 \(a = \{10, 11, 12, 13, 14\}\),要维护区间和,那么,线段树就应该像这样:

也就是说,我们每次将一个大区间分成两段,再由两段小区间合并成这个大区间。
并且,二叉树本身有一种表示方法:结点 \(i\) 的两个儿子分别是 \(2 \times i, 2 \times i + 1\)。
所以我们可以靠这个来快速合并与查询儿子区间。
那么我们还是考虑上面那个问题,下面给出建树的代码:
int Make_tree(int i, int l, int r) {
if (l == r) {
return tr[i] = a[l];
}
int mid = (l + r) >> 1;
return tr[i] = Make_tree(i * 2, l, mid) + Make_tree(i * 2 + 1, mid + 1, r);
}
时间复杂度为 \(O(n)\)。
修改某个元素
由于我们修改的是某个指定结点的值,所以,我们可以发现,在每次递归的时候,肯定只有一个区间中包含这个下标,就不用递归两个区间了。
注意:在你修改完值之后退出时,记得一定要修改线段树中的元素!!!把它变成修改之后的和
代码大概就是这样的:
void modify(int i, int l, int r, int p, int x) {
if (l == r) {
tr[i] = x;
return ;
}
int mid = (l + r) >> 1;
p <= mid ? modify(i * 2, l, mid, p, x) : modify(i * 2 + 1, mid + 1, r, p, x);
tr[i] = tr[i * 2] + tr[i * 2 + 1];
}
时间复杂度为 \(O(\log n)\)。
求区间信息
本身,我们维护这个线段树就是为了求出区间信息,所以,我们应该怎么快速地求出这些信息呢?
假设我们要求出区间 \([ql, qr]\) 的元素之和,对于我们当前递归到的这个区间 \([l, r]\),分三种情况:
-
如果 \([l, r]\) 被 \([ql, qr]\) 完全包含,就可以直接加上这个区间的和,停止递归。
-
如果 \([l, r]\) 和 \([ql, qr]\) 完全没有交集,就直接退出。
-
否则,继续递归。
int Sum(int i, int l, int r, int ql, int qr) {
if (qr < l || ql > r) return 0;
// qr < l : ql ..... qr .... l .... r 查询区间在当前递归的区间的左边,没有交集
// ql > r : l ..... r .... ql .... qr 查询区间在当前递归的区间的右边,没有交集
if (ql <= l && r <= qr) return tr[i]; // 当前递归的区间被查询区间完全包含
int mid = (l + r) >> 1;
return Sum(i * 2, l, mid, ql, qr) + Sum(i * 2 + 1, mid + 1, rl, ql, qr);
}
区间修改和懒标记
如果,我们要改变的不是一个元素,而是很多元素呢?
譬如说,我们需要给 \([ql, qr]\) 的所有元素加上 \(k\),如果暴力枚举所有点做单点修改,还不如直接暴力修改元素的值,所以,我们需要快速的修改它们。
还是考虑当前递归的区间 \([l, r]\),就像我们刚才求区间信息一样,分三种情况讨论。
-
如果 \([l, r]\) 和 \([ql, qr]\) 没有交集,那么这次修改不会影响到这个区间,直接退出。
-
如果 \([l, r]\) 被 \([ql, qr]\) 完全包含,那么直接更改 \([l, r]\) 的和,并且将 \(k\) 打在懒标记上,停止递归。
-
否则,继续递归。
那么,这个懒标记到底是什么呢?
其实,因为我们是直接更改区间和,所以,\([l, r]\) 的子区间是没有进行改变的,那么,如果后面的查询操作查询到了 \([l, r]\) 的子区间,会对答案有影响,所以,我们需要一个懒标记来记录 \([l, r]\) 这一段还有多少值没有加给 \([l, r]\) 的子区间。
那么,我们在查询区间信息时,就需将每个区间的懒标记对应的值加到它的子区间上,我们称这个操作为懒标记下传。
注意:
-
懒标记所记录的是子区间需要加上的数值,并不需要加给区间本身。
-
懒标记是需要传给子区间的,也就是说,子区间的懒标记需要加上当前区间的懒标记,因为还要传给子区间的子区间(儿子的儿子)。
void update(int i, int l, int r, int k) {
lazy[i] += k, tr[i] += (r - l + 1) * k;
}
void pushdown(int i, int l, int mid, int r) { // 懒标记下传
update(i * 2, l, mid, lazy[i]), update(i * 2 + 1, mid + 1, r, lazy[i]), lazy[i] = 0;
}
void modify(int i, int l, int r, int ql, int qr, int k) {
if (qr < l || ql > r) return ;
if (ql <= l && r <= qr) {
tr[i] += (r - l + 1) * k, lazy[i] += k;
return ;
}
int mid = (l + r) >> 1;
pushdown(i, l, mid, r);
modify(i * 2, l, mid, ql, qr, k), modify(i * 2 + 1, mid + 1, r, ql, qr, k);
tr[i] = tr[i * 2] + tr[i * 2 + 1];
}
永久化标记
这大概是懒标记的一个不完全版本,可以维护的问题是比较有限的。
首先,我们先说一下什么是永久化标记。
假设,我们有两种操作,第一种是区间 \([l, r]\) 加上 \(x\),第二种是查询区间和。
假设原数组 \(a = \{1, 2, 3, 4, 5\}\),我们已经对 \([1, 4]\) 加上了 \(5\),那么,如果用懒标记实现,应该是这样的:

然后,我们下传标记:

但是如果我们使用的是永久化标记,就是这样的:

这样打标记的话,当我们查询的时候,只需要在从下往上回溯时加上对应的数值即可,相比于懒标记,减少了下传的过程,可以降低常数,并且似乎在一些撤销操作上有独特的优势。
但是永久化标记也有一些限制,如果我们交换操作顺序会改变结果的话,永久化标记大概率是无法维护的,这时,就还是得使用懒标记。
看一个例题:
abc342 G
题意
有一个长度为 \(n\) 的整数序列 \(a\),有 \(q\) 次操作,操作分为三种类型:
- 由三个整数 \((l, r, x)\) 表示,用 \(max(a_i, x)\) 替换 \(a_i \ (l \le i \le r)\)。
- 由一个整数 \(i\) 表示,撤销第 \(i\) 次操作,保证第 \(i\) 次操作是 1 操作并且尚未取消。
- 由一个整数 \(i\) 表示,输出当前的 \(a_i\)。
思路
我们考虑使用永久化标记,也就是说,对于区间 \([l, r]\) 所对应的每一个区间,都用 \(x\) 更新标记。
但是,由于我们需要撤销操作,又需要维护标记中的最大值,所以我们可以用 set 维护标记,在撤销时 erase 掉标记,修改时 insert 标记。
这种撤销的操作用永久化标记维护会更加方便,因为如果使用懒标记,通常在撤销时,这次操作的影响已经下传了,也就是说,我们需要多对很多结点进行撤销操作,就无法保证时间复杂度了。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
struct Node {
int l, r, x;
} que[N];
int n, a[N], op, q;
multiset<int> tr[4 * N];
void build(int i, int l, int r) {
if (l == r) {
tr[i].insert(a[l]); return ;
}
int mid = (l + r) >> 1;
build(i * 2, l, mid), build(i * 2 + 1, mid + 1, r);
}
void modify(int i, int l, int r, int ql, int qr, int x, int k) {
if (qr < l || ql > r) return ;
if (ql <= l && r <= qr) {
if (!k) tr[i].insert(x);
else tr[i].erase(tr[i].find(x));
return ;
}
int mid = (l + r) >> 1;
modify(i * 2, l, mid, ql, qr, x, k), modify(i * 2 + 1, mid + 1, r, ql, qr, x, k);
}
int query(int i, int l, int r, int p) {
if (l == r) return *tr[i].rbegin();
int mid = (l + r) >> 1;
int k = (p <= mid ? query(i * 2, l, mid, p) : query(i * 2 + 1, mid + 1, r, p));
return tr[i].empty() ? k : max(k, *tr[i].rbegin());
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
build(1, 1, n);
cin >> q;
for (int i = 1; i <= q; i++) {
cin >> op;
if (op == 1) {
int l, r, x; cin >> l >> r >> x;
que[i] = {l, r, x};
modify(1, 1, n, l, r, x, 0);
} else if (op == 2) {
int x; cin >> x;
modify(1, 1, n, que[x].l, que[x].r, que[x].x, 1);
} else {
int x; cin >> x;
cout << query(1, 1, n, x) << '\n';
}
}
return 0;
}
线段树优化建图
先看一个例题
CF786B
题意
有一个 \(n\) 个点的有向图,有 \(q\) 个操作,操作分为三种:
- 有一条从 \(u\) 到 \(v\)的边, 边权为 \(w\)。
- \(u\) 到区间 \([l, r]\) 的每个点都有一条边,边权为 \(w\)。
- 区间 \([l, r]\) 的每个点都有一条到 \(u\) 的边,边权为 \(w\)。
请在 \(q\) 次操作结束后,求出从 \(1\) 到 \(i \ (1 \le i \le n)\) 的最小距离。
思路
首先,我们可以想到暴力的对于每个 2, 3 操作连边,但是显然,这样时间复杂度是 \(O(q \times n)\) 的,不够优秀。
由于我们是对区间连边,所以可以考虑用线段树优化建图。

很显然的,图中每一条绿色的边的边权都应该是 \(0\),但是,如果我们真的像这样直接连每条绿色的双向边,最终答案就会全为 \(0\),所以,我们可以考虑用两颗线段树连边,一颗线段树维护从儿子到父亲的边,另一颗线段树维护从父亲到儿子的边:
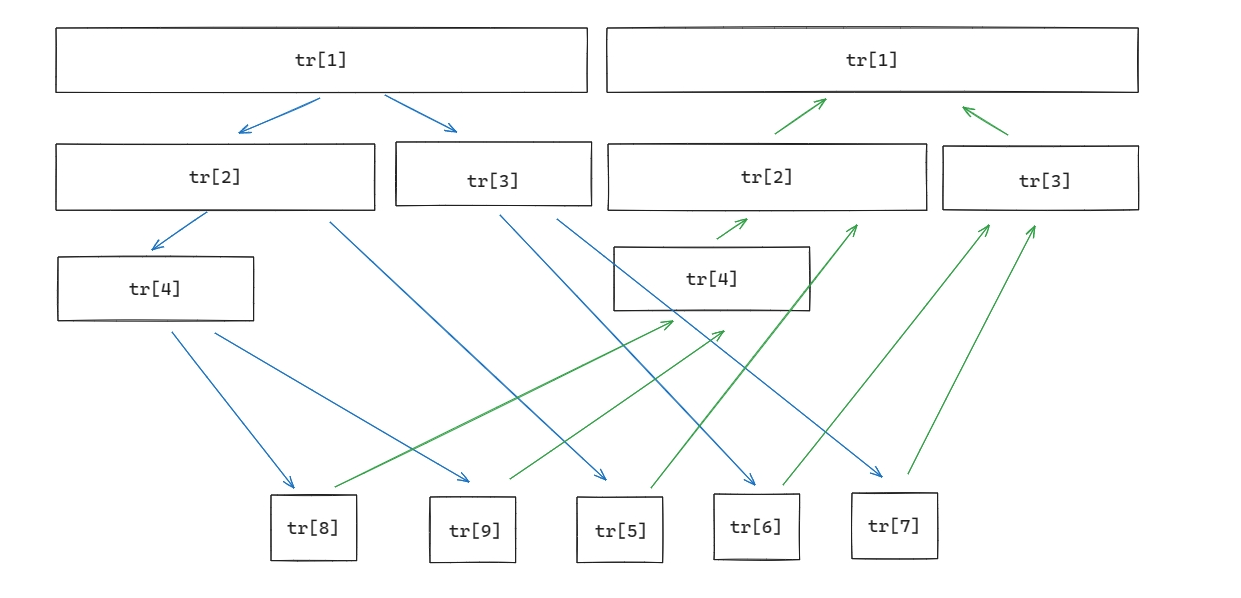
当然,我们要让两颗线段树的编号不同,所以,我们可以这样编号:

void build(int i, int l, int r, int k) {
if (l == r) {
f[i] = h[i] = l;
return ;
}
int mid = (l + r) >> 1;
if (!k) f[i] = ++cnt;
else h[i] = ++cnt;
build(i * 2, l, mid, k), build(i * 2 + 1, mid + 1, r, k);
if (!k) g[f[i]].push_back({f[i * 2], 0}), g[f[i]].push_back({f[i * 2 + 1], 0}); // 从父亲到儿子
else g[h[i * 2]].push_back({h[i], 0}), g[h[i * 2 + 1]].push_back({h[i], 0}); // 从儿子到父亲
}
然后,我们就可以用类似线段树查询的方式对区间建边了。
void Add_Edge(int i, int l, int r, int ql, int qr, int x, int k, int w) {
if (qr < l || ql > r) return ;
if (ql <= l && r <= qr) {
if (!k) g[x].push_back({f[i], w});
else g[h[i]].push_back({x, w});
return ;
}
int mid = (l + r) >> 1;
Add_Edge(i * 2, l, mid, ql, qr, x, k, w), Add_Edge(i * 2 + 1, mid + 1, r, ql, qr, x, k, w);
}
然后就可以正常的跑一遍 \(Dijkstra\) 了,但是,在这里有一个特别需要注意的点,就是每个数组的大小,譬如说,你建好两颗线段树后总结点数量会达到 \(8 \times n\) 的级别。
代码
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5 + 10;
struct Node {
int v;
ll w;
bool operator < (const Node &i) const {
return w > i.w;
}
};
int n, q, s, cnt, f[4 * N], h[4 * N]; // f : down h : up
ll d[8 * N];
vector<Node> g[8 * N];
priority_queue<Node> pq;
void build(int i, int l, int r, int k) {
if (l == r) {
f[i] = h[i] = l;
return ;
}
int mid = (l + r) >> 1;
if (!k) f[i] = ++cnt;
else h[i] = ++cnt;
build(i * 2, l, mid, k), build(i * 2 + 1, mid + 1, r, k);
if (!k) g[f[i]].push_back({f[i * 2], 0}), g[f[i]].push_back({f[i * 2 + 1], 0});
else g[h[i * 2]].push_back({h[i], 0}), g[h[i * 2 + 1]].push_back({h[i], 0});
}
void Add_Edge(int i, int l, int r, int ql, int qr, int x, int k, int w) {
if (qr < l || ql > r) return ;
if (ql <= l && r <= qr) {
if (!k) g[x].push_back({f[i], w});
else g[h[i]].push_back({x, w});
return ;
}
int mid = (l + r) >> 1;
Add_Edge(i * 2, l, mid, ql, qr, x, k, w), Add_Edge(i * 2 + 1, mid + 1, r, ql, qr, x, k, w);
}
void Dijkstra() {
fill(d + 1, d + 8 * n + 1, 1e18);
d[s] = 0, pq.push({s, 0});
while (!pq.empty()) {
Node u = pq.top(); pq.pop();
if (u.w != d[u.v]) continue;
for (Node v : g[u.v]) {
if (d[v.v] > u.w + v.w) {
d[v.v] = u.w + v.w;
pq.push({v.v, d[v.v]});
}
}
}
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> q >> s, cnt = n;
build(1, 1, n, 0), build(1, 1, n, 1);
for (int i = 1; i <= q; i++) {
int op; cin >> op;
if (op == 1) {
int u, v, w; cin >> u >> v >> w;
g[u].push_back({v, w});
} else {
int u, l, r, w; cin >> u >> l >> r >> w;
Add_Edge(1, 1, n, l, r, u, op - 2, w);
}
}
Dijkstra();
for (int i = 1; i <= n; i++) {
cout << (d[i] == 1e18 ? -1ll : d[i]) << ' ';
}
return 0;
}
所以,总结一下,线段树优化建图主要就是用在对区间建边的情况上,有时候可能要建一些中间点,也就是对多个点到多个点建边时,可以用中间点向两个点集中的所有点分别建边,就像是 洛谷 P1983 所用的建图优化一样。
树状数组
前言:树状数组可以做的事情基本上线段树都可以做到,只要题目不卡常,用线段树基本都能做。
初步感知
我们先举个例子,如果我们想知道 \(a[1 \dots 7]\) 的和,应该怎么办?
当然可以直接暴力枚举前七个数,相加。
但是如果我们知道 \(A = a_1 + a_2 + a_3 + a_4, B = a_5 + a_6, C = a_7\),那么答案就是 \(A + B + C\)。
所以我们可以得到一个结论:我们总能把 \([1, n]\) 拆成 不多于 \(\boldsymbol{\log n}\) 段区间,使得这 \(\log n\) 段区间的信息是 已知的。
所以,我们只需要合并 \(\log n\) 段区间的信息就可以了。
区间管辖范围

我们可以发现,\(c\) 就是存储某些元素的前缀和的数组,那么,我们应该如何知道 \(c_i\) 管辖的范围呢?
在树状数组中,规定 \(c_i\) 的管辖范围是 \(2 ^ k\),其中 \(k\) 是 \(i\) 的二进制中最低位的 \(1\) 的位数。
我们记 \(lowbit(i)\) 表示 \(i\) 的二进制中最低位的 \(1\) 的位数。
那么,这个 \(2 ^ k\) 应该怎么求呢?
我们定义 \(lowbit(i)\) 表示 \(i\) 的最低位的 \(1\) 以及后面的 \(0\) 所组成的数。
所以,根据我们的位运算知识,可以发现 lowbit(x) = x & -x。
int lowbit(int x) {
return x & (-x);
}
建树
\(O(n)\) 建树。
方法一:
每一个节点的值是由所有与自己直接相连的儿子的值求和得到的。因此可以倒着考虑贡献,即每次确定完儿子的值后,用自己的值更新自己的直接父亲。
void init() {
for (int i = 1; i <= n; i++) {
t[i] += a[i];
int j = i + lowbit(i);
if (j <= n) t[j] += t[i];
}
}
方法二:
由于 \(c_i\) 管辖的是 \([i - lowbit(i) + 1, i]\),所以我们可以维护一个前缀和数组 \(sum\) 来计算 \(c\) 数组。
void init() {
for (int i = 1; i <= n; i++) {
t[i] = sum[i] - sum[i - lowbit(i)];
}
}
区间查询
我们来举个例子,如果我们要求出区间 \([3, 7]\) 的和,应该怎么办呢?
我们可以求出 \([1, 7]\) 的前缀和与 \([1, 2]\) 的前缀和,再相减即可。
所以,有时候,我们可以把区间问题变成前缀问题来解决。
那么,我们应该怎么用树状数组来求出前缀和呢?
由于 \(c_i\) 管辖的区间是 \([i - lowbit(i) + 1, i]\),所以下一个需要合并的区间的右端点是 \(i - lowbit(i)\),那么,我们只要每次都这样暴力的跳,然后边跳边合并 \(c\) 就可以求出前缀和。
时间复杂度为 \(O(\log n)\)。
int getans(int x) {
int ret = 0;
while (x > 0) ret += tr[x], x -= lowbit(x);
return ret;
}
单点修改
那么,如果我们需要修改 \(a_x\) 呢?
修改 \(a_x\) 自然会让那些包含 \(a_x\) 的 \(c_i\) 的答案变化,所以,我们应该如何找到这些 \(i\) 呢?
显然,在树状数组所建成的这棵树上,\(i\) 是 \(x\) 的祖先,所以,我们只需要不停的找父亲,然后改变 \(c_i\) 就可以了。
时间复杂度为 \(O(\log n)\)。
void modify(int x, int k) {
while (x <= n) tr[x] += k, x += lowbit(x);
}
既然我们学会了单点修改,那么我们就可以把建树的过程变成 \(n\) 次区间修改,时间复杂度为 \(O(n \times \log n)\)。
区间修改,单点查询
我们不维护原数组,而是考虑维护差分数组,由于差分数组在处理区间修改上非常方便,只需要在 \(l, r + 1\) 两个点上分别进行修改,并且通过差分数组还原原数组的方式就是前缀和,刚好符合树状数组只能维护前缀和和单点修改的性质,在某些时候可以以优秀的常数和较短的码量代替线段树。
void modify(int x, int k) {
while (x <= n) tr[x] += k, x += lowbit(x);
}
void Modify(int l, int r, int x) {
modify(l, x), modify(r + 1, -x);
}
int getans(int x) {
int ret = 0;
while (x > 0) ret += tr[x], x -= lowbit(x);
return ret;
}
区间修改,区间查询
我们的思路还是将在原序列 \(a\) 上的操作转成在差分数组 \(d\) 上的操作。
先考虑区间查询,拿查询区间和为例,将区间和转换为两个前缀和:\(\sum\limits_{i = l} ^ r a_i = \sum\limits_{i = 1} ^ {r} a_i - \sum\limits_{i = 1} ^ {l - 1} a_i\)。
由于每一个 \(a_i = \sum\limits_{j = 1} ^ i d_j\),所以 \(\sum\limits_{i = 1} ^ r = \sum\limits_{i = 1} ^ r \sum\limits_{j = 1} ^ i d_j = \sum\limits_{i = 1} ^ r (r - i + 1)d_i = (r + 1)\sum\limits_{i = 1} ^ r d_i - \sum\limits_{i = 1} ^ r i \cdot d_i\)
因此,我们只需要分别用两个树状数组维护 \(d_i\) 与 \(i \cdot d_i\) 的信息即可。
我们再考虑区间修改,同样的,由于是维护差分数组,我们只需要对 \(l, r + 1\) 进行修改。
首先,\(d_i\) 的维护和前面是一样的。
而 \(i \cdot d_i\) 的维护也只是在 \(l\) 的位置加上 \(l \cdot x\),并在 \(r + 1\) 的位置减去 \((r + 1) \cdot x\)。
int lowbit(int x) {
return x & (-x);
}
void modify(int x, ll k, int tp) {
while (x <= n) (!tp ? tr[x] : _tr[x]) += k, x += lowbit(x);
}
ll getans(int x, int tp) {
ll ret = 0;
while (x > 0) ret += (!tp ? tr[x] : _tr[x]), x -= lowbit(x);
return ret;
}
void Modify(int x, int y, int k) {
modify(x, k, 0), modify(y + 1, -k, 0);
modify(x, 1ll * x * k, 1);
modify(y + 1, -1ll * (y + 1) * k, 1);
}
ll getsum(int x) {
return (x + 1) * getans(x, 0) - getans(x, 1);
}
ll query(int x, int y) {
return getsum(y) - getsum(x - 1);
}



