字符串
字符串
概念
令 \(|s|\) 为 \(s\) 的长度。
-
子串:字符串 \(s\) 中任意的连续的一段被称为 \(s\) 的子串,特别地,空串也是 \(s\) 的子串。
-
前缀:字符串 \(s\) 中的任意一个从 \(1\) 开始的子串被称为 \(s\) 的前缀。
-
后缀:字符串 \(s\) 中的任意一个末尾为 \(|s|\) 的子串被称为 \(s\) 的后缀。
-
border:既是 \(s\) 的前缀又是 \(s\) 的后缀的字符串就是 \(s\) 的一个 border。
-
周期:令 \(p\) 为 \(s\) 的周期,那么对于 \(1 \le i \le |s| - p\),都有 \(s_i = s_{i + p}\)。
用 pre(s, k) 表示 \(s\) 的长度为 \(k\) 的前缀,suf(s, k) 表示 \(s\) 的长度为 \(k\) 的后缀。
border 与周期
当 \(s\) 的长度为 \(k\) 的前缀为 \(s\) 的 border 时,\(|s| - k\) 一定是 \(s\) 的周期。
border 的传递性
1.\(s\) 是 \(t\) 的 border,\(t\) 是 \(r\) 的 border,那么 \(s\) 是 \(r\) 的 border。
2.\(s\) 是 \(r\) 的 border,\(t \ (|t| > |s|)\) 是 \(r\) 的 border,那么 \(s\) 是 \(t\) 的 border。
所以,我们用 mb(s) 表示 \(s\) 的最长 border,那么,\(s\) 的所有 border 就分别为 mb(s),mb(mb(s)) ……。
KMP
单模匹配算法,在一个文本串 \(s\) 中查找一个模式串 \(t\),计算复杂度为 \(O(|s| + |t|)\),是此类算法可以达到的最优复杂度,空间复杂度也很优秀,为 \(O(|s|)\)。
令 \(|s| = n, |t| = m\)。
暴力
枚举 \(1 \le i \le n\),暴力往后找 \(m\) 个字符,判断是否与 \(t\) 相等,时间复杂度为 \(O(n \times m)\)。
正解
由于我们的暴力在每次碰到一个不一样的字符(也就是失配)时,就会重头开始配对,会浪费很多时间去重复判断已经判断过的字符,而 kmp 就可以很好的解决这个问题。
我们用两个指针 \(i, j\) 分别表示当前匹配到 \(s\) 中的第 \(i\) 个字符, \(t\) 中的第 \(j\) 个字符了。
我们先举个例子:
s : a b a b a b a d b a b
t : a b a b a c b
我们会在 \(i = j = 6\) 时失配,这个时候,暴力做法会回到 \(i = 2, j = 1\),但是,我们其实可以直接这样做:
s : a b a b a b a d b a b
t : a b a b a c b
因为 aba 是 ababa 的最长 border,所以我们可以直接将 \(j\) 挪到 \(4\),这样就相当于前缀需要挪到原来的某个后缀上,又要使得这个前缀和后缀相等,自然就是挪到 border 后一个啦。
失配数组(最长 border 长度)
令当前要求 pre(s, i) 的最长 border 长度,用 \(nxt_i\) 表示。
那么令 pre(s, i - 1) 的所有 border 的长度分别为 \(k_1, k_2, k_3, \dots ,k_m \ (k_1 > k_2 > k_3 > \dots > k_m)\),那么,我们就是需要找到一个最大的 \(k_j\),使得 \(s_{k_j + 1} = s_i\)。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
string s1, s2;
int nxt[N];
void get_fail() {
int k = 0;
nxt[1] = 0;
for (int i = 2; i < s2.size(); i++) {
while (k && s2[i] != s2[k + 1]) {
k = nxt[k];
}
k += (s2[i] == s2[k + 1]), nxt[i] = k;
}
}
void KMP() {
int n = s1.size() - 1, m = s2.size() - 1;
for (int i = 1, j = 0; i <= n; i++) {
while (j && s1[i] != s2[j + 1]) {
j = nxt[j];
}
j += (s1[i] == s2[j + 1]);
if (j == m) {
cout << i - m + 1 << '\n', j = nxt[j];
}
}
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> s1 >> s2, s1 = ' ' + s1, s2 = ' ' + s2;
get_fail(), KMP();
for (int i = 1; i < s2.size(); i++) {
cout << nxt[i] << ' ';
}
return 0;
}
失配树
失配树就是用 nxt 数组建成的树。
性质
在失配树上,\(u, v\) 的最近公共祖先就是 pre(s, u) 和 pre(s, v) 的最长公共 border。
\(u, v\) 的所有祖先都是 pre(s, u) 和 pre(s, v) 的公共 border。
字符串哈希
其实本质上就是将字符串映射到了一个值上面,由于比较数值是 \(O(1)\) 的,所以我们可以用这种方式加快字符串的比较。
转化方法:
选择一个比字符集大小要大的数 \(p\),将每个字符串看作成 \(p\) 进制下的数,求值。
通常来说,\(p\) 会取 \(31, 131, 1313, 13131, 131313\) 等。
这里,特别要注意,求出来的值是需要取模的,因为当字符集的大小足够大或者字符串的长度足够长时,转化出来的值会很大,如果直接存下来,会逐渐丧失 \(O(1)\) 比较大小的优势。
哈希方法
-
自然溢出方法:令 \(M = 2 ^ {64}\)(\(M\) 为模数),那么,可以直接用
unsigned long long来存储数值,因为unsigned long long所能表示的范围是 \(0 \sim 2 ^ {64} - 1\),刚好就是对 \(2 ^ {64}\) 取模后可能得到的余数的范围。 -
单哈希方法:自己选择模数取模。
-
双哈希方法:选择两个模数取模,得到两个 Hash 值,提高安全性。
获取子串的哈希值
令 \(n = |s|\), H(t) 表示 \(t\) 的 Hash 值, \(Hash_i\) 为 pre(s, i) 的 Hash 值。
很明显,我们可以 \(O(n)\) 求出 \(s\) 的所有前缀的 Hash 值,那么,我们可以用一种类似于前缀和的思想得到 \(s\) 中 \([l, r]\) 这个子串的 Hash 值。
比如说:\(H(de) = H(abcde) - H(abc) \times p ^ 2\)。
那么,可以写这样一个函数来获取任意一个子串的 Hash 值:
using ull = unsigned long long;
void get_P() {
for (int i = 1; i <= n; i++) {
P[i] = P[i - 1] * p % M;
}
}
ull get_Hash(int i, int j) {
return ((Hash[j] - Hash[i - 1] * P[j - i + 1]) % M + M) % M;
}
哈希求最长回文子串
暴力
枚举每个字符作为回文串的中心,分别向左边和右边进行扩展,时间复杂度为 \(O(|s| ^ 2)\)。
正解
枚举每个字符作为回文串的中心,二分左边和右边的长度,时间复杂度为 \(O(|s| \times \log |s|)\)
代码
#include <bits/stdc++.h>
using namespace std;
using ull = unsigned long long;
const int N = 1010;
string s;
int p = 131, n, ans;
ull P[N], a[N], b[N];
void get_P() {
P[0] = 1;
for (int i = 1; i <= n; i++) {
P[i] = P[i - 1] * p;
}
}
ull Hash(int l, int r, bool f) {
if (!f) {
return a[r] - a[l - 1] * P[r - l + 1];
}
return b[l] - b[r + 1] * P[r - l + 1];
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
getline(cin, s), n = s.size(), s = ' ' + s;
get_P();
for (int i = 1; i <= n; i++) {
a[i] = a[i - 1] * p + s[i];
}
for (int i = n; i >= 1; i--) {
b[i] = b[i + 1] * p + s[i];
}
for (int i = 1, l, r; i <= n; i++) {
if (i < n && s[i] == s[i + 1]) {
l = 0, r = min(i, n - i);
while (l < r) {
int mid = (l + r + 1) >> 1;
if (Hash(i - mid + 1, i, 0) == Hash(i + 1, i + mid, 1)) {
l = mid;
} else {
r = mid - 1;
}
}
ans = max(ans, 2 * l);
}
l = 0, r = min(i, n - i);
while (l < r) {
int mid = (l + r + 1) >> 1;
if (Hash(i - mid, i - 1, 0) == Hash(i + 1, i + mid, 1)) {
l = mid;
} else {
r = mid - 1;
}
}
ans = max(ans, 2 * l + 1);
}
cout << ans;
return 0;
}
字典树(Trie)
先看一张图(来自 oi-wiki):
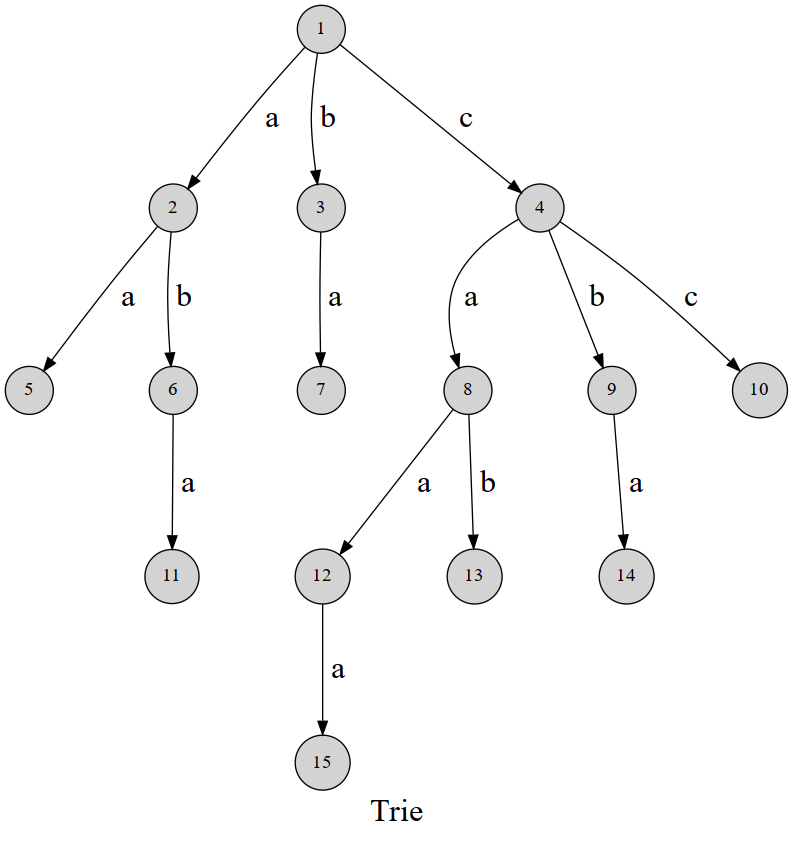
我们让每条边都代表一个字母,所以从根结点到任意一个结点的路径都是一个字符串。
因此,我们需要一个数组来记录每个结点是否有某条代表字母 \(c\) 的边,如果没有,就加上这条边,否则,直接跳到这条边指向的结点。
查找字符串
查询某个字符串是否出现过。
Trie 的时间复杂度为 \(O(n)\),\(n\) 代表所有字符串的字符总数。
暴力
把所有字符串存到 map 或 set 中,判断是否出现过。
(其实好像不算暴力)
正解
对所有字符串建 Trie,再在 Trie 中查询。
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
int n, m, f[N][30], c;
bool v[N], vis[N];
void Insert(string s) {
int root = 0;
for (int i = 0; i < s.size(); i++) {
if (!f[root][s[i] - 'a']) {
f[root][s[i] - 'a'] = ++c;
}
root = f[root][s[i] - 'a'];
}
v[root] = 1; // 从根结点到 root 的路径是一个字符串
}
void Find(string s) {
int root = 0;
for (int i = 0; i < s.size(); i++) {
root = f[root][s[i] - 'a'];
if (!root) { // 找不到了
cout << "WRONG\n";
return ;
}
}
if (!v[root]) {
cout << "WRONG\n";
} else {
cout << "OK\n";
}
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
while (n--) {
string s;
cin >> s, Insert(s);
}
cin >> m;
while (m--) {
string s;
cin >> s, Find(s);
}
return 0;
}
同样的,我们可以用字典树查找当前字符串是不是某个字符串的前缀。
#include <bits/stdc++.h>
using namespace std;
const int N = 3e6 + 10;
int T, n, q, c, sz[N], f[N][75];
int ID(char a) {
return 'a' <= a && a <= 'z' ? a - 'a' : ('A' <= a && a <= 'Z' ? 26 + a - 'A' : 52 + a - '0');
}
void Insert(string s) {
int root = 0;
for (int i = 0; i < s.size(); i++) {
int t = ID(s[i]);
if (!f[root][t]) {
f[root][t] = ++c;
}
root = f[root][t], sz[root]++; // sz 表示从跟结点到 root 是这条路径是多少个字符串的前缀
}
}
void Find(string s) {
int root = 0;
for (int i = 0; i < s.size(); i++) {
root = f[root][ID(s[i])];
if (!root) {
break;
}
}
cout << sz[root] << '\n';
}
void Solve() {
cin >> n >> q, c = 0;
while (n--) {
string s;
cin >> s, Insert(s);
}
while (q--) {
string s;
cin >> s, Find(s);
}
for (int i = 0; i <= c; i++) {
for (int j = 0; j < 75; j++) {
f[i][j] = 0;
}
sz[i] = 0;
}
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> T;
while (T--) {
Solve();
}
return 0;
}
后缀数组
定义
将一个字符串的所有后缀按照字典序从小到大排序,得到的排列就是后缀数组。
我们举一个例子:
banana 这样一个字符串,它的后缀有:
a,na,ana,nana,anana,banana
按照字典序排序后就是:
a
ana
anana
banana
na
nana
对于长度为 \(n\) 的字符串 \(s\),我们定义后缀 \(i\) 代表 \(s_i ... s_n\)。
那么 banana 的后缀数组 \(sa = \{6, 4, 2, 1, 5, 3\}\)(下标也可以从 \(0\) 开始)
后缀数组怎么求?
首先先介绍两个数组:\(sa\) 和 \(rnk\)
\(sa_i\) 表示后缀排序后第 \(i\) 小的后缀的编号,也就是我们的后缀数组。
\(rnk_i\) 表示后缀 \(i\) 的排名。
\(O(n ^ 2 \times \log n)\)
这个就是最简单的暴力,将每个字符串取出来直接排序,用默认的一个一个字符比较的方式比较每一个字符串。
\(O(n \times \log ^ 2 n)\)
做法一:
我们上面提到过,默认的字符串比较方式是一个一个字符比较的,但是比较两个字符串就需要 \(O(n)\) 的时间,太慢了,有没有什么办法提高效率呢?
我们先回忆一下字典序是如何比较的:
从 \(i = 1\) 开始,一直找,直到 \(s_i \ne t_i\)。
那么我们就需要快速找到第一个 \(s_i \ne t_i\) 的 \(i\),也就是说,\(s_1 ... s_{i - 1}\) = \(t_1 ... t_{i - 1}\)。
所以我们可以二分这个 \(i\),只需要判断两个字符串的前缀是否相等即可。
由于参与排序的字符串都是一个字符串的后缀,所以其实这些字符串的前缀都对应着原字符串的一个子串,可以用哈希求出一个子串的哈希值,直接进行比较。
void F() { // 预处理前缀的哈希值
for (int i = 1; i <= n; i++) {
h[i] = (h[i - 1] * p % mod + s[i] - 'a' + 1) % mod;
P[i] = P[i - 1] * p % mod;
}
}
ll Hash(int l, int r) { // 求子串的哈希值
return (h[r] - h[l - 1] * P[r - l + 1] % mod + mod) % mod;
}
bool cmp(const int &i, const int &j) { // 比较器
int l = 0, r = min(n - i + 1, n - j + 1);
while (l < r) {
int mid = (l + r + 1) >> 1;
Hash(i, i + mid - 1) == Hash(j, j + mid - 1) ? l = mid : r = mid - 1;
}
return s[i + l] == s[j + l] ? i > j : s[i + l] < s[j + l];
}
做法二:
这个过程要用到倍增的思想。
我们还是举 banana 这个例子:

上图中粉色的部分作为第一关键字,蓝色的部分作为第二关键字。
我们就可以根据关键字直接 sort,排出当前的顺序。
然后再根据现在的顺序推出下一次的第一第二关键字,再排序。
直到长度超过 \(n\)。
cin >> s, n = s.size();
for (int i = 0; i < n; i++) rnk[i] = s[i], sa[i] = i;
for (int t = 1; t < n; t *= 2) {
// temp 存的分别是第一关键字和第二关键字
for (int i = 0; i < n; i++) temp[i] = {rnk[i], i + t < n ? rnk[i + t] : -1};
sort(sa, sa + n, [](int i, int j) {return temp[i] < temp[j];});
for (int i = 0; i < n; i++) {
if (i > 0 && temp[sa[i]] == temp[sa[i - 1]]) rnk[sa[i]] = rnk[sa[i - 1]];
else rnk[sa[i]] = i;
}
}
for (int i = 0; i < n; i++) cout << sa[i] << ' ';
\(O(n \times \log n)\)
我们可以发现,上面那种倍增的做法会有两个 \(log\) 是因为中间有一次 sort 是 \(O(n \times \log n)\) 的。
那么如果我们可以 \(O(n)\) 将 \(temp\) 排序的话,就可以实现 \(O(n \times \log n)\) 求后缀数组了。
由于我们排序时的两个关键字的值域都在 \(1 \sim n\),那么就可以用基数排序实现 \(O(n)\) 排序了。
基数排序
首先,我们将所有数都扔进一个桶里面。
假设我们要给数组 \(a = \{1, 1, 4, 5, 1, 4\}\) 排序,那么扔进桶后,就应该是这样的 \(sum = \{3, 0, 0, 2, 1\} \ (1 \sim 5)\)。
我们再对桶做前缀和:\(sum = \{3, 3, 3, 5, 6\}\)。
然后从后往前遍历原数组 \(a\),首先是 \(a_6\),值是 \(4\),再看一下 \(sum_6\),是 \(5\),所以就把 \(a_6\) 放在新数组 \(b\) 的第 \(5\) 个,同时 \(sum_6\) 变成 \(4\)。
像上面所说的一样,我们从 \(n\) 到 \(1\) 依次放入数组 \(b\),就可以得到排序后的结果,并且这个结果是稳定的。
for (int i = 1; i <= n; i++) sum[a[i]]++;
for (int i = 1; i <= MAXA; i++) sum[i] += sum[i - 1];
for (int i = n; i >= 1; i--) b[sum[a[i]]--] = a[i];
// 这里需要注意下标是从 1 开始还是从 0 开始
memset(sum, 0, sizeof sum);
我们只需要分别对第二关键字和第一关键字排序即可。
cin >> s, n = s.size();
for (int i = 0; i < n; i++) rnk[i] = s[i], sa[i] = i;
for (int t = 1; t < n; t *= 2) {
for (int i = 0; i < n; i++) temp[i] = {rnk[i], i + t < n ? rnk[i + t] : 0};
for (int i = 0; i < n; i++) sum[temp[i].second]++;
for (int i = 1; i < N; i++) sum[i] += sum[i - 1];
for (int i = n - 1; i >= 0; i--) a[--sum[temp[sa[i]].second]] = sa[i];
fill(sum, sum + N, 0);
for (int i = 0; i < n; i++) sum[temp[i].first]++;
for (int i = 1; i < N; i++) sum[i] += sum[i - 1];
for (int i = n - 1; i >= 0; i--) sa[--sum[temp[a[i]].first]] = a[i];
fill(sum, sum + N, 0);
for (int i = 0; i < n; i++) {
if (i > 0 && temp[sa[i]] == temp[sa[i - 1]]) rnk[sa[i]] = rnk[sa[i - 1]];
else rnk[sa[i]] = i + 1;
}
}
\(O(n)\)
其实这种我不会,但是还是贴一个别人的板子吧
#include <stdio.h>
#include <string.h>
#define MAGIC(XD){\
memset(sa, 0, sizeof(int) * n);\
memcpy(x, c, sizeof(int) * z);\
XD\
memcpy(x + 1, c, sizeof(int) * (z - 1));\
for (i = 0; i < n; ++i) {\
if (sa[i] && !t[sa[i] - 1]) sa[x[s[sa[i] - 1]]++] = sa[i] - 1;\
}\
memcpy(x, c, sizeof(int) * z);\
for (i = n - 1; i >= 0; --i) {\
if (sa[i] && t[sa[i] - 1]) sa[--x[s[sa[i] - 1]]] = sa[i] - 1;\
}\
}
void sais(int *s, int *sa, int *p, bool *t, int *c, int n, int z) {
bool neq = t[n - 1] = 1;
int nn = 0, nmxz = -1, *q = sa + n, *ns = s + n, *x = c + z, lst = -1, i, j;
memset(c, 0, sizeof(int) * z);
for (i = 0; i < n; ++i) ++c[s[i]];
for (i = 0; i < z - 1; ++i) c[i + 1] += c[i];
for (i = n - 2; i >= 0; i--) t[i] = (s[i] == s[i + 1] ? t[i + 1] : s[i] < s[i + 1]);
MAGIC(
for (i = 1; i < n; ++i) {
if (t[i] && !t[i - 1]) sa[--x[s[i]]] = p[q[i] = nn++] = i;
}
);
for (i = 0; i < n; ++i) if((j = sa[i]) && t[j] && !t[j - 1]) {
neq = lst < 0 || memcmp(s + j, s + lst, (p[q[j] + 1] - j) * sizeof(int));
ns[q[lst = j]] = nmxz += neq;
}
if (nmxz == nn - 1) for (i = 0; i < nn; ++i) q[ns[i]] = i;
else sais(ns, q, p + nn, t + n, c + z, nn, nmxz + 1);
MAGIC(
for (i = nn - 1; i >= 0; --i) sa[--x[s[p[q[i]]]]] = p[q[i]];
);
}
#undef MAGIC
static const int MXN = 500000;
int s[MXN * 2 + 5], sa[MXN * 2 + 5], p[MXN + 5], c[MXN * 2 + 5];
bool t[MXN * 2 + 5];
signed main() {
int n = 0;
while ((s[n] = getchar()) != '\n')
++n;
s[n++] = 0;
sais(s, sa, p, t, c, n, 256);
for (int i = 0; i < n; i++)
if (sa[i] + 1 != n)
printf("%d ", sa[i]);
}
洛谷 P2408
题意
给定一个回文串,求出不同的子串的个数。
思路
做法1:
首先,我们先得知道一件事情:所有子串都是一个后缀的前缀。
然后,我们还是看到 banana 这个例子上:
我们把它的后缀排好序之后就是:
a
ana
anana
banana
na
nana
我们可以发现,对于每一个后缀,如果它的某些前缀不能选,那么一定是在上一个后缀中出现过。
我们定义 \(h_i = lcp(s_i, s_{i - 1}) \ (lcp 表示最长公共前缀)\)
所以我们可以先求出后缀数组,然后直接二分 + 哈希求出每一个 \(h_i\),算出答案。
做法2:
\(lcp(s[sa[rnk[i - 1] - 1]], s[i - 1])\) 最短等于 \(lcp(s[sa[rnk[i] - 1]], s[i]) - 1\)。
证明如下:

所以,我们求出后缀数组后,直接从最长的后缀开始依次计算 \(h_i\),时间复杂度为 \(O(n)\)。
复杂度瓶颈在于求后缀数组上。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, h[N], rnk[N], sa[N];
string s;
pair<int, int> temp[N];
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> s;
long long ans = 1ll * n * (n + 1) / 2;
for (int i = 0; i < n; i++) rnk[i] = s[i], sa[i] = i;
for (int t = 1; t < n; t *= 2) {
for (int i = 0; i < n; i++) temp[i] = {rnk[i], i + t < n ? rnk[i + t] : -1};
sort(sa, sa + n, [](int i, int j) {return temp[i] < temp[j];});
for (int i = 0; i < n; i++) {
if (i > 0 && temp[sa[i]] == temp[sa[i - 1]]) rnk[sa[i]] = rnk[sa[i - 1]];
else rnk[sa[i]] = i;
}
}
for (int i = 0, len = 0; i < n; i++) {
if (!rnk[i]) continue;
while (max(i, sa[rnk[i] - 1]) + len < n && s[i + len] == s[sa[rnk[i] - 1] + len]) len++;
ans -= len, len = max(0, len - 1);
}
cout << ans << '\n';
return 0;
}
洛谷 P5353
题意
给定一棵树,每个结点上有一个字母,一个结点所代表的字符串是从当前结点到根结点的路径上的字符组成的字符串。
请你给这些字符串按照字典序排序,如果两个串完全一样,就比较他们父亲的排名,否则比较自己编号。
思路
这个本质上就是求出后缀数组,但是,我们的两个关键字是往父亲找的。
也就是说,先预处理出 \(2 ^ i\) 级祖先,然后直接用即可。
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
int n, fa[N][20], dfn[N], cnt;
string s;
vector<int> g[N];
int rnk[N], sa[N];
pair<int, int> temp[N];
void dfs(int u) {
dfn[u] = ++cnt;
for (int v : g[u]) dfs(v);
}
void P() {
for (int i = 1; i < 20; i++) {
for (int j = 1; j <= n; j++) fa[j][i] = fa[fa[j][i - 1]][i - 1];
}
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
for (int i = 2; i <= n; i++) cin >> fa[i][0], g[fa[i][0]].push_back(i);
cin >> s, s = ' ' + s;
dfs(1), P();
for (int i = 1; i <= n; i++) rnk[i] = s[i], sa[i] = i;
for (int t = 0; (1 << t) < n; t++) {
for (int i = 1; i <= n; i++) temp[i] = {rnk[i], fa[i][t] ? rnk[fa[i][t]] : -1};
sort(sa + 1, sa + n + 1, [](int i, int j) {return temp[i] == temp[j] ? dfn[i] < dfn[j] : temp[i] < temp[j];});
for (int i = 1; i <= n; i++) {
if (i > 0 && temp[sa[i]] == temp[sa[i - 1]]) rnk[sa[i]] = rnk[sa[i - 1]];
else rnk[sa[i]] = i;
}
}
for (int i = 1; i <= n; i++) cout << sa[i] << ' ';
return 0;
}
loj 103
题意
给定字符串 \(A, B\),求出 \(B\) 在 \(A\) 中出现的次数。
思路
由于后缀数组是按照字典序排序后得到的,所以可以发现,如果我们要查找一个字符串 \(B\),那么他作为某个后缀的前缀出现时,那些后缀在后缀数组上必定是一段连续的区间。
我们还是看到 banana 这个例子,我们已经知道,它的后缀排序后是:
a
ana
anana
banana
na
nana
如果我们要查找 a 这个字符串出现了多少次,可以发现,它作为某个后缀的前缀出现时,对应的区间是 \([1, 3]\)
所以,我们可以二分查找字符串 \(B\) 对应的左端点和右端点。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
string s, t;
int n, m, rnk[N], sa[N], cnt[N], a[N];
pair<int, int> temp[N];
bool Check_left(int x) {
for (int i = 0; i < min(m, n - sa[x]); i++) if (s[sa[x] + i] != t[i]) return s[sa[x] + i] > t[i];
return (n - sa[x] < m) ? 0 : 1;
}
bool Check_right(int x) {
for (int i = 0; i < min(m, n - sa[x]); i++) if (s[sa[x] + i] != t[i]) return s[sa[x] + i] < t[i];
return 1;
}
int Find_left() {
int l = 0, r = n - 1;
while (l < r) {
int mid = (l + r) >> 1;
Check_left(mid) ? r = mid : l = mid + 1;
}
return l;
}
int Find_right() {
int l = 0, r = n - 1;
while (l < r) {
int mid = (l + r + 1) >> 1;
Check_right(mid) ? l = mid : r = mid - 1;
}
return l;
}
void Sort() {
for (int i = 0; i < n; i++) cnt[temp[i].second]++;
for (int i = 1; i < N; i++) cnt[i] += cnt[i - 1];
for (int i = n - 1; i >= 0; i--) a[--cnt[temp[sa[i]].second]] = sa[i];
fill(cnt, cnt + N, 0);
for (int i = 0; i < n; i++) cnt[temp[i].first]++;
for (int i = 1; i < N; i++) cnt[i] += cnt[i - 1];
for (int i = n - 1; i >= 0; i--) sa[--cnt[temp[a[i]].first]] = a[i];
fill(cnt, cnt + N, 0);
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> s >> t, n = s.size(), m = t.size();
for (int i = 0; i < n; i++) rnk[i] = s[i], sa[i] = i;
for (int t = 1; t < n; t *= 2) {
for (int i = 0; i < n; i++) temp[i] = {rnk[i], i + t < n ? rnk[i + t] : 0};
Sort();
for (int i = 0; i < n; i++) {
if (i > 0 && temp[sa[i]] == temp[sa[i - 1]]) rnk[sa[i]] = rnk[sa[i - 1]];
else rnk[sa[i]] = i + 1;
}
}
cout << Find_right() - Find_left() + 1;
return 0;
}
loj 2033
题意
给定一个长度为 \(n\) 的数组 \(a\),有 \(n\) 次操作,第 \(i\) 次操作将 \(a_i\) 插入字符串末尾,请你求出每一次操作后字符串中不同的子串的数量。
思路
首先,我们考虑加入一个字符会造成什么改变。
不难发现,加入一个字符会使得所有后缀都需要添加一个字符,并且还要多一个后缀。
所以我们考虑将字符串倒过来,也就是说,每次添加字符只会多一个后缀,其他后缀不会受到影响。
在上面我们已经说过,在求不同子串数量时,我们有 \(h_i = lcp(s_i, s_{i - 1})\)。
根据一些例子,我们可以发现,\(lcp(s_i, s_j) = min\{lcp(s_i, s_{i + 1}), \dots, lcp(s_{j - 1}, s_j)\}\)。
也就是说,我们可以预处理出所有的 \(h_i\)了,在每次加入字符时,二分查找出距离当前后缀对应编号最近的两个后缀,分别求出区间最小值,加上贡献。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5 + 10;
int n, x[N], rnk[N], sa[N], c[N], tr[4 * N], h[N];
ll ans;
pair<int, int> temp[N];
set<int> s;
int Make_Tree(int i, int l, int r) {
if (l == r) return tr[i] = h[l];
int mid = (l + r) >> 1;
return tr[i] = min(Make_Tree(i * 2, l, mid), Make_Tree(i * 2 + 1, mid + 1, r));
}
int query(int i, int l, int r, int ql, int qr) {
if (qr < l || ql > r) return 1e9;
if (ql <= l && r <= qr) return tr[i];
int mid = (l + r) >> 1;
return min(query(i * 2, l, mid, ql, qr), query(i * 2 + 1, mid + 1, r, ql, qr));
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
for (int i = 0; i < n; i++) cin >> x[i];
reverse(x, x + n);
for (int i = 0; i < n; i++) rnk[i] = x[i], sa[i] = i;
for (int t = 1; t < n; t *= 2) {
for (int i = 0; i < n; i++) temp[i] = {rnk[i], i + t < n ? rnk[i + t] : -1};
sort(sa, sa + n, [](int i, int j) {return temp[i] < temp[j];});
for (int i = 0; i < n; i++) {
if (i > 0 && temp[sa[i]] == temp[sa[i - 1]]) rnk[sa[i]] = rnk[sa[i - 1]];
else rnk[sa[i]] = i;
}
}
for (int i = 0; i < n; i++) c[n - sa[i] - 1] = i;
for (int i = 0, len = 0; i < n; i++) {
if (!rnk[i]) continue;
while (max(i, sa[rnk[i] - 1]) + len < n && x[i + len] == x[sa[rnk[i] - 1] + len]) len++;
h[rnk[i] - 1] = len, len = max(0, len - 1);
}
Make_Tree(1, 0, n - 2);
for (int i = 0; i < n; i++) {
int res = 0;
auto it = s.lower_bound(c[i]);
if (it != s.begin()) res = max(res, query(1, 0, n - 2, *prev(it), c[i] - 1));
if (it != s.end()) res = max(res, query(1, 0, n - 2, c[i], *it - 1));
ans += res;
cout << 1ll * (i + 1) * (i + 2) / 2 - ans << '\n';
s.insert(c[i]);
}
return 0;
}
洛谷 P3804
题意
给定一个字符串 \(s\),求出 \(s\) 中所有出现次数不为 \(1\) 的子串的出现次数乘上该子串的长度的最大值。
思路
不难发现,在求出后缀数组后,我们一定会选择相邻两串的最长公共前缀作为这次考虑的子串。
我们又在之前说过,一个子串作为某个后缀的前缀出现所对应的后缀一定是一段区间,也就是说,我们枚举每一个最长公共前缀,二分求出它所对应的区间,求答案即可。
在这里,求区间有两种做法,第一种是算出 \(h\) 值后,直接比较,也就是说求出 \(h_i\) 两边第一个比它小的值的位置,这种做法可以二分也可以单调栈,第二种就是直接哈希判断是否相等。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e6 + 10;
int n, rnk[N], sa[N], h[N], l[N], r[N], top, stk[N];
ll ans;
string s;
pair<int, int> temp[N];
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> s, n = s.size();
for (int i = 0; i < n; i++) rnk[i] = s[i], sa[i] = i;
for (int t = 1; t < n; t *= 2) {
for (int i = 0; i < n; i++) temp[i] = {rnk[i], i + t < n ? rnk[i + t] : -1};
sort(sa, sa + n, [](int i, int j) {return temp[i] < temp[j];});
for (int i = 0; i < n; i++) {
if (i > 0 && temp[sa[i]] == temp[sa[i - 1]]) rnk[sa[i]] = rnk[sa[i - 1]];
else rnk[sa[i]] = i;
}
}
for (int i = 0, len = 0; i < n; i++) {
if (!rnk[i]) continue;
while (max(i, sa[rnk[i] - 1]) + len < n && s[i + len] == s[sa[rnk[i] - 1] + len]) len++;
h[rnk[i] - 1] = len, len = max(0, len - 1);
}
stk[0] = -1;
for (int i = 0; i < n - 1; i++) {
while (top && h[stk[top]] >= h[i]) r[stk[top--]] = i;
l[i] = stk[top], stk[++top] = i;
}
while (top) r[stk[top--]] = n - 1;
for (int i = 0; i < n - 1; i++) ans = max(ans, 1ll * h[i] * (r[i] - l[i]));
cout << ans;
return 0;
}
回文树
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int n, tr[N][26], nxt[N], len[N], c = 1;
string s;
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> s, n = s.size(), s = ' ' + s;
// 回文树的奇根为 0,偶根为 1
len[0] = -1, nxt[0] = 0, len[1] = 0, nxt[1] = 0;
for (int i = 1, j = 1 /*j 是 i - 1 的后缀的最长回文后缀对应回文树上的结点编号*/; i <= n; i++) {
while (s[i] != s[i - len[j] - 1]) j = nxt[j];
if (!tr[j][s[i] - 'a']) {
tr[j][s[i] - 'a'] = ++c, len[c] = len[j] + 2;
for (int &k = nxt[c] = nxt[j]; s[i] != s[i - len[k] - 1]; k = nxt[k]);
if (len[c] > 1) nxt[c] = tr[nxt[c]][s[i] - 'a'];
else nxt[c] = 1;
}
j = tr[j][s[i] - 'a'];
}
return 0;
}



