P1983 题解
P1983 [NOIP2013 普及组] 车站分级
题意
在一条单向的铁路上,依次有 \(n\) 个编号为 \(1, 2, 3, \dots n\) 火车站,每个火车站都有一个级别,最低为 \(1\) 级。
现在,有若干趟车次在这条铁路上行驶,每一趟都满足以下要求:如果这趟车次经过了车站 \(x\),那么在起始站到终点站之间的所有级别大于等于车站 \(x\) 的级别的车站都需要停靠。
现在给出 \(m\) 趟车次的运行情况(都满足要求),请你求出最少要给这条铁路上的车站分几个级别。
\(1 \le n, m \le 1000\)
思路
首先,通过题目,我们可以得到一个信息:
对于起点为 \(st\),终点为 \(en\) 的一趟车次来说,\(st \sim en\) 中的所有没有停靠的车站的级别一定都要小于停靠的车站的级别。
比如说,设第 \(i\) 个车站的级别为 \(l_i\),如果这趟车次停靠了 1 3 4 5,那么说明 \(l_2 < l_1, l_2 < l_3, l_2 < l_4, l_2 < l_5\),如果不是这样的话,那么第 \(2\) 个车站就会被停靠了。
所以,我们可以将 \(<\) 看作为一条有向边,将每个车站看作一个点。当 \(l_u < l_v\) 时,图上有一条 \(u\) 到 \(v\) 的有向边。
那么,我们就可以发现,因为要求分的级别最小,所以入度为 \(0\) 的点的级别一定为 \(1\)。
也就是说,每条边的边权都为 \(1\),而我们又知道某些点的级别,所以就是将所有的点的最小级别求出来后,求最大值即可。
那么这个题目就变成了求最长路(洛谷 P1807)了!!!
因为这个级别虽然要求的是最小的,但是它也必须满足所有的点,所以是最长路。
那我们来回忆一下,最长路应该怎么做呢?
其实很简单,设 \(1\) 到 \(i\) 的最短路为 \(s_i\),很显然,有这么一个递推公式:
为了能够求出 \(s_i\),我们必须先求出所有的 \(s_j\),所以这里又对应到了一个算法,拓扑排序!!!
那么事情就好办了,
-
建图
-
求出拓扑序(拓扑排序)
-
递推求解
-
统计答案
但是……事情真的有这么简单吗?
我们来算一下时间复杂度:
- 建图:对于每一趟车次来说,最多有 \(n ^ 2\) 条边要连,总共有 \(m\) 趟车次,所以时间复杂度为 \(O(n ^ 2 \times m)\)
而看一眼数据范围,非常好,\(1 \le n, m \le 1000\),绝对会超时(但是不知道为什么,就是过了?)
那么,我们应该怎么优化时间复杂度呢?
这其实就涉及到一个建图的小技巧了,先看到这样一张图:
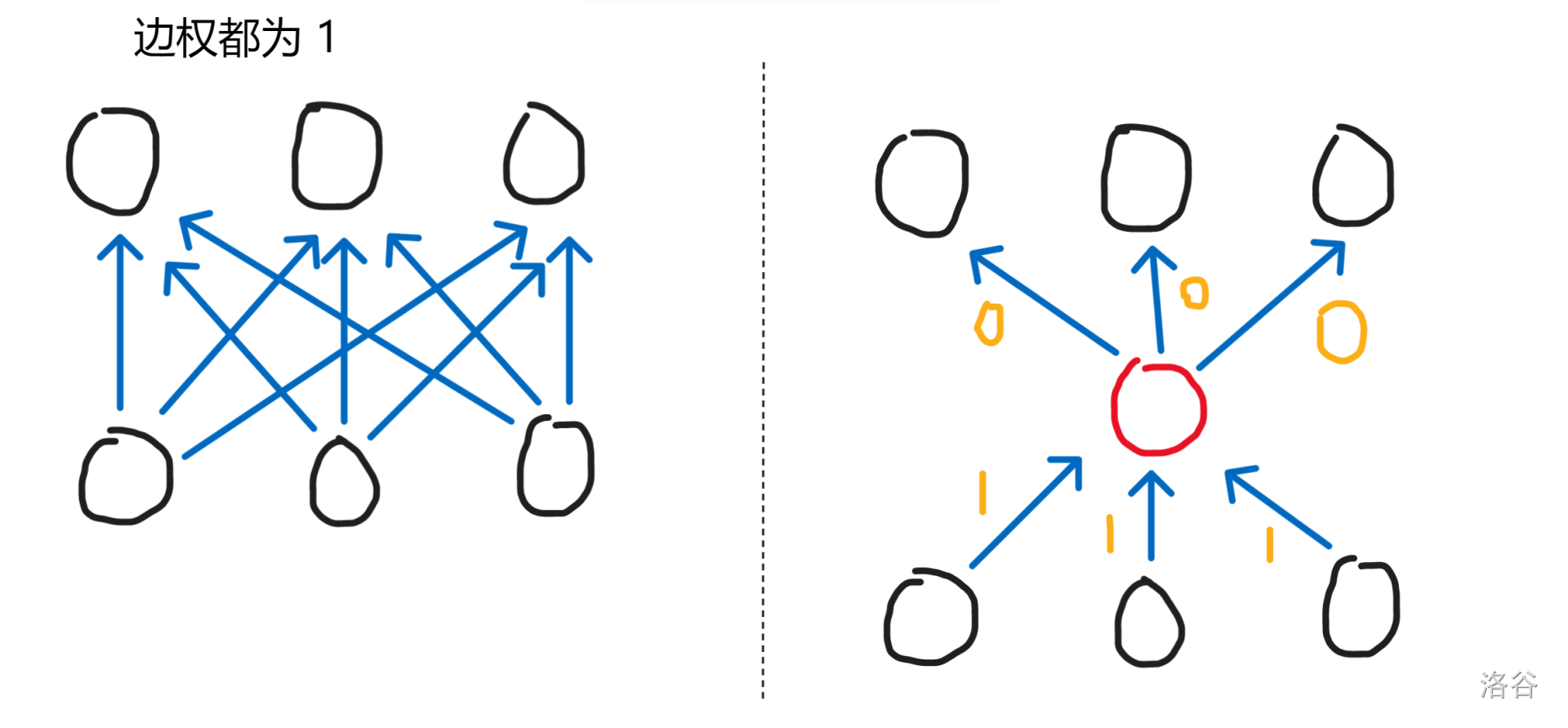
也就是再多建立一个虚拟点去建图(注意,这里要记录边权!!!),这样,就只需要连 \(n\) 条边了,时间复杂度就降到了 \(O(n \times m)\)。
所以,最终的时间复杂度为 \(O(n \times m)\):
-
建图:上面已经讲过了,\(O(n \times m)\)。
-
求拓扑序(拓扑排序):状态数为 \(n + m\),转移数为 \(n \times m\),时间复杂度为 \(O(n \times m)\)。
-
递推求解:可以直接在拓扑排序时求解。
-
统计答案:遍历所有点,\(O(n)\)。
总时间复杂度为 \(O(n \times m)\)。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1010, M = 1010;
int n, m, s[N + M], l[N + M], ans, c[N];
bool f[N];
struct Node {
int v, w; // 连接出去的点,边权
};
vector<Node> g[N + M];
queue<int> que;
// 拓扑排序
void bfs() {
for (int i = 1; i <= n + m; i++) {
if (!s[i]) {
que.push(i), l[i] = 1;
}
}
while (!que.empty()) {
int u = que.front();
que.pop();
for (auto v : g[u]) {
s[v.v]--, l[v.v] = max(l[v.v], l[u] + v.w); // 求解
if (!s[v.v]) {
que.push(v.v);
}
}
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int p;
cin >> p;
fill(f + 1, f + n + 1, 0);
for (int j = 1; j <= p; j++) {
cin >> c[j];
// 建图
g[i + n].push_back({c[j], 0});
f[c[j]] = 1, s[c[j]]++;
}
for (int j = c[1]; j <= c[p]; j++) {
if (!f[j]) {
// 建图
g[j].push_back({i + n, 1});
s[i + n]++;
}
}
}
bfs();
for (int i = 1; i <= n; i++) {
ans = max(ans, l[i]); // 求解
}
cout << ans;
return 0;
}



