图论
图的相关定义
图有很多种,有向图(只有有向边的图),无向图(只有无向边的图),混合图(既有无向边,也有有向边的图)等。
度数
在无向图中,点 \(i\) 的度数就是从 \(i\) 连出去的边的数量。
在有向图中,点 \(i\) 的度数分为入度和出度。
入度指的是从其它点 \(j\) 连向 \(i\) 的边的数量。
出度指的是从点 \(i\) 连出去的边的数量。
简单图
自环:如果存在一条 \(i\) 连到 \(i\) 的边,则说明存在自环。
重边:如果边集存在两条边 \((u_i, v_i)\) 和 \((u_j, v_j)\),且 \(u_i = u_j, v_i = v_j\),则说明存在重边。
简单图就是指不存在自环和重边的图。
如果图中存在自环或重边,这个图就被称为多重图。
反图
对于一个有向图 \(G\) 来说,它的反图指所有 \(u\) 到 \(v\) 的边都变成 \(v\) 到 \(u\) 的边的图。
特殊的图
完全图:若无向简单图 \(G\) 满足任意两点之间都有边,\(G\) 就是完全图。
有向完全图:若有向图 \(G\) 满足任意两点之间都有两条不同方向的边,\(G\) 就是有向完全图。
图的存储
邻接矩阵
直接用 g[i][j] 来表示有没有一条 \(i\) 到 \(j\) 的边,或是存储边权。
适用于:\(n \le 1000\),稠密图。
空间复杂度为 \(O(n ^ 2)\)。
邻接表
用 vector 存储每个点连出去每一条边。
适用于:\(n \le 10 ^ 5, m \le 10 ^ 6\),稀疏图。
空间复杂度为 \(O(n + m)\)。
链式前向星
用链表存储所有边,也就是说,记录每个点 \(i\) 连出去的第一条边的编号 \(head_i\) 和最后一条边的编号 \(tail_i\),每次加边时,就往 \(tail_i\) 后加上一条边,同时更新 \(tail_i\)。
遍历 \(i\) 连出去的所有边就像遍历一个链表一样,从 \(head_i\) 出发,一直遍历到 \(tail_i\)。
注意:存储边的数组空间要开两倍(\(u\) 到 \(v\) 一条,\(v\) 到 \(u\) 一条)!!!
空间复杂度为 \(O(m + n)\).
拓扑排序
拓扑序
拓扑序列是顶点活动网中将活动按发生的先后次序进行的一种排列。
拓扑排序
拓扑排序就是一种寻找拓扑序的排序。
但必须满足一个要求:这个图是一个有向无环图。
也就是说,如果点 \(u\) 到点 \(v\) 有一条有向边,则在拓扑排序中,\(u\) 得排在 \(v\) 前面。
算法思路
首先,拓扑排序中,排在最前面的点一定是一个入度为 \(0\) 的结点,因为它不是任何一条有向边的终点。
因为这个点已经进入序列了,所以它连出去的所有点又少了一条边要解决,可以理解为当所有边都被解决后,这个点就可以进入序列了。
所以,直接模拟即可。
算法流程
-
不断重复以下步骤,直到容器为空:
-
将图中所有入度为 \(0\) 的点加入容器。
-
取出容器中任意一个元素。
-
断掉这个元素连出去的所有有向边。
-
-
输出拓扑序
void topo_sort() {
for (int i = 1; i <= n; i++) {
if (!deg[i]) que.push(i);
}
while (!que.empty()) {
int tmp = que.front();
que.pop();
for (auto v : g[tmp]) {
deg[v.v]--;
if (!s[v.v]) que.push(v.v);
}
}
}
欧拉路
定义
-
欧拉回路:通过图中每条边恰好一次的回路(类似于一个一笔画问题)
-
欧拉通路:通过图中每条边恰好一次的通路
-
欧拉图:具有欧拉回路的图
-
半欧拉图:具有欧拉通路但不具有欧拉回路的图
欧拉路和欧拉回路的存在性判断
首先,我们需要用 DFS 或者并查集判连通性。
-
无向图的判断条件:如果所有的点都是偶点,则存在欧拉回路,任何点都可以作为起点和终点。如果只有两个奇点,则存在欧拉路,其中一个奇点是起点,另一个是终点。
-
有向图的判断条件:把一个点的出度记为 \(1\),入度记为 \(-1\),那么这个点的入度加出度就是它的度数。如果所有点的度数都是 \(0\),那么存在欧拉路。如果只有一个度数为 \(1\) 的点,一个度数为 \(-1\) 的点,并且其他点的度数都是 \(0\),那么存在欧拉路,其中,度数为 \(1\) 的是起点,度数为 \(-1\) 的是终点。
输出一个欧拉回路
对一个无向连通图做 dfs,就输出了一个欧拉回路。
代码输出的路径,实际上是从终点到起点的一条路径。对于无向图,因为起点和终点都是一个点,所以并没有关系。
如果是有向图,输出的就是一条逆向的路径,我们只需要用栈存下这条路径,再输出正序即可。
void dfs(int t, int fa) {
p.push_back(t);
bool flag = 0;
for (pii i : g[t]) {
if (!f[i.second] && i.first != fa) {
f[i.second] = 1, flag = 1;
dfs(i.first, t);
}
}
p.push_back(fa);
}
最小生成树
Kruskal 算法
贪心 + 并查集。
我们既然是想要生成树上的边权值和最小,肯定尽量选择边权小的边。
所以,我们先将所有的边按照权值从小到大排序。
然后,对于每一条边 \((u, v, w)\),如果 \(u, v\) 不联通,这条边就可以加入到最小生成树上。
连通性就可以用并查集来判断。
struct Edge {
int u, v, w;
bool operator < (const Edge &i) const {
return w < i.w;
}
} a[M];
int Find(int t) {
return fa[t] ? fa[t] = Find(fa[t]) : t;
}
int main() {
ios::sync_with_stdio(0),cout.tie(0);
cin >> n >> m;
for (int i = 1; i <= m; i++) {
cin >> a[i].u >> a[i].v >> a[i].w;
}
sort(a + 1, a + m + 1);
for (int i = 1; i <= m; i++) {
int u = Find(a[i].u), v = Find(a[i].v);
if (u != v) fa[u] = v, ans += a[i].w;
}
cout << ans;
return 0;
}
Prim 算法
Prim 和 Kruskal 的区别在于,Kruskal 是加边,Prim 是加点。
具体来说,每次要选择距离最小的一个结点,以及用新的边更新其他结点的距离。
其实跟 Dijkstra 算法一样,每次找到距离最小的一个点,可以暴力找也可以用堆维护。
暴力:\(O(n ^ 2 + m)\),二叉堆:\(O((n + m) \log n)\)。
struct Edge {
int u, v, w;
bool operator < (const Edge &i) const {
return w > i.w;
}
};
vector<pair<int, int>> g[N];
priority_queue<Edge> que;
void prim() {
int ans = 0, c = 1;
con[1] = 1;
for (auto [v, w] : g[1]) {
que.push({1, v, w});
}
while (c < n) {
while (!que.empty() && con[que.top().u] == con[que.top().v]) {
que.pop();
}
auto [u, v, w] = que.top();
que.pop(), ans += w;
if (con[u]) swap(u, v);
con[u] = 1, c++;
for (auto [x, y] : g[u]) {
que.push({u, x, y});
}
}
cout << ans;
}
次小生成树
非严格次小生成树
我们可以先用 Kruskal 算法建出最小生成树,然后对于每一条非树边 \((u, v, w)\),我们把 \(u\) 到 \(v\) 的路径上的最小值找出来,用 \(w\) 替换掉这个最小值,就得到了另一颗生成树,最后将所有重新得到的生成树的边权之和取最小值即可。
但是,我们应该怎么快速的求出 \(u\) 到 \(v\) 的路径上的最小边权呢?
我们可以用倍增维护 \(i\) 到 \(i\) 的第 \(2 ^ j\) 级祖先所经过的边权的最小值,然后对于 \(u, v\),边求 \(lca\),边求最小值。
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int M = 5010, N = 110;
int T, n, m, s, fa[N];
int dep[N], ffa[N][10], mmax[N][10];
bool f[M], flag;
struct Edge {
int u, v, w;
bool operator < (const Edge &i) const {
return w < i.w;
}
} e[M];
struct Node {
int v, w;
};
vector<Node> g[N];
int Find(int t) {
if (fa[t]) return fa[t] = Find(fa[t]);
else return t;
}
void dfs(int t, int fa) {
ffa[t][0] = fa, dep[t] = dep[fa] + 1;
for (int i = 0; i < g[t].size(); i++) {
if (g[t][i].v != fa) mmax[g[t][i].v][0] = g[t][i].w, dfs(g[t][i].v, t);
}
}
void P() {
for (int i = 1; i < 10; i++) {
for (int j = 1; j <= n; j++) {
ffa[j][i] = ffa[ffa[j][i - 1]][i - 1];
mmax[j][i] = max(mmax[j][i - 1], mmax[ffa[j][i - 1]][i - 1]);
}
}
}
int Maxw_on_LCA(int x, int y) {
if (dep[x] < dep[y]) swap(x, y);
int d = dep[x] - dep[y], maxw = 0;
for (int i = 9; i >= 0; i--) {
if (d & (1 << i)) {
maxw = max(maxw, mmax[x][i]);
x = ffa[x][i];
}
}
for (int i = 9; i >= 0; i--) {
if (ffa[x][i] != ffa[y][i]) {
maxw = max(maxw, max(mmax[x][i], mmax[y][i]));
x = ffa[x][i], y = ffa[y][i];
}
}
return maxw;
}
void Solve() {
cin >> n >> m;
for (int i = 1; i <= m; i++) {
cin >> e[i].u >> e[i].v >> e[i].w;
}
sort(e + 1, e + m + 1);
for (int i = 1; i <= m; i++) {
int u = Find(e[i].u), v = Find(e[i].v);
if (u != v) {
fa[u] = v, f[i] = 1, s += e[i].w;
g[e[i].u].push_back({e[i].v, e[i].w});
g[e[i].v].push_back({e[i].u, e[i].w});
}
}
dfs(1, 0), P();
for (int i = 1; i <= m; i++) {
if (!f[i]) {
int tmp = Maxw_on_LCA(e[i].u, e[i].v);
flag |= tmp == e[i].w;
}
f[i] = 0;
}
if (flag) cout << "Not Unique!\n";
else cout << s << '\n';
s = flag = 0;
for (int i = 1; i <= n; i++) {
g[i].clear(), fa[i] = dep[i] = 0;
for (int j = 0; j < 10; j++) {
mmax[i][j] = ffa[i][j] = 0;
}
}
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> T;
while (T--) Solve();
return 0;
}
严格次小生成树
其实严格次小生成树和次小生成树的区别就在于我们不只要维护最小值,还要维护次小值。
void P() {
for (int i = 1; i < 20; i++) {
for (int j = 1; j <= n; j++) {
ffa[j][i] = ffa[ffa[j][i - 1]][i - 1];
fir[j][i] = max(fir[j][i - 1], fir[ffa[j][i - 1]][i - 1]);
if (fir[j][i - 1] == fir[ffa[j][i - 1]][i - 1]) {
sec[j][i] = max(sec[j][i - 1], sec[ffa[j][i - 1]][i - 1]);
} else {
sec[j][i] = min(fir[j][i - 1], fir[ffa[j][i - 1]][i - 1]);
}
}
}
}
pair<int, int> Maxw_on_LCA(int x, int y) {
if (dep[x] < dep[y]) swap(x, y);
int d = dep[x] - dep[y];
int firw = 0, secw = 0;
for (int i = 19; i >= 0; i--) {
if (d & (1 << i)) {
if (firw < fir[x][i]) {
secw = max(firw, sec[x][i]);
firw = fir[x][i];
} else if (firw > fir[x][i]) {
secw = max(secw, fir[x][i]);
} else if (firw == fir[x][i]) {
secw = max(secw, sec[x][i]);
}
x = ffa[x][i];
}
}
if (x == y) return {firw, secw};
for (int i = 19; i >= 0; i--) {
if (ffa[x][i] != ffa[y][i]) {
if (firw < fir[x][i]) {
secw = max(firw, sec[x][i]);
firw = fir[x][i];
} else if (firw > fir[x][i]) {
secw = max(secw, fir[x][i]);
} else if (firw == fir[x][i]) {
secw = max(secw, sec[x][i]);
}
if (firw < fir[y][i]) {
secw = max(firw, sec[y][i]);
firw = fir[y][i];
} else if (firw > fir[y][i]) {
secw = max(secw, fir[y][i]);
} else if (firw == fir[y][i]) {
secw = max(secw, sec[y][i]);
}
x = ffa[x][i], y = ffa[y][i];
}
}
if (firw < fir[x][0]) {
secw = max(firw, sec[x][0]);
firw = fir[x][0];
} else if (firw > fir[x][0]) {
secw = max(secw, fir[x][0]);
} else if (firw == fir[x][0]) {
secw = max(secw, sec[x][0]);
}
if (firw < fir[y][0]) {
secw = max(firw, sec[y][0]);
firw = fir[y][0];
} else if (firw > fir[y][0]) {
secw = max(secw, fir[y][0]);
} else if (firw == fir[y][0]) {
secw = max(secw, sec[y][0]);
}
return {firw, secw};
}
连通性相关
强连通分量
Tarjan 算法
在 Tarjan 算法中为每个结点 \(u\) 维护了以下变量。
-
\(dfn_u\):在
dfs时 \(u\) 被搜索的次序。 -
\(low_u\):在 \(u\) 的子树中能够回溯到的最早的在栈中的结点。
一个结点的子树内的结点的 \(dfn\) 都严格大于当前点的 \(dfn\)。
从根开始的一条路径上的 \(dfn\) 严格递增,\(low\) 严格非降。
我们按照 dfs 的次序对图中所有节点进行搜索,维护每个点的 \(dfn\) 和 \(low\),并且将搜索到的结点入栈。每找到一个强连通分量,就让相对应的元素出栈。
在搜索过程中,对于结点 \(u\) 和它相邻的结点 \(v\) 考虑 \(3\) 种情况:
-
\(v\) 没有被访问过:对 \(v\) 进行
dfs。在回溯时,用 \(low_v\) 更新 \(low_u\)。 -
\(v\) 被访问过,且在栈中:用 \(dfn_v\) 更新 \(low_u\)。
-
\(v\) 被访问过,不在栈中:说明 \(v\) 所在的强连通分量已经处理完毕,不用对其进行操作。
在一个连通分量图内,有且仅有一个点 \(u\) 使得 \(dfn_u = low_u\)。该结点一定是在深度遍历的过程中,该连通分量中第一个被访问过的结点,因为它的 \(dfn\) 和 \(low\) 值最小,不会被该连通分量中的其他结点所影响。
所以,在回溯的过程中,我们判断 \(dfn_u = low_u\) 是否成立,如果成立,则栈中 \(u\) 及上方的结点构成一个强连通分量。
int dfn[N], low[N], tot, top, stk[N], cnt, scc[N];
bool f[N];
void Tarjan(int u) {
dfn[u] = low[u] = ++tot;
f[u] = 1, stk[++top] = u;
for (int v : g[u]) {
if (!dfn[v]) Tarjan(v), low[u] = min(low[u], low[v]);
else if (f[v]) low[u] = min(low[u], dfn[v]);
}
if (dfn[u] == low[u]) {
cnt++;
while (1) {
int tmp = stk[top--];
scc[tmp] = cnt, f[tmp] = 0;
if (u == tmp) break;
}
}
}
割点和桥
割点
对于一个无向图,如果把一个点删除后这个图的极大连通分量数增加了,那么这个点就是这个图的割点(又称割顶)。
过程
如果我们尝试删除每个点,并且判断这个图的连通性,那么复杂度会特别的高。所以,我们需要使用一个常用的算法:Tarjan。
首先,我们看到这个图:
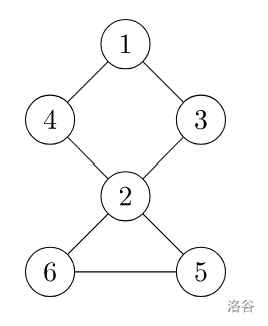
不难看出,这张图中的割点是 \(2\),而且有且仅有这一个割点。
我们直接按照 Tarjan 的步骤进行 dfs 即可,我们判断某个点是否是割点的根据是:对于某个顶点 \(u\),如果存在至少一个顶点 \(v\)(\(u\) 的儿子),使得 \(low_v \ge dfn_u\),即不能回到祖先,那么 \(u\) 点为割点。
但是,对于我们 dfs 的起始点,是需要特殊考虑的:如果它不是割点,那么在搜索树中,它只会有一个儿子。所以,当起始点在搜索树中有两个及以上的儿子结点,那么,它就是一个割点。
int dfn[N], low[N], tot;
bool vis[N];
vector<pii> g[N];
void dfs(int u, int f, int rt) {
dfn[u] = low[u] = ++tot;
int c = 0;
for (pii p : g[u]) {
int v = p.first, id = p.second;
if (!dfn[v]) {
c++, dfs(v, id, rt), low[u]= min(low[u], low[v]);
if (low[v] >= dfn[u] && u != rt) ans += !vis[u], vis[u] = 1;
} else if (f != id) low[u] = min(low[u], dfn[v]);
}
if (u == rt && c >= 2) ans++, vis[u] = 1;
}
割边
和割点差不多,叫做桥。
对于一个无向图,如果删掉一条边后图中的连通分量数增加了,则称这条边为桥或者割边。严谨来说,就是:假设有连通图 \(G=\{V,E\}\),\(e\) 是其中一条边(即 \(e \in E\)),如果 \(G-e\) 是不连通的,则边 \(e\) 是图 \(G\) 的一条割边(桥)。
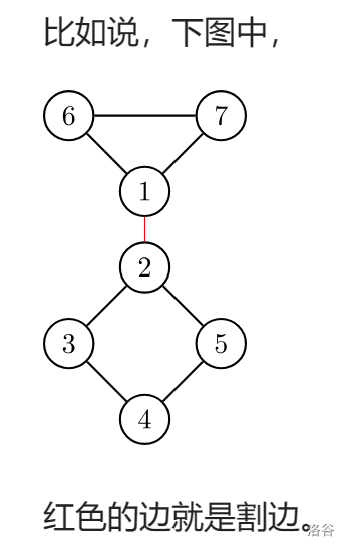
过程
和割点差不多,只要改一处:\(low_v > dfn_u\) 就可以了,而且不需要考虑根节点的问题。
如果 \(low_v = dfn_u\) 表示还可以回到父节点,如果顶点 \(v\) 不能回到祖先也没有另外一条回到父亲的路,那么 \(u - v\) 这条边就是割边。
int dfn[N], low[N], tot;
vector<int> g[N], bridge;
void dfs(int u, int fa) {
dfn[u] = low[u] = ++tot;
bool flag = 0;
for (int v : g[u]) {
if (!dfn[v]) {
c++, dfs(v, u), low[u] = min(low[u], low[v]);
if (low[v] > dfn[u]) flag = 1;
} else if (v != fa) low[u] = min(low[u], dfn[v]);
}
if (flag) bridge.push_back({fa, u});
}
再提供一种写法:
int dfn[N], low[N], tot;
bool vis[N];
vector<pii> g[N];
void dfs(int u, int f) {
dfn[u] = low[u] = ++tot;
for (pii p : g[u]) {
int v = p.first, id = p.second;
if (!dfn[v]) dfs(v, id), low[u]= min(low[u], low[v]);
else if (f != id) low[u] = min(low[u], dfn[v]);
}
if (low[u] == dfn[u] && f) ans++, vis[f] = 1; // f 是桥
}
最短路
Floyd
用来求任意两点之间的最短路,适用于任何图,不能存在负环。
我们定义 \(f_{k, x, y}\) 为只经过 \(1 \sim k\) 时,\(x\) 到 \(y\) 的最短路。
那么就有 \(f_{k, x, y} = min(f_{k - 1, x, y}, f_{k - 1, x, k} + f_{k - 1, k, y})\)。
特别的,\(f_{0, x, y}\) 为 \(x\) 到 \(y\) 的这条边的边权,如果不存在这条边,\(f_{0, x, y} = \infty\)。
时间复杂度为 \(O(n ^ 3)\),空间复杂度为 \(O(n ^ 3)\)。
我们可以发现,每次更新 \(k\) 的状态,都只和 \(k - 1\) 的状态有关,所以,可以考虑省略第一维。
空间复杂度降到 \(O(n ^ 2)\)。
void Floyd() {
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
f[i][j] = min(f[i][j], f[i][k] + f[k][j]);
}
}
}
}
Bellman–Ford
Bellman–Ford 是一种基于松弛操作的最短路算法,可以求出单源最短路(边权可为负数)。
对于一条边 \((u, v, w)\),松弛操作对应以下式子:\(d_v = min(d_v, d_u + w)\)。
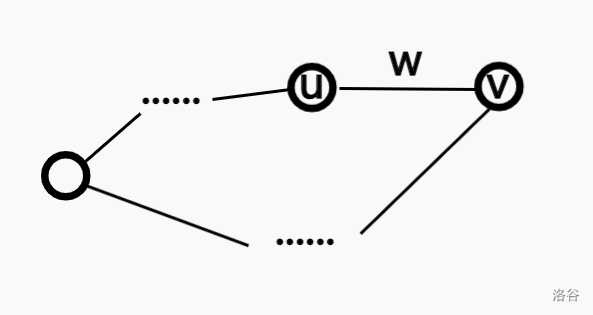
由于从起点到 \(i\) 的最短路最多经过 \(n - 1\) 条边,所以最多进行 \(n - 1\) 次松弛。
时间复杂度为 \(O(nm)\),空间复杂度为 \(O(n)\)。
void Bellman_Ford(int s) {
fill(d + 1, d + n + 1, 1e18), d[s] = 0;
for (int i = 1; i < n; i++) {
for (auto [u, v, w] : e) {
d[v] = min(d[v], d[u] + w);
}
}
}
还有一种情况,如果从 \(S\) 点出发,抵达一个负环时,松弛操作会无休止地进行下去。由于我们只做了 \(n - 1\) 次松弛操作,所以,如果在第 \(n\) 次松弛时,还存在可以松弛的边,就存在从 \(S\) 出发可抵达的负环。
SPFA
SPFA 本质上是 Bellman–Ford 优化后的一种算法。
也就是说,我们考虑每一条边 \((u, v, w)\),如果 \(d_v\) 这次并没有被更新,那么,下一次松弛就没必要考虑从 \(v\) 出发的边了。
所以,我们只要用一个队列来维护在上一轮有哪些点被松弛了,这次只考虑这些点出发的边即可。
void SPFA(int s) {
queue<int> que;
fill(d + 1, d + n + 1, 1e18);
d[s] = 0, que.push(s);
while (!que.empty()) {
int sz = que.size();
for (int j = 1; j <= sz; j++) {
int u = que.front(); que.pop();
for (auto [v, w] : g[u]) {
if (d[v] > d[u] + w) {
d[v] = d[u] + w, que.push(v);
}
}
}
}
}
Dijkstra
Dijkstra 是一种求解非负权图上单源最短路的算法。
本质上就是对边做松弛操作。
也就是说,每次找出最短路长度最小的没有标记的结点 \(u\),并标记,然后对 \(u\) 连出去的所有边做松弛操作。
int Find() {
int ret = 0;
for (int i = 1; i <= n; i++) {
if (d[ret] > d[i] && !vis[i]) ret = i;
}
vis[ret] = 1;
return ret;
}
void Dijkstra(int s) {
fill(d, d + n + 1, 1e18);
d[s] = 0;
for (int i = 1; i <= n; i++) {
int u = Find();
for (auto [v, w] : g[u]) {
d[v] = min(d[v], d[u] + w);
}
}
}
时间复杂度为 \(O(n ^ 2)\)。
其实,我们可以把寻找最短路最小的边的 \(O(n)\) 的循环用优先队列优化掉,也就是说,时间复杂度变成了 \(O(m \log m)\)。
using ll = long long;
struct Node { // 我习惯于把建的边和优先队列中的状态用一个结构体
int v;
ll w;
bool operator < (const Node &i) const {
return w > i.w;
}
};
priority_queue<Node> pq;
vector<Node> g[N];
void Dijkstra(int s) {
fill(d + 1, d + n + 1, 1e18);
d[s] = 0, pq.push(s);
while (!pq.empty()) {
Node u = pq.top(); pq.pop();
if (vis[u.v]) continue;
vis[u.v] = 1;
for (Node v : g[u.v]) {
if (d[v.v] < u.w + v.w) {
d[v.v] = u.w + v.w;
pq.push({v.v, d[v.v]});
}
}
}
}



