最大连续子数列和问题
前言:
第一次接触最大连续子数列和问题是在2008年的夏天,那是在Mark Allen Weiss的data structures and problem solving using C++(数据结构与问题求解(C++版))里看到的。那时由于迷茫,在遇到问题的时候往往毫无头绪,最后只好去网上看一些别人的算法,看了好像也不能理解这个算法为什么这么好,更想知道他们到底是怎么想出来的… 这么多问题纠结在心头,无法解决,也就是从那时开始,开始看一些算法、数据结构的书,渐渐地开始关注数学思想、科学哲学领域的书,也看了网络上刘未鹏的blog,渐渐地开始理清思路…
最大连续子数列和问题就是这一段旅程的起点,就着这一个小问题,我第一次看清了一个问题是怎样从最原始的解法去考虑,慢慢地优化,慢慢地磨,磨到一个远优于原始解法的程度的。这里我看到的是第一步的重要性,跟人生一样,虽然知道第一步很可能而且在很多情况下不是最优的,但是还是要踏下去,踏下去才知道他到底是哪儿不好,应该往什么方向努力,而不是停留在“这个算法可能时间性能不行”的定性的猜测上。在小的问题上多踏实地做做,多走走弯路,才能保证以后在大的问题的决策上你有足够的经验和数据去一步做到较优。
从这个小问题上,以及我后来一年中解决问题的经历中,我都看到了分而治之作为通用的方法论的巨大价值。无论是GOOGLE提出的map-reduce,亦或是所谓的分布式计算、消息传递等等新名词,其本质还是三个单词divide and conquer。其实计算机世界远比人类世界来得简单,不是吗?
好了,我们来看看这道题吧!
问题重述:
给定(可能是负的)整数A1、A2、…、AN,求出(并确定对应的序列) 的最大值。如果所有的整数都是负数,那么最大连续子数列和就是0。
问题分析与求解:
这道题,据Udi Menber在Introduction to Algorithms: a creative approach中的说法,是来自于Bently的名著programming pearls(编程珠玑)。
在讨论这个问题的算法之前,先搞清楚一个问题,那就是:为什么在所有输入都是负数的情况下,最大连续子数列和是0,而不是返回输入中的最大负整数(即绝对值最小的整数)。原因是由整数零组成的空的子数列也是一个子数列,并且其和就是0。该结果与空集是任意集合的子集类似。注意空的情况总是可能出现的,并且在许多例子中它根本不是特殊情况。
最大连续子数列和问题令人感兴趣,主要是因为有如此多的算法用于解决这个问题,并且这些算法的性能相差很大。
好的!废话不多说,我们开始吧:
算法1.暴力搜索
首先想到的当然就是“刀耕火种”的暴力搜索(brute force)算法啦。我把所有的情况都遍历一遍自然见分晓了。
template <class Comparable>
Comparable maxSubsequenceSum_quadratic(const vector<Comparable> &a,
int &seqStart, int &seqEnd)
{
int n = a.size();
Comparable maxSum = 0;
for (int i = 0; i < n; i++)
{
Comparable thisSum = 0;
for (int j = i; j < n; j++)
{
thisSum += a[j];
if (thisSum > maxSum)
{
maxSum = thisSum;
seqStart = i;
seqEnd = j;
}
}
}
return maxSum;
}
暴力搜索在解决小规模问题应该还是可以的,但是一旦问题的规模变大,问题就来了,我们看到这个程序有两重循环,也就是说它的复杂度是平方级别的,随着问题规模的增长,算法的复杂度是平方增长的,这自然不是我们愿意看到的。暴力搜索对解空间的全部元素进行了遍历,我们可不可以想一些办法,发觉这个问题的一些特征,缩小解空间的遍历范围呢?(在解线性规划的问题时,我们就曾经成功地利用了线性约束的凸集性质,把解的候选集缩小为约束区域的边界。)
所幸的是,我们找到了这个性质。
算法二 线性算法
我们先来看一下一个似乎显而易见的结论。
结论一:
如果数列A的某个子列 的和
,则
肯定不是数列A的最大递增子列。
这个结论告诉我们,i位置开始的子列,一旦遇到和为0的子列,后面可以不要搜索了,直接从i+1位置开始的子列搜索吧。且慢!只是这样吗?且看下一个结论:
结论二:
如果是数列A以i起始的子列中第一个和
的,则对任意
,
的和
要么小于最大连续子列和,要么与现存的最大连续子列和相等。
这个结论说穿了,就是跳过i到j这一段不会影响结果。
下面来解释一下这个结论:
Code
template <class Comparable>
Comparable maxSubsequenceSum_linear(const vector<Comparable> &a, int &seqStart, int &seqEnd)
{
int n = a.size();
Comparable maxSum = 0;
Comparable thisSum = 0;
for (int i = 0,j = 0; j < n;j++)
{
thisSum += a[j];
if (thisSum > maxSum)
{
maxSum = thisSum;
seqStart = i; seqEnd = j;
}
else if (thisSum < 0)
{
i = j + 1;
thisSum = 0;
}
}
return maxSum;
}
从程序可以看出,这个算法是级别的。相对于暴力算法,提高的是一个数量级的速度。怎么说?也就是暴力算法做一次的时间够它做n次了,这里n是问题的规模。
算法三 分治算法
这个问题到了算法二其实已经算是得到了比较圆满的解决。但是,我们还可以再想想,我们在解决很多问题的时候如:排序、顺序统计量的查找、FFT等平方级的算法时,都用了一个方法去解决,那就是“分治算法”。分治算法的神奇功效在于:把一个复杂的问题分解成一个个相似的简单的问题,解决这些简单的问题的适当组合来解决复杂的问题。这个算法,我觉得,在以后会越来越得到重视。因为目前CPU的主频在达到3.X GHz后就由于量子效应进展缓慢了,取而代之的是多核计算机的兴起。放眼望去,刚出来的计算机很多都是多核的,多核的目的在于发挥群体效应,期望达到人多势众的目的。这一目的的达到,需要实现算法的并行化,也就是尽量把解决问题的算法分解成几个子问题,让各个核分别同时去算,然后汇总结果。所谓并行即分治也!王能超在《算法演化论》中提到:“算法设计的基本理念是,通过简单的重复生成复杂,或者说,将复杂划归为简单的重复。”结合现在的趋势,我深以为然。
那么,我们现在尝试看看把问题分解分解吧。
分解有好几种,下面只分析我们用到的两种:
1. 规模分解。把问题的操作数据集分为两个部分,对两个子数据集分别操作,最后进行归并。这是FFT的做法。
2. 递推式分解。这方面的典型就是Fibonacci数列,其实它就是数学归纳法,假设我解决了规模为n-1的问题,那么我们需要再做点什么就能解决规模为n的问题呢?
下面,我们分别讨论这两种分解。
3.1规模分解

下面,同样给出源代码。(为了在一页内显示,采用了紧缩排版)
template <class Comparable>
Comparable maxSubsequenceSum_dac1(const vector<Comparable> &a, int left, int right,
int &seqStart, int &seqEnd)
{
int n = a.size();
Comparable maxSum = 0;
Comparable maxLeftBorderSum = 0, maxRightBorderSum = 0;
Comparable leftBorderSum = 0, rightBorderSum = 0;
BoundError e;
Comparable maxVal = 0;
try{
if (n <= right || left < 0 )
{ throw(BoundError(n,left,right)); }
if (n == 0) {return 0;}
if (left == right){
seqStart = seqEnd = left;
return a[left] > 0 ? a[left] : 0; }
int center = ((left + right) >> 1);
int lseqStart,lseqEnd,rseqStart,rseqEnd,lStart,rEnd;
Comparable maxLeftSum = maxSubsequenceSum_dac1(a,left,center,lseqStart, lseqEnd);
Comparable maxRightSum = maxSubsequenceSum_dac1(a,center+1,right,rseqStart, rseqEnd);
for (int i = center; i >= left; i--){
leftBorderSum += a[i];
if (leftBorderSum >= maxLeftBorderSum)
{ maxLeftBorderSum = leftBorderSum;
lStart = i;
}}
for (int j = center + 1; j <= right; j++){
rightBorderSum += a[j];
if (rightBorderSum >= maxRightBorderSum)
{ maxRightBorderSum = rightBorderSum;
rEnd = j;}}
if (maxLeftSum > maxLeftBorderSum + maxRightBorderSum){
maxVal = maxLeftSum;
seqStart = lseqStart,seqEnd = lseqEnd;}
else{ maxVal = maxLeftBorderSum + maxRightBorderSum;
seqStart = lStart,seqEnd = rEnd;}
if (maxVal < maxRightSum){
maxVal = maxRightSum;
seqStart = rseqStart,seqEnd = rseqEnd;}
}
catch(BoundError e){e.dispErr();}
return maxVal;}
代码提供了一个异常处理类,定义如下:
异常处理类:
class BoundError
{
public:
BoundError(int a, int b, int c)
{
sprintf(err,"BoundError,vector size:%d, left:%d, right: %d",a,b,c);
}
BoundError(){}
void dispErr() const {cout<< err<<endl;}
private:
char err[200];
};
这个代码代码量看上去比上面大许多,时间复杂度也比不上线性算法,但是并不是每个问题都有那么幸运能偶找到一个线性算法的,这时候
的算法带来的提升已经很可观了,这就是为什么Turkey的FFT被评为20世纪是十大算法的原因。另外在工程上,任何提升都是有代价的,这里代码量的增加就是平方时间复杂度的问题提升到对数时间复杂度所需要的代价。“没有免费的午餐”是永恒的真理。
3.2递推式分解
递推式分解其实就是数学归纳法的生动体现,我们学过辩证法,知道归纳和推理是真理的两大来源,而归纳由于其所需要的感性知识比推理远来得多,显得尤为难得从而产生的成果也更为可贵。
现在的问题是:如果现在我知道了规模为n-1的数列的最大递增子列的结果,现在在这个子列后面又添了一个元素,现在如何根据现有的结果更新新的数列的结果。
其实,可能有人已经看出来了,递推分解就是前面规模分解的一种极限形式,把一个问题分解为n-1和1两个部分。同样地,也有三种情形:
Case 1: 最大递增子列全部在n-1的数列中;
Case 2: 就是最后一个数;
Case 3: 是n-1的数列的后缀和最后一个数的组合。
现在我们知道了,我们只要知道n-1的数列的最大递增子列以及最大后缀子列就行了。
下面我们就可以着手实现了。我们看一下下面的代码就知道,数学归纳是递推,而规模分解是递归,虽然本质思想都是一样的divide and conquer,但是正如我之前的Fibonacci数列的文章中分析的一样,其实现代价和算法效率是不一样的,显然这个算法的效率是。
template <class Comparable>
Comparable maxSubsequenceSum_dac2(const vector<Comparable> &a, int &seqStart, int &seqEnd)
{
int n = a.size();
Comparable MaxSum = 0;
Comparable MaxSuffix = 0;
for (int i = 0; i < n; i++)
{
if (MaxSuffix + a[i] > MaxSum)
{
MaxSuffix += a[i];
MaxSum = MaxSuffix;
seqEnd = i;
}
else
if (MaxSuffix + a[i] > 0)
{
MaxSuffix += a[i];
}
else
{
MaxSuffix = 0;
}
}
int max_v = 0;
int end = seqEnd;
while(max_v < MaxSum)
{
max_v += a[end--];
}
seqStart = end + 1;
return MaxSum;
}
性能测试:
下面对上述四种算法进行了性能测试。
测试环境:
操作系统:windows xp
CPU : Intel(R) T2080 1.73GHz
内存 :1.73GHz,504MB
结果:
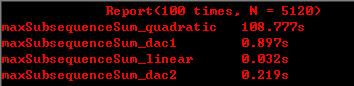
后记:
这篇文章的空文档在我的电脑里躺了一年,始终只有一个题目,电脑里有很多这样的文档。今天花一天整理了一个问题,也终于开始了重新捡起地上丢下的棒子的旅程。这些问题都是一些小问题,但是却都是“麻雀虽小,五脏俱全”。下一站—LZW算法。
参考文献:
1. Mark Allen Weiss 数据结构与问题求解(C++版) 清华大学出版社
2. Udi Manber 算法引论-一种创造性方法 电子工业出版社
3. Walter Savitch 完美C++教程 清华大学出版社
附注:
由于本文的代码使用了函数模板,因此如果是C++的初学者要使用本文的函数请注意:
许多编译器不支持对模板的单独编译,因此你必须在代码中使用模板的地方包含模板的定义。通常情况下,至少要保证模板函数的声明要早于函数的模板的使用。
…
能保证在绝大多数的C++的编译器上对模板程序编译成功地布局如下:将模板的定义与使用模板的函数放在一个文件中,并且保证模板的定义出现在所有使用模板的代码之前。如果你想将函数模板的定义放在一个与你的应用程序不同的单独的文件中,可以使用#includes命令在需要使用该模板的文件中将函数模板的定义包含进来。
———— 摘自《完美C++教程》
以上所有程序均编译运行正常。如出现模板函数的相关问题,请请教高手,因为我也是第一次使用模板函数,所以也不懂,呵呵。




