选择排序/插入排序/冒泡排序
选择排序
首先在这整个数组范围里找到最小的元素1，然后和第一名的位置交换，之后我们在剩下的部分再找最小的元素2，把2和第二名的位置来交换，以此类推。
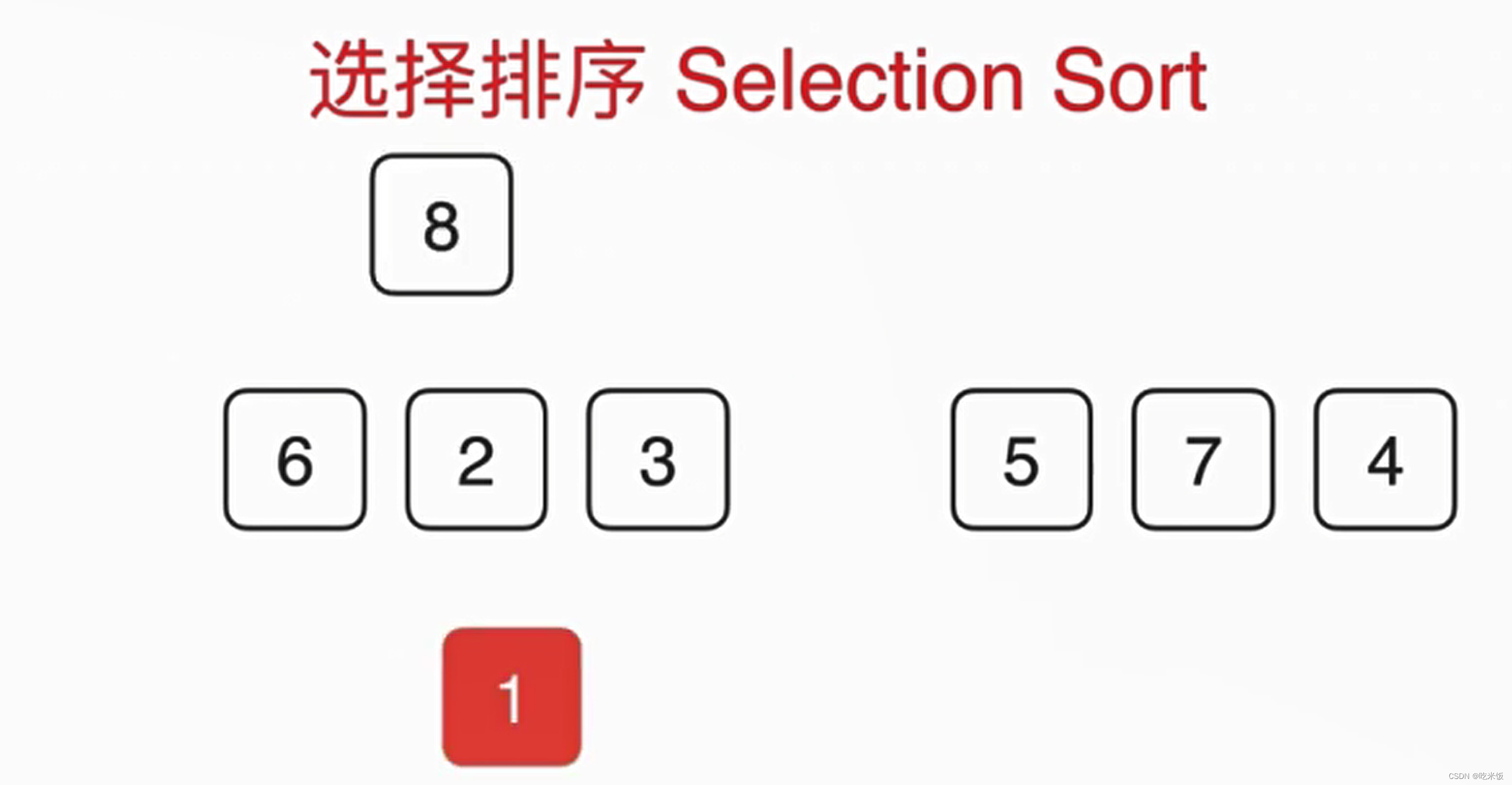
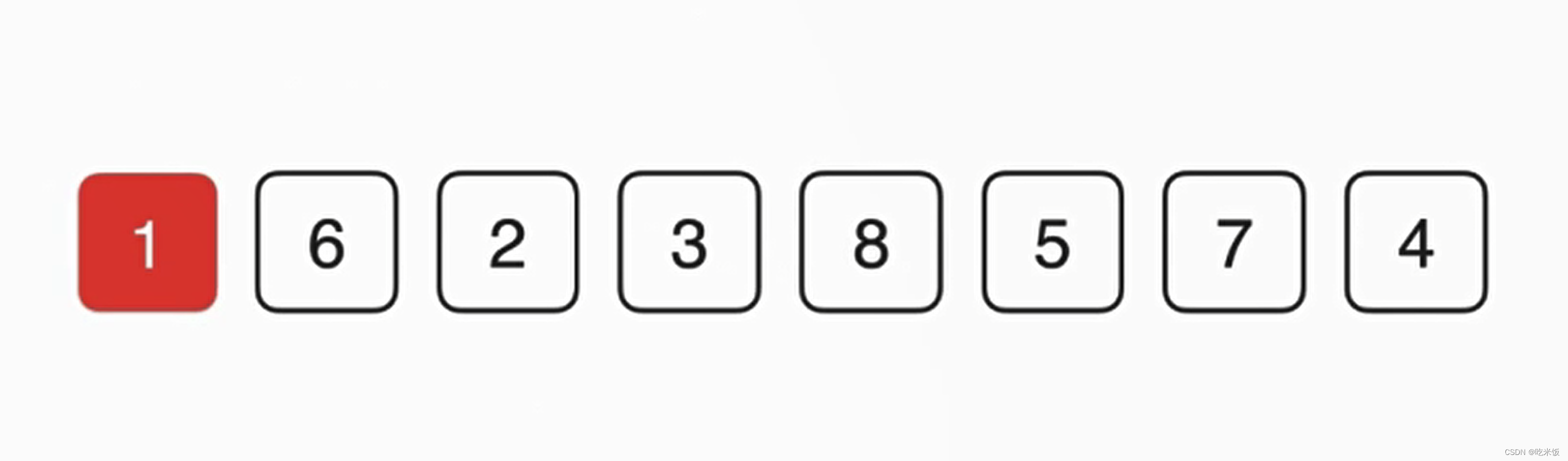
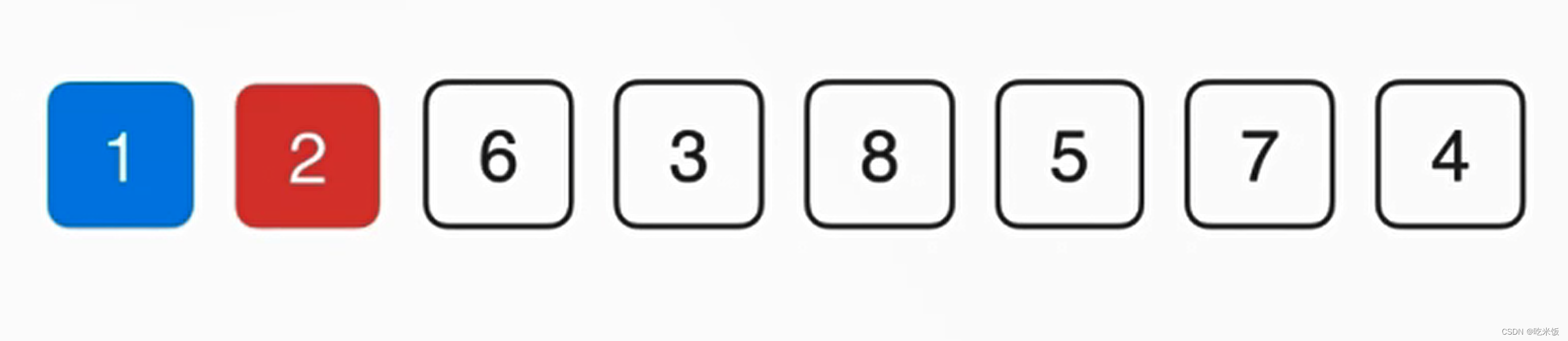
selectionSort
template<typename T>
void selectionSort(T arr[], int n) {
for (int i = 0; i < n; ++i) {
int minIndex = i;
for (int j = i + 1; j < n; ++j) {
if (arr[minIndex] > arr[j]) {
minIndex = j;
}
}
std::swap(arr[i], arr[minIndex]);
}
}
优化
// 在每一轮中, 可以同时找到当前未处理元素的最大值和最小值
template<typename T>
void selectionSort(T arr[], const int n) {
int left = 0, right = n - 1;
while (left < right) {
int minIndex = left;
int maxIndex = right;
// 在每一轮查找时, 要保证arr[minIndex] <= arr[maxIndex]
if (arr[minIndex] > arr[maxIndex]) {
std::swap(arr[minIndex], arr[maxIndex]);
}
for (int i = left + 1; i < right; i++) {
if (arr[i] < arr[minIndex]) {
minIndex = i;
} else if (arr[i] > arr[maxIndex]) {
maxIndex = i;
}
}
std::swap(arr[left], arr[minIndex]);
std::swap(arr[right], arr[maxIndex]);
left++;
right--;
}
}
插入排序
对于第一个元素我们不动，因为当我们只考虑8这个元素是它已经是有序的了，我们要看的是6这个元素，对于这个元素我们要的是把它放到前面合适的位置，跟它前面的8相比6比8小索引它们要调换一下位置，此时前两个元素就有序了，以此类推。
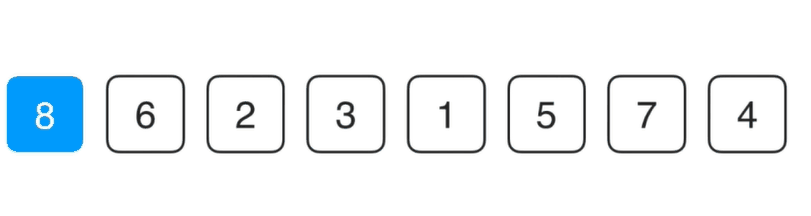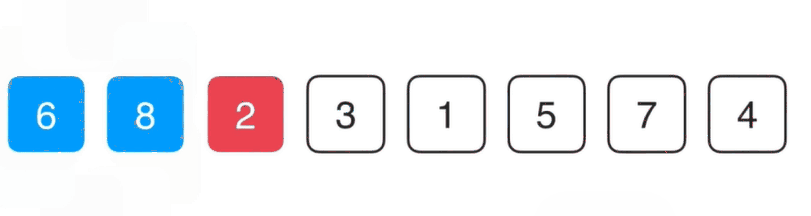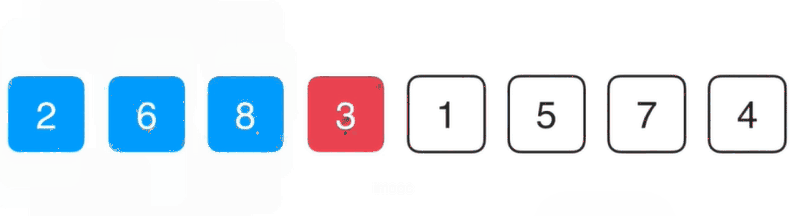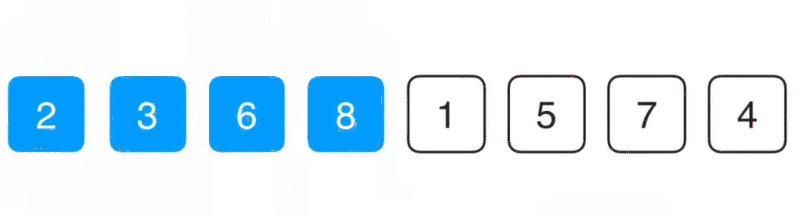
insertionSort
//插入排序
template<typename T>
void insertionSort(T arr[], const int n) {
for (int i = 1; i < n; i++) {
// 寻找元素arr[i]合适的插入位置
// 写法1
// for( int j = i ; j > 0 ; j-- )
// if( arr[j] < arr[j-1] )
// swap( arr[j] , arr[j-1] );
// else
// break;
// 写法2
for (int j = i; j > 0 && arr[j] < arr[j - 1]; --j) {
std::swap(arr[j], arr[j - 1]);
}
}
}
优化交换为赋值
首先对于第零个元素8保持不变，然后考察6，先把6赋值一份，然后看看6是不是适合放在当前的位置，就和前面的元素做比较，如果和前一元素要小就说明不应该放在当前的这个位置，而8因该放在当前的这个位置，所以把8向后挪一位，之后再考察6是不是因该放在前一位置，以此类推。
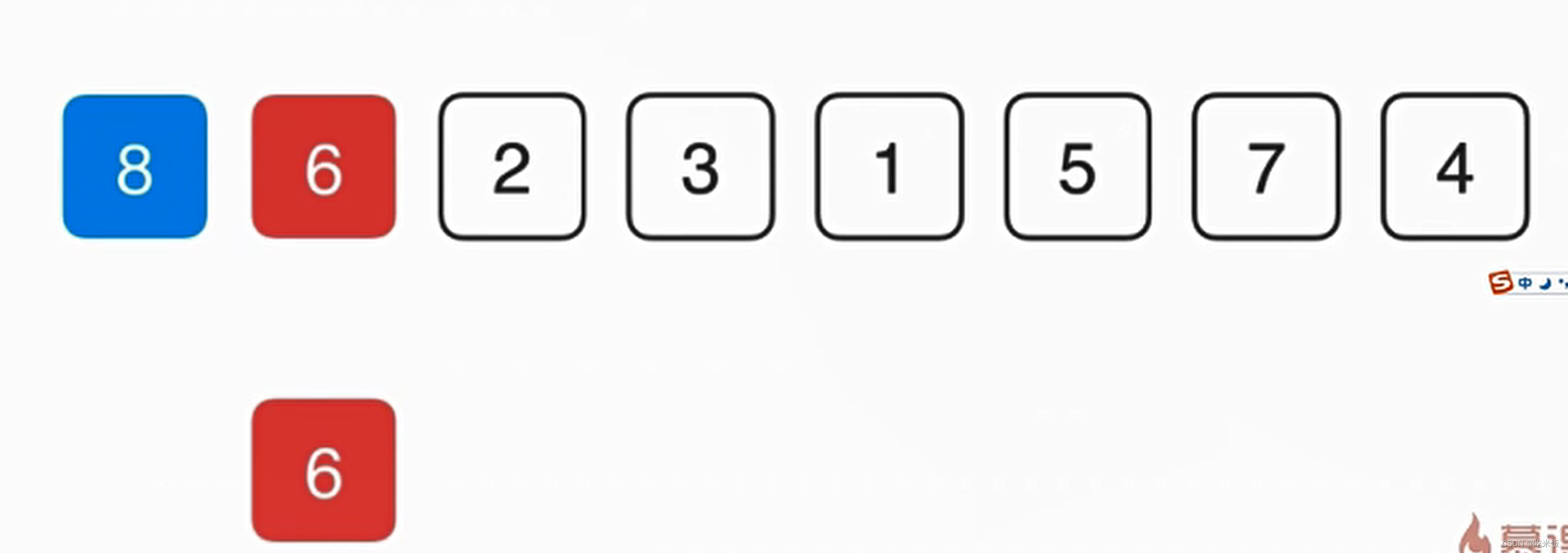
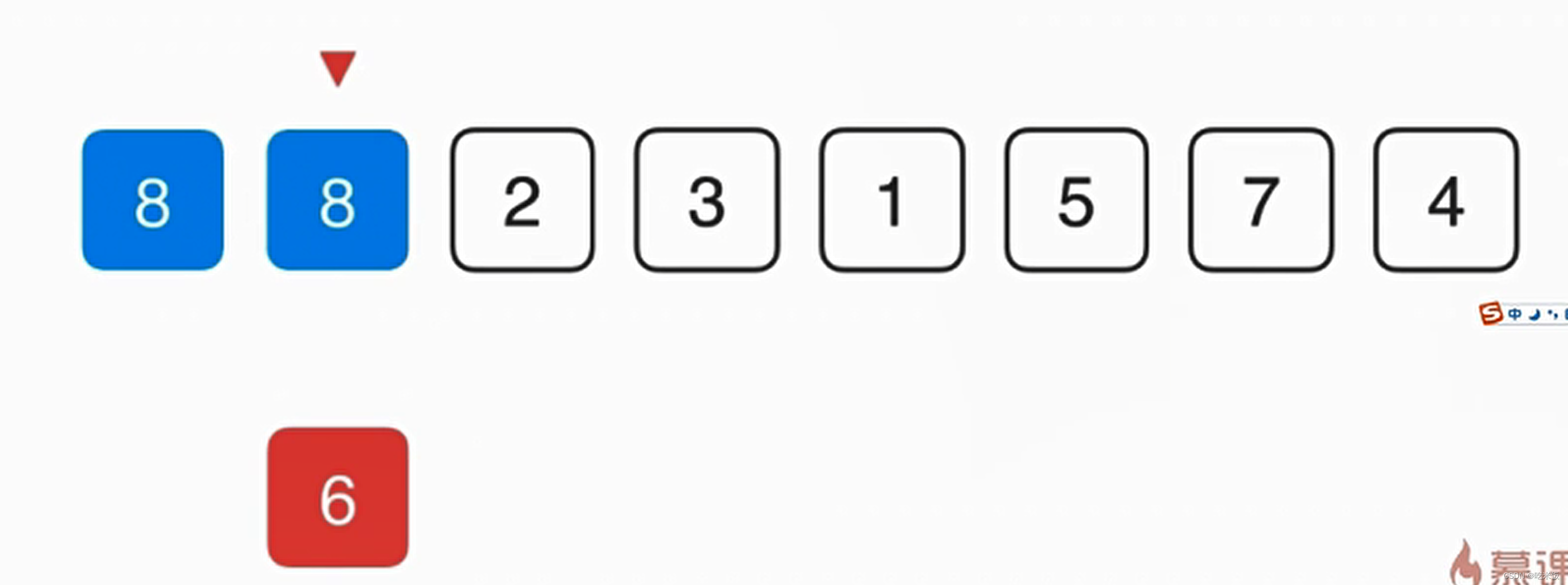
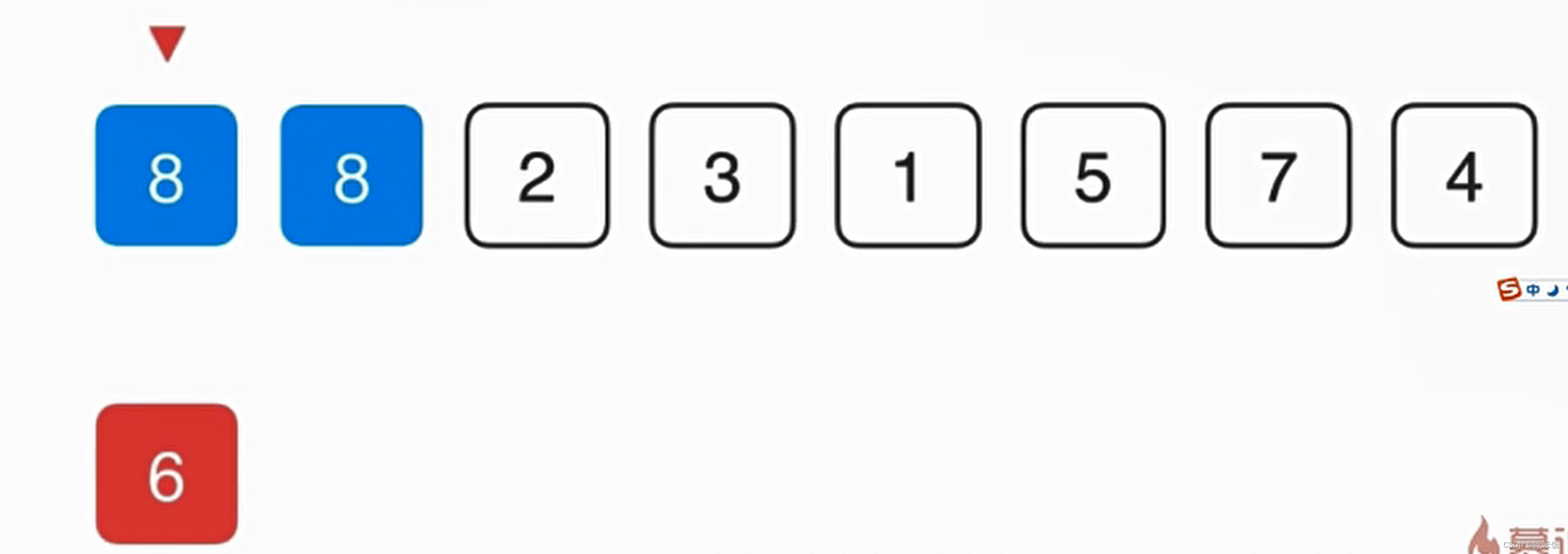
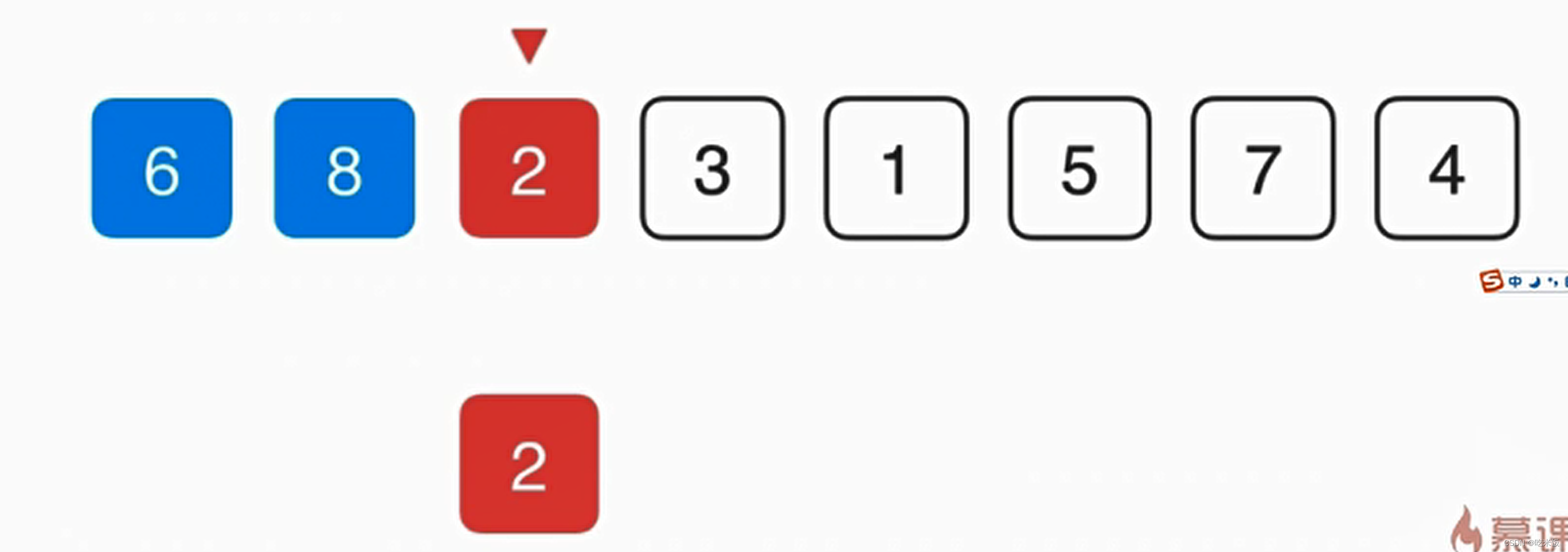
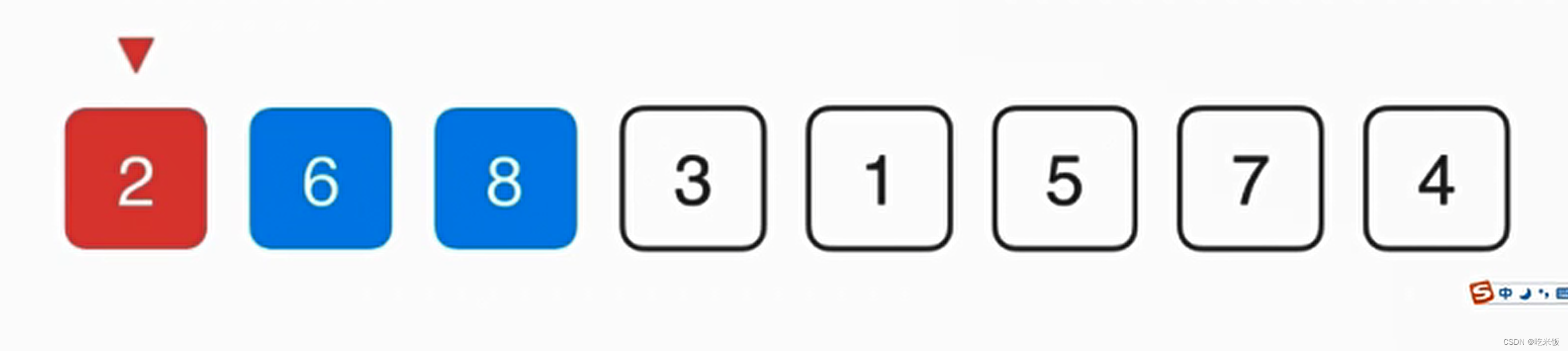
- 如此对于近乎有序的序列插入排序非常高效，以至于相比较O(nlogn)级别的算法还要快。在一个完全有序的数组中，他会进化成一个O(n)级别的算法，所以插入排序常用于算法的优化中。
//插入排序
template<typename T>
void insertionSort(T arr[], const int n) {
for (int i = 1; i < n; i++) {
// 寻找元素arr[i]合适的插入位置
T e = arr[i];
int j; // j保存元素e应该插入的位置
for (j = i; j > 0 && arr[j - 1] > e; j--) {
arr[j] = arr[j - 1];
}
arr[j] = e;
}
}
冒泡排序
bubbleSort
//冒泡排序
template<typename T>
void bubbleSort(T arr[], const int n) {
for (int i = 0; i < n - 1; ++i) {
for (int j = 0; j < n - i - 1; ++j) {
if (arr[j] > arr[j + 1]) {
std::swap(arr[j], arr[j + 1]);
}
}
}
}
优化
//优化
template<typename T>
void bubbleSort(T arr[], const int n) {
bool isSwapped;
int lastSwap = 0;
int k = n - 1;
for (int i = 0; i < n; ++i) {
//记录当某一一轮是否发生交换行为，若为发生则判定已经排序成功，跳出循环即可。
isSwapped = false;
for (int j = 0; j < k; ++j) {
if (arr[j] > arr[j + 1]) {
arr[j] = arr[j] ^ arr[j + 1];
arr[j + 1] = arr[j + 1] ^ arr[j];
arr[j] = arr[j] ^ arr[j + 1];
isSwapped = true;
/*记录一轮交换后的最终索引，通过观察发现这个索引后的数字都是有序的，
* 那么以后就不用比较这个索引后面的数字，即内层循环的边界是前面所说的最终索引。
* 当这个最终索引为0的时候（即前面没有数字的时候）排序就结束了。
* */
lastSwap = j;
}
}
if (!isSwapped) break;
k = lastSwap;
}
}
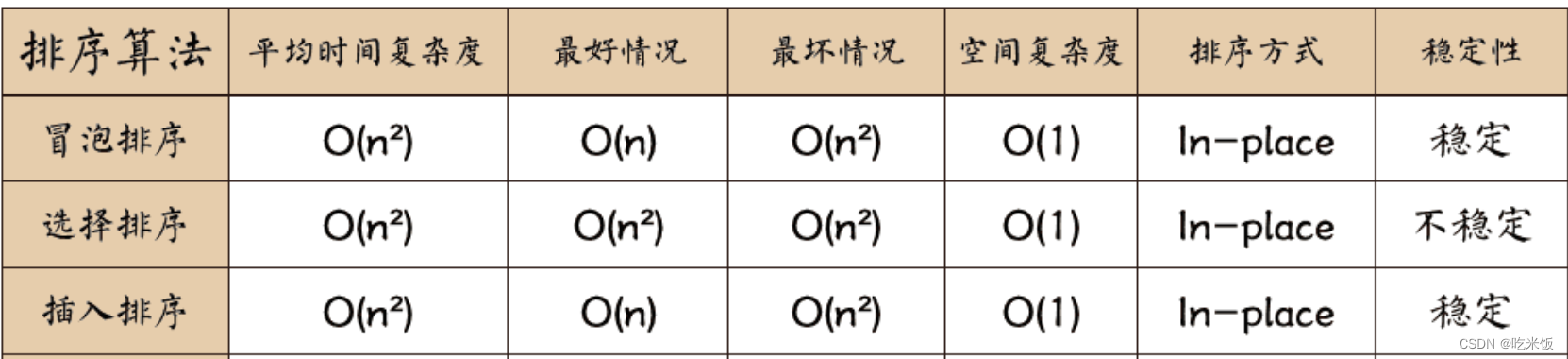
概括
