最大堆(MaxHeap)
性质
- 二叉堆是一颗完全二叉树,而完全二叉树是把元素排列成树的形状。
- 堆中某个节点的值总不大于其父节点的值最大堆(相应的可以定于最小堆)
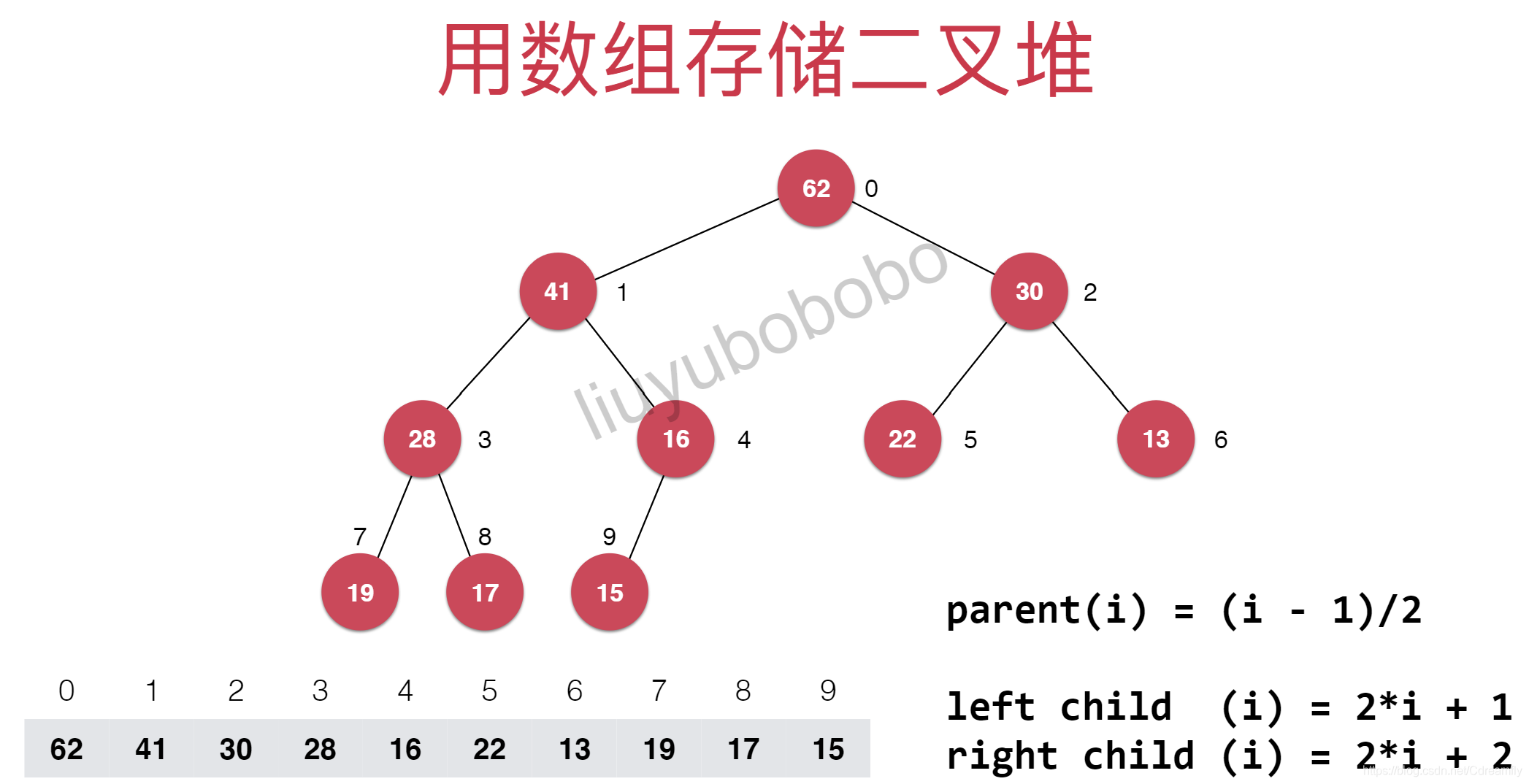
// 返回完全二叉树的数组表示中,一个索引所表示的元素的父亲节点的索引
constexpr int parent(const int index) const {
if (index == 0) {
throw new NoParent();
}
return (index - 1) / 2;
}
// 返回完全二叉树的数组表示中,一个索引所表示的元素的左孩子节点的索引
constexpr int leftChild(const int index) const {
return (index * 2) + 1;
}
// 返回完全二叉树的数组表示中,一个索引所表示的元素的右孩子节点的索引
constexpr int rightChild(const int index) const {
return (index * 2) + 2;
}
可以先阅读底层动态数组Array
添加
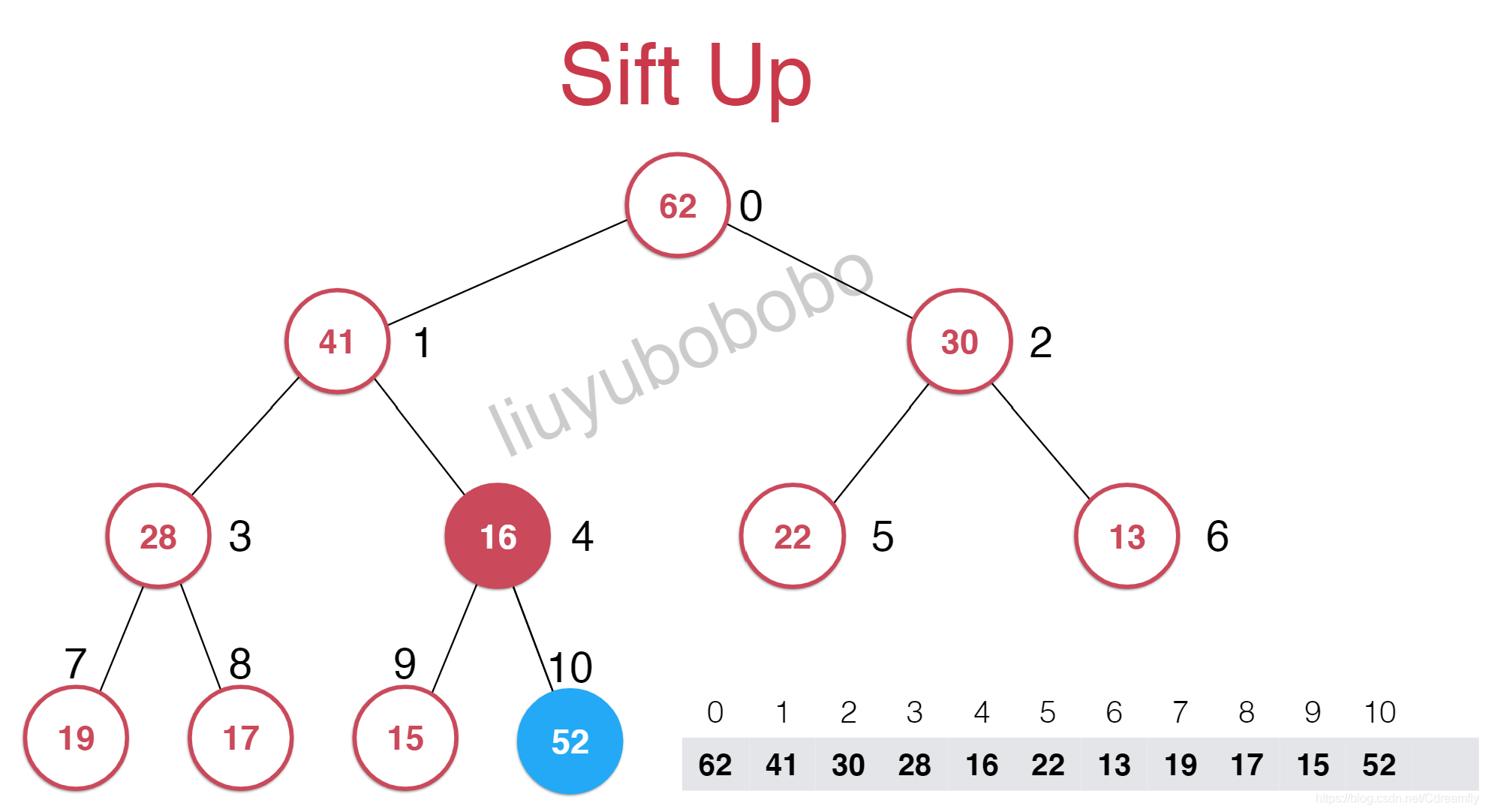
首先我们堆中的数据使用数组排列的,所以添加一个元素就是在层序遍历的最右端,也就是最下面一层的最后添加一个元素。但是以数组来看就是在索引为10的地方添加一个元素。
void add(const T &e) {
data->addLast(e); //在数组的末尾添加元素
shiftUp(data->getSize() - 1); //上浮添加元素的索引
}
- 时间复杂度O(logn)
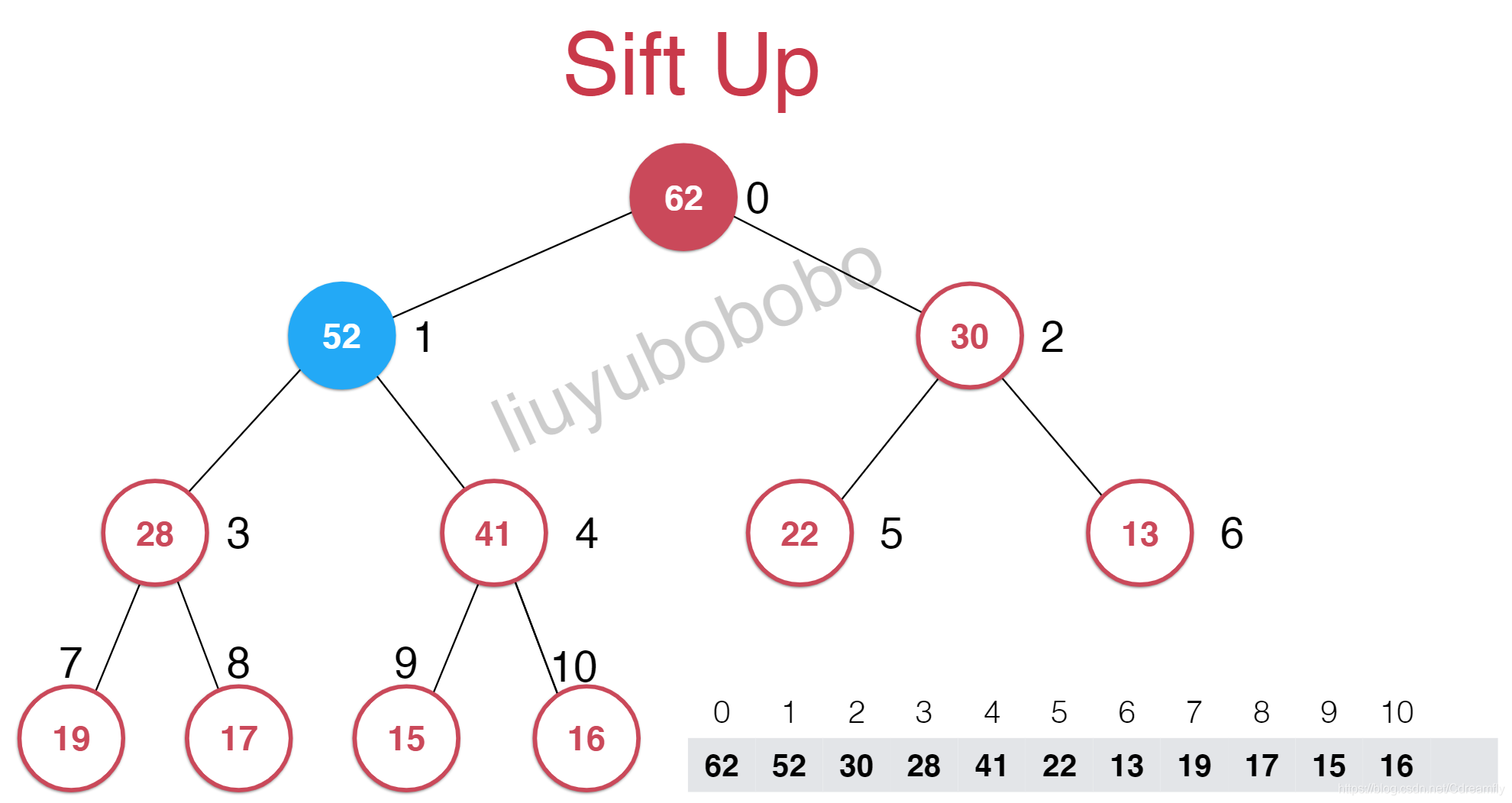
但是添加的元素不符最大堆的性质,索引我需要一些调整,而这个调整就是一个上浮的过程。
void shiftUp(int index) {
//如果传入索引小于等于0并且父元素大于等于子元素则停止循环
while (index > 0 && data->get(index) > data->get(parent(index))) {
data->swap(index, parent(index)); //位置交换
index = parent(index); //把父节点的索引给子节的
}
}
取出最大元素
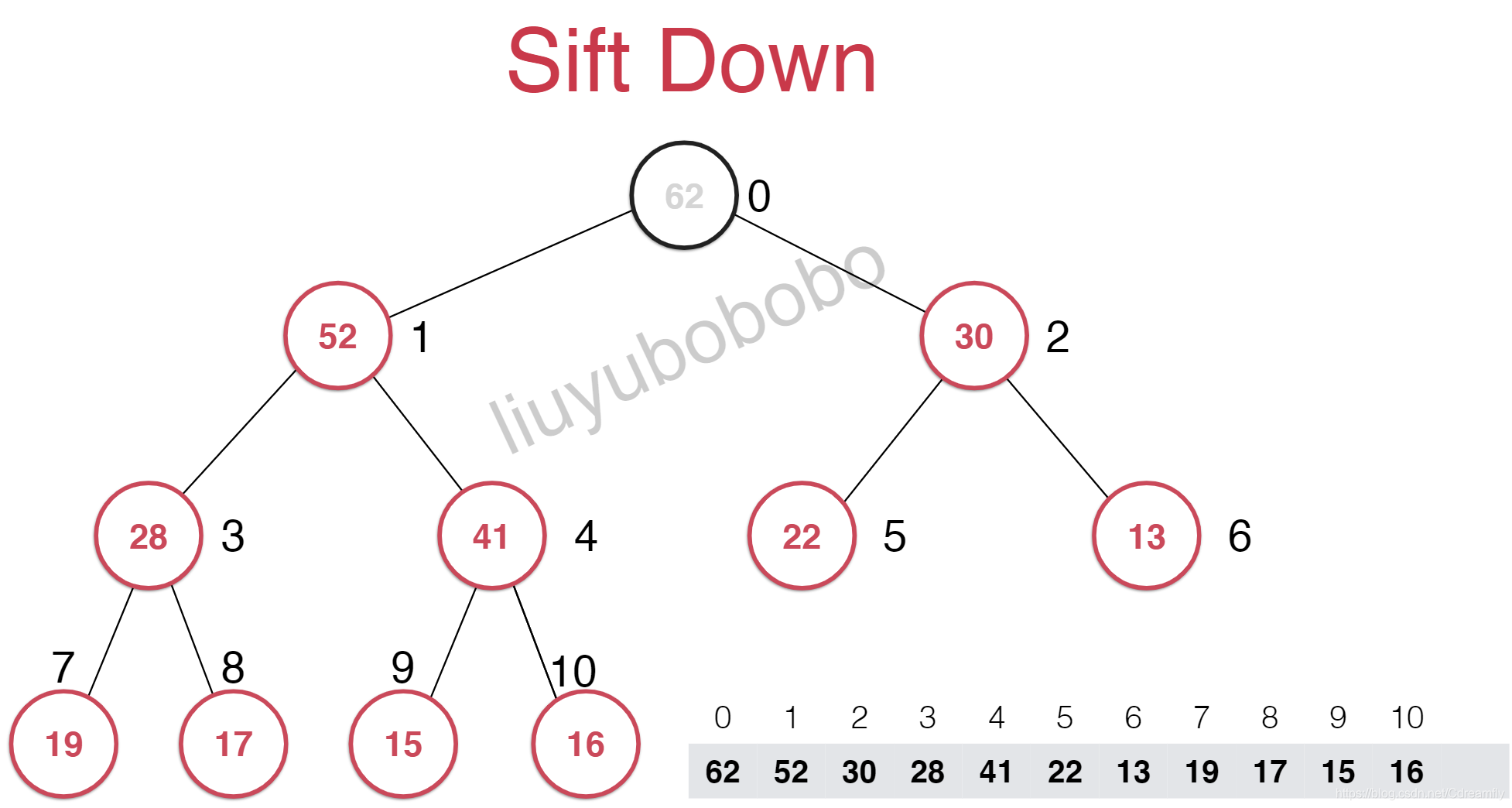
最大堆的最大元素就是其根节点元素,取出的操作只能取出这个元素,对于数组来说,根结点就是索引为0的元素。
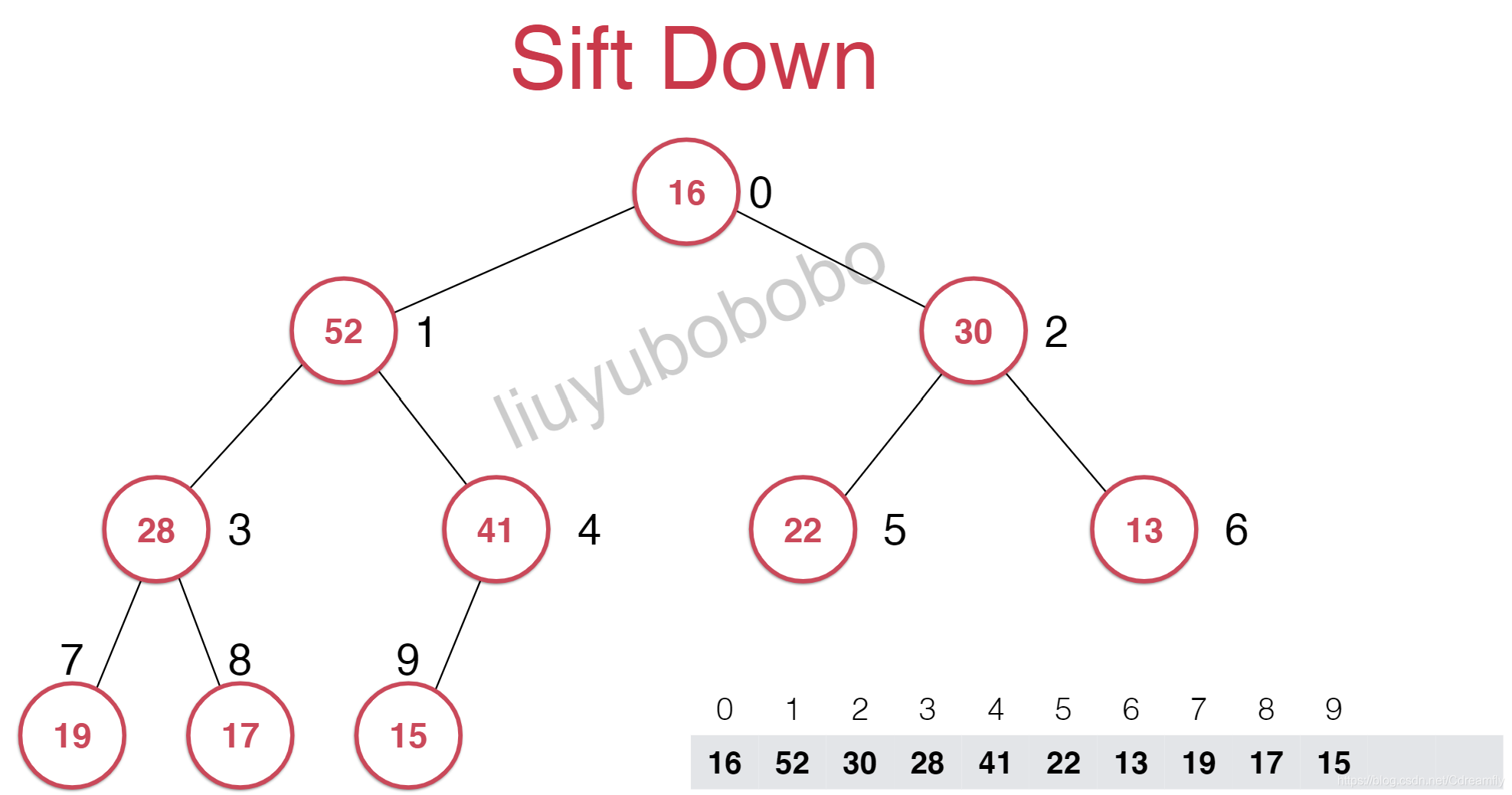
我们把堆中最后一个元素顶到堆顶去,然后再把最后一个元素删除。然而这样就又不符合最大堆的性质。
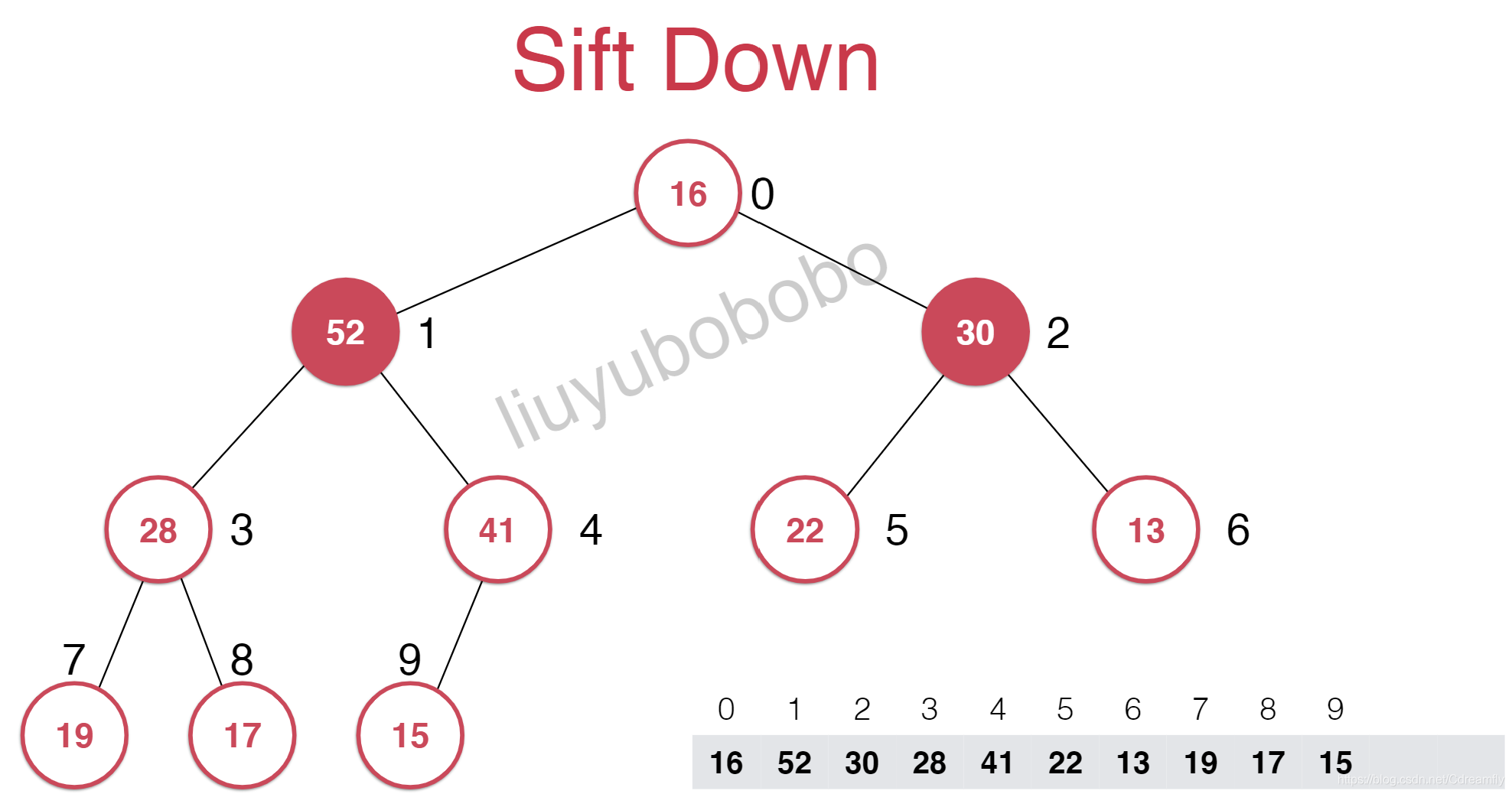
这样的话,其不大于它的子节点,此时又要进行调整,这个调整的过程叫做下沉。在这个过程中每次需要下沉的时候都要和它的两个孩子进行比较,选择其中较大的进行交换位置。
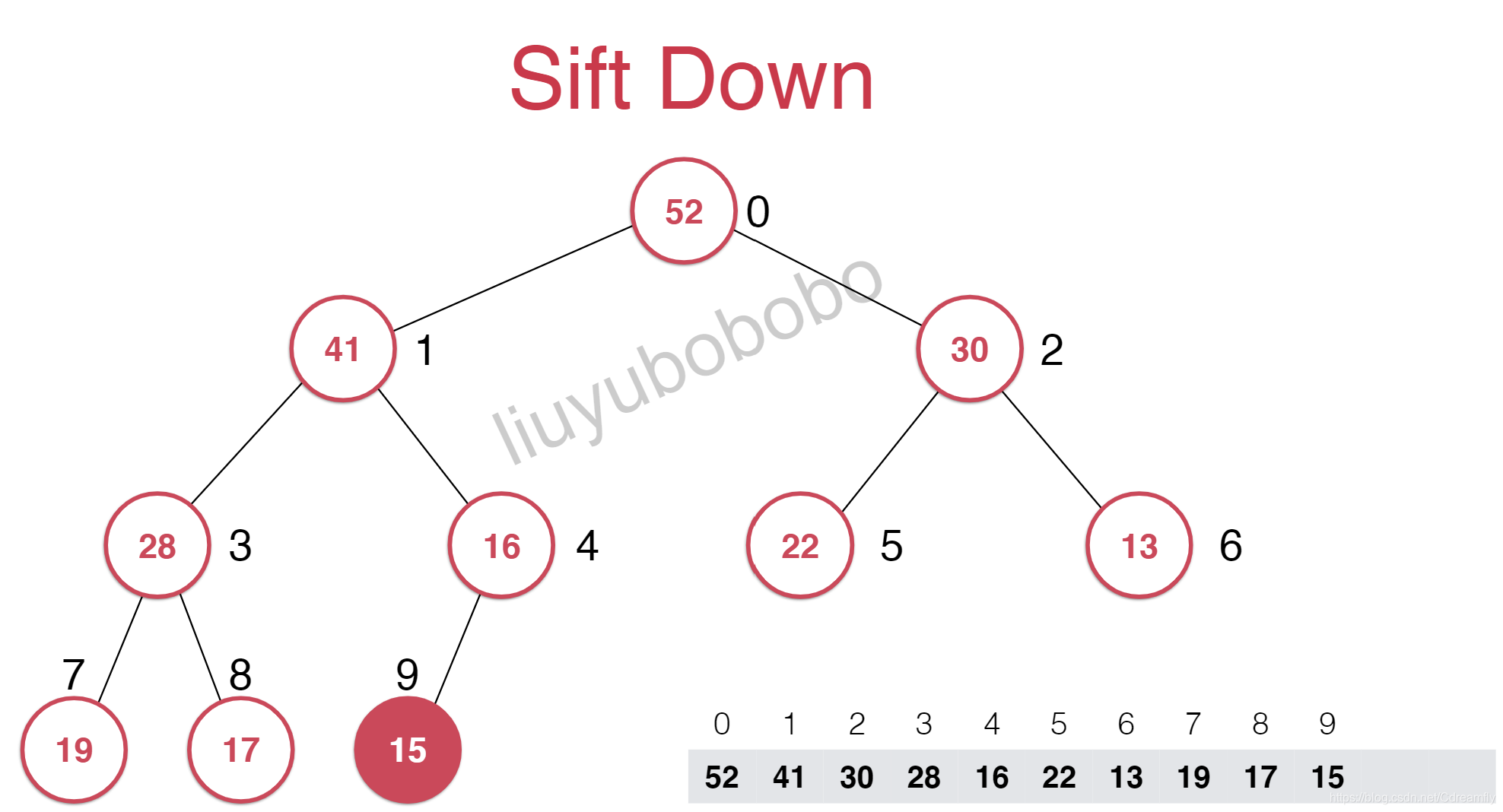
- 时间复杂度O(logn)
//返回最大的元素
T findMax() const {
if (data->isEmpty()) {
throw Empty();
}
return data->get(0);
}
//取出最大的元素
T extractMax() {
T ret = findMax();
data->swap(0, data->getSize() - 1);
data->removeLast();
shiftDown(0);
return ret;
}
//下沉
void shiftDown(int k) {
while (leftChild(k) < data->getSize()) {
int j = leftChild(k);
//j保存的是左右孩子中较大的元素索引
if (j + 1 < data->getSize() && data->get(j + 1) > data->get(j)) {
j = rightChild(k);
}
//如果子节点小于等于父节点了,就结束
if (data->get(k) > data->get(j)) {
break;
}
data->swap(k, j);
k = j;
}
}
取出堆中最大的元素,并替换成元素e
- 时间复杂度O(logn)
T replace(T e) {
T ret = findMax();
data->set(0, e);
shiftDown(0);
return ret;
}
Heapify
将n个元素逐个插入到一个空堆中,算法复杂度是O(nlogn),Heapify的过程,算法复杂度是O(n)。
MaxHeap(T arr[], const int n) {
data = new Array<T>(arr, n);
for (int i = parent(n - 1); i >= 0; --i) {
shiftDown(i);
}
}
对比使用与不适用Heapify代码
#include <iostream>
#include "MaxHeap.h"
#include <cassert>
template<typename T>
double testHeap(T testData[], int n, bool isHeapify) {
clock_t startTime = clock();
MaxHeap<T> *maxHeap;
if (isHeapify) {
maxHeap = new MaxHeap<T>(testData, n);
} else {
maxHeap = new MaxHeap<T>();
for (int i = 0; i < n; ++i) {
maxHeap->add(testData[i]);
}
}
T *arr = new T[n];
for (int j = 0; j < n; ++j) {
arr[j] = maxHeap->extractMax();
}
for (int k = 1; k < n; ++k) {
assert(arr[k - 1] >= arr[k]);
}
std::cout << "Test MaxHeap completed." << std::endl;
clock_t endTime = clock();
return double(endTime - startTime) / CLOCKS_PER_SEC;
}
int main() {
int n = 5000000;
int *testData = new int[n];
for (int i = 0; i < n; ++i) {
testData[i] = rand() % INT32_MAX;
}
double time1 = testHeap(testData, n, false);
std::cout << "Without heapify :" << time1 << " s " << std::endl;
double time2 = testHeap(testData, n, true);
std::cout << "With heapify :" << time2 << " s " << std::endl;
return 0;
}
代码清单
//
// Created by cheng on 2021/7/10.
//
#ifndef MAXHEAP_MAXHEAP_H
#define MAXHEAP_MAXHEAP_H
#include "Array.h"
template<typename T>
class MaxHeap {
public:
class NoParent {
};
class Empty {
};
MaxHeap() {
data = new Array<T>();
}
~MaxHeap() {
delete data;
data = nullptr;
}
MaxHeap(const int capacity) {
data = new Array<T>(capacity);
}
MaxHeap(T arr[], const int n) {
data = new Array<T>(arr, n);
for (int i = parent(n - 1); i >= 0; --i) {
shiftDown(i);
}
}
constexpr int getSize() const {
return data->getSize();
}
constexpr bool isEmpty() const {
return data->isEmpty();
}
// 返回完全二叉树的数组表示中,一个索引所表示的元素的父亲节点的索引
constexpr int parent(const int index) const {
if (index == 0) {
throw new NoParent();
}
return (index - 1) / 2;
}
void add(const T &e) {
data->addLast(e);
shiftUp(data->getSize() - 1);
}
//返回最大元素
T findMax() const {
if (data->isEmpty()) {
throw Empty();
}
return data->get(0);
}
//取出最大的元素
T extractMax() {
T ret = findMax();
data->swap(0, data->getSize() - 1);
data->removeLast();
shiftDown(0);
return ret;
}
//取出堆中最大的元素,并替换成元素e
T replace(T e) {
T ret = findMax();
data->set(0, e);
shiftDown(0);
return ret;
}
void print() {
data->print();
}
private:
void shiftDown(int k) {
while (leftChild(k) < data->getSize()) {
int j = leftChild(k);
if (j + 1 < data->getSize() && data->get(j + 1) > data->get(j)) {
j = rightChild(k);
}
if (data->get(k) > data->get(j)) {
break;
}
data->swap(k, j);
k = j;
}
}
void shiftUp(int index) {
while (index > 0 && data->get(index) > data->get(parent(index))) {
data->swap(index, parent(index));
index = parent(index);
}
}
// 返回完全二叉树的数组表示中,一个索引所表示的元素的左孩子节点的索引
constexpr int leftChild(const int index) const {
return (index * 2) + 1;
}
// 返回完全二叉树的数组表示中,一个索引所表示的元素的右孩子节点的索引
constexpr int rightChild(const int index) const {
return (index * 2) + 2;
}
private:
Array<T> *data;
};
#endif //MAXHEAP_MAXHEAP_H


