UE5 材质 Water Shader
目标
- 水有许多特性,本篇将着重实现如下特性
- 表面涟漪
- 水深效果
- 水的反射和折射
- 海浪
- 波光的焦散
表面涟漪
初步实现
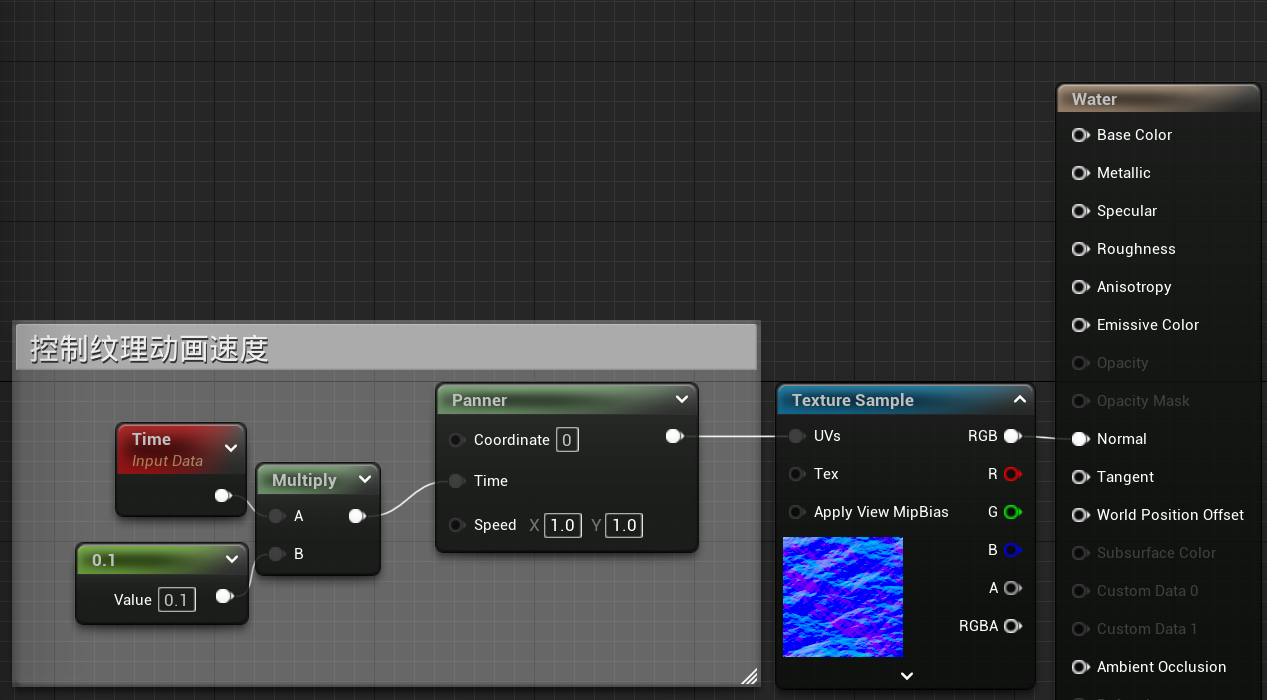

模拟水的运动
- 现实中水的流动是较为混乱的,但上图的水流动过于统一。我们使用世界坐标的位置进行投影,且让水只在XY平面进行运动
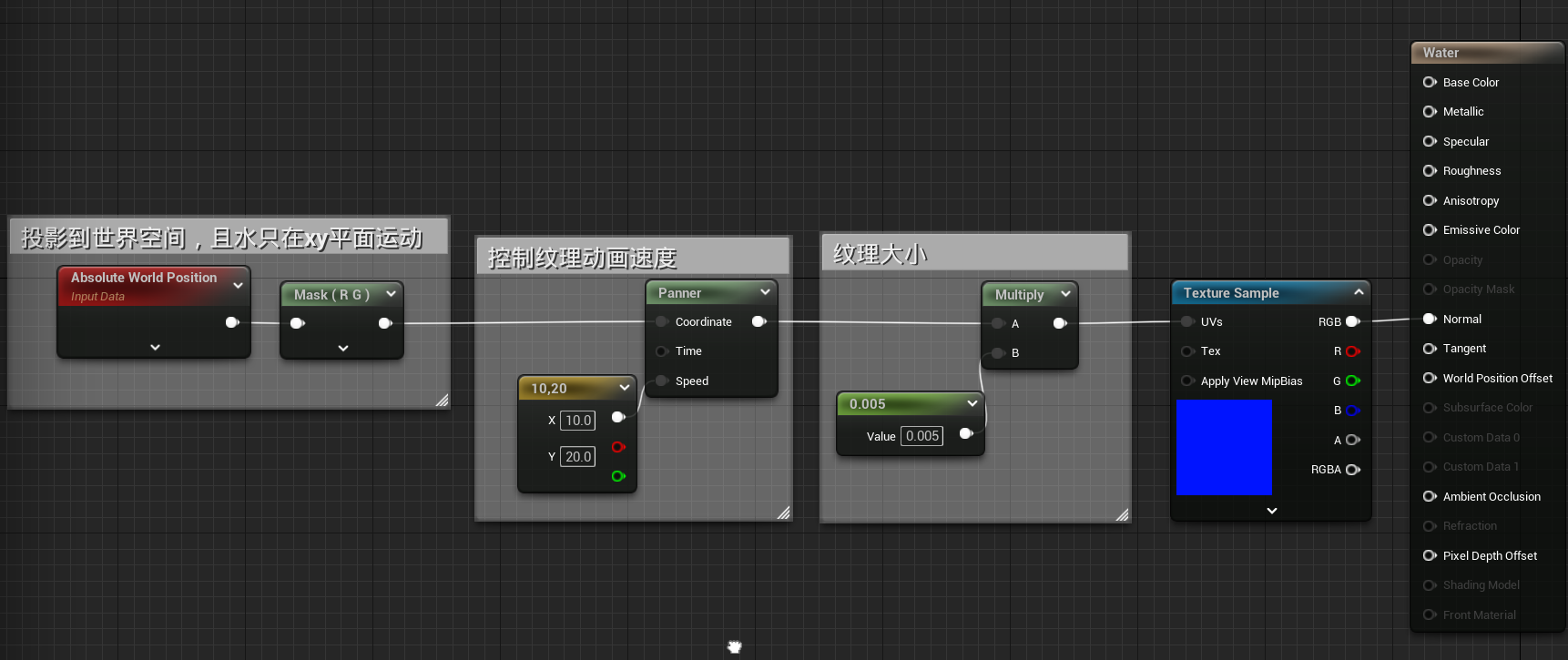
- 如何让水的流动混乱呢?很容易想到,我们需要让纹理图在不同方向上进行变换
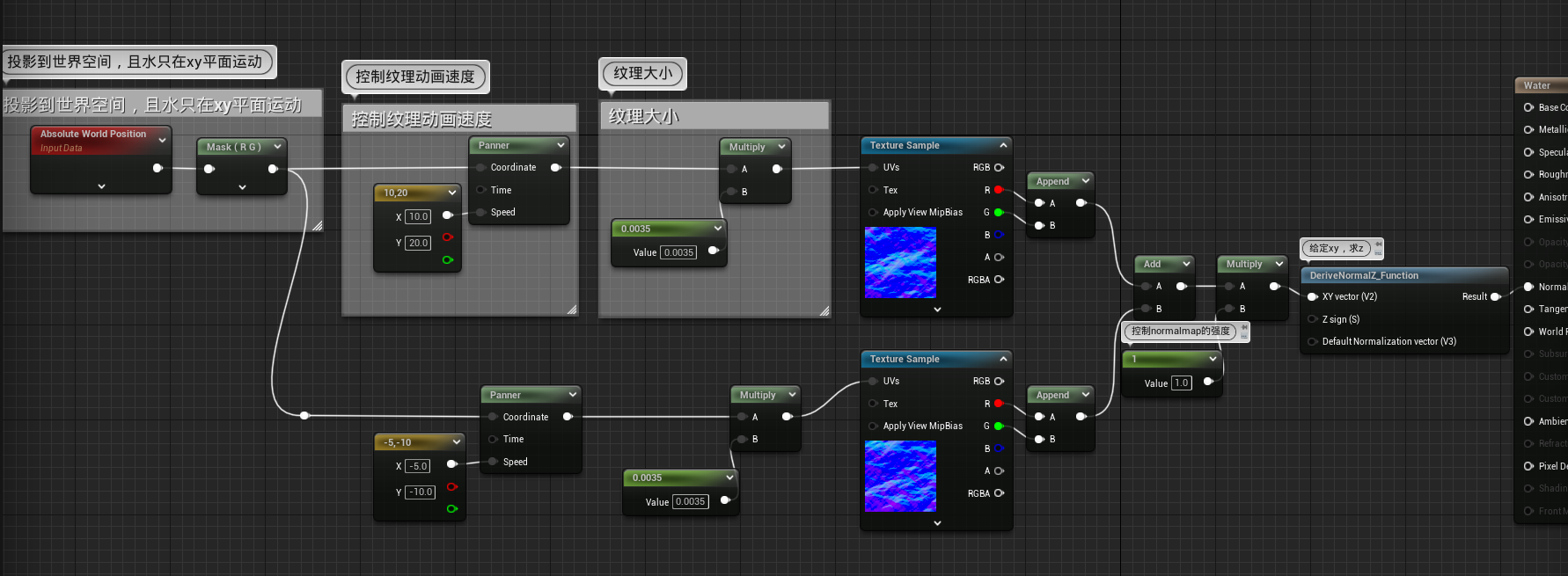

水深
影响水透明度的因素
- 看向水面的角度
- 水深。水越深,会变得越来越不透明
设置blend mode
- 因为这里涉及到半透明渲染,我们需要选择"Blend Mode"为"Translucent"
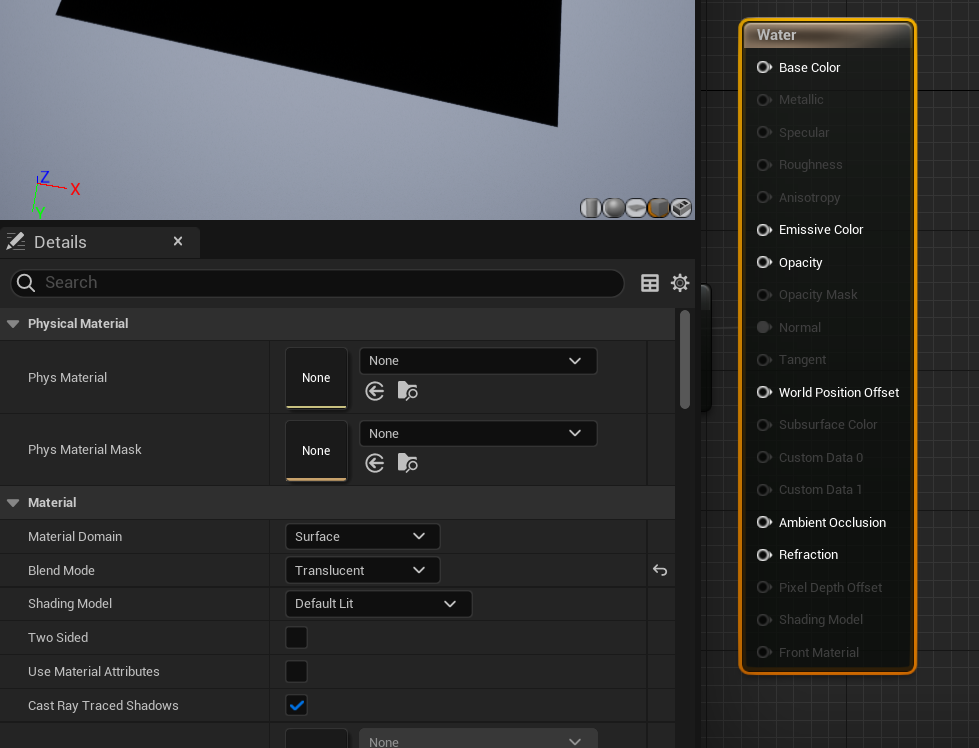
测量水深
"SceneDepth" & "PixelDepth"
步骤
- SceneDepth:以相机为视角,返回场景中离它最近的一个物体的距离且忽略透明物体
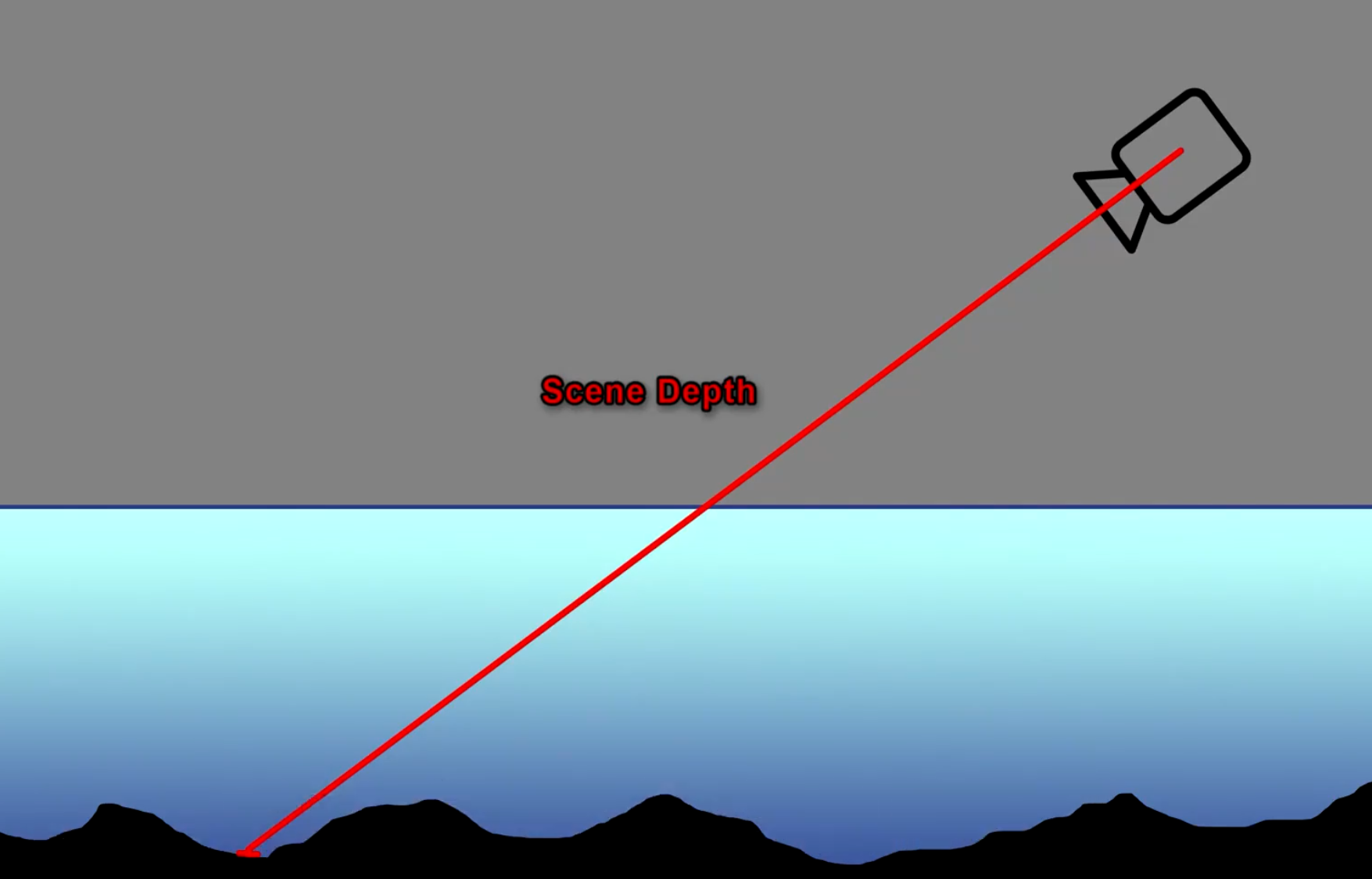
- PixelDepth:以相机为视角,返回它到半透明物体的距离
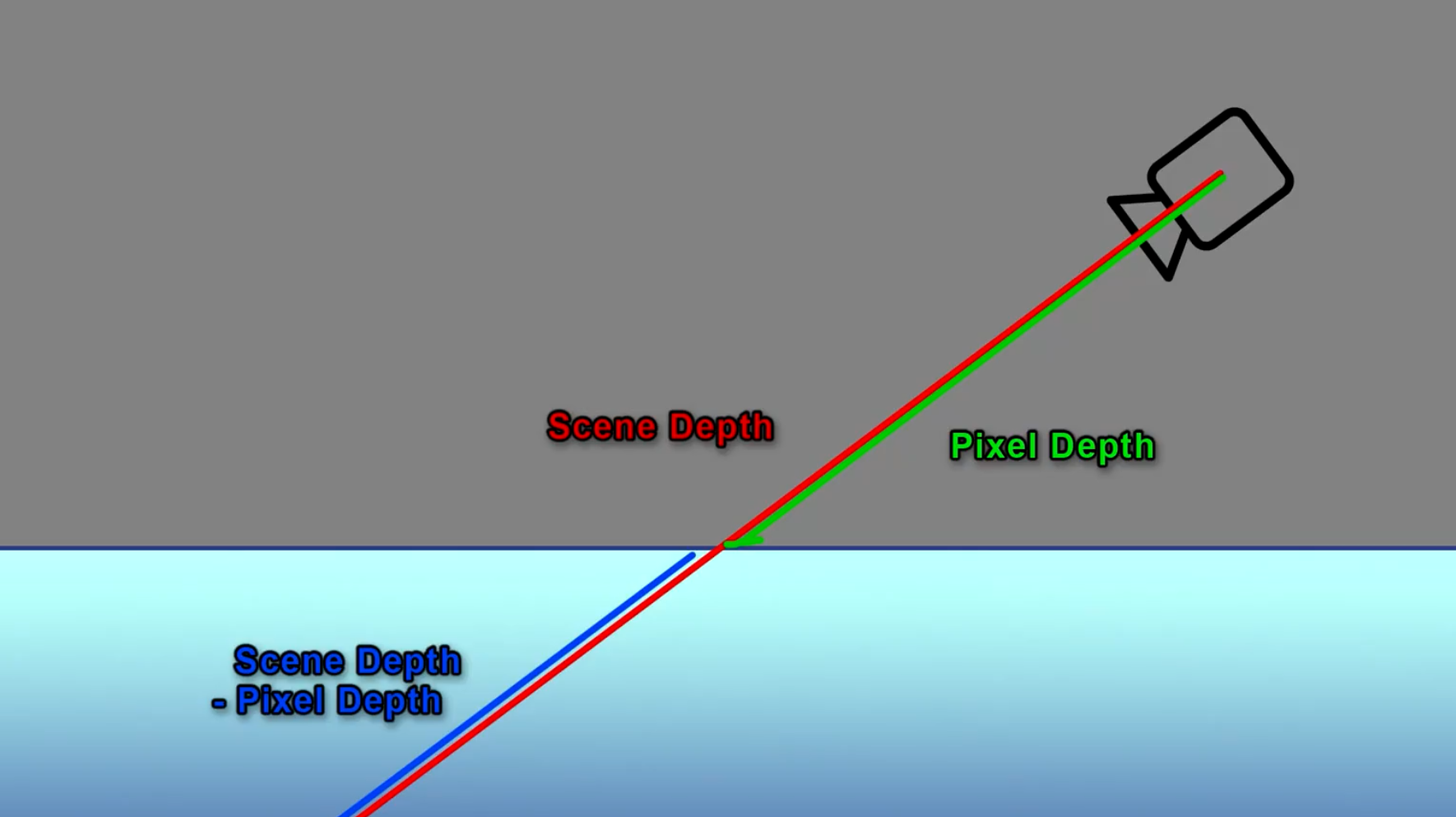
实现
-
初步实现
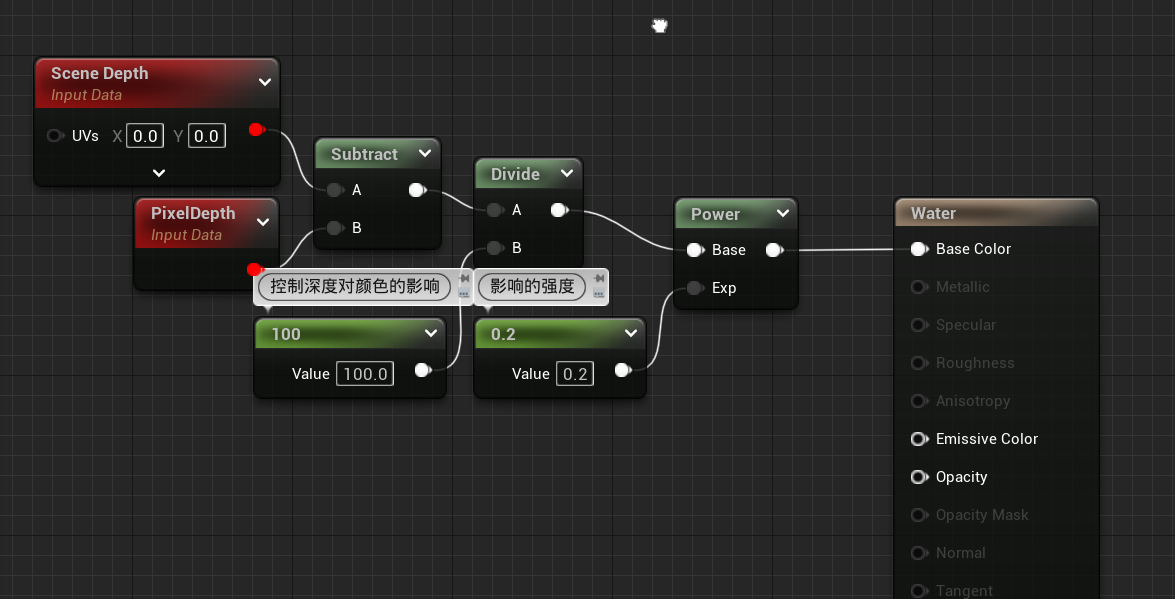

从上图可以看出这正是我们想要的效果,从浅到深,刚开始有些黑色,然后变白
-
纠正视角问题
-
问题
当我们垂直看去,得到的效果如下

当我们水平看去,得到的效果如下

可以看出因为角度的问题,求得的深度值也有所不同,角度越偏向水平,得到的深度值越大,透明度越低
-
原因
很明显水深并不是"SceneDepth - PixelDepth",而是垂直的深度,这里用相似即可实现
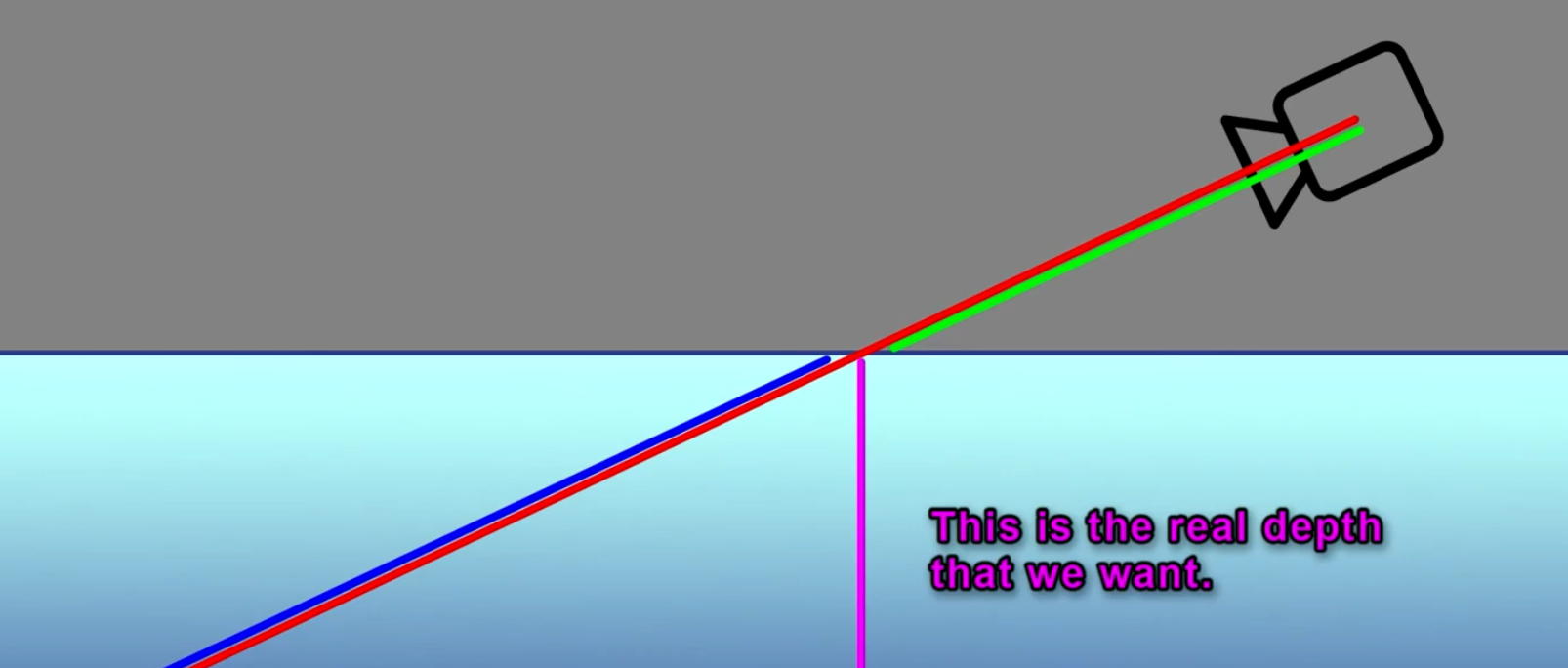
-
实现



-
测量角度
目标
- 当视角越来越垂直水面,水越来越透明
- 当视角越来越平行水面,水越来越不透明
实现
-
初步实现
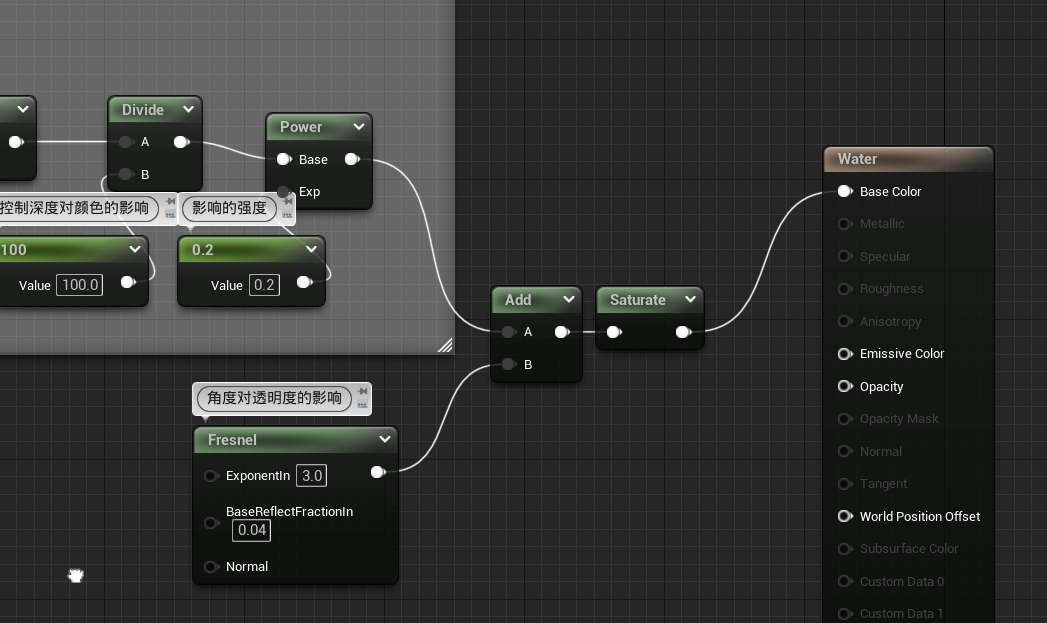


-
添加Normal,更改光照
将光照改为"Surface TranslucencyVolume"
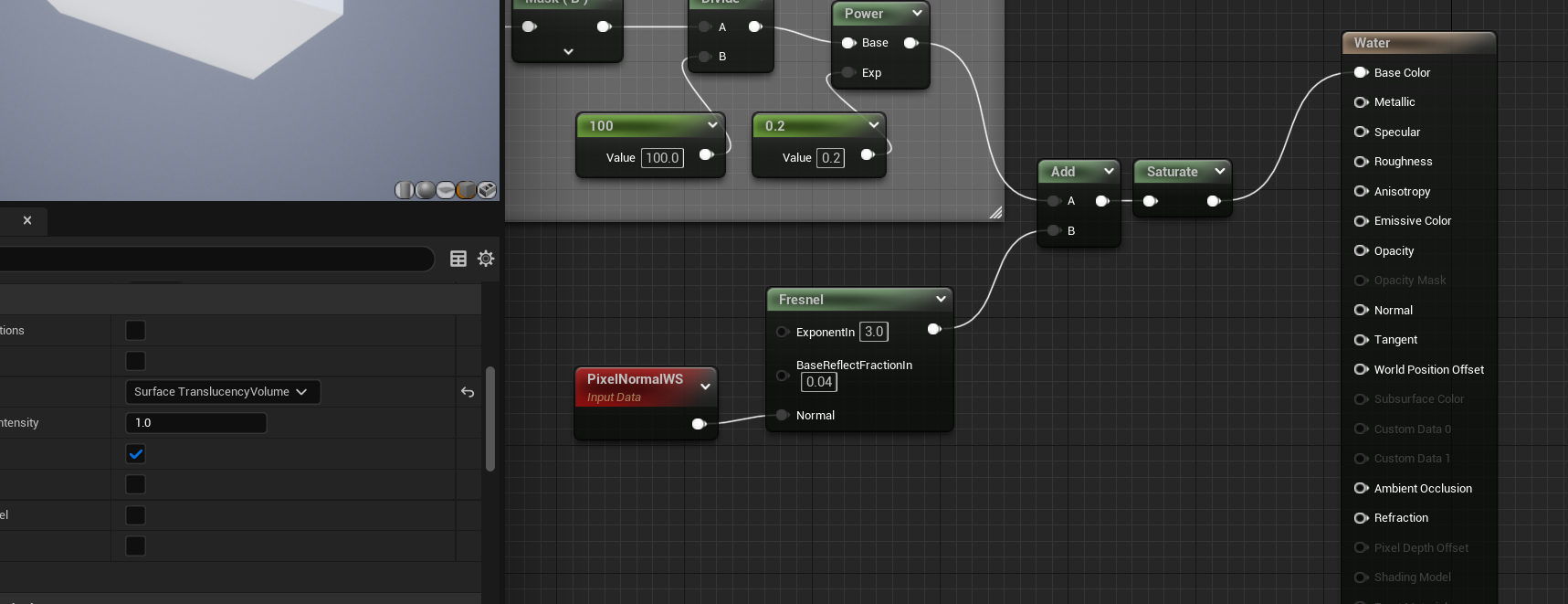
-
减弱水和物体交界的硬线
DepthFade的原理不懂的可以看这UE5 材质 基础知识 - 爱莉希雅 - 博客园 (cnblogs.com)
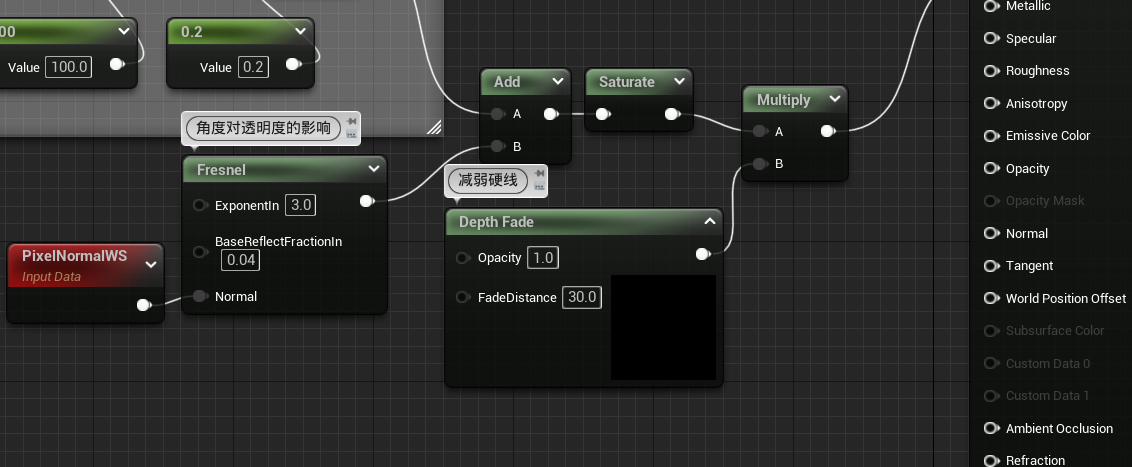

水颜色的渐变
目标
- 因为水的颜色收到深度的影响,因此我们需要创建两种颜色的水,一种代表深处的颜色,一种代表浅处的颜色
实现
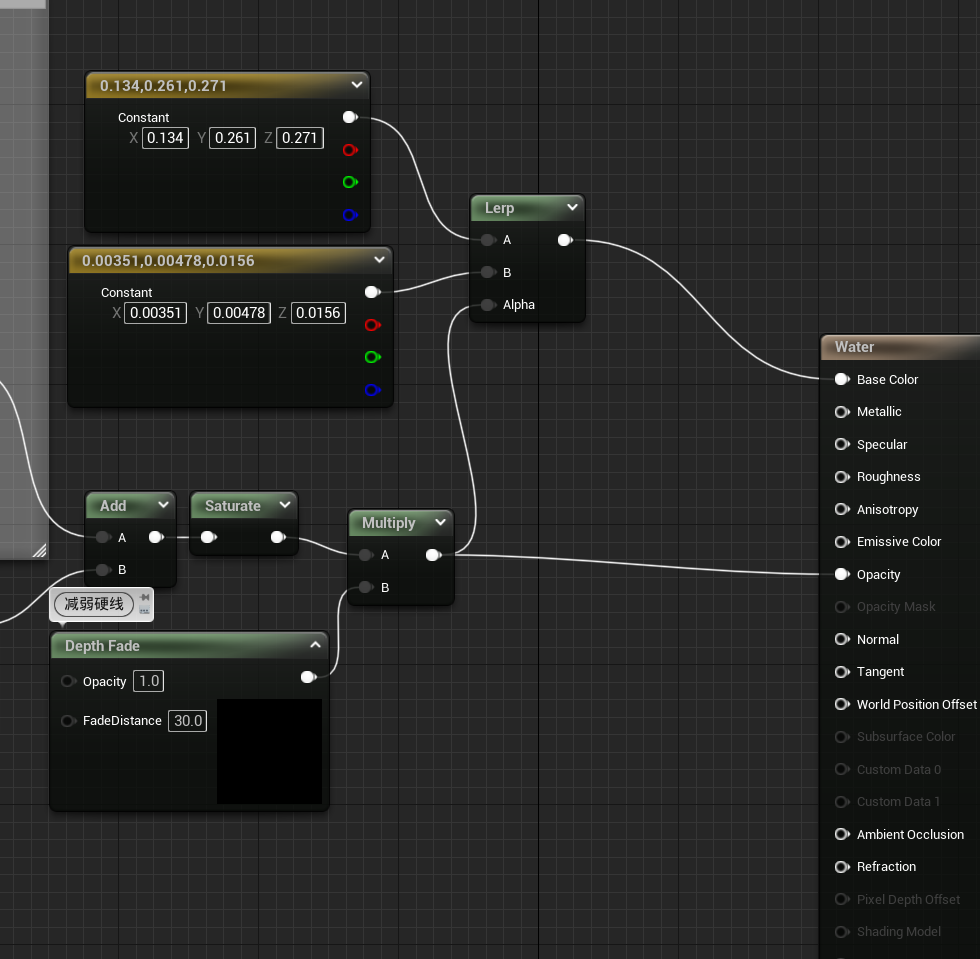

以下是水深的全部实现内容
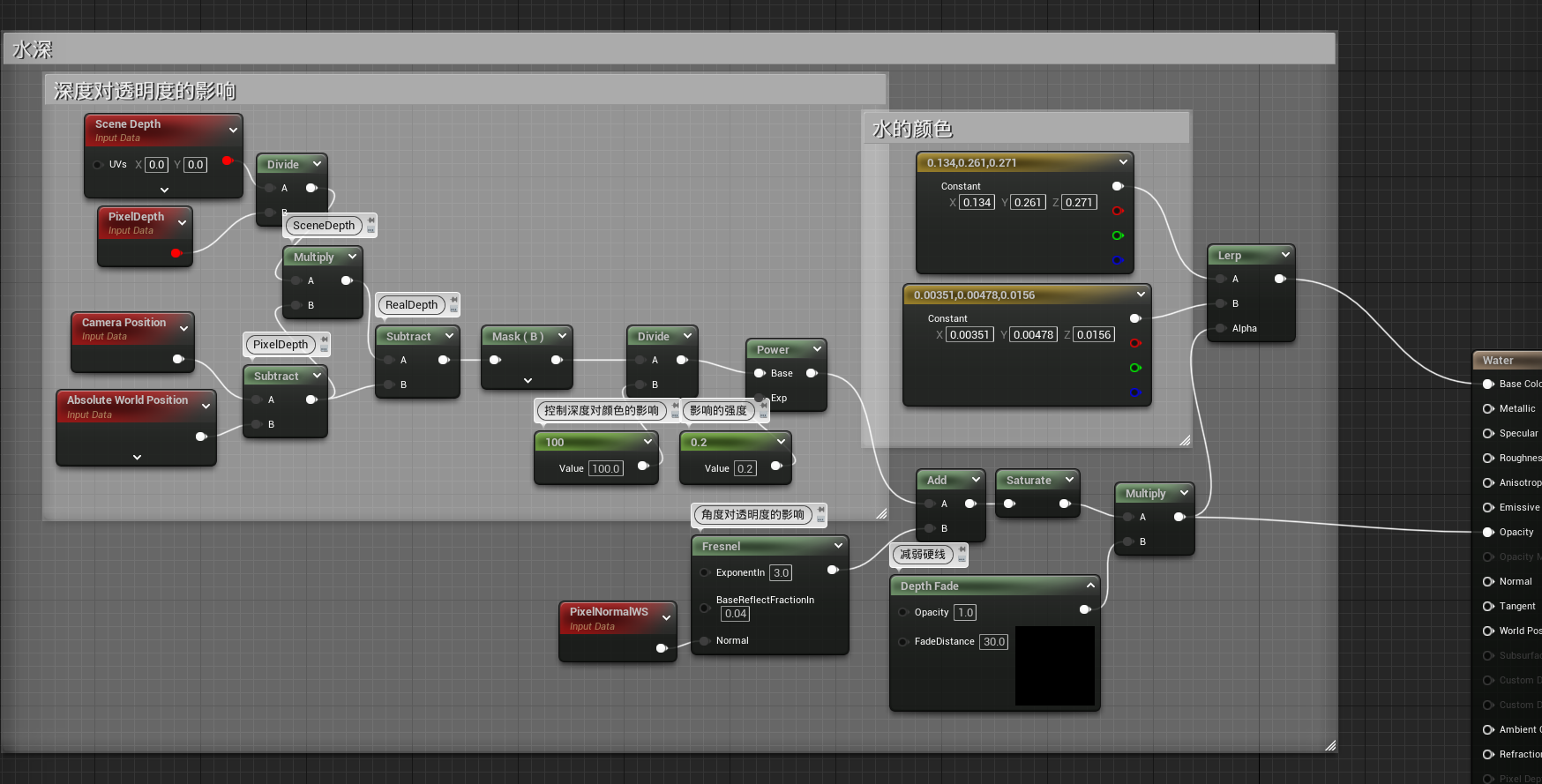
水的反射和折射
UE中的反射
-
UE中的反射有五种不同的实现方法,且许多场景不单单使用一种反射而是多种反射方法相结合。在这里我们介绍其中三种
-
sky box
通过sky box可以反射天空,但是它无法反射场景的物体。
-
Light Probe(光照探针)
Light Probe可以解决sky box的缺点。简单来说,Light Probe给予场景中某个点向它周围收集光照的能力,并记录周围的光照(irradiance map),也就是cubemap。随后对某个像素点进行渲染时,利用它附近的probe的光照信息估计该点所受光照

- 缺点
- 只适用于静态物体和静态光照。因为只是从Light Probe那个点来说光照是正确的,但如果从其他方向看去会发现反射是错误的
- 缺点
-
屏幕空间反射(Screen Space Reflections)
简单来说,Screen Space Reflections以屏幕数据计算反射效果。因为它需要G-Buffer中的normal,所以只适用于延迟渲染
- 缺点
- 成本高
- 只能反射屏幕内的物体,对屏幕外的无效
- 缺点
-
UE中的折射
-
UE5提供了两种折射模式,一种是基于物理的无normalmap的折射模式"Index of Refraction";另一种是不基于物理的normal的折射模式"Pixel Normal Offset"
-
这两种模式各有长处
-
Index of Refraction模拟光线在介质间传播时的折射方式。适用于小物体,对于较大的物体很可能会带有瑕疵,因为当前屏幕中的物体的颜色很可能从屏幕外获取
-
Pixel Normal Offset以vertex normal为基础,计算每个pixel的normal和vertex normal的差异来得出折射偏移。适用于较大平面,因为无需从屏幕外读取数据。需要注意的是,若参数"Refraction Depth Bias" > 1,法线将沿平面平移
-
参数Refraction Depth Bias
Refraction Depth Bias用于防止距离较近的对象以尖锐的(acute)视角渲染到扭曲的表面。但可能会增加表面和折射位置的距离
-
-
启用反射和折射
- 在根节点处启用"Screen Space Reflections"
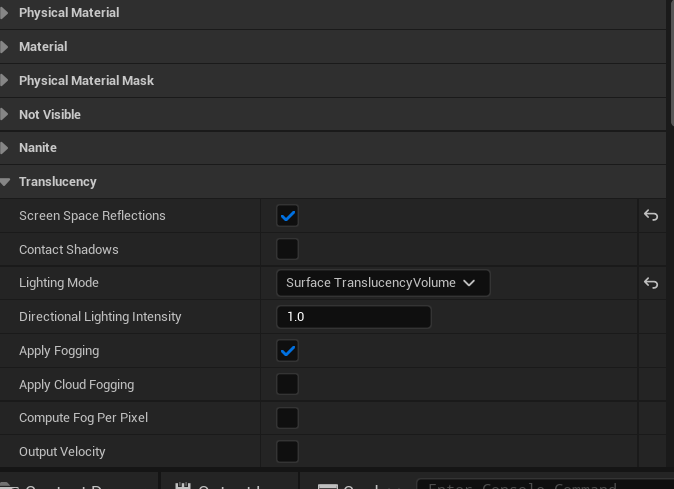
- 在根节点处选用"pixel normal offset"
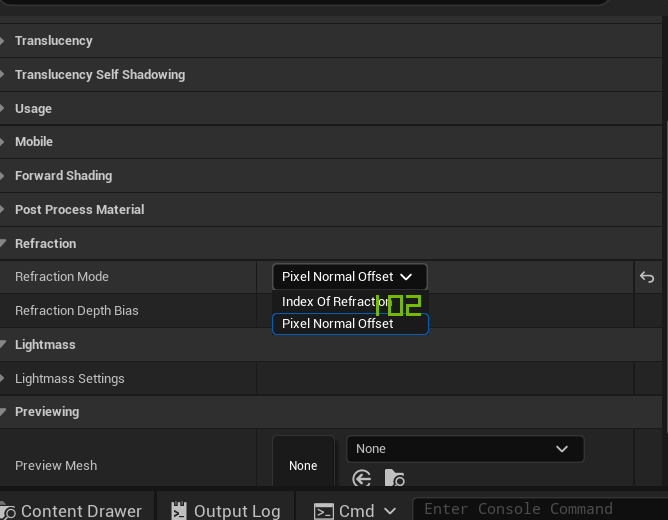
- 效果
- 没有开启折射

- 开启折射

- 没有开启折射
海浪
海浪算法
思想
- 水体渲染主要运用两个表面的模拟:一个用于表面网格的几何波动,另一个是网格上法线图的扰动。而水面高度由简单的周期波叠加表示
- 因为水的波纹呈sin分布,所以我们基于简单的sin函数进行叠加可以得到一个连续函数,该函数描述水面上所有点的高度和方向
波的选择
- 在正式开始前,我们需要了解不同类型的波浪应该用哪种波形
- 对于受风影响生成的波,应使用方向波。对于方向波,波的方向是在风的一定范围内画的
- 对于平静的水面,生成的波并不是因为风(如瀑布),应使用圆形波。对于圆形波,波中心是在限定范围内任意画的
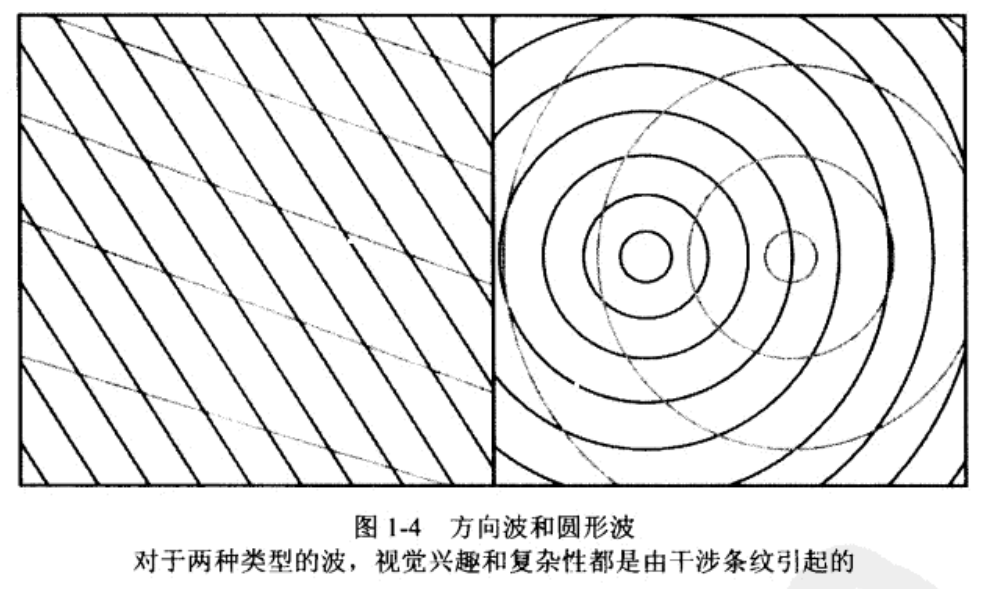
为什么选择Gerstner算法?
- 因为Gerstner算法有一个特性,它将顶点朝着每个浪头顶部移动,从而形成更尖锐的波峰。而这一特性,正是我们所需要的
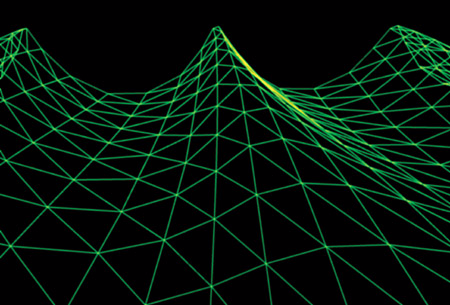
从sin函数开始
- 由于sin函数在x轴方向不变,在y轴方向上下移动,使得它形成的面更为圆滑,因此sin函数更适合平静的湖面
参数选择
-
对于波的形成,我们需要考虑以下几个参数
- 波长(\(L\)):world space中波峰到波峰的间距。\(L\)和\(\omega\)(角频率)的关系 \(\omega = \frac{2\pi}{L}\)
- 振幅(A):水平面到波峰的间距
- 速度(S):波峰每秒移动的距离。为方便将S表示为相位常数\(\varphi = S \frac{2\pi}{L}\)
- 方向(D):垂直于波面且的水平向量
-
波的状态定义为位置(x,y)和时间t的函数:\(W_i(x,y,t) = A_i \times sin(D_i · (x,y) \times \omega_i + t \times \varphi_i)\)
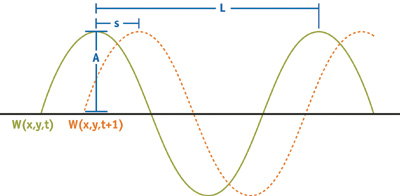
-
所有波i的总表面:\(W_i(x,y,t) = \sum A_i \times sin(D_i · (x,y) \times \omega_i + t \times \varphi_i)\)
法线和切线
- 切线和副切线分别是y方向和x方向上的偏导
- 现有2d平面的任意点\((x,y)\),表面的3d坐标\(p(x,y,t) = (x,y,H(x,y,t))\)
- 切线即为对y轴求偏导:\(T(x,y) = (0, 1, \frac{\partial}{\partial y}(H(x,y,t))\)
- 副切线即为对x轴求偏导:\(B(x,y) = (1, 0, \frac{\partial}{\partial x}(H(x,y,t)))\)
- 法线即为副切线和切线的叉乘:\(N(x,y) = (-\frac{\partial}{\partial x}(H(x,y,t)), -\frac{\partial}{\partial y}(H(x,y,t), 1)\)
Gerstner波
- Gerstner波有一个特性,它将顶点朝着每个浪头顶部移动,从而形成更尖锐的波峰,这适用于粗犷的海洋
- Gerstner波中每一个水分子都在做圆周运动,这意味着x,y都在变化(而sin函数只有y变化,x不变),且水分子在波峰聚集,在波谷分散,越靠近水面,圆周运动的半径越大
定义
-
Gerstner波定义
\(P(x,y,t) = \left(\begin{array}{cc} x + \sum(Q_i A_i \times D_i.x \times cos(\omega_i D_i·(x,y) + \varphi_i t)) \\ y + \sum(Q_iA_i \times D_i.y \times cos(\omega_i D_i·(x,y) + \varphi_i t)) \\ \sum(A_i sin(\omega_i D_i·(x,y) + \varphi_i t)) \end{array}\right)\),其中\(Q_i = \frac{1}{\omega_i A_i}\)
-
对于单个波i,当\(Q_i = 0\)时,Gerstner波为sin波
- 使用\(Q_i = \frac{Q}{\omega_i A_i \times numWaves}\)可以控制波的平滑或尖锐程度
- 需要注意的是,应当避免使用过大的\(Q_i\),这会导致波峰形成环

切线和法线
- 副切线\(B = \left(\begin{array}{cc} 1-\sum(Q_i \times D_i.x^2 \times WA \times S()) \\ -\sum(Q_i \times D_i.x \times D_i.y \times WA \times S()) \\ \sum(D_i.x \times WA \times C()) \end {array}\right)\)
- 切线\(T = \left(\begin{array}{cc} -\sum(Q_i \times D_i.x \times D_i.y \times WA \times S()) \\ 1 - \sum(Q_i \times D_i.y^2 \times WA \times S()) \\ \sum(D_i.y \times WA \times C()) \end{array}\right)\)
- 法线\(N = \left(\begin {array}{cc} -\sum(D_i.x \times WA \times C()) \\ -\sum(D_i.y \times WA \times C()) \\ 1 - \sum(Q_i \times WA \times S()) \end{array}\right)\)
其中:- $ WA = \omega_i \times A_i $
- $ S() = sin(\omega_i \times D_i · P + \varphi_i t) $
- $ C() = cos(\omega_i \times D_i · P + \varphi_i t) $
参数
-
波长
这里波长的选择不是根据现实而定,而是使用少数几个波达到最大效果。因此我们选择中等的波长,以它的\(\frac{1}{2}\)到\(2\)倍间产生任意波长
-
波速
波速与波长L、重力g(国际单位\(9.8m/s^2\))相关:\(S = \sqrt{g \times \frac{2\pi}{L}}\)
-
振幅
在Shader中指定一个系数,由美术人员对波长指定对应的合适振幅
-
方向
波的运动方向和其他参数完全独立,可以自由选择
实现
-
解决水面交界的绿线

从上图可以看到水面和岩石及墙体的交界都有一道绿线,这是由"depth fade"节点造成的。"depth fade"在我们的实现中仅仅用于水的不透明度,但我们却将其用在水的颜色

-
降低水和物体交界处的折射效果以交界处的硬线

从上图可以看到在物体和水面的交界处折射效果十分强烈,但我们希望在交界处的折射效果不那么强烈。为了降低折射效果我们需要用到"depth fade"节点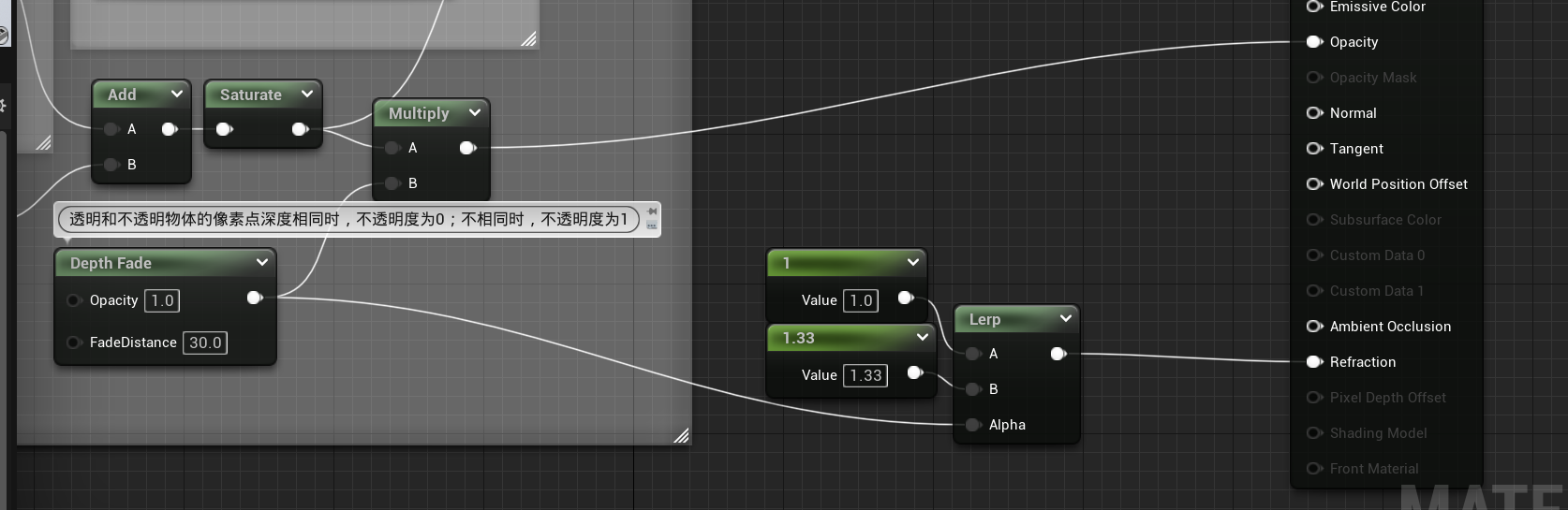

海浪
- 套用上述公式,可以轻易求得海浪的坐标变化和法线变化
-
坐标变化
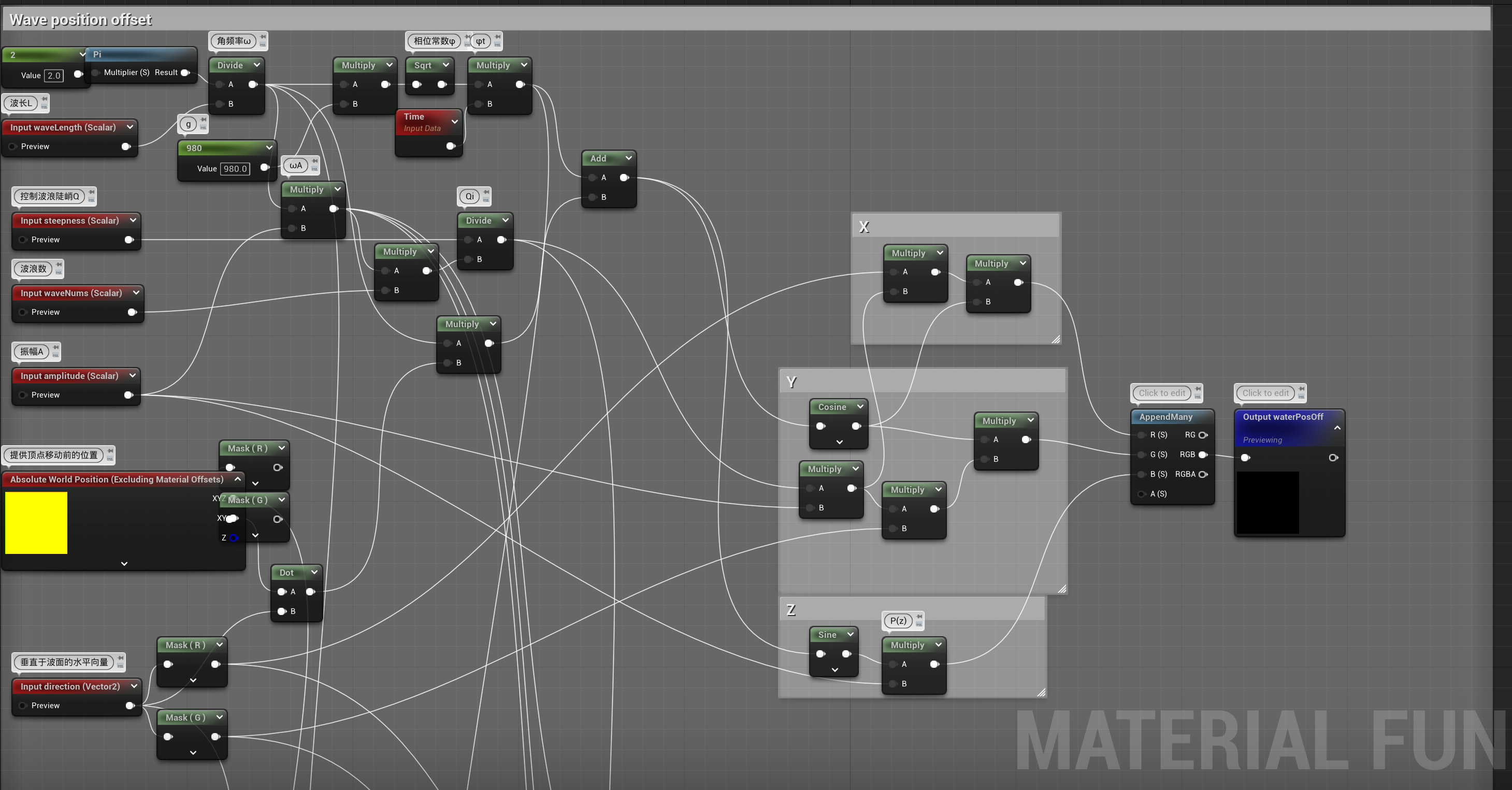

简单地改变海浪的尖锐程度、振幅和波长

-
法线变化
可以看到目前这个海浪更像波,因为我们并没有求得海浪的法线变化。
海浪的法线变化求取如下


-
- 叠加波
从上面几张图来看目前实现的海浪其实一直在重复,为了避免重复性需要对波进行叠加
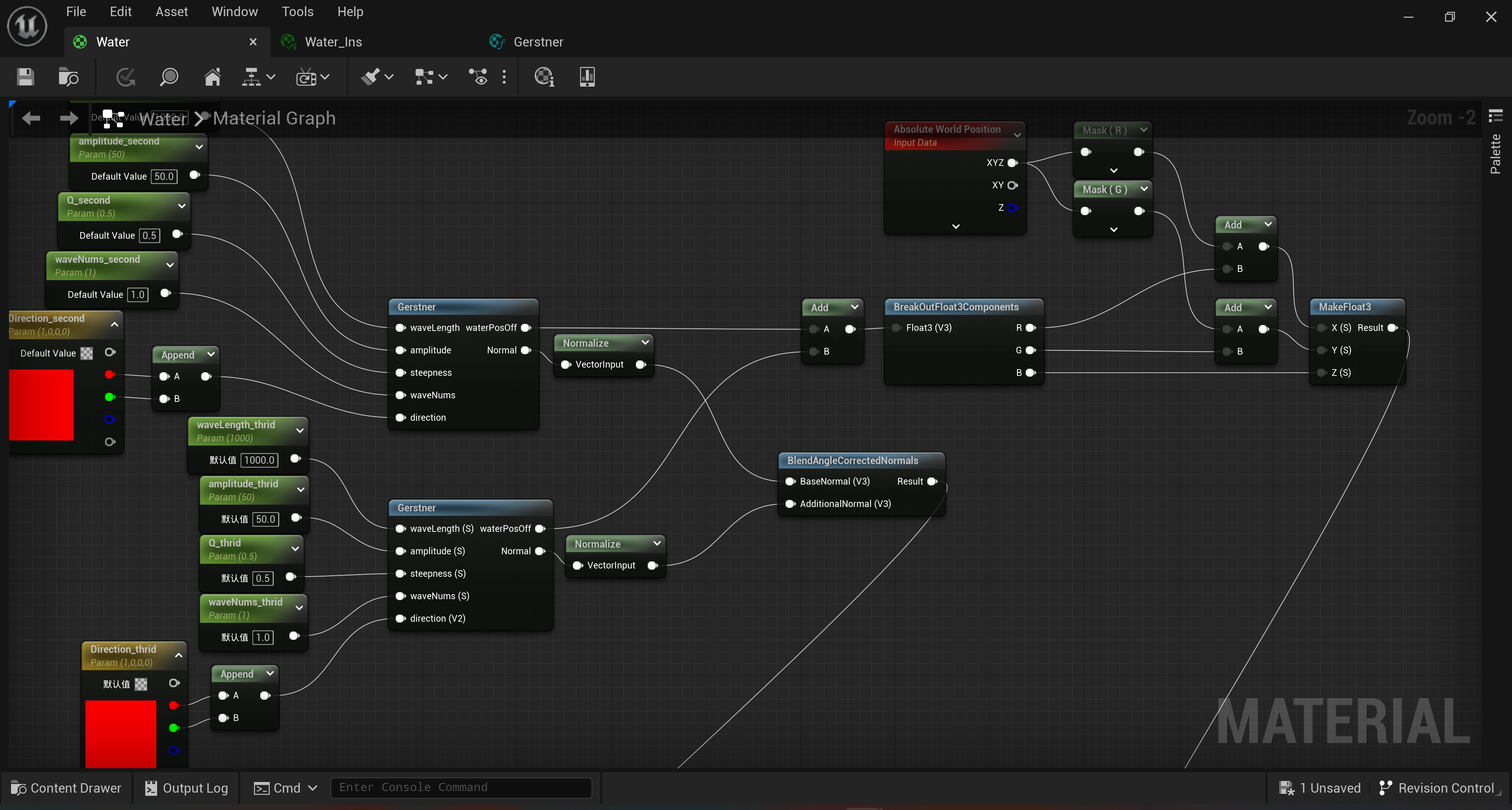
波光焦散
目标
- 在现实中,当太阳照射水面,水面会扭曲这些光纤从而生成特别酷炫的纹理

原理
-
对于这种纹理也是可以实现的,实现方式是贴花(decal)
简单来说,运用在实时渲染中的贴花技术是屏幕空间的延迟贴花——利用现有的G-Buffer,直接将贴花投射在物体表面
-
运作时间
写入G-Buffer后,屏幕空间的后处理前
-
与TBN类似,需要将世界空间转换到贴花空间,这样才能得到正确的贴花位置及其纹理。随后计算投影位置即可
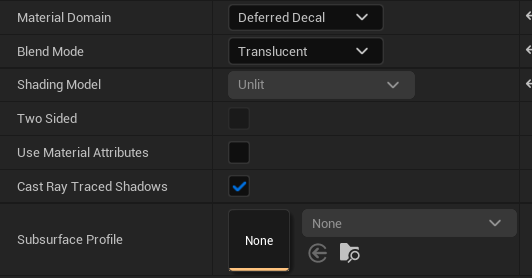
根节点设置
- 这里我们需要新建一个材质,并将根节点按如下设置
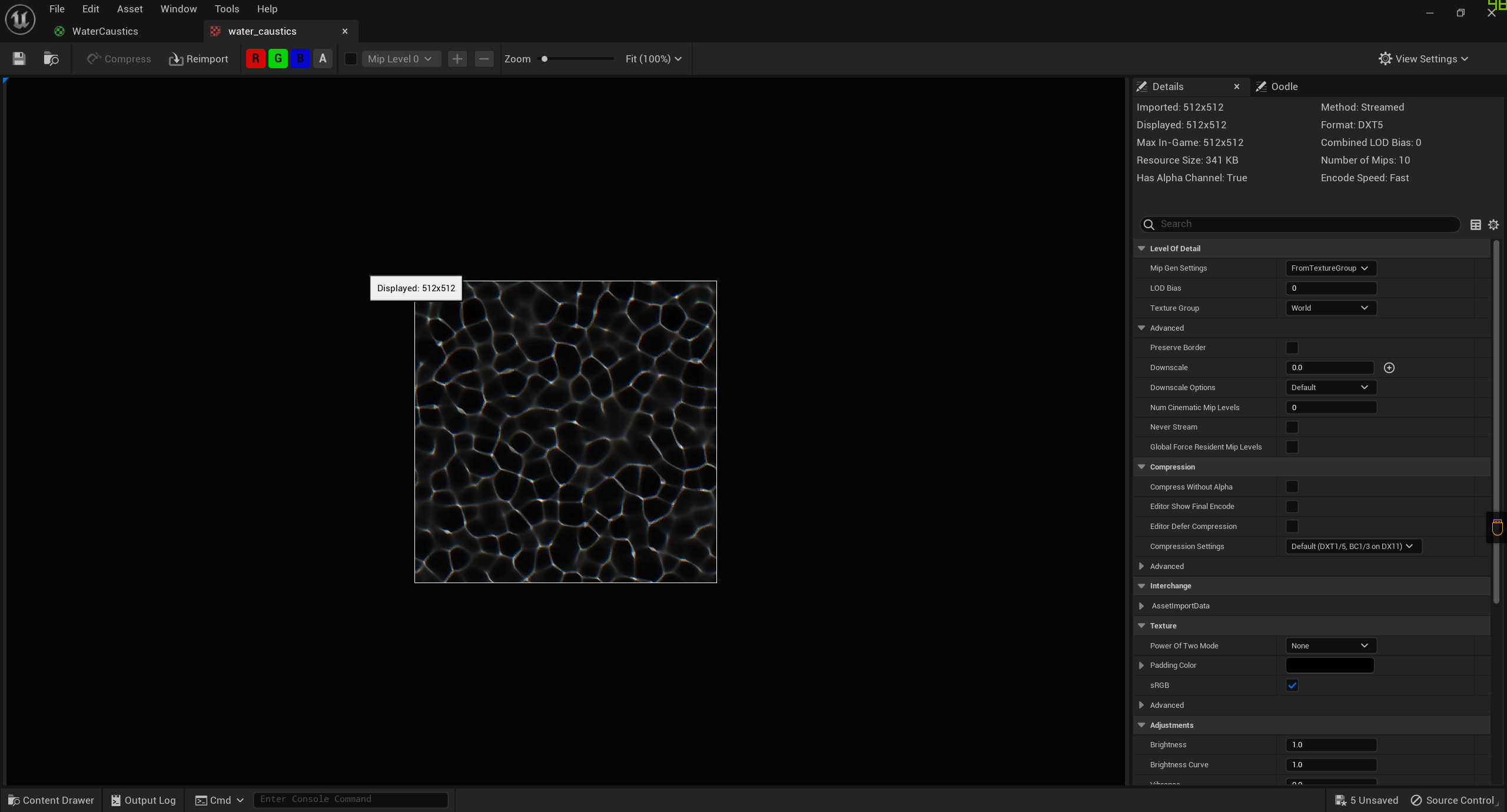
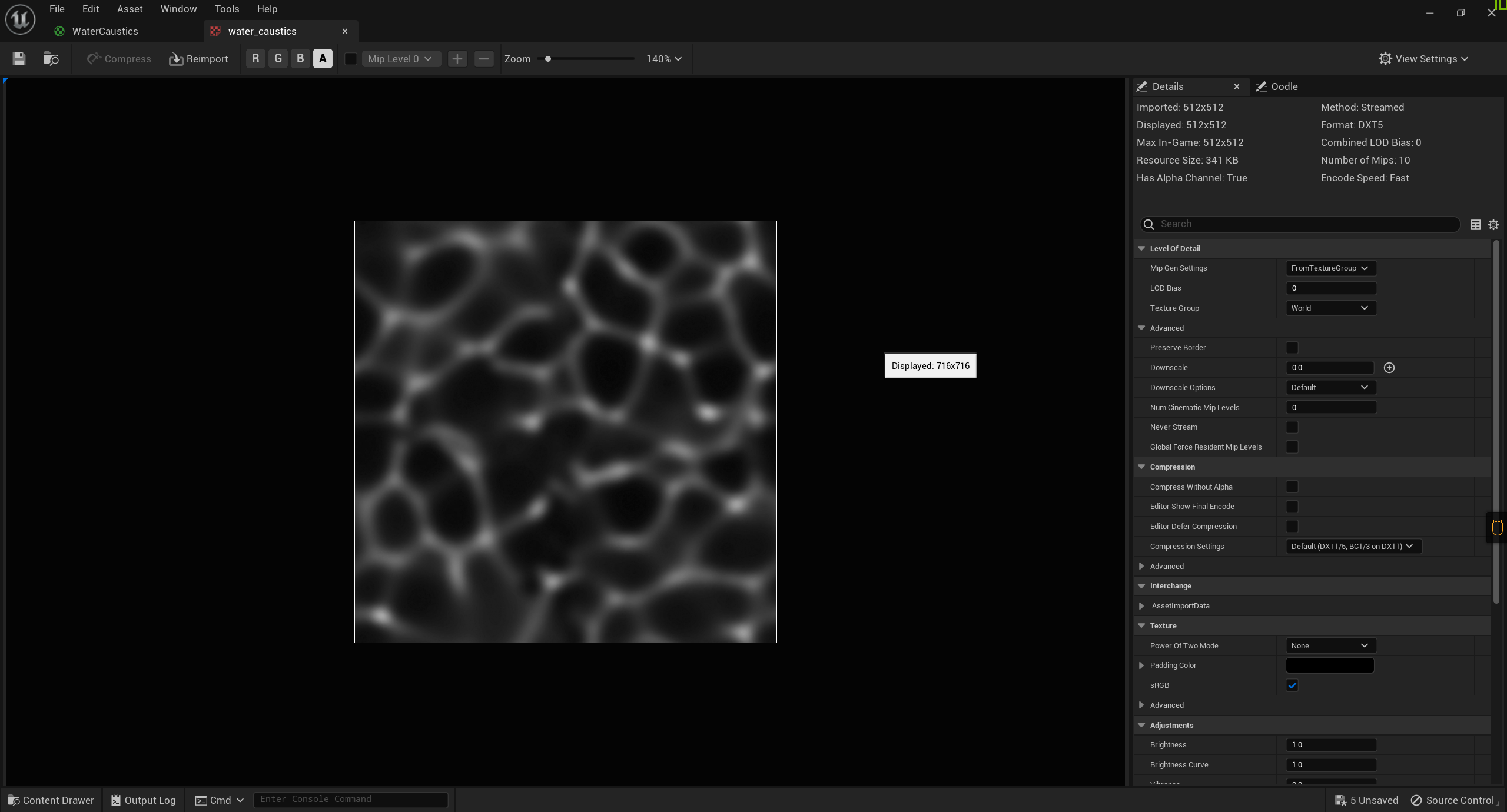
纹理
实现
初步实现
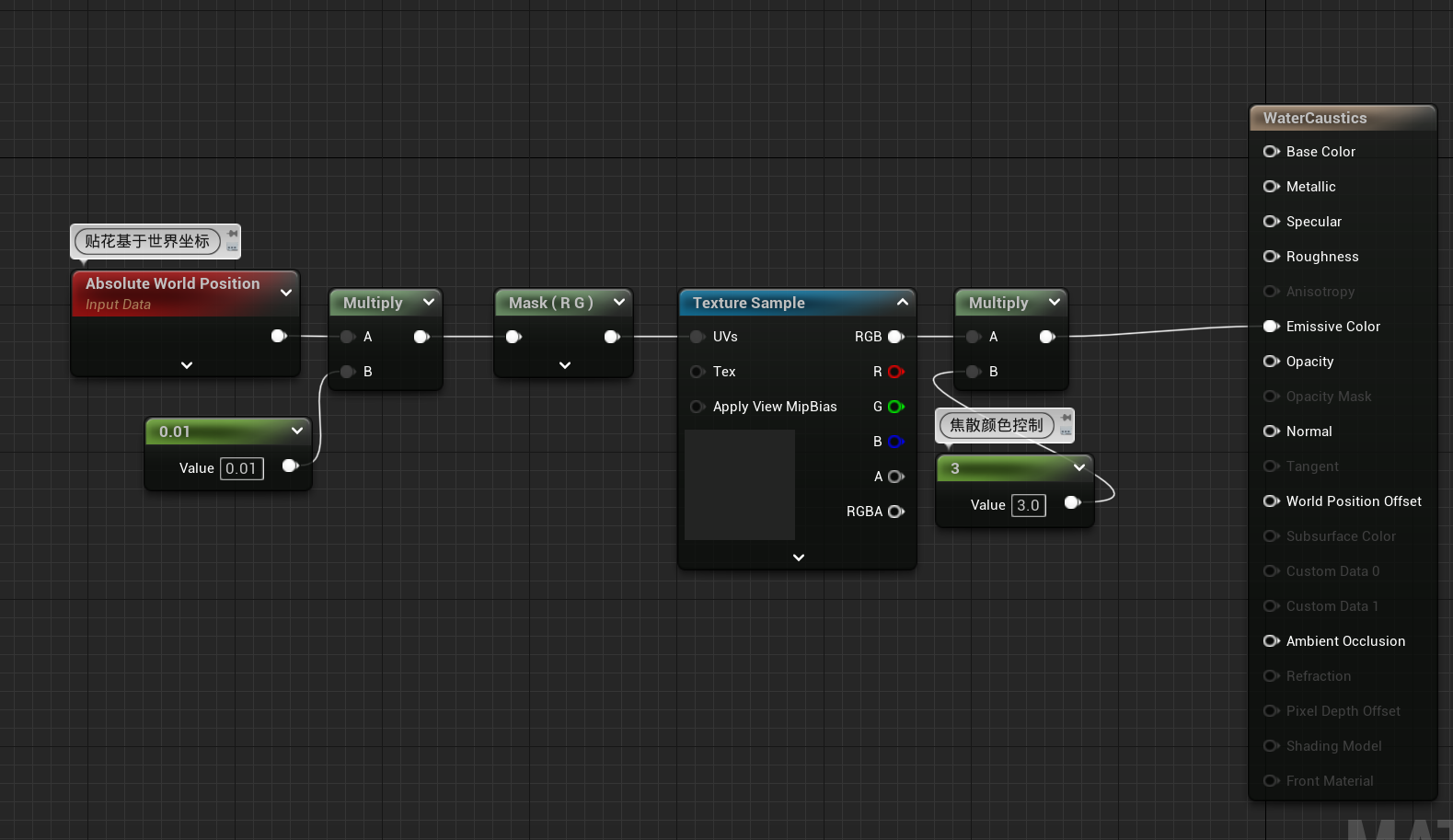
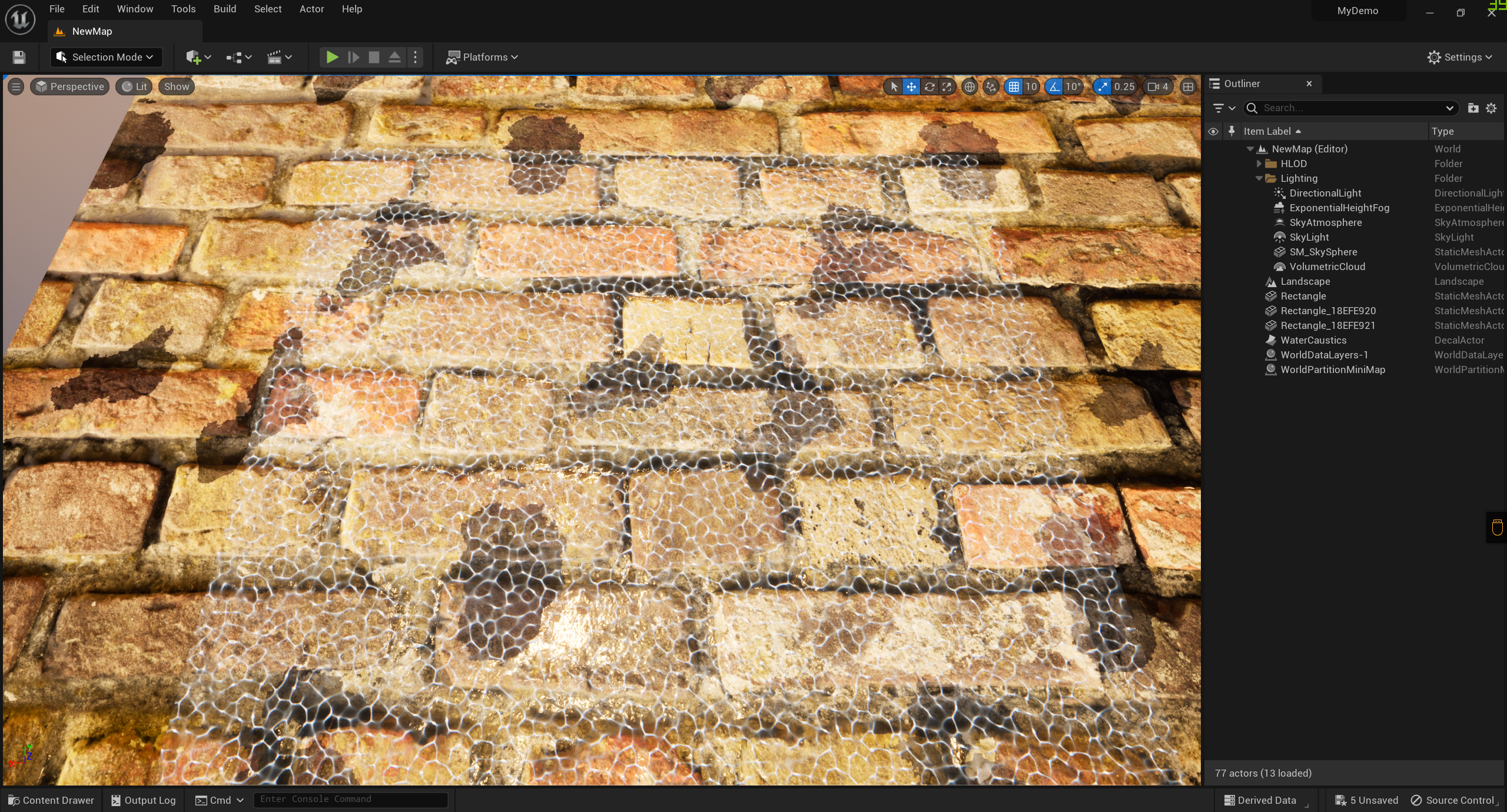
加入动画
-
简单的动画效果
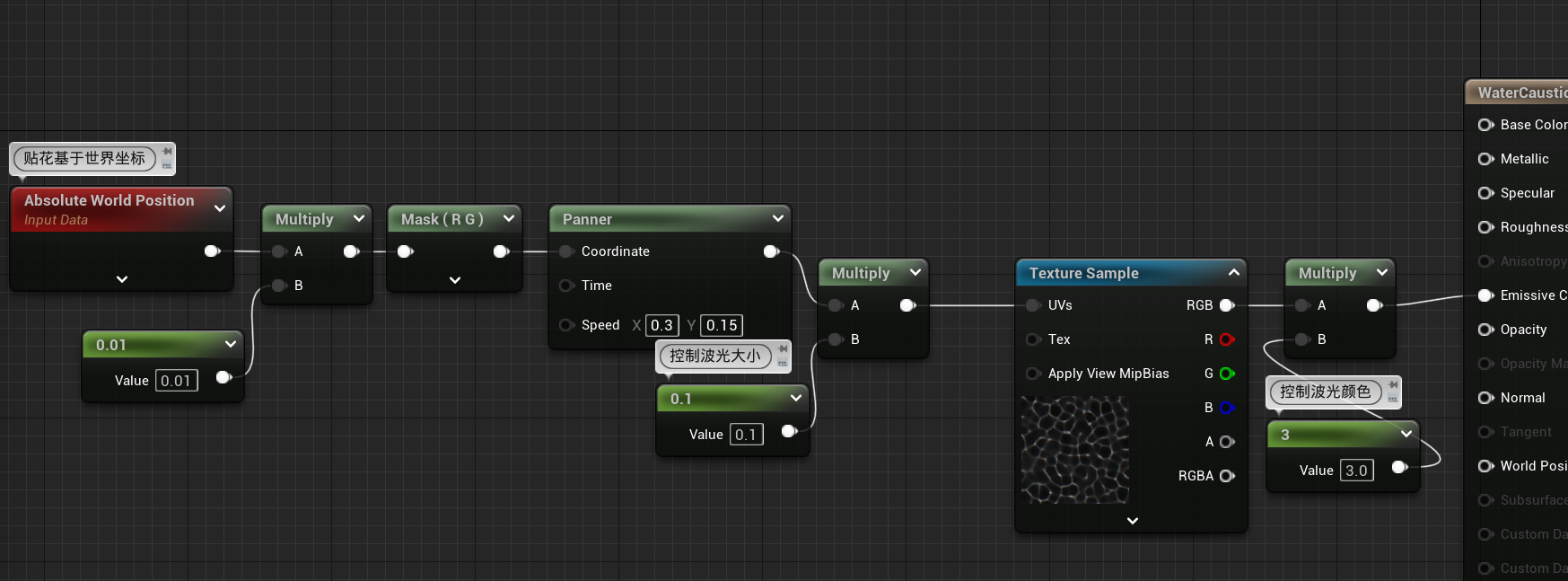

-
扭曲效果
目前的动画太有规律了,但现实中更像没有规律的。因此,我们需要将平移效果带点起伏
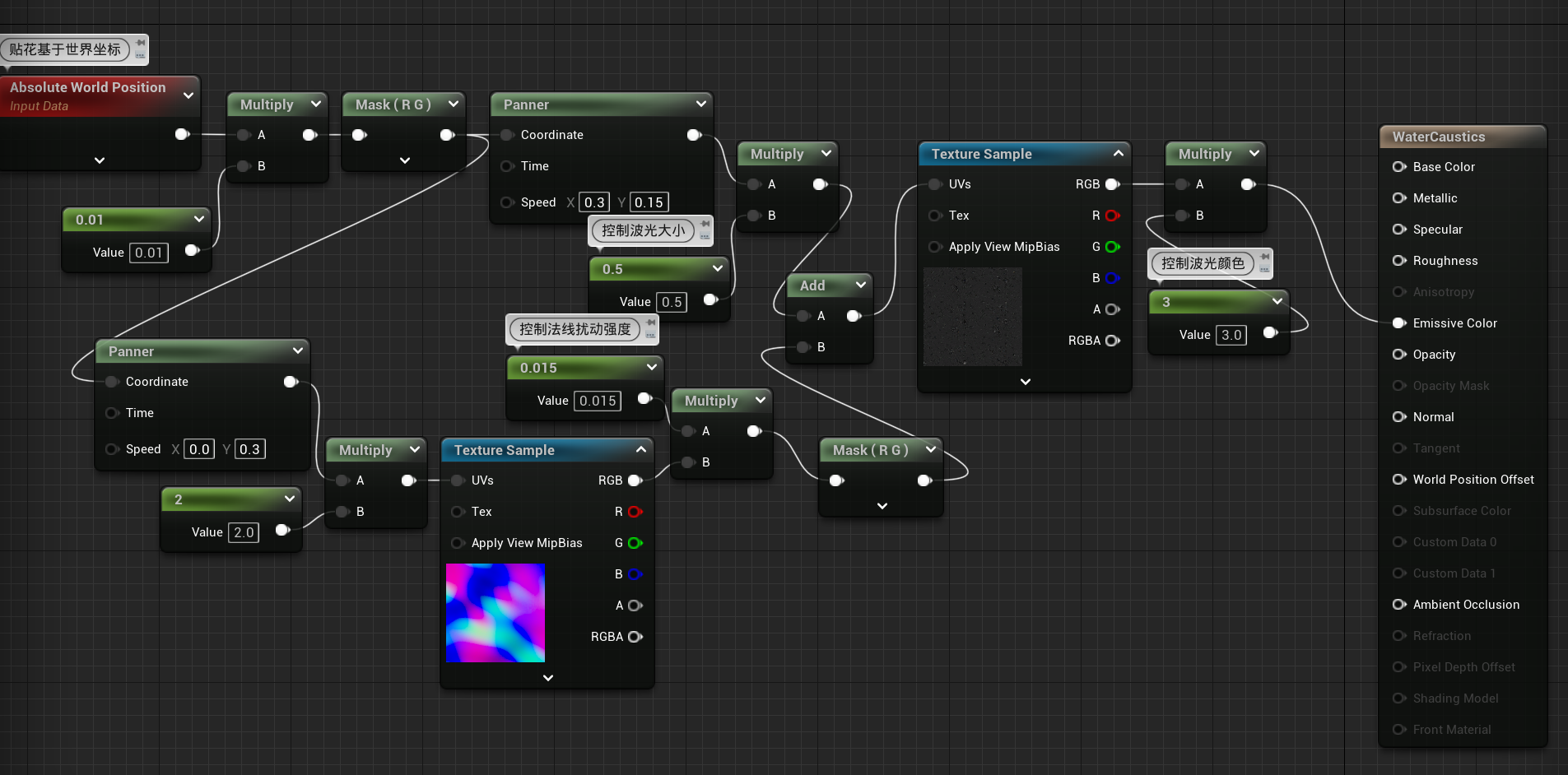

-
继续优化
可以看到确实有那味儿了!若为了更好的效果,可以再加一个不同的法线扰动效果
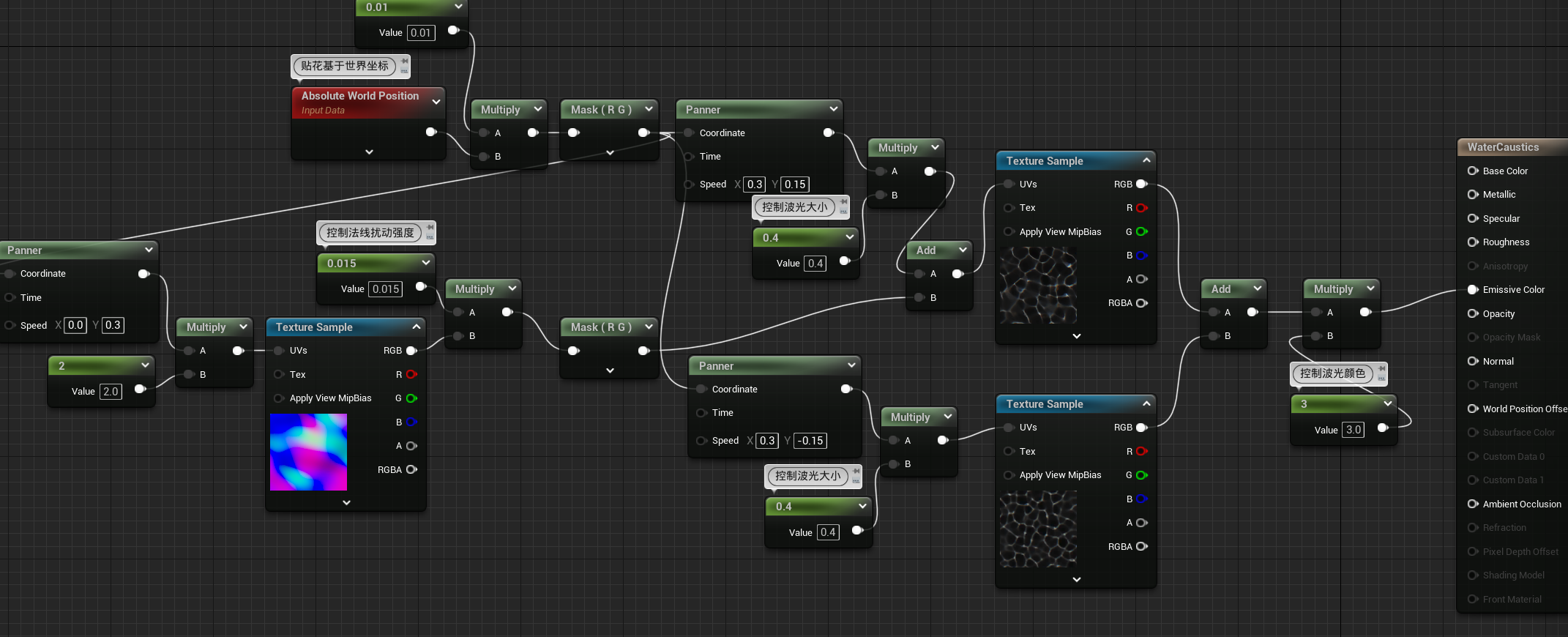

修正投影
- 目前,我们的贴花是基于z轴投影的,这会导致z轴的贴花不会有理想效果

- 如何修正呢?很简单,三个轴都进行投影
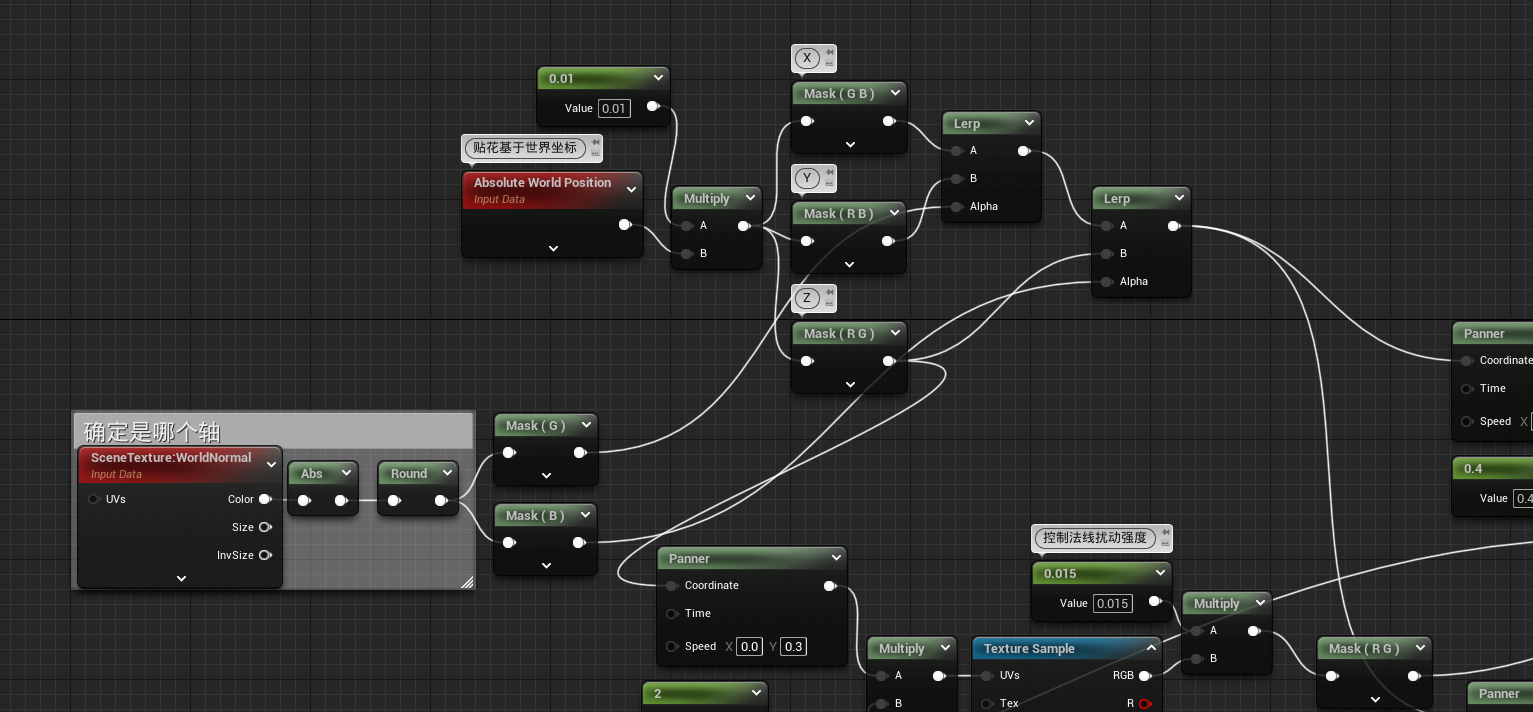

浪花
目标
实现当海浪和物体高速相撞时产生的浪花
纹理
浪花数量纹理
在这里使用到了一个纹理贴图
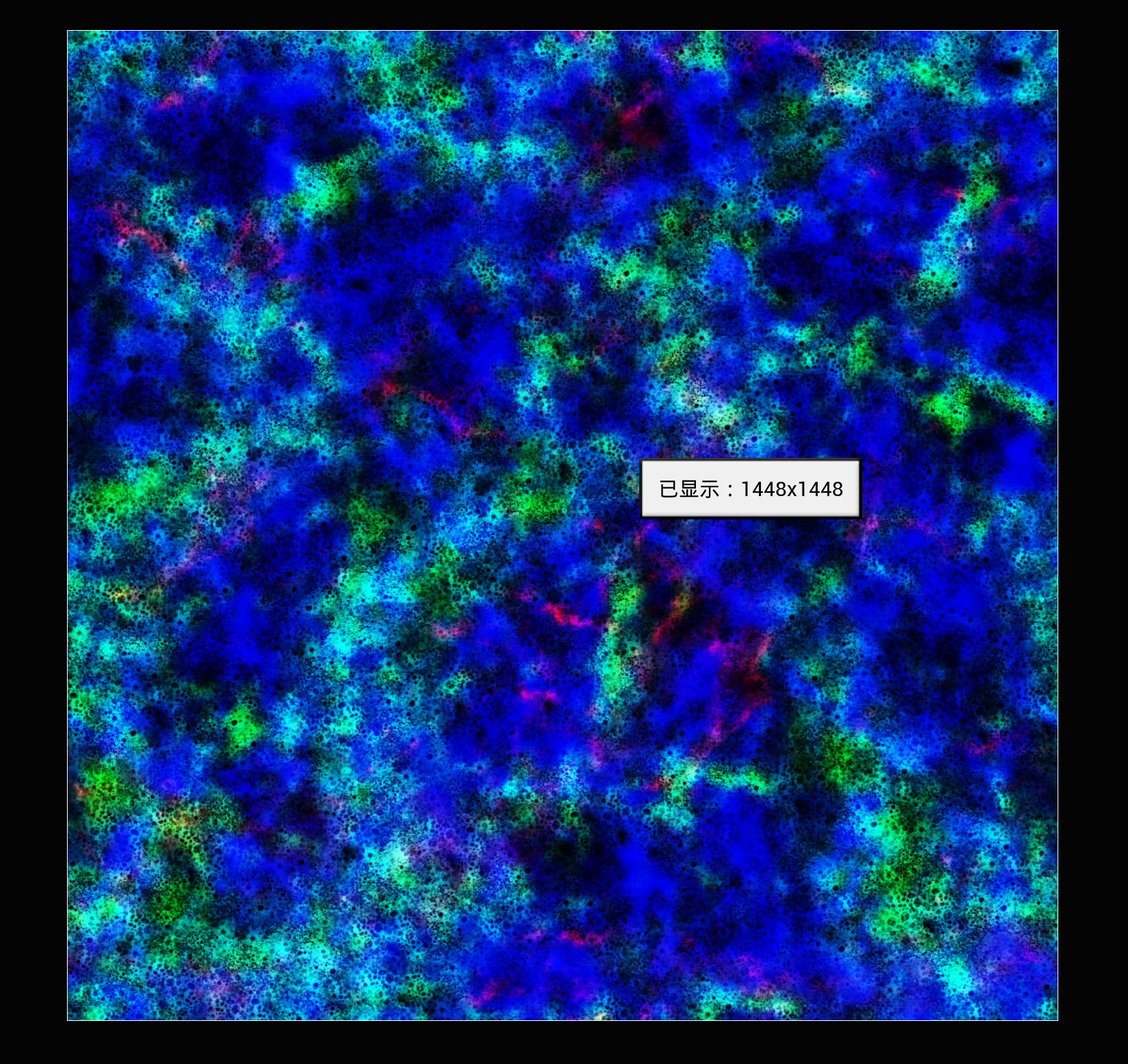
- R通道下
- G通道下
- B通道下
从上面三幅图可以看出这其实是代表三种浪花数量的贴图,这是因为浪花并不是一种分布均匀的物质,事实上是在一些区域可能会很厚,而在另一些区域很薄
浪花渐变纹理
因为浪花并不是一起出现,也不是一起消失的,所以需要一种纹理用于控制它的渐变
- R通道

- G通道

- B通道

显然的,这三个通道分别表示三种渐变程度
实现
motion_4waychaos函数
-
UE引擎提供了motion_4waychaos这一函数,但需要在"内容浏览器"中启用"显示引擎内容"
-
搜索"materialFunctionCall"
-
选中它继续搜索"motion_4waychaos"
-
函数的意义
简单来讲,该函数就是对纹理制造运动混乱
从实现不难看出该函数对同一纹理进行四次采样且四次uv都不相同,最后将他们相加
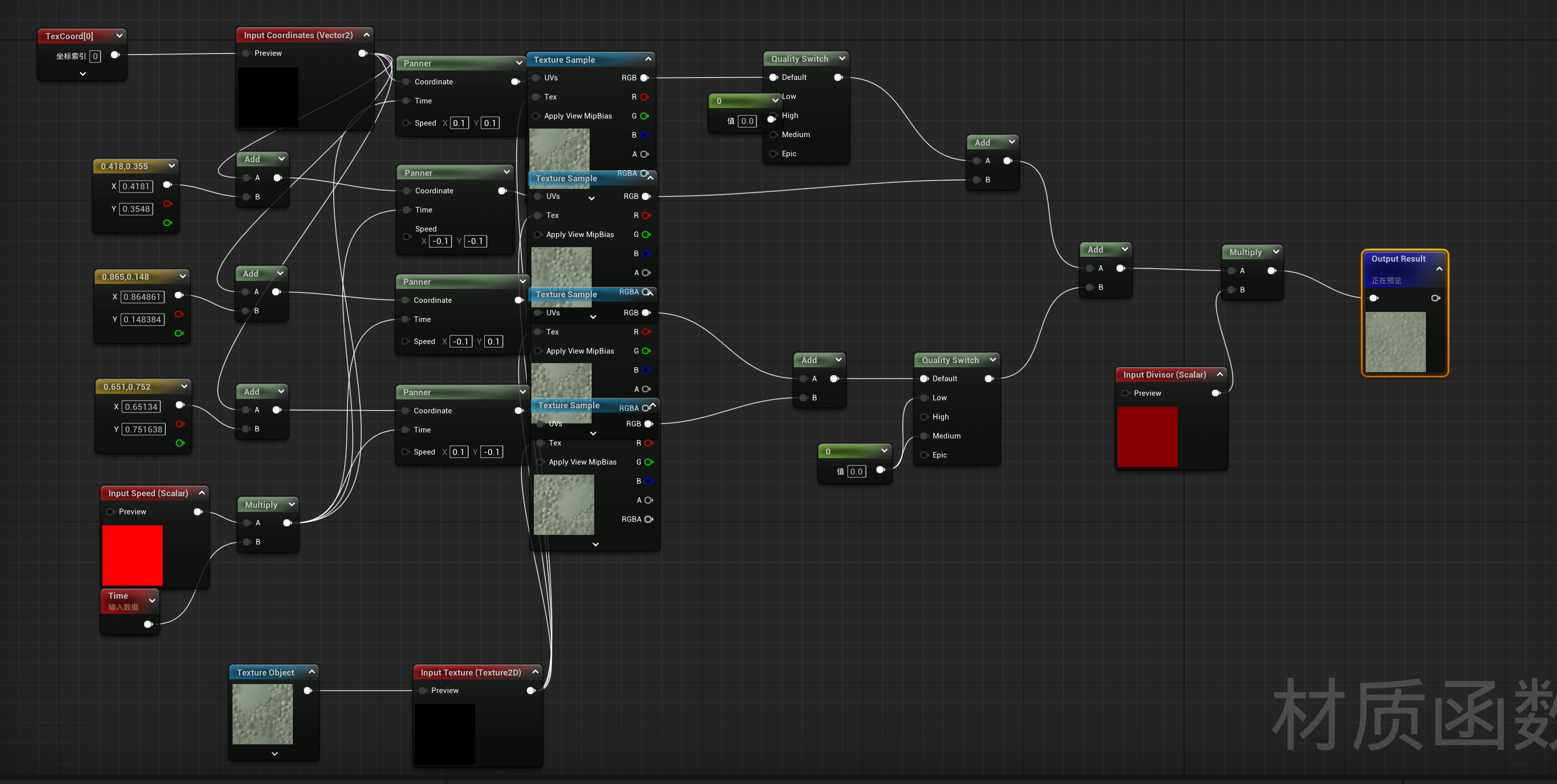
初步实现
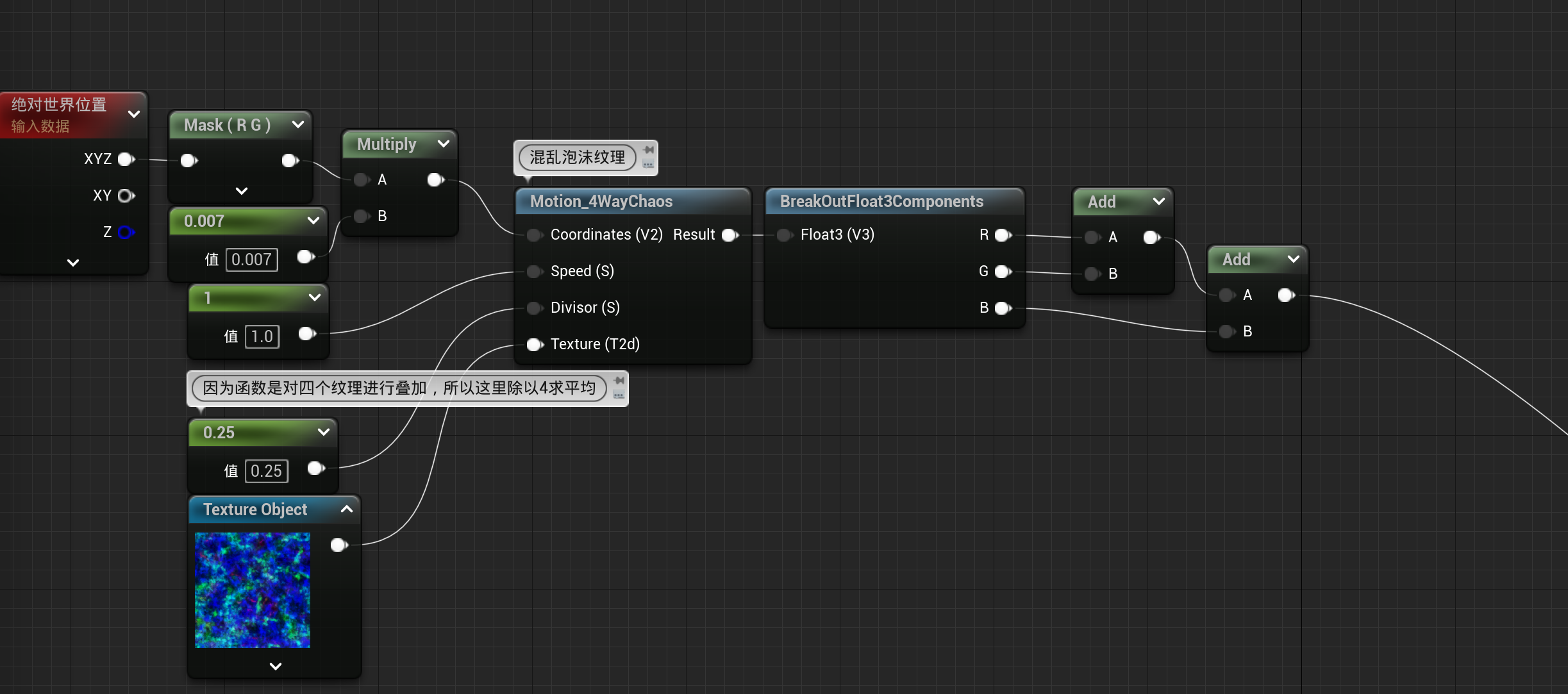

可以看到效果还不错有许多浪花
控制浪花出现的位置
-
设置寻址模式为clamp
这样可以防止渐变重复出现
-
以深度控制泡沫的多少
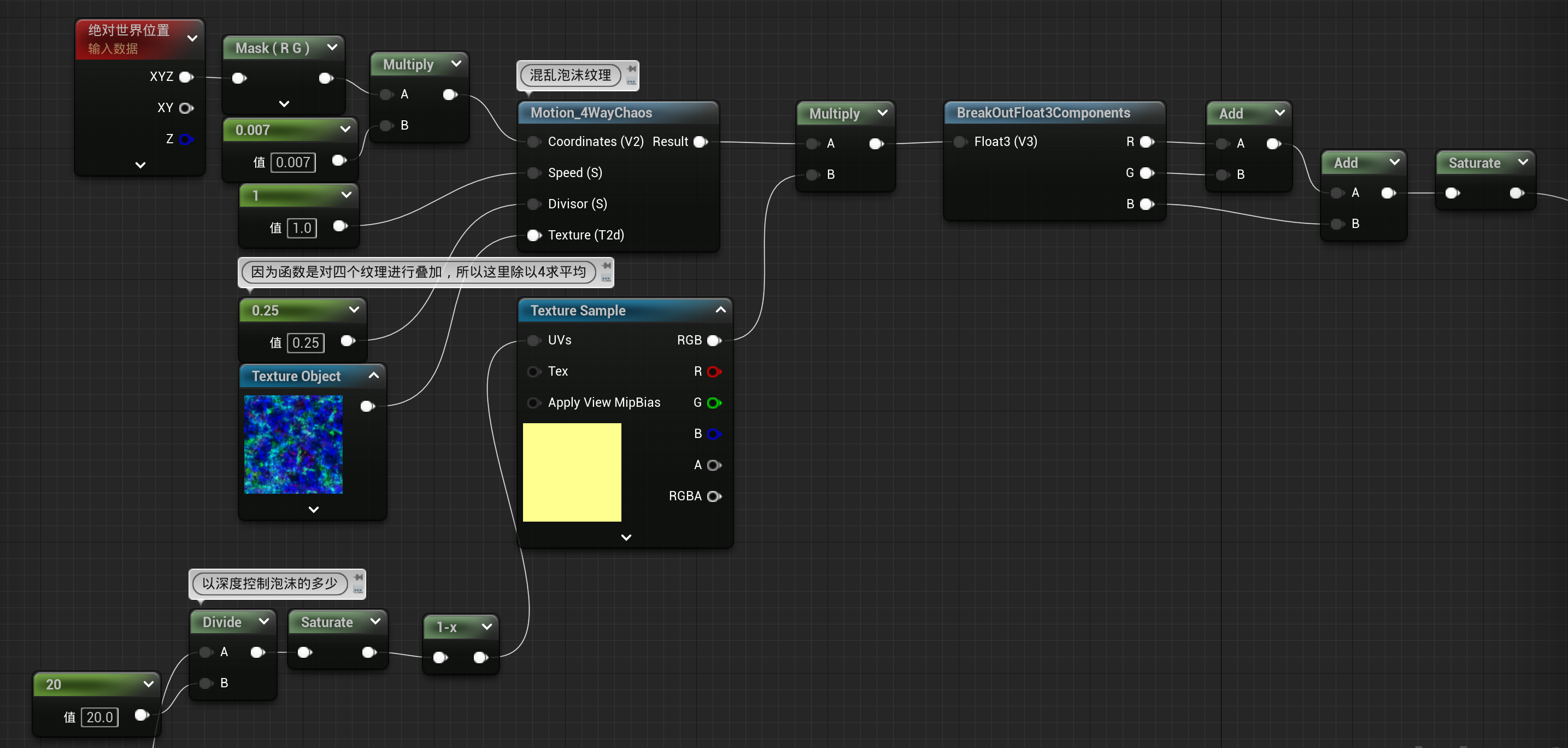
"divide"连下图的mask(B)
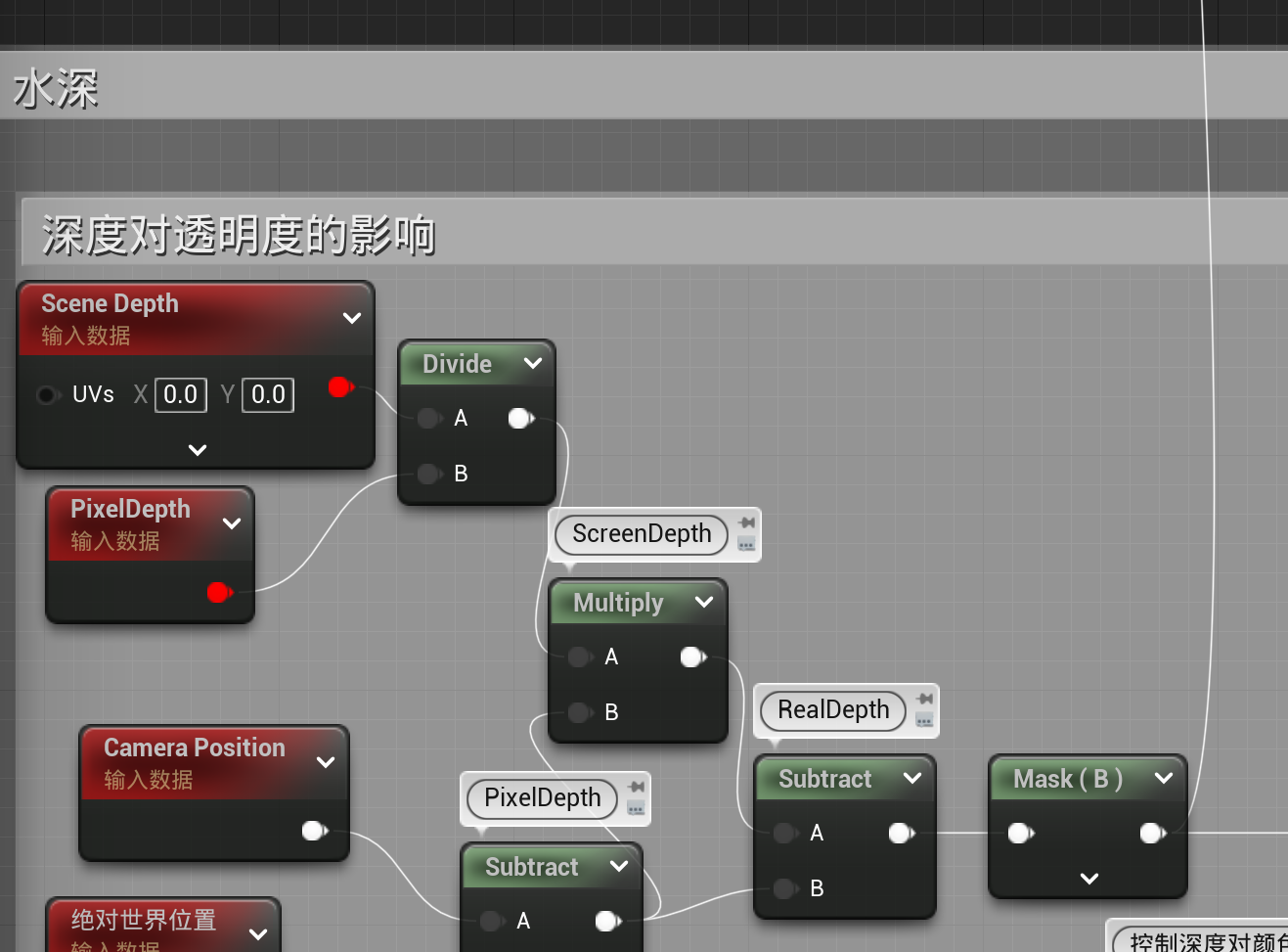

上色和不透明度
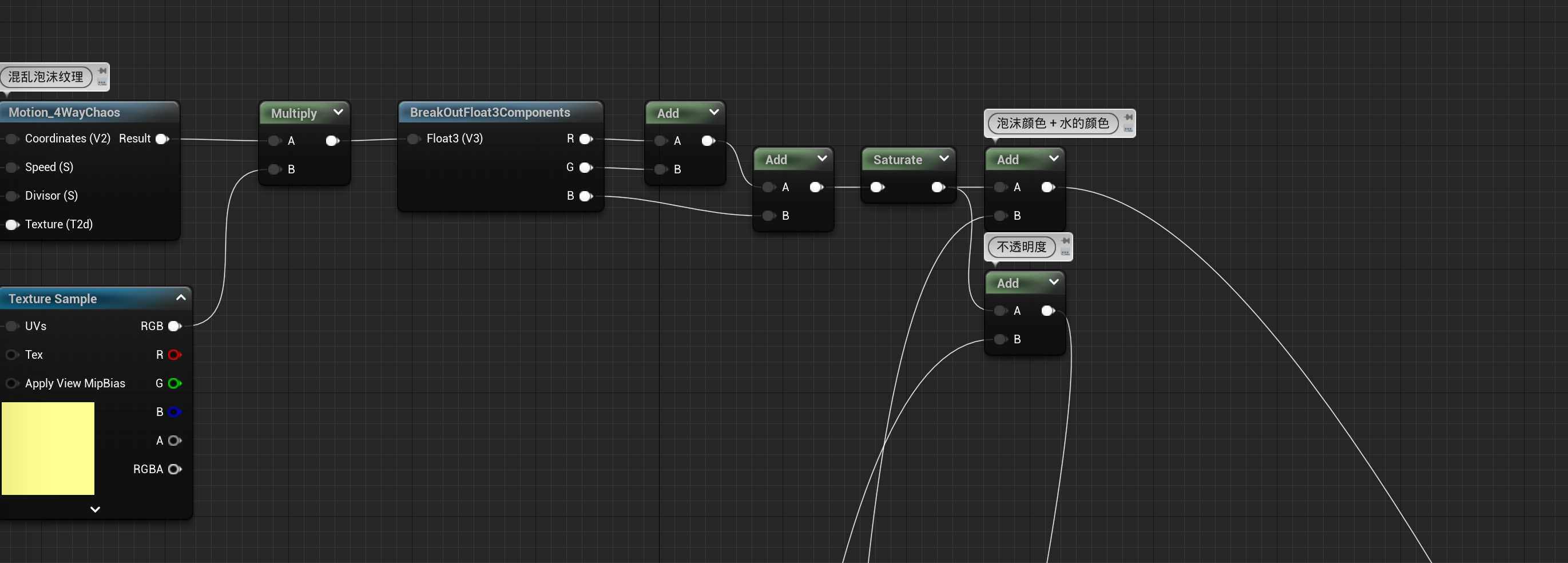
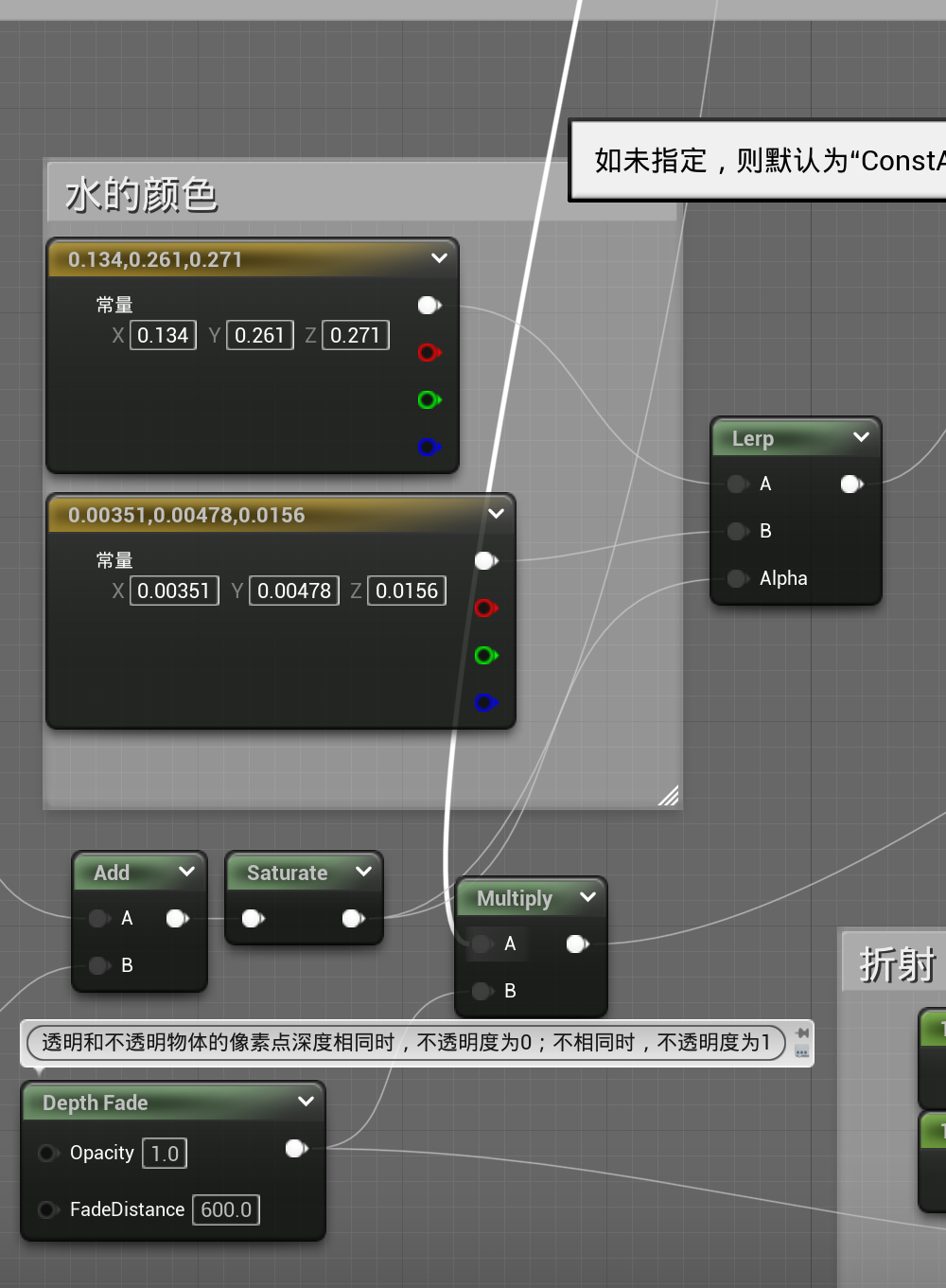
最终效果

水流
目标
实现类似溪流的水流效果,其有特定的流向
Flowmap的绘制及使用
Flowmap即水流贴图,其中每个像素表示水流的方向。但如何绘制该贴图呢?
有一款叫做FLOWMAP PAINTER软件专门用于绘制水流贴图
通过移动鼠标(下图中的圈圈)来绘制水流轨迹,绘制完毕后点击“Back to Texture”即可

随后导入UE中,再将其转换为法线贴图
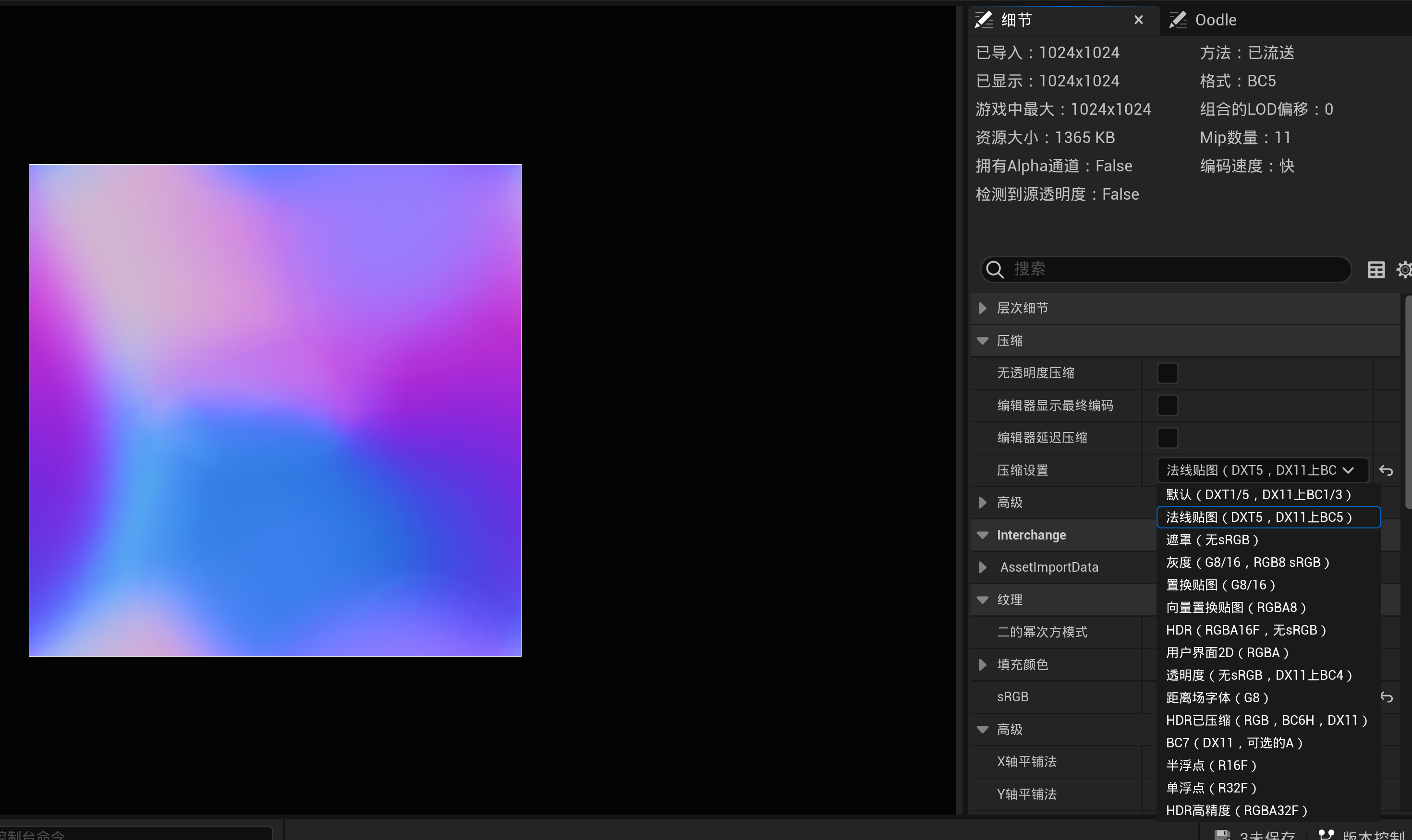
实现
初步实现
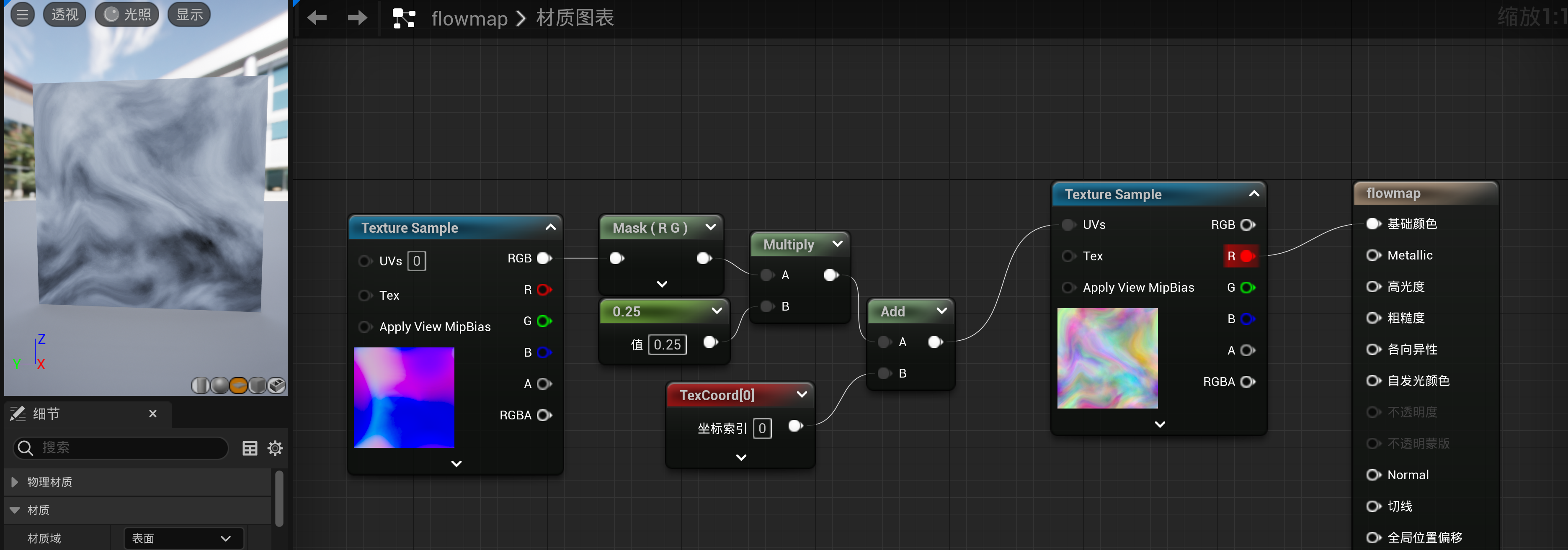
加入动画
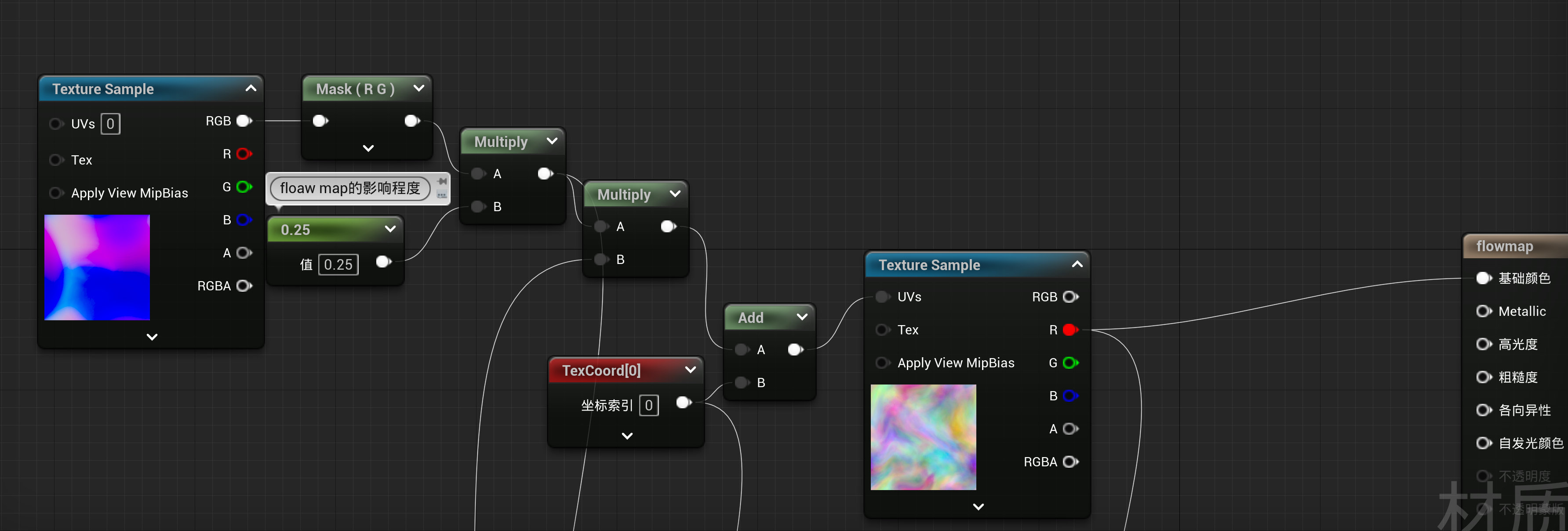

优化动画
从上图可以看到动画有终止,这并不是我们想要的水流效果
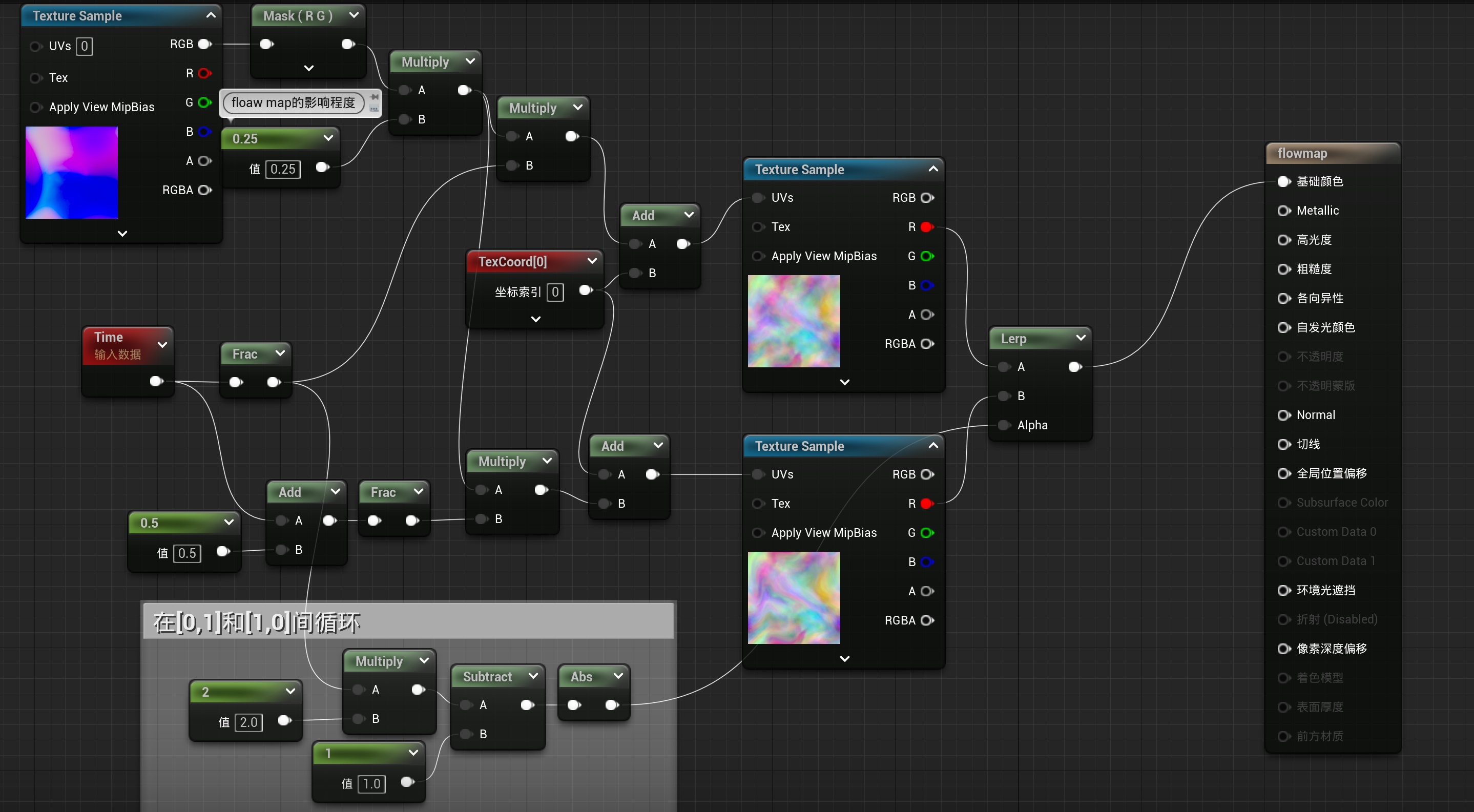

最终效果
封装为材质函数
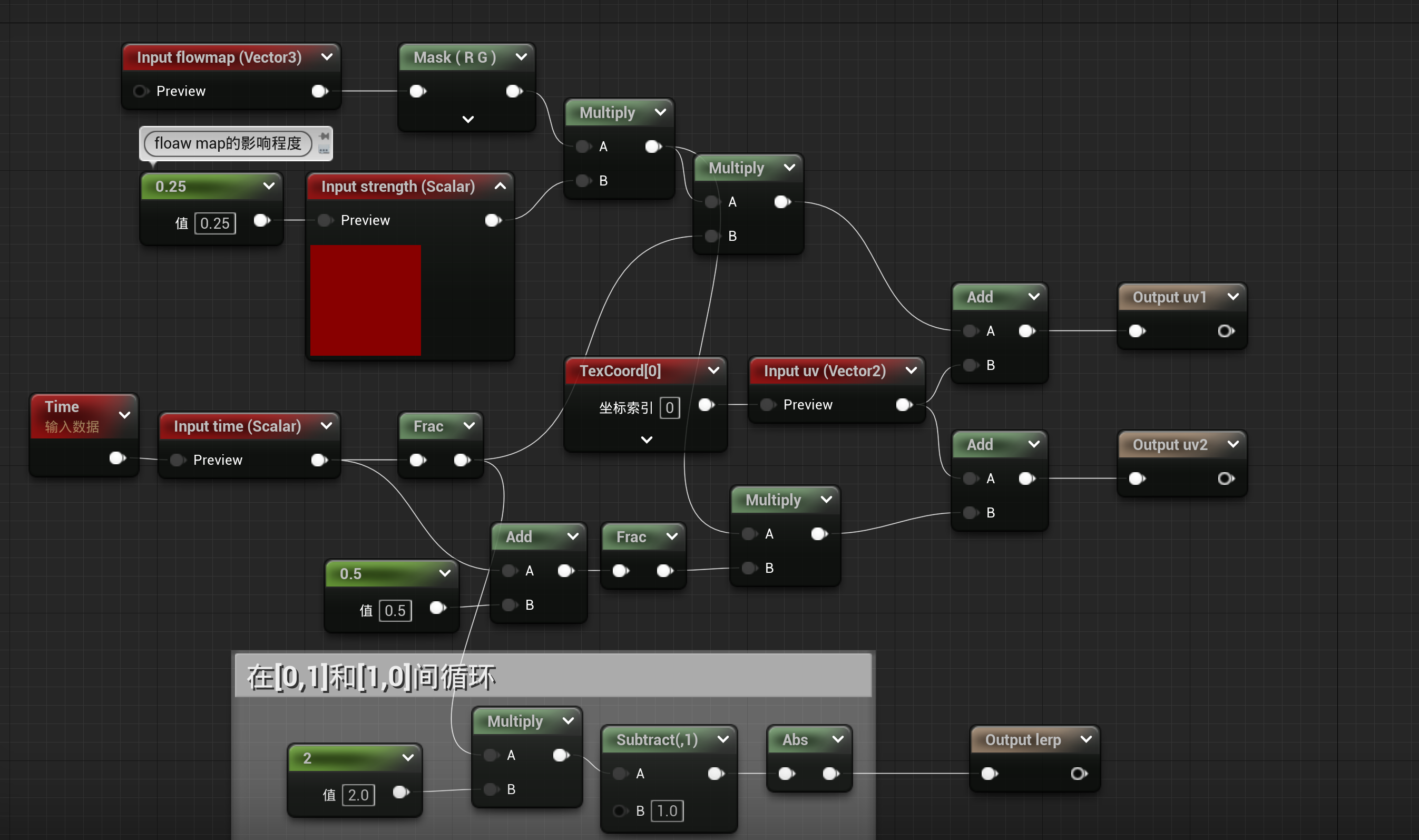
最后连接至根节点的normal
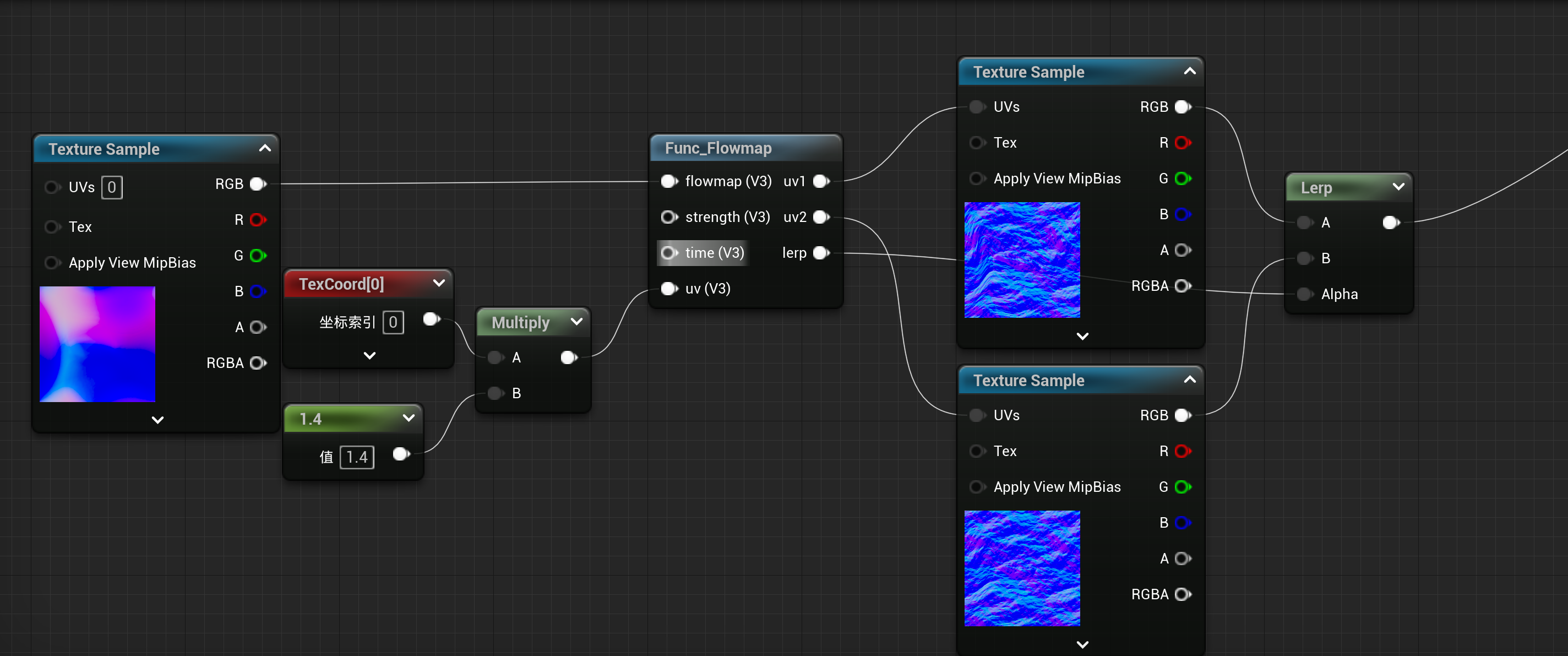

水下材质
加入后处理actor
依次点击“”放置Actor” 、”后期处理体积“”

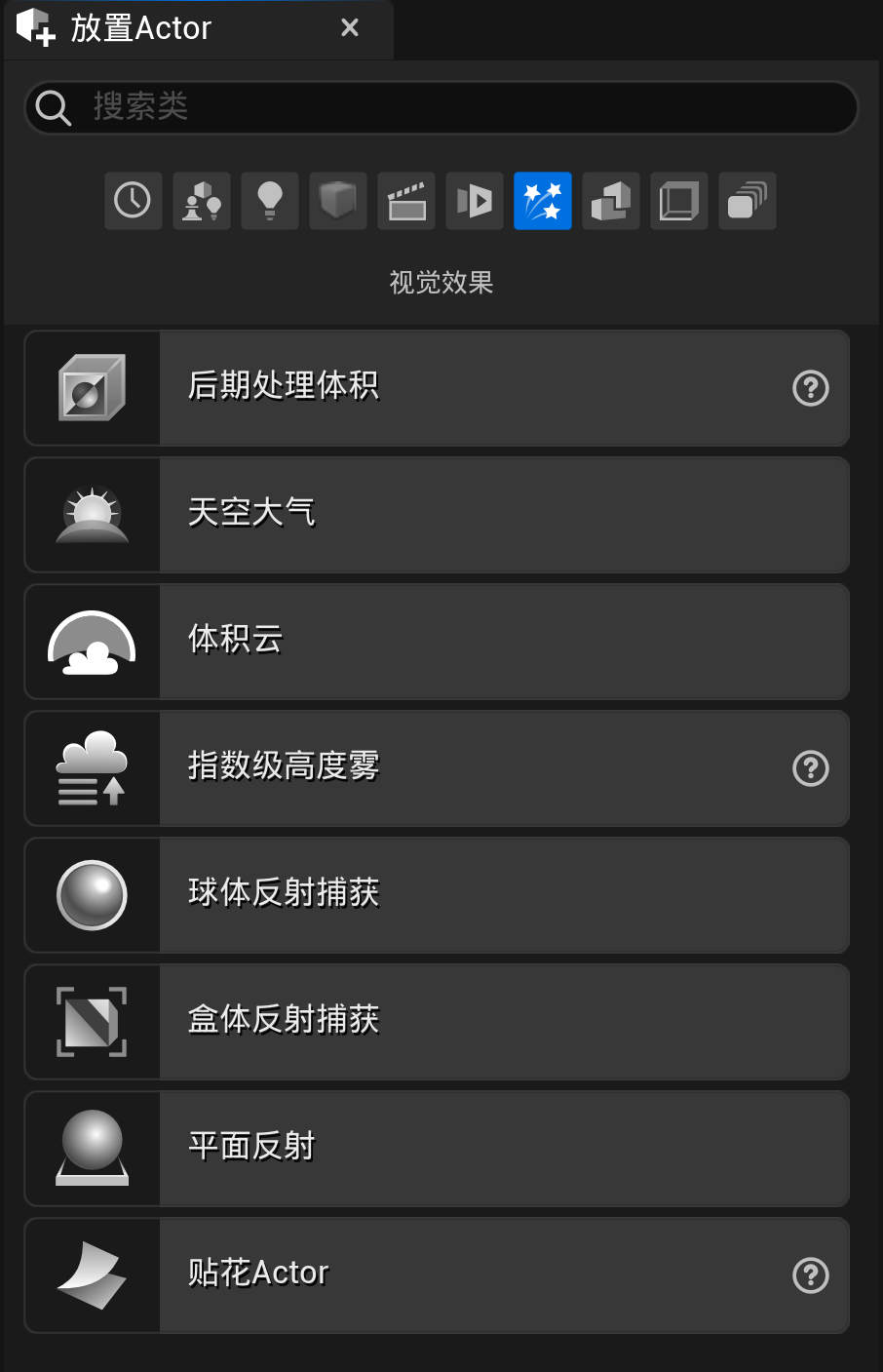
随后将该actor覆盖的面积调整为整个水下的面积
最后新建一个材质,并为后处理actor添加一个材质

赋予颜色
在开始前,需要将材质域改为“后期处理”
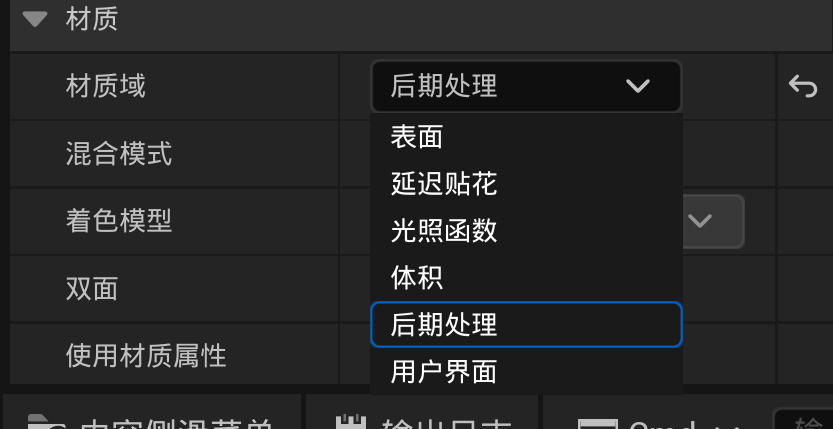
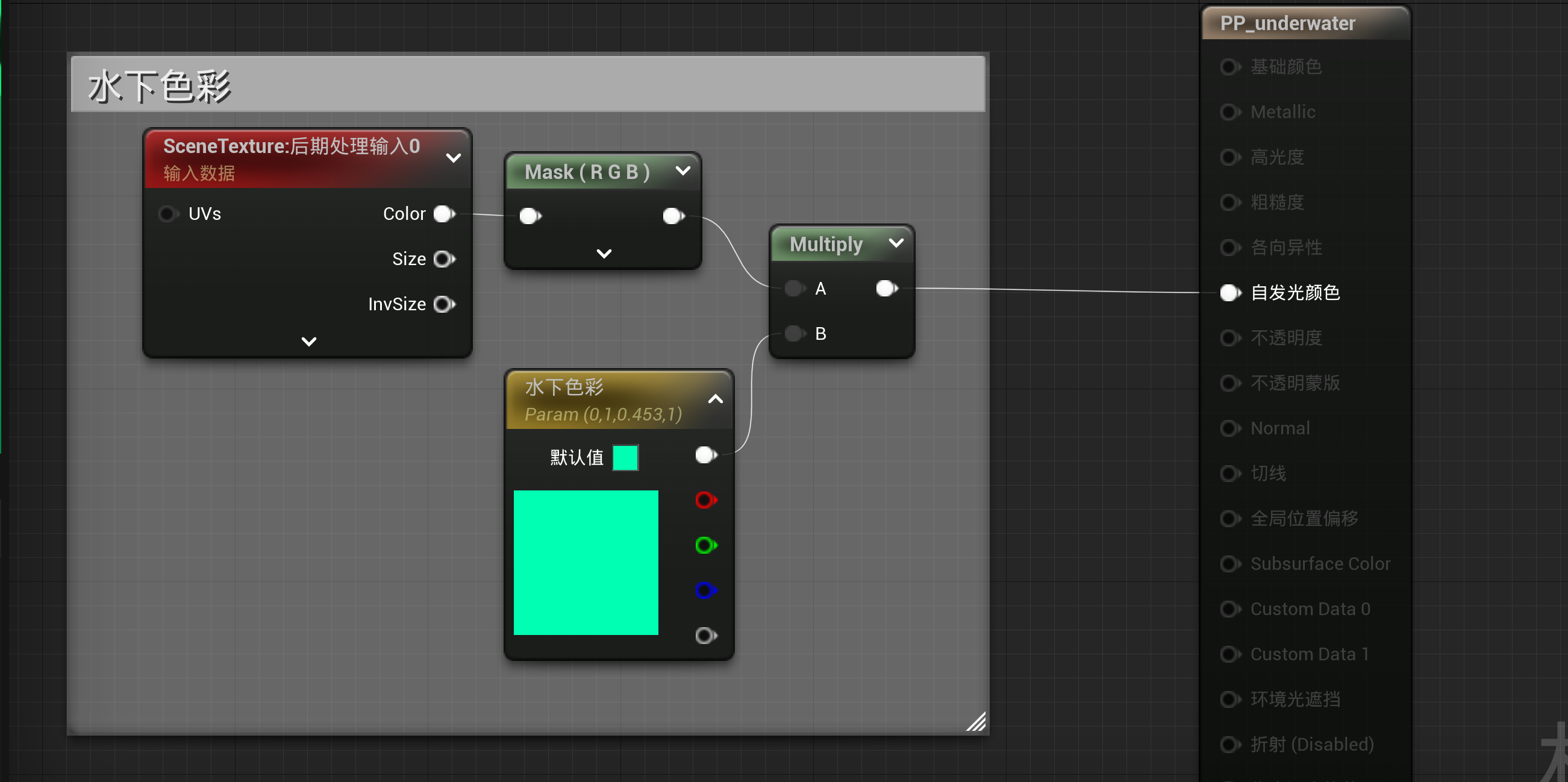
效果如下

雾效
但实际上上图的效果并不完全是理想的效果,实际上在水下的效果应是越近越清晰,越远越模糊,且视野中间清晰,越向左右两边靠近越模糊,也就是这里需要实现的雾效
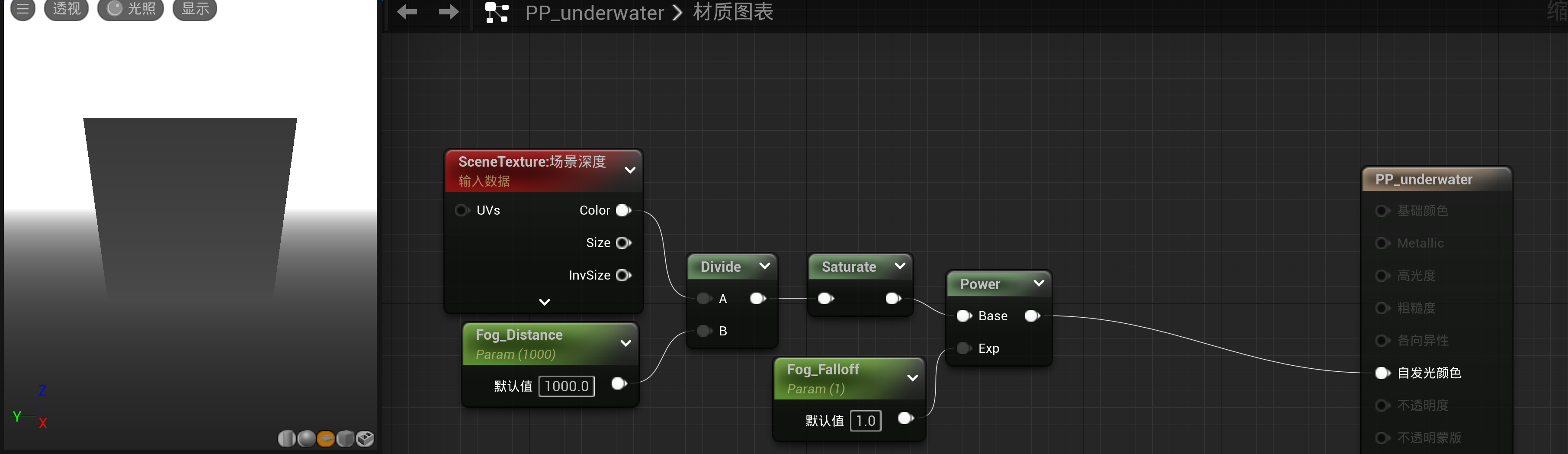

-
远近雾效
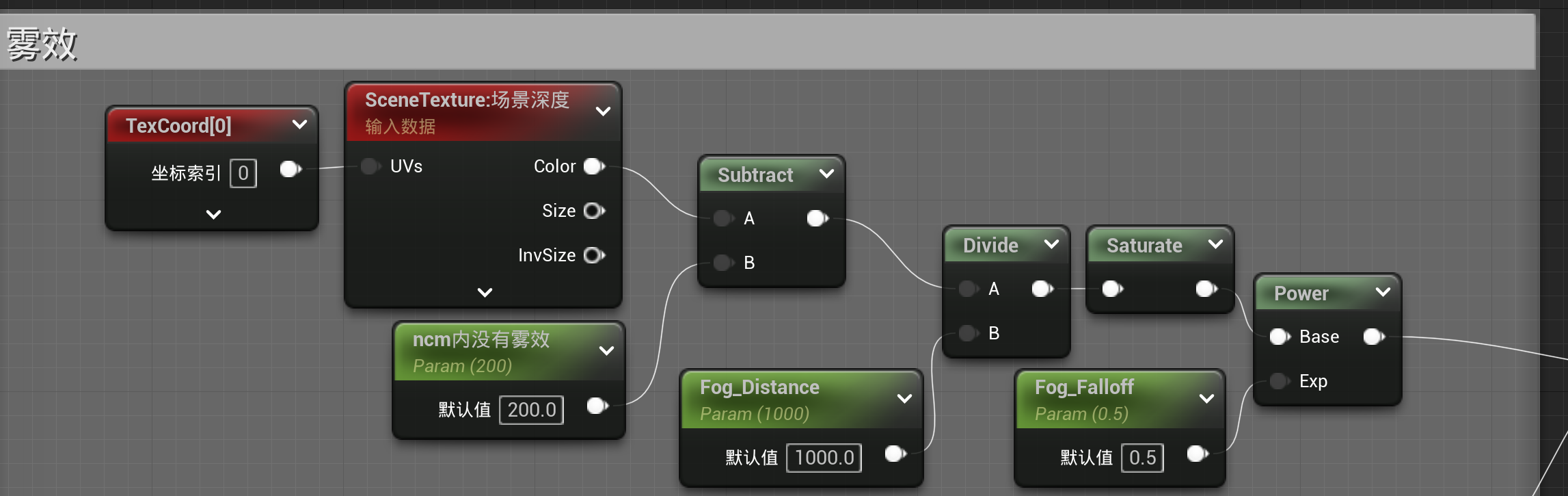

-
左右雾效
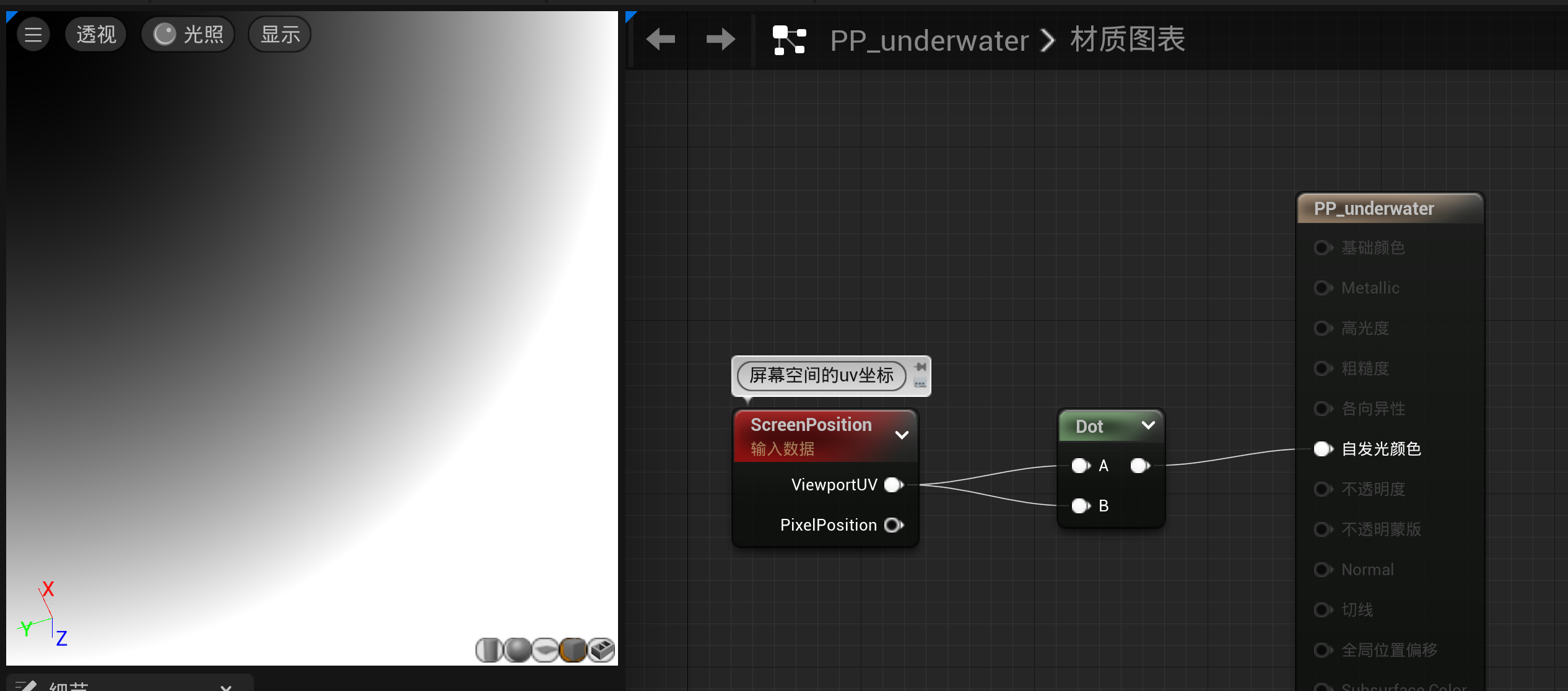
该方法实现出了一个中心黑两边亮的圆球,但我们想要的中心亮两边黑且该球需要处于屏幕中间
具体改动如下
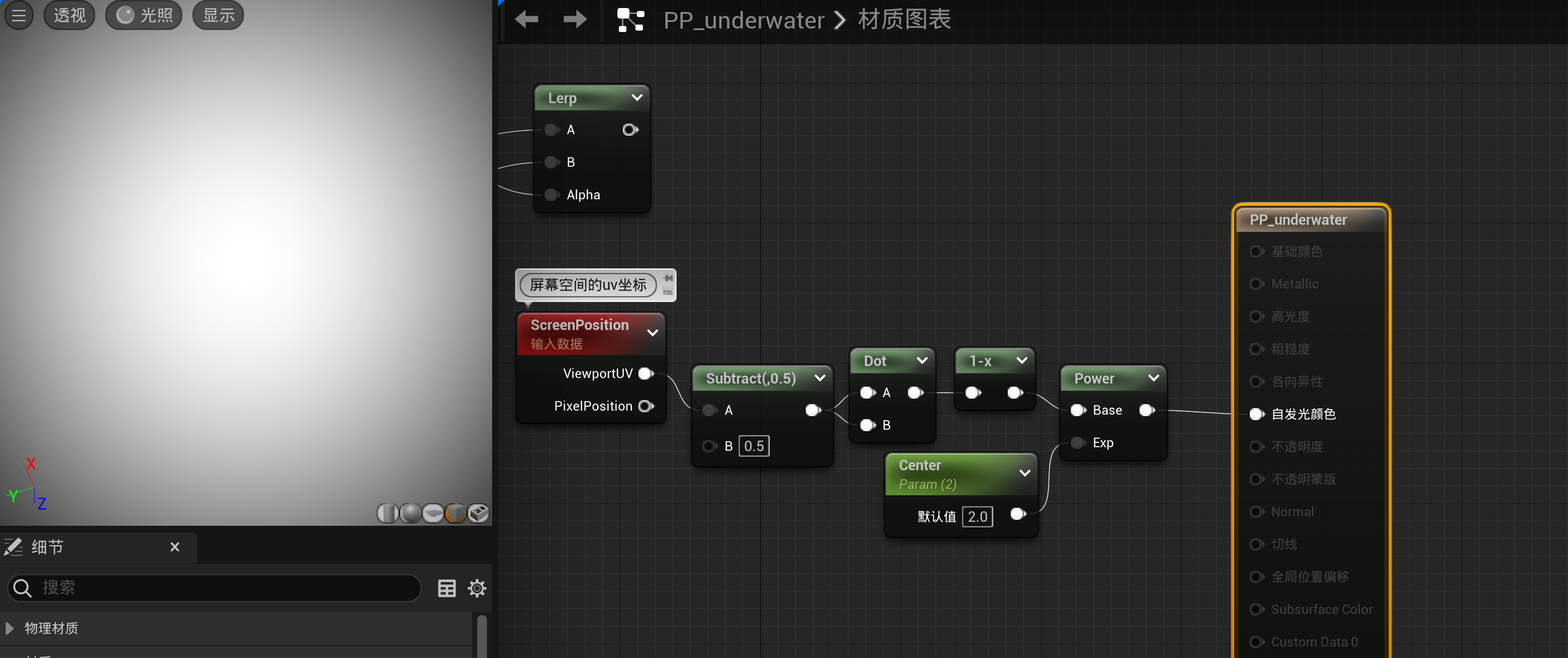
-
效果

模糊和锐化效果
-
思路
简单来说,实现模糊是加权平均的过程,依次选取屏幕上的像素点,对于每一个像素点都选取它周围的五个点,并进行加权求和
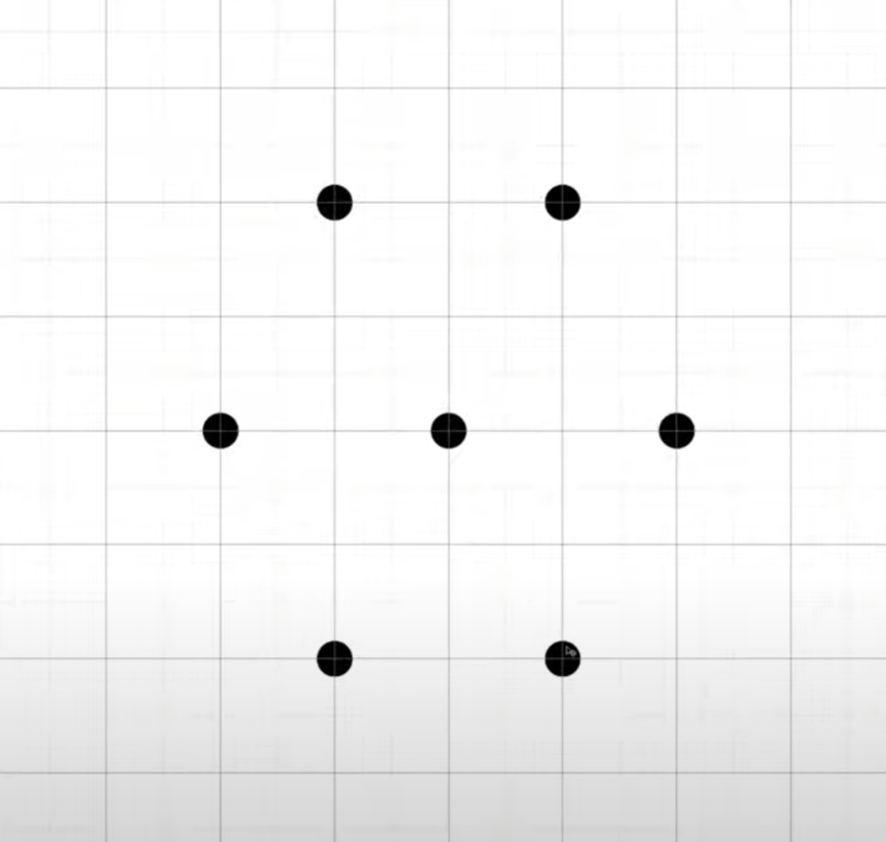
-
模糊实现
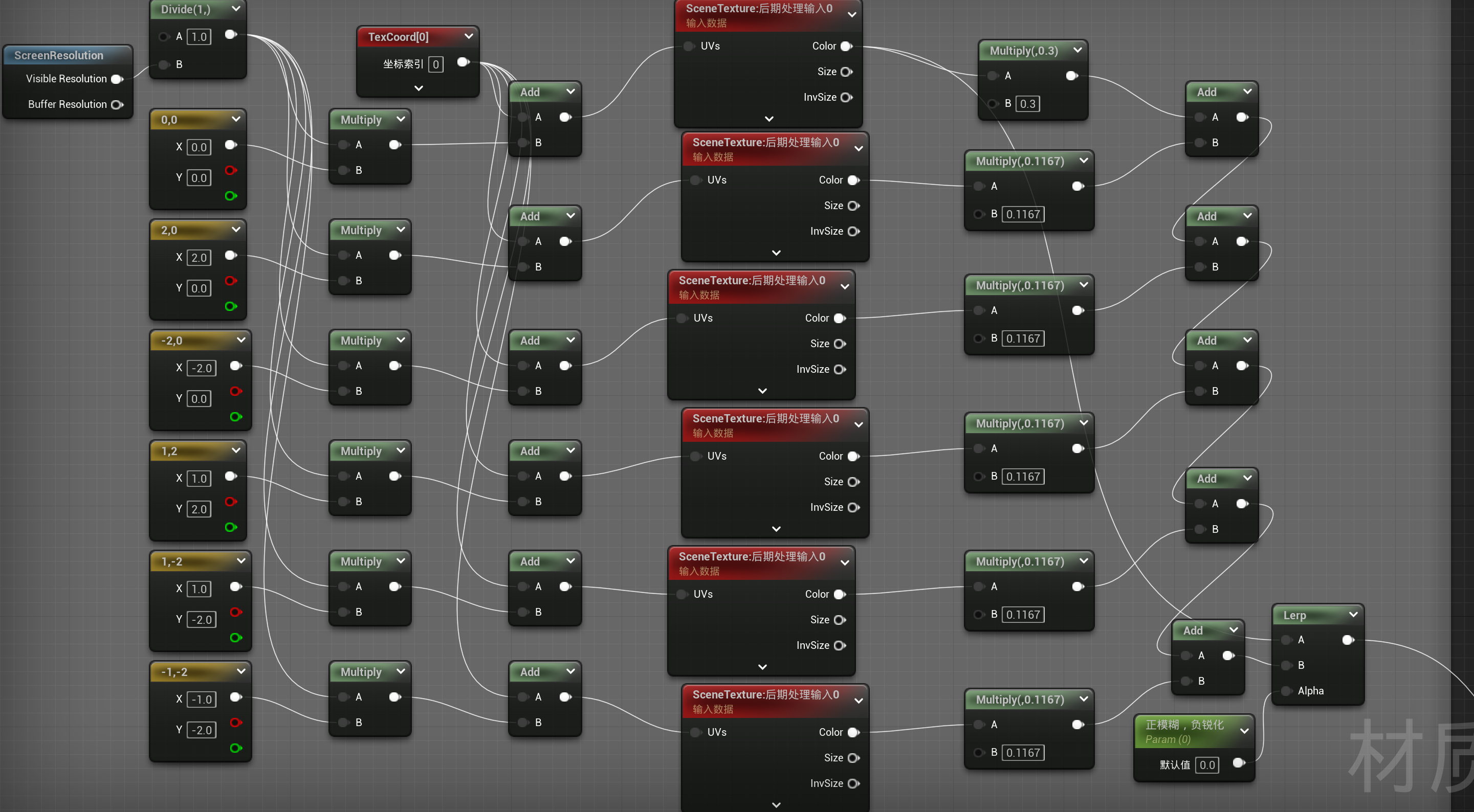

-
锐化实现
对上图中的lerp的alpha值取负即可实现锐化

放大图像
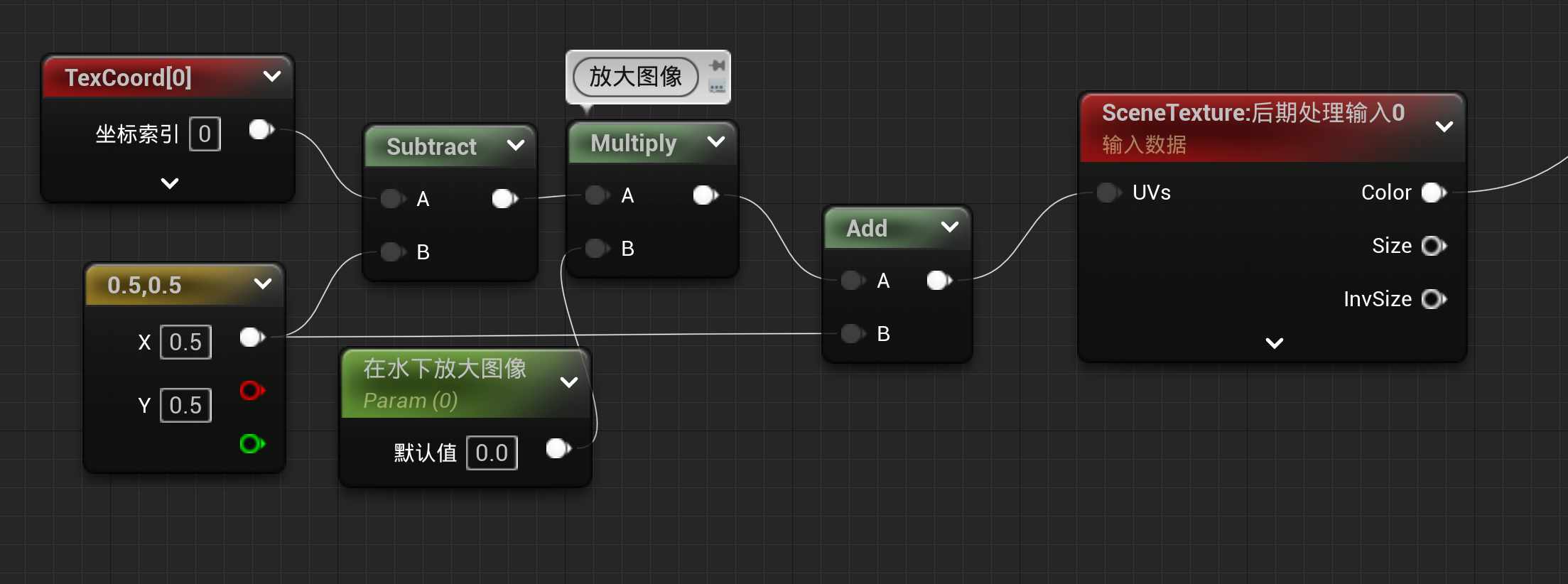

但我实际想要的是中间稍微放大,而边缘不怎么变化,这就需要用到mask
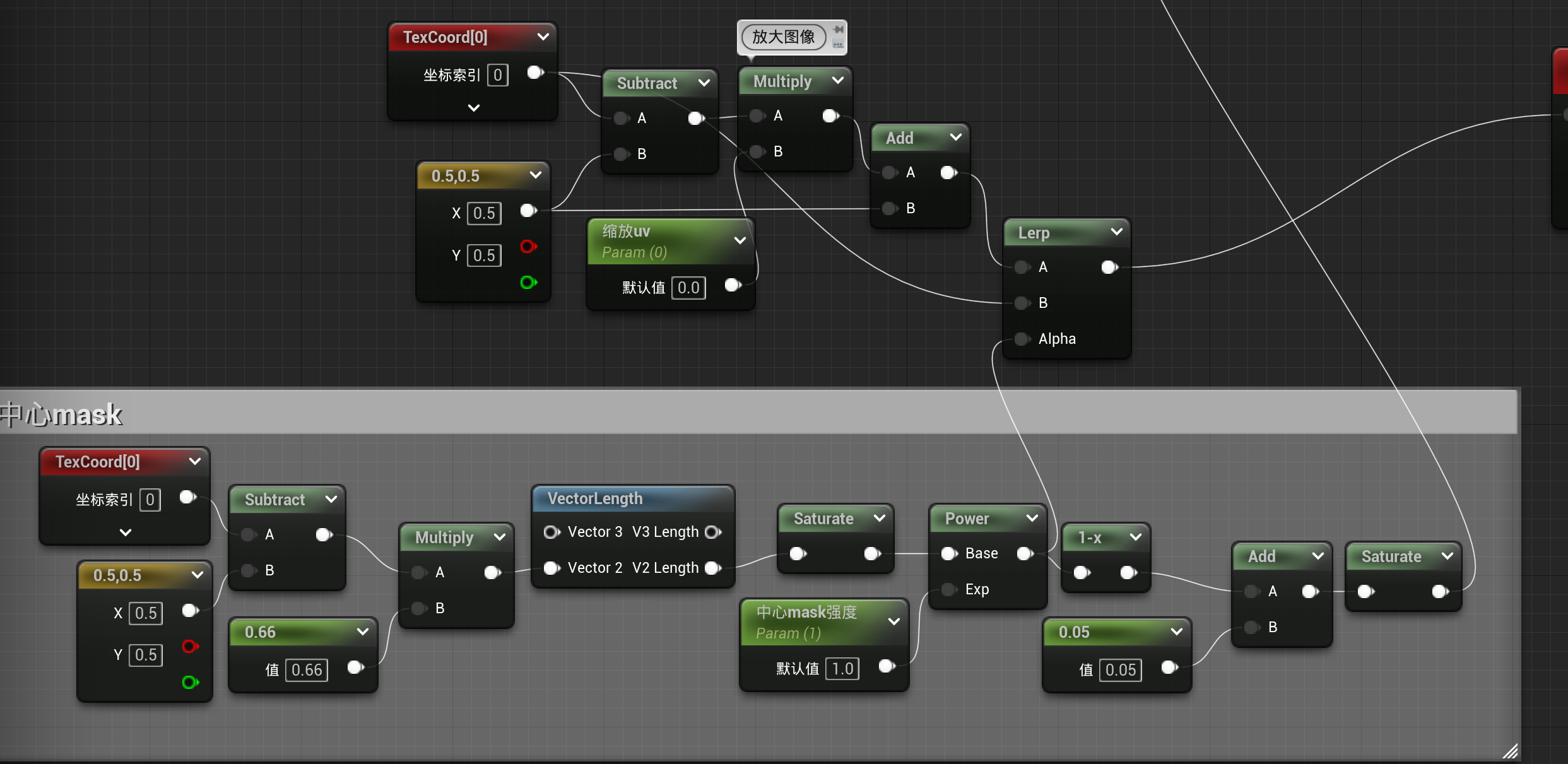
扭曲效果
这个效果在之前总结过,这里不再提及推导过程
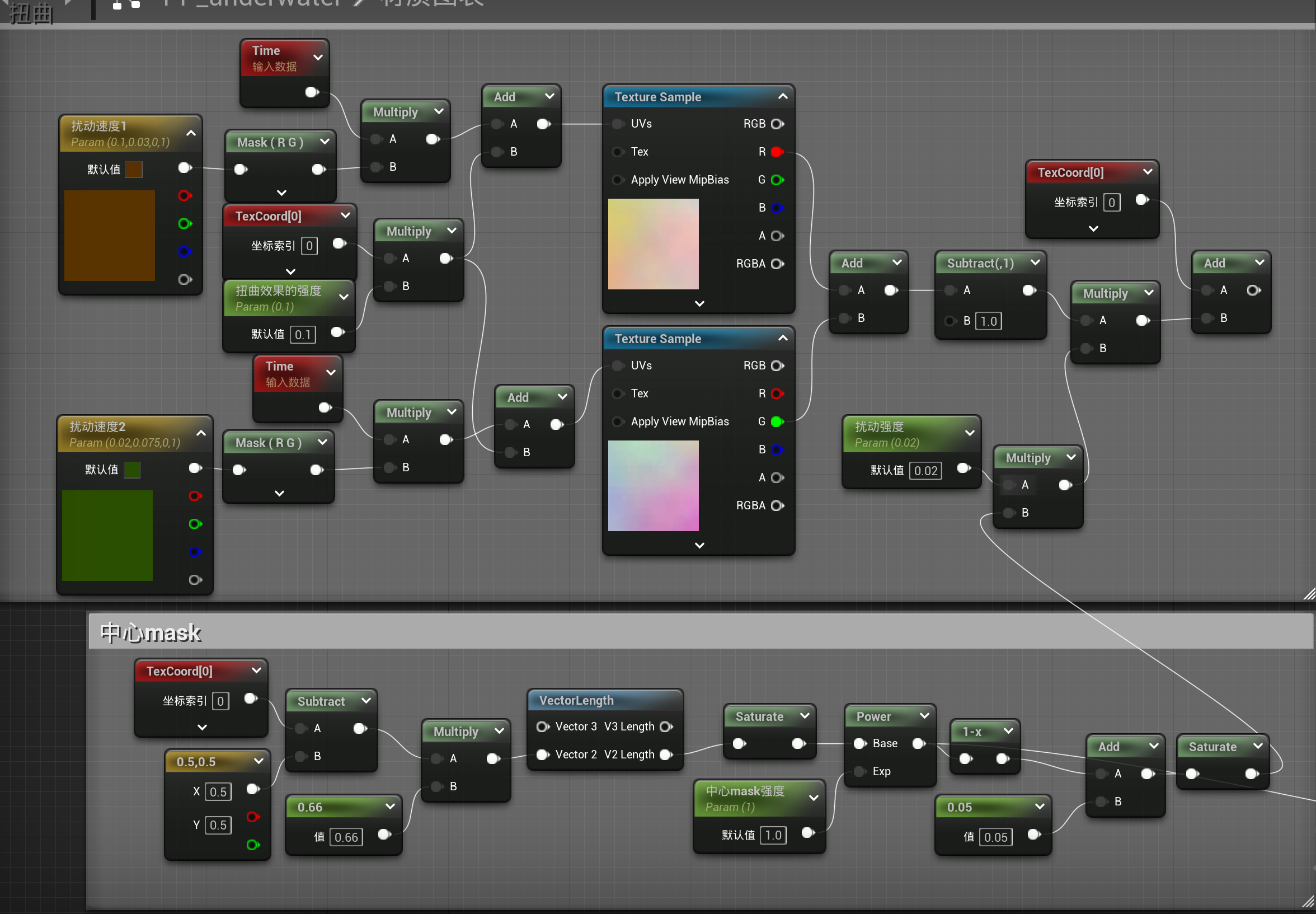
整合
接下来就是将上面的实现结合起来
首先求出扭曲效果的uv坐标后将其与放大效果结合
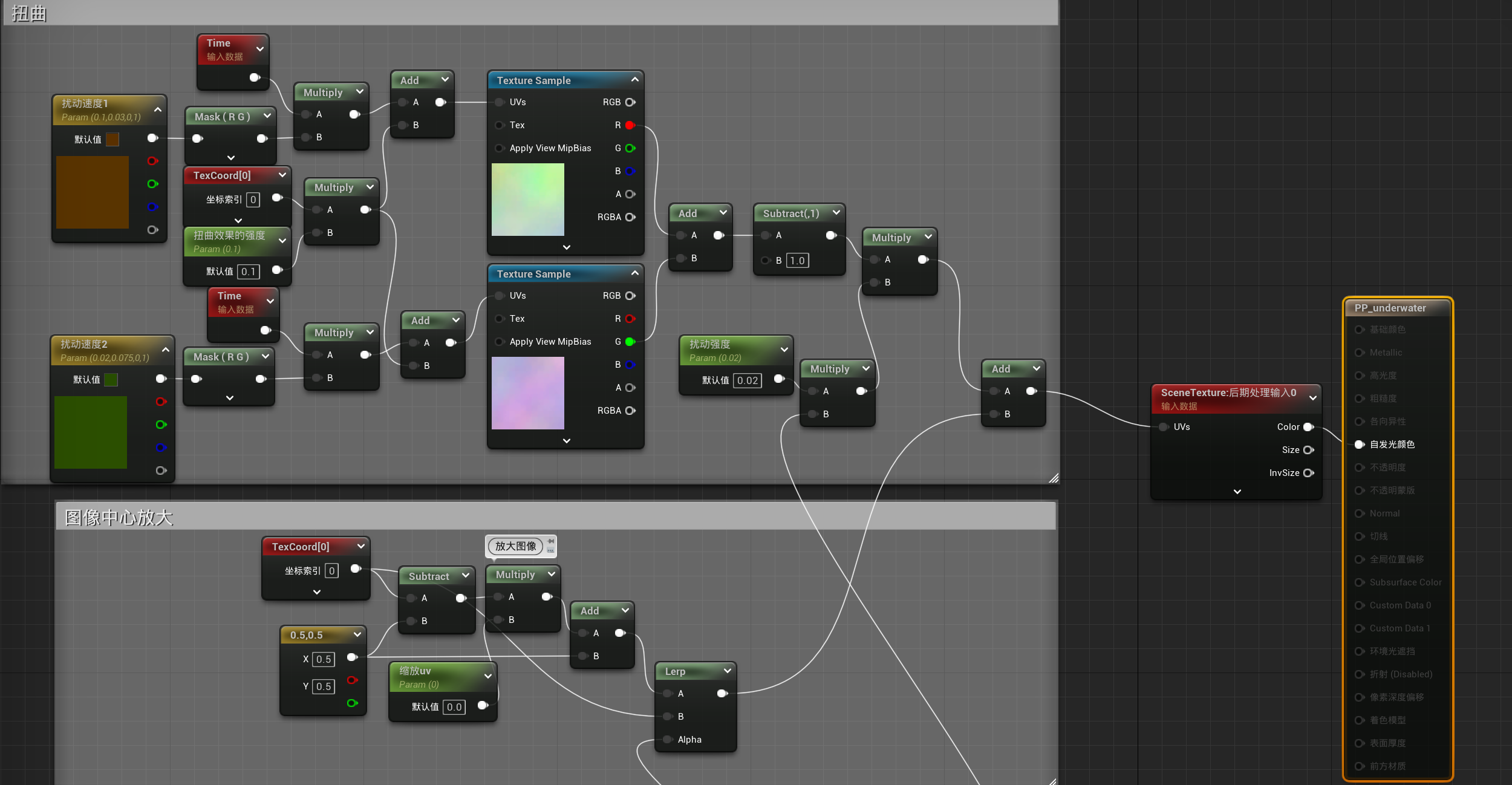

随后将新的uv与模糊效果结合
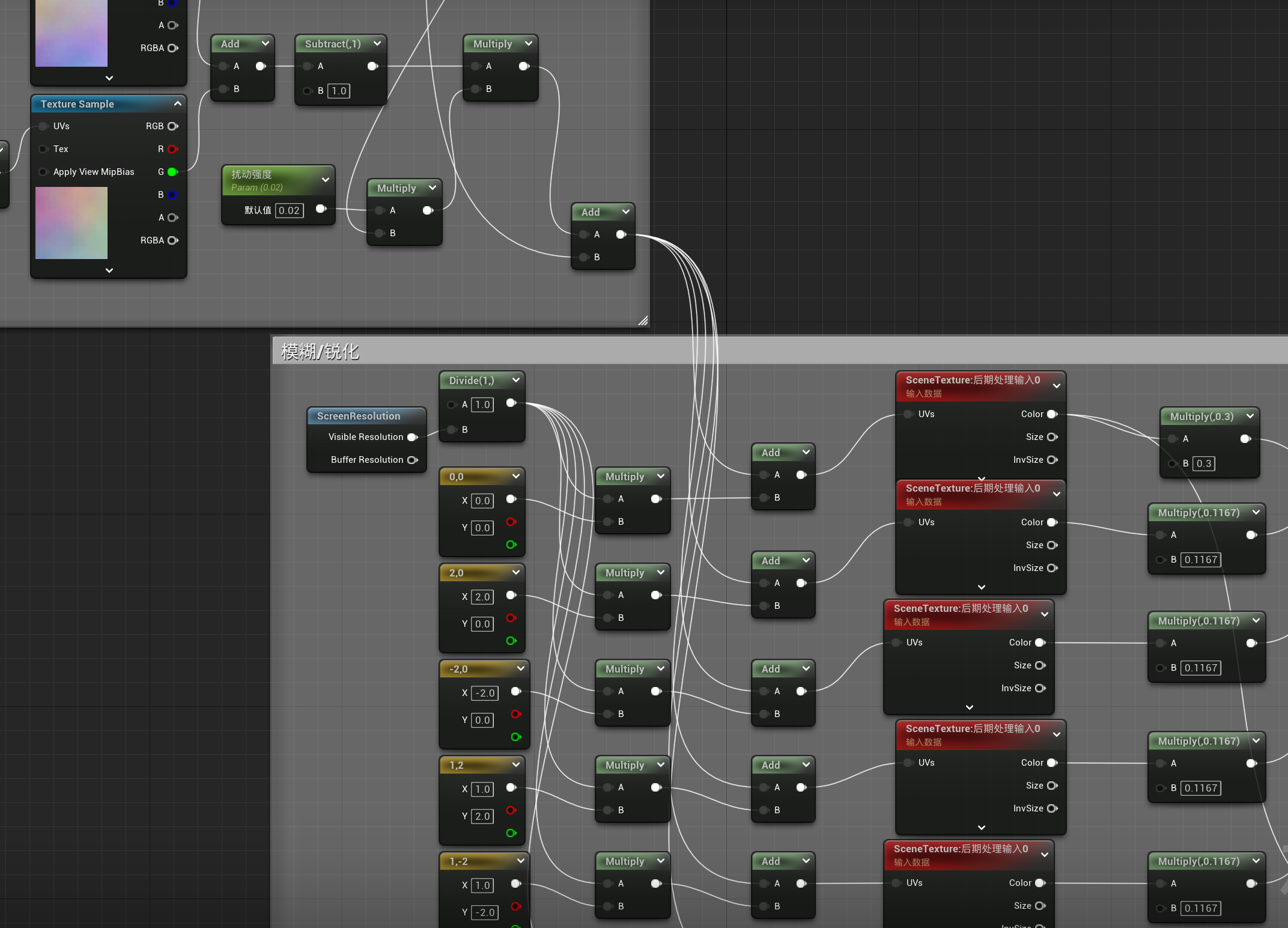
但需要注意的模糊效果应是从中间到边缘效果逐渐递增,因此需要用到mask
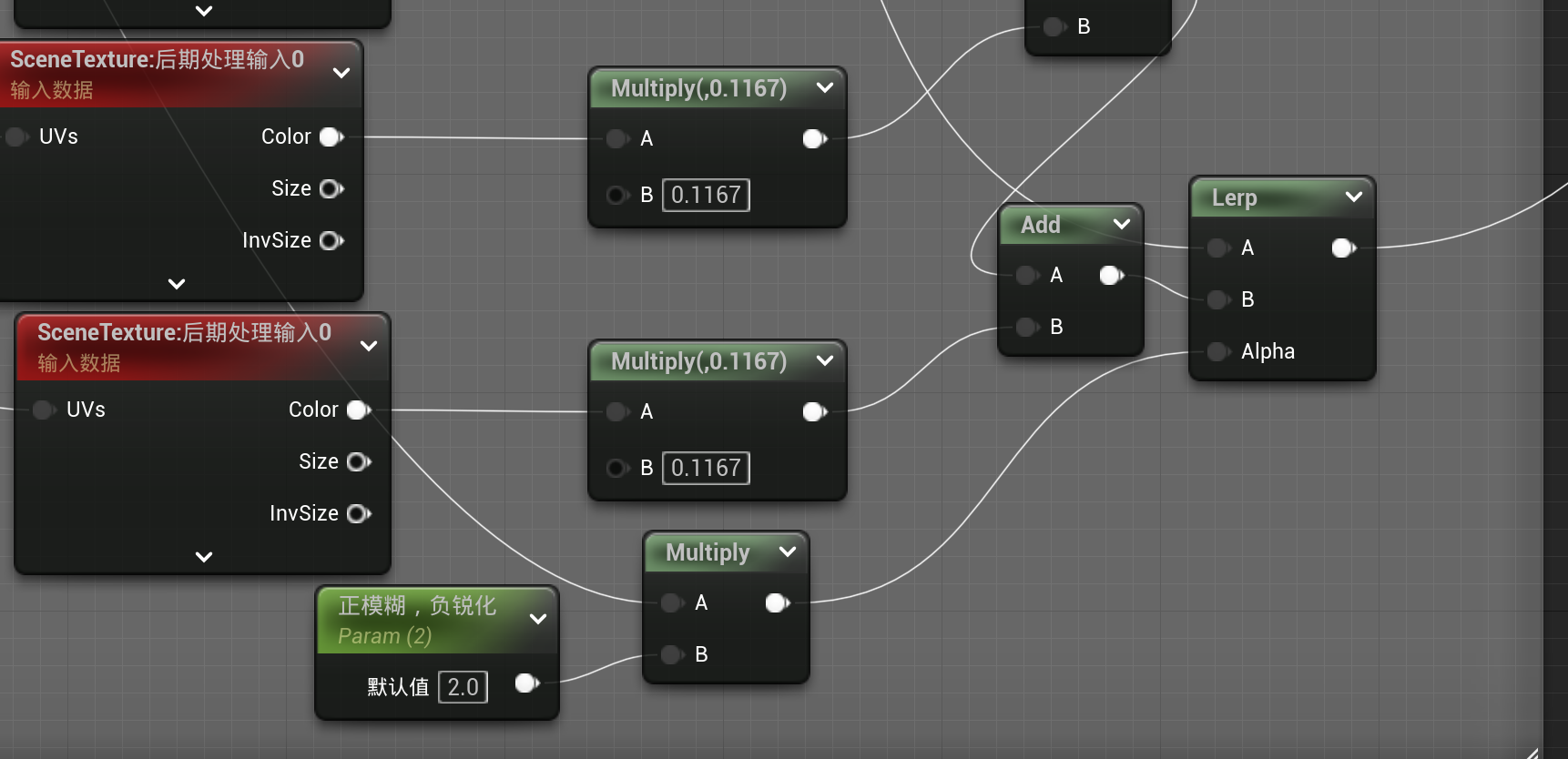
最后将得到的模糊后的颜色与水下颜色结合
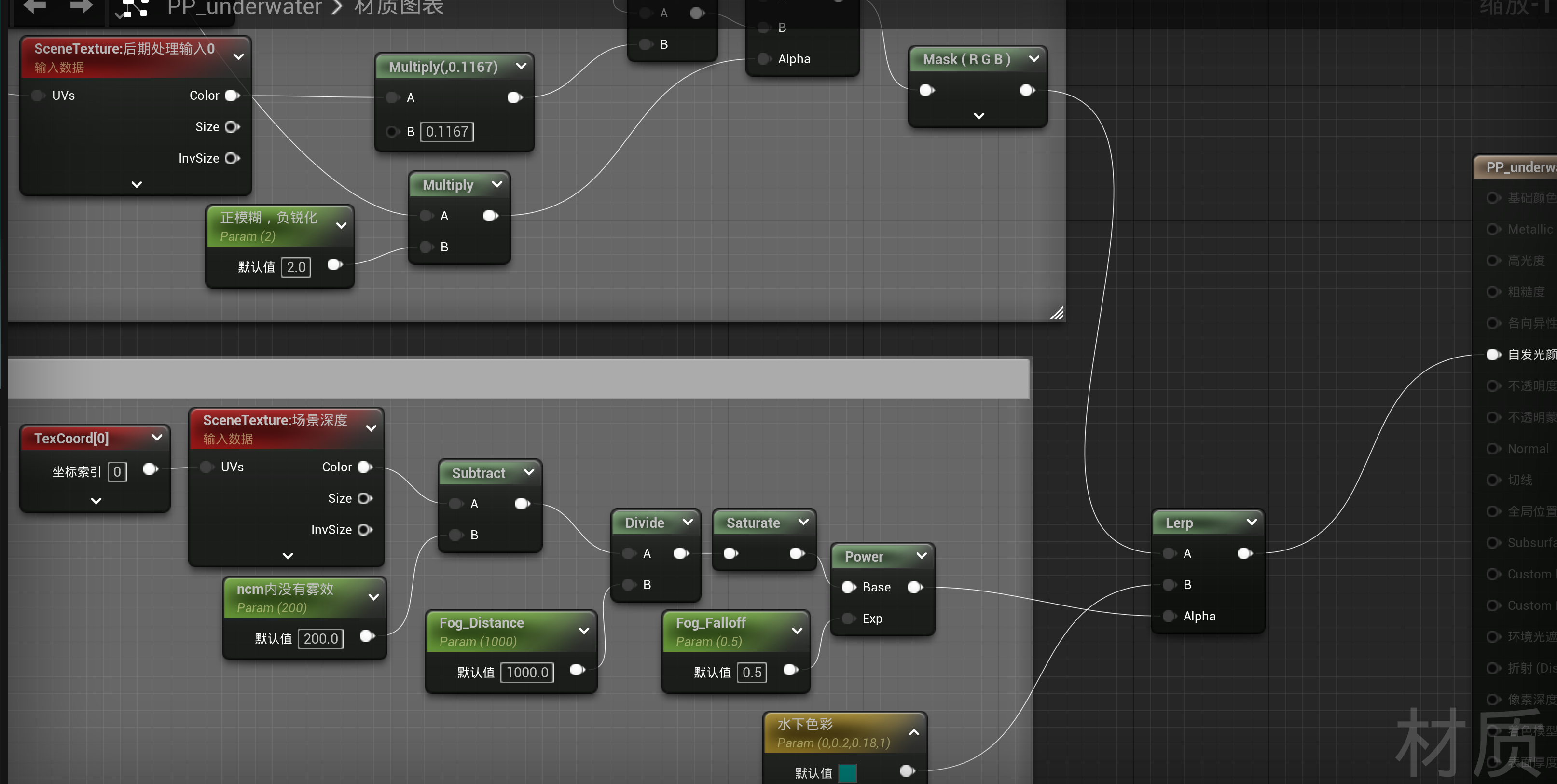
最终效果

reference
基于 Probe 的实时全局光照方案(Probe-based Global Illumination) - KillerAery - 博客园 (cnblogs.com)
[Siggraph15]Stochastic Screen-Space Reflections - 知乎 (zhihu.com)
虚幻引擎中的屏幕空间反射 | 虚幻引擎5.0文档 (unrealengine.com)
使用像素法线偏移实现折射 | 虚幻引擎文档 (unrealengine.com)
使用像素法线偏移实现折射 | 虚幻引擎文档 (unrealengine.com)
在虚幻引擎中使用像素法线偏移实现折射 | 虚幻引擎5.1文档 (unrealengine.com)
使用折射 | 虚幻引擎文档 (unrealengine.com)
GPU Gems1
[Game-Programmer-Study-Notes/README.md at master · QianMo/Game-Programmer-Study-Notes · GitHub](https://github.com/QianMo/Game-Programmer-Study-Notes/blob/master/Content/《GPU Gems 1》全书提炼总结/README.md#一、-用物理模型进行高效的水模拟(effective-water-simulation-from-physical-models))
水体渲染之Gerstner波形理解与推导 - 知乎 (zhihu.com)

