知识图谱顶会论文(ACL-2022) PKGC：预训练模型是否有利于KGC？可靠的评估和合理的方法

PKGC：预训练模型是否有利于KGC？可靠的评估和合理的方法

论文地址：Do Pre-trained Models Benefit Knowledge Graph Completion? A Reliable Evaluation and a Reasonable Approach

目录

• PKGC：预训练模型是否有利于KGC？可靠的评估和合理的方法
  • 摘要
  • 1.引言
  • 2.相关工作
    • 2.1 评估KGC
    • 2.2 KGC模型
      • 2.2.1 基于嵌入的KGC模型
      • 2.2.2 基于PLM的KGC模型
      • 2.2.3 基于提示的知识探测模型
  • 3.预备知识
    • 3.1 知识图谱补全(KGC)
    • 3.2 封闭世界假设(CWA)
    • 3.3 开放世界假设(OWA)
  • 4.模型方法
    • 4.1 框架
    • 4.2 三元组提示
    • 4.3 支持提示
    • 4.4 训练

摘要

近年来，预训练语言模型(PLM)已被证明可以从大量文本中获取事实知识，这促进了基于PLM的知识图谱完成(KGC)模型的提出。但是，这些模型在性能方面仍然落后于SOTA KGC模型。在这项工作中，我们发现性能不佳的两个主要原因：

1. 评估设置不准确。封闭世界假设(CWA)下的评估设置可能会低估基于PLM的KGC模型，因为它们引入了更多的外部知识。
2. PLM使用不当。大多数基于PLM的KGC模型只是简单地将实体和关系的标签拼接为输入，导致句子不连贯，无法充分利用PLM中的隐含知识,因此在性能方面仍然落后于SOTA KGC模型。

SOTA：state-of-the-art,即最前沿的，最先进的，目前最高水平的。

为了缓解这些问题，我们强调了开放世界假设(OWA)下更准确的评估设置，它手动检查KG中不存在的知识的正确性。

此外，在及时调整的思想的启发下，我们提出了一种新的基于PLM的KGC模型，名为PKGC。基本思想是将每个三元组及其支持信息转换为自然提示句，进一步输入PLM进行分类。

在两个KGC数据集上的实验结果表明OWA在评估KGC时更可靠，尤其是在链路预测方面，以及我们的PKCG模型在开放世界和OWA设置上的有效性。

1.引言

知识图谱(KG)已逐渐成为许多NLP任务的基石，是表示世界知识最有效的方法之一。为了提高知识的覆盖率，研究人员采用了自动化的知识提取技术或依靠协同编辑，但这些知识库仍然难以覆盖现实世界中大量的新兴知识。这个问题促进了KGC的研究，即通过理解KG中的现有结构来预测缺失链接。

用于KGC的预训练语言模型(PLMs)的潜力很快席卷了整个NLP领域，引起了广泛关注。PLMs从大量未标记的文本中隐含地获取了事实知识，这可能有助于补充缺失的知识。KG-BERT首次将PLM引入KGC，它将三元组中实体和关系的标签拼接起来作为PLMs的输入，以验证其正确性。在KG-BERT的基础上进一步引入了多任务学习。然而，上述基于PLMs的KGC模型的结果并不乐观，甚至与传统的知识图嵌入(KGE)模型相差甚远。这就提出了一个问题:为什么PLM中学到的事实知识对KGC没有太大帮助?

在本研究中，我们发现了基于PLM的KGC模型性能较弱的两个主要原因:

1. 不准确的评估设置。大多数现有的KGC模型都是在封闭世界假设(CWA)下进行评估的，该假设在给定的KGs中未知的任何知识都是不正确的。这样的设置有利于自动构建数据集，而无需手动注释。然而，PLMs的引入带来的很多未知的外部知识，都是在CWA下被认为是不正确的，这错误地降低了模型的性能。如图1所示，对于一个三元组查询(England,contain,?)，基于PLM的KGC模型给出了许多正确的尾部实体(用粗体突出显示)，但只有Pontefract在CWA下被认为是正确的，因为它存在于KGs中。
   

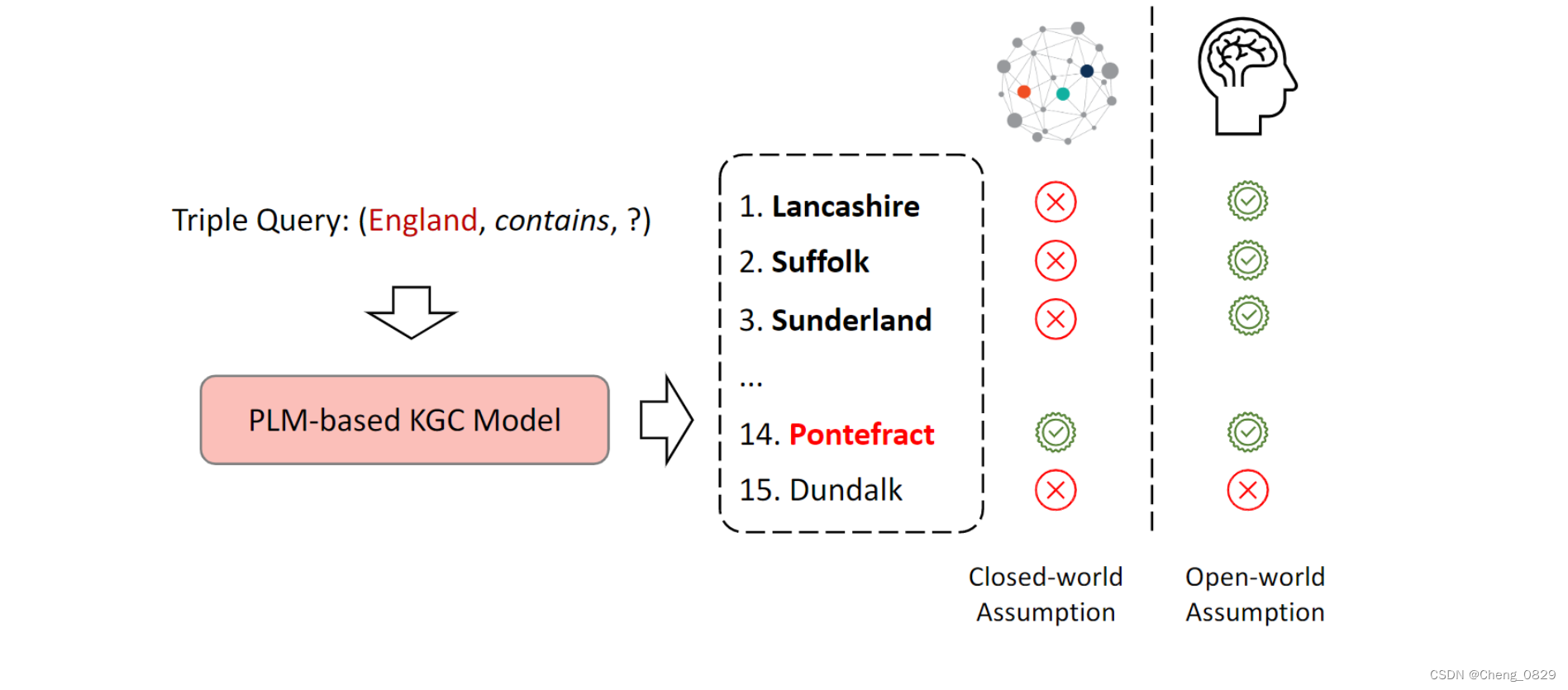
   图1: 不同设置下链路预测的评价结果。虚线框中粗体的实体都是正确答案，在封闭世界假设下，只有红色实体被认为是正确的；在开放世界假设下，虚线框中粗体的实体均被认为是正确的。

2. 没有正确利用PLMs。现有的基于PLM的KGC模型只是将实体的标签和三元组中的关系拼接起来，作为PLM的输入。这导致句子不连贯，与预先训练的任务有区别，因此不能充分利用PLM中的知识。

为了缓解上述两个问题，我们提出了一个新的基准设置来纠正这一研究方向，并提出了一个新的基于PLM的模型。为了使KGC评估更加可信，我们强调了一个基于开放世界假设(OWA)的新的评估设置——不在KGs中的知识不是错误的，而是未知的。因此，CWA下的假正类应该被去除，只需要我们从未知中识别出准确的真和假三元组。对于这些未知的三元组，我们进行人工注释以检查它们是否有效。

我们进一步提出了一种新的基于PLM的KGC模型PKGC，以便更好地隐藏在PLM参数中的隐性知识。受基于提示的模型的激励，基本思想是将每个三元组转换成自然的提示句，而不是简单地拼接它们的标签。具体来说，我们为每个关系类型手动定义提示模板，并进一步引入软提示，以更好地表达三元组的语义。此外，得益于提示的调整，PKGC可以灵活地考虑三元组的上下文，例如定义和属性，将它们作为支持提示插入三元组提示的末尾。

提示学习(Prompt Learning)：类似于Fine-Tuning，但是对资源的需求更低

我们对来自Wikidata和Freebase的两个KGC数据集进行了实验，并在OWA而不是CWA中，对基于KGE和基于PLM的KGC模型进行了重新评估。根据实验结果，我们发现:

1. OWA对KGC提供了更准确的评估，特别是对更有知识的基于PLM的KGC模型和更开放的链接预测任务。
2. 我们的PKGC模型通过将三元组和辅助信息转换为自然提示句，可以有效地利用PLM在KGC任务中的知识，从而降低了对训练数据量的敏感度。
3. 模型性能良好的原因不仅在于PLMs在大量文本中看到了部分相关知识，还在于我们的模型具有推理能力，可以结合PLMs和KGs的知识推断未知知识。

2.相关工作

2.1 评估KGC

大多数现有的KGC模型在CWA下进行评估，因为可以自动构建数据集。然而，CWA本质上是一个近似的假设，可能会带来不准确的评价结果。

OWA很少被用于评估KGC模型的性能，因为它需要对未知的三元组进行手动注释。近年来，有两个数据集CoDEx和InferWiki为OWA下的三元组分类提供了评价数据集。此外，有人还评估了OWA下知识图嵌入的校准。尽管这些工作是在OWA下部分执行的，但他们只将OWA作为一个附加的实验设置。

在本研究中，我们率先系统性地比较了在CWA和OWA下不同模型和不同任务之间的差异，发现CWA不能准确反映KGC模型的真实性能，这在基于PLM的KGC模型和链路预测任务中表现得更为明显。

2.2 KGC模型

2.2.1 基于嵌入的KGC模型

KGE模型是KGC早期的主流方法。KGE模型可以分为三类:

1. 基于平移的模型
2. 基于张量因子分解的模型
3. 非线性模型。

此外，还有一些KGE模型可以进一步引入额外的信息，如文本和属性。

2.2.2 基于PLM的KGC模型

基于PLM的KGC模型对KGC任务上的PLM进行微调，以利用PLM中的隐性知识和KGs中的结构化知识。KG-BERT是第一个使用PLM执行KGC的模型。它只是将实体和关系的标签拼接成三元组来作为PLM的输入。有人在KG-BERT的基础上进一步引入了多任务学习，此外还有人关注零样本学习设置。与我们的模型相比，这些模型都只是简单地将标签拼接成三元组，导致句子不连贯，不能充分利用PLM中的隐性知识。

2.2.3 基于提示的知识探测模型

基于提示的知识探测模型旨在探测PLM包含了多少知识。因此，他们不会对KGC任务上的PLM进行微调。LAMA 是第一个基于提示的知识探测模型，它将一个三元组查询转换为带有掩码[MASK]的句子，并使用掩码[MASK]的输出作为预测实体。基于LAMA，有一些模型从自动模板生成和添加软提示进行改进。这些模型专注于探测，没有使用KGC中已有的知识，而且大多数模型只能预测单个标记的实体，因此这些模型还不能实际用于KGC。

3.预备知识

知识图谱是由实体和关系组成的网络。它可以被定义为:\(KG=\lbrace \mathcal{E},\mathcal{R},\mathcal{T}\rbrace\)，其中\(\mathcal{E}\)是实体的集合，\(\mathcal{R}\)是关系的集合。\(\mathcal{T}={(h,r,t)}⊆\mathcal{E}×\mathcal{R}×\mathcal{E}\)是三元组的集合，其中h和t是头尾实体，r是它们之间的关系。

3.1 知识图谱补全(KGC)

KGC任务旨在补全知识图中缺失的三元组\((h,r,t)∉\mathcal{T}\)。有两种主要的方法来完成这个任务，即链接预测和三元组分类，前者主要预测三重查询\((h,r,?)\)或\((?,r,t)\)，后者的目的是确定给定的三元\((h,r,t)\)是否正确。

3.2 封闭世界假设(CWA)

CWA认为没有出现在给定知识图谱中的三元组是错误的。这意味着，如果数据集由训练/验证/测试集组成，并且模型在测试集上进行测试，那么只有在整个数据集中出现的三元组才被认为是正确的。在CWA下，我们可以很容易地对模型的性能进行评估，而CWA本质上是一种近似，不能保证评估结果的准确性。

3.3 开放世界假设(OWA)

OWA认为知识图谱中包含的三元组是不完整的。因此，在开放世界假设下的评估更准确，更接近真实场景，但需要额外的人工注释来仔细验证知识图中不包含的完成的三元组是否正确。

封闭世界假设(CWA): 在封闭世界中若不知道某命题是否为真，则认定此命题为假，即不是已知的事物都为假

开放世界假设(OWA): 在开放世界中当前没有陈述的事情是未知的假定，即知识的缺乏不蕴涵虚假。

例子1：

提问:Mary是加拿大公民吗?

封闭世界回答:否。

开放世界回答:不知道(Mary可能有双重国籍)。

例子2：

陈述:Jane的母亲是Mary。

新陈述:Jane的母亲是Elizabeth。

封闭世界反应:错误。人只能有一个母亲。

开放世界反应:新事实。Mary就是Elizabeth。

4.模型方法

4.1 框架

本文提出了一种新的基于PLM的KGC模型PKGC，该模型利用PLM中的隐性知识和KGs中的结构化知识来推断新知识。具体来说，一方面，我们将一个三元组转换为提示句，以便在PLM中使用这些知识。如图2所示，给定一个三元组，我们的模型将其转换为三元组提示\(P^T\)和支持提示\(P^S\)，这两个提示被联合输入到预先训练的语言模型中。形式上，最终输入到PLM的文本T可以定义为：\(T=[CLS]P^T P^S[SEP]\)，语言模型中\([CLS]\)的输出用来预测给定三元组的标签。另一方面，我们将正类/负类三元组输入到我们的模型中进行三元组分类，并使用交叉熵损失进行训练。这样，我们的模型就可以利用KGs中的结构化信息。

在接下来的章节中，我们将在4.2节详细介绍三元组提示的设计策略，并在4.3节详细介绍支持提示的制作方法。此外，我们还将在4.4节解释我们的模型训练方法。

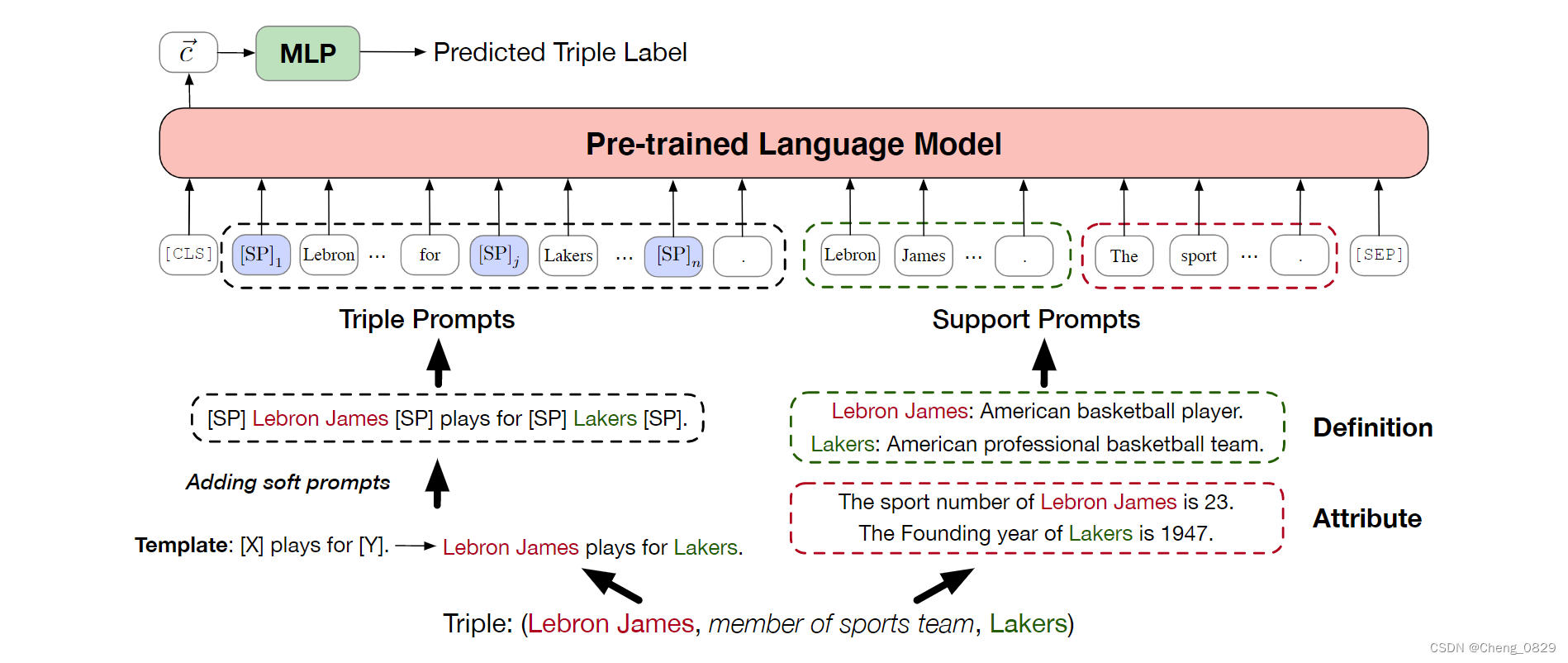
图2:用于三元组分类的PKGC模型说明。三元组被转换为三元提示符(左部分)和支持提示符(右部分)，以使用PLM进行分类。

4.2 三元组提示

为了更好地利用PLM中的隐性知识，我们将每个三元组转换为三元组提示。受LAMA的启发，对于每个关系r∈R，我们手动为关系设计一个固定模板，以表示相关三元组的语义。例如，在图2中，运动队关系成员的固定模板是"[X] plays for [Y]."。通过将[X]和[Y]替换为头部和尾部实体的标签，可以得到初步的三元组提示\(P^T_p\)。在图2中，\(P^T_p\)是"Lebron James plays for Lakers."。

为了使三元组提示更具表现力，我们还在\(P^T_p\)中添加了一些软提示，形成最终的三元组提示\(P^T\)。形式上，我们有一个用于软提示的向量查找表\(\mathbf{P} \in \mathbb{R}^{|R|×n×d}\)，其中n是一个三元组提示中包含的软提示符的总数，d是语言模型对应的词向量的维数。如图3所示，模板和实体标签将三元组提示分为6个位置，我们可以分别在其中插入软提示。每个位置的软提示数量分别为n1,n2,···n6，并且满足\(n=\sum^6_{i=1}n_i\)。对于三元组提示中的第k个软提示[SP]\(_\mathbf{k}\)，在输入语言模型时，将其对应的词向量替换为\(\mathbf{P}\)中关系r对应的第k个向量。随着训练的进行，向量查找表\(\mathbf{P}\)将不断更新，以便能更好地表示对应三元组的语义和固定模板。

软提示(Soft Prompt)： Soft Prompt是在向量空间优化出来的提示，从一个Hard Prompt开始初始化，通过梯度搜索等方式进行优化(不改变原始的提示向量的数量和位置)；
而Hard Prompt是人可以读的提示，即一段人类可以直观阅读的单词序列。

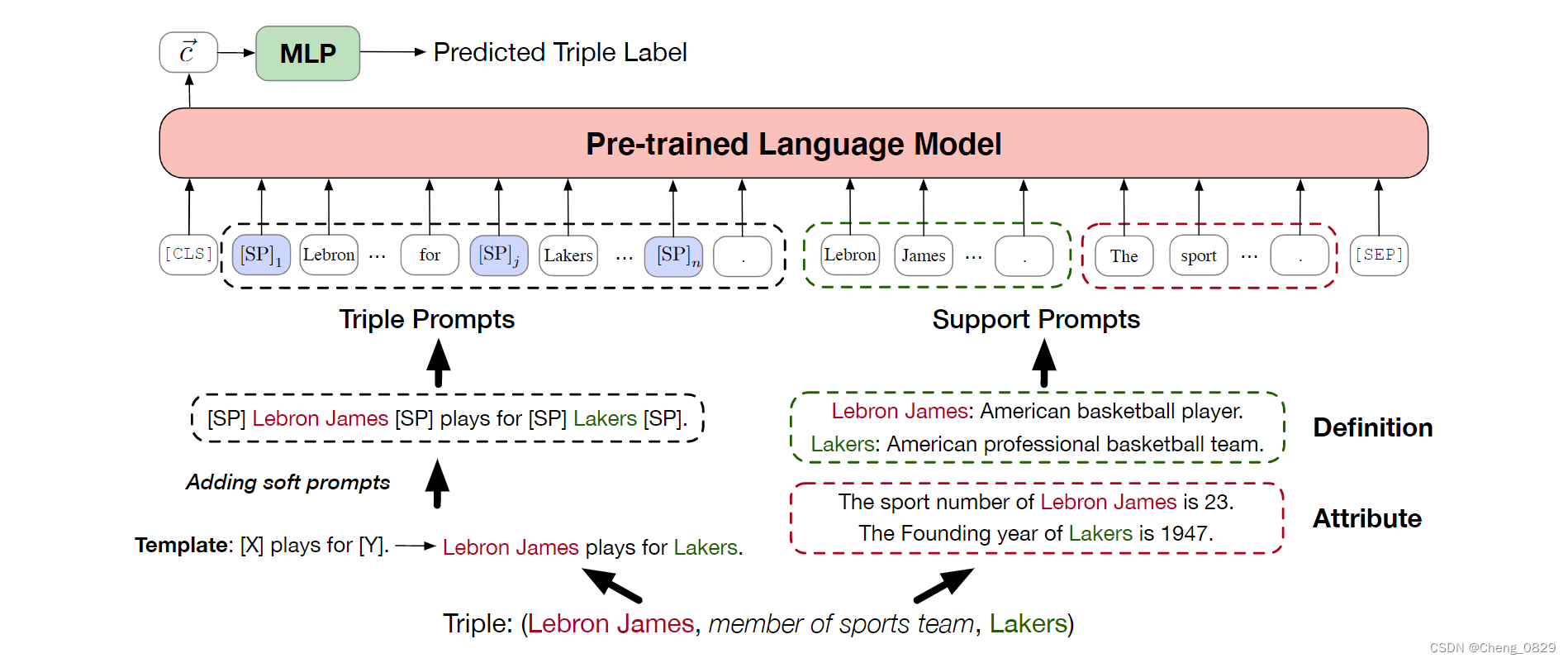
图3：将软提示插入三元组提示的图示。句子中的"Template"代表固定模板中的单词。我们最多可以在六个位置(下划线处)插入多个软提示，这些软提示的数量之和为n。

4.3 支持提示

KG中除了它本身的三元组信息外，还有许多可以帮助KGC的支持信息，如定义、属性等。在之前的KGE模型中，通常需要改变模型结构来引入特定类型的附加信息，这会带来大量额外的开销，不利于统一多类型支持信息。

由于语言的通用性，在不改变模型结构的情况下，很容易在模型中引入各种支持信息。如表1所示，我们定义模板把支持信息转换为相应的句子。对于一个三元组(h,r,t)，可能有多个对应的属性。为了避免过于复杂的模型，在本研究中，我们使用了随机策略来选择属性，即为一个三元组中的每个实体随机选择一个属性。

值得注意的是，我们的模型不需要呈现所有支持信息。如果不存在，就不添加相应的信息。此外，我们的模型还可以很好地支持更多其他类型的支持信息，只需手动定义表1中所示的相应模板即可。

表1：支持信息的模板。其中[Entity]、[Attribute]和[Value]分别表示实体、属性和值的标签。[定义文本]是实体定义对应的文本。

4.4 训练

我们的模型在三元组集合\(\mathcal{D}= \mathcal{T}∪\mathcal{T}^−\)上训练,用作三元组分类。具体来说，\(\mathcal{T}^-\)由两种类型的负类三元组组成:

1. 随机负类选择\(\mathcal{T}^−_{RAN}\)，通过将\(\mathcal{T}\)中三元组的头或尾实体随机替换为\(\mathcal{E}\)中的另一个实体而生成负类三元组。随机负类选择很简单，但也可以覆盖大多数实体。
2. 基于KGE的选择\(\mathcal{T}^−_{KGE}\)，把三元组的头或尾实体替换为KGE模型输出概率高的另一个实体。KGE负类选择相比于随机负类选择更麻烦。

在我们的模型中，存在一个超参数α来控制\(\mathcal{T}^−_{RAN}\)和\(\mathcal{T}^−_{KGE}\)的比值，即\(\frac{\left|\mathcal{T}_{\mathrm{RAN}}^{-}\right|}{\left|\mathcal{T}_{\mathrm{KGE}}^{-}\right|}=\frac{α}{1-α}\)。此外，我们还有一个超参数K来控制正、负三元组的比例，即\(|\mathcal{T}| = K·|\mathcal{T}^−|\)。给定三元组\(τ=(h,r,t)\)，三元组的分类预测概率可以定义为:

\[\mathbf{s}_\tau=\operatorname{Softmax}(\mathbf{Wc}) \]

其中,\(\mathbf{c}∈\mathbb{R}^d\)是输入标记[CLS]的输出向量，\(\mathbf{W}∈\mathbb{R}^{2×d}\)是一个线性神经网络。我们为优化器定义了以下交叉熵损失函数:

\[\mathcal{L}=-\sum_{\tau \in \mathcal{T} \cup \mathcal{T}^{-}}\left(y_\tau \log \left(\mathbf{s}_\tau^1\right)+\left(1-y_\tau\right) \frac{\log \left(\mathbf{s}_\tau^0\right)}{K}\right)\tag{2} \]

其中\(y_τ\)∈{0,1}是三元组\(τ\)的标签，\(s^0_τ\)，\(s^1_τ\)∈[0,1]是\(s_τ\)的前两个维度的值。