python 机器学习第二章(感知器学习算法)
第二章介绍单层神经元中的两类算法:感知器学习算法,自适应线性神经元学习算法
这一节主要讲感知器学习算法原理以及对应的python代码。
感知器学习算法的原理如下:
我们的大脑中的神经元是大脑中相互连接的神经元细胞,它可以处理和传递化学和电信号,那我们可以得到启示,我们可以认为神经细胞为一个具备二进制输出的逻辑门,树突会接收多个输入信号,如果累加的信号超过某一个阈值,经过细胞体的整合就会生成一个输出信号,并通过轴突进行传递。根据此原理,Frank Rossenblatt提出了第一个感知器学习法则。感知器算法可以自动通过优化权重系数,此系数与输入值的乘积决定了神经元是否被激活。
简单的示例图片总结:

感知器规则总结来说有如下几步:
1,将权重初始化为零或者一个极小的随机数
2,迭代所有训练样本X(i),执行如下操作:
(1) 计算输出值y
(2) 跟新权重。
感知器算法的优缺点:
优点:简单易用
缺点:对于无法完美线性可分的数据集,感知器算法将永远无法收敛(原因:在每次迭代过程中,总是存在至少一个分类错误的样本,从而导致权重的持续更新,导致无法收敛)
感知器算法Python代码如下:
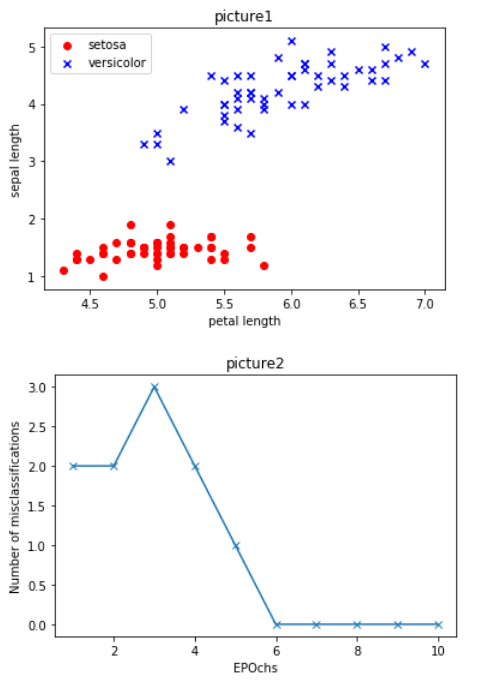
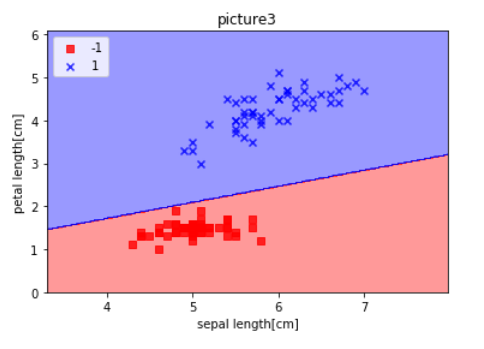
# 感知器模型 from matplotlib.colors import ListedColormap import numpy as np import pandas as pd import matplotlib.pyplot as plt df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data',header=None) df.tail() class Perceptron(object): def __init__(self,eta=0.01,n_iter=10): self.eta = eta self.n_iter = n_iter #实例化一个Perceptron 对象,并且给出一个学习速率eta,和一个迭代次数n_iter
def fit(self,X,y): self.w_ = np.zeros(1 + X.shape[1])#将self.w_中的权值初始化为一个零向量Rm+1 self.errors_ = [] for _ in range(self.n_iter): errors = 0 for xi,target in zip(X,y): update = self.eta*(target - self.predict(xi)) self.w_[1:] += update * xi self.w_[0] += update errors += int(update != 0.0) self.errors_.append(errors)#收集每轮迭代中的错误分类样本数量,并将其存放在self.errors_中 return self def net_input(self, X): return np.dot(X,self.w_[1:]) + self.w_[0]#np.dot()方法用于计算向量的点积wTx def predict(self, X): return np.where(self.net_input(X) >= 0.0, 1, -1)#在模型训练的时候此方法用来计算类标,也就是对数据打标签,在模型训练后,用于预测未知数据 def plot_decision_regions(X,y,classifier,resolution=0.02): markers =('s','x','o','^','v') colors =('red','blue','lightgreen','gray','cyan') cmap = ListedColormap(colors[:len(np.unique(y))]) x1_min, x1_max = X[:,0].min()-1, X[:,0].max()+1 x2_min, x2_max = X[:,1].min()-1, X[:,1].max()+1 xx1,xx2 = np.meshgrid(np.arange(x1_min,x1_max,resolution),np.arange(x2_min,x2_max,resolution)) Z= classifier.predict(np.array([xx1.ravel(),xx2.ravel()]).T) Z = Z.reshape(xx1.shape) plt.contourf(xx1,xx2,Z,alpha=0.4,cmap=cmap) plt.xlim(xx1.min(),xx1.max()) plt.ylim(xx2.min(),xx2.max()) for idx,cl in enumerate(np.unique(y)): plt.scatter(x=X[y == cl,0],y=X[y == cl,1],alpha=0.8,c=cmap(idx),marker=markers[idx],label=cl) y=df.iloc[0:100,4].values y=np.where(y == 'Iris-setosa',-1,1) X=df.iloc[0:100, [0,2]].values plt.scatter(X[0:50,0],X[0:50,1],color='red',marker='o',label='setosa') plt.scatter(X[50:100,0],X[50:100,1],color='blue',marker='x',label='versicolor') plt.xlabel('petal length') plt.ylabel('sepal length') plt.legend(loc='upper left') plt.title('picture1') plt.show() # 图一 ppn = Perceptron(eta=0.1,n_iter=10) ppn.fit(X,y) plt.plot(range(1,len(ppn.errors_)+1),ppn.errors_,marker='x') plt.title('picture2') plt.xlabel('EPOchs') plt.ylabel('Number of misclassifications') plt.show() # 图二 plot_decision_regions(X,y,classifier = ppn) plt.xlabel('sepal length[cm]') plt.ylabel('petal length[cm]') plt.legend(loc='upper left') plt.title('picture3') plt.show() # 图三




【推荐】还在用 ECharts 开发大屏?试试这款永久免费的开源 BI 工具!
【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步