PMI(Pointwise Mutual Information)
公式
几句废话
先来一两句废话,要想解释好点互信息必须学会科学上网,当然如果没有条件本篇博客会具体介绍。上网百度得到的搜索结果如下图1-1所示,事实证明百度不够自信,这么重要的概念百度学术里面没有?淦!居然都是来自CSDN,然而CSDN有个致命的缺点,就是对于某个问题的讲解原创比较少,后面的人基本就是copy了。当然CSDN大牛依旧非常多,向原创致敬,向大佬看齐!接着跑去了维基百科搜索了一番,结果如图1-2所示。没有对比就没有伤害,不是为了黑而黑,实事求是的讲百度在相关学术方面做的真的不咋地。好啦下面吧维基百科的内容拿过来学习!咱们一段一段来分析(重回阅读理解哈哈):


图 1-1 图 1-2
以下内容来自维基百科:

解读
其实能看懂英文也就不用看这段文字了,不过嫌麻烦的话本段文字应该能让你基本读懂!若本人误解某些概念还望各位批评指正!下面开始!
点间互信息(来自维基百科,免费的百科全书)
点间互信息或者点互信息是一种用于信息论和统计学中的关联性度量,与点互信息PMI中的互信息MI恰好相反,点互信息PMI是关于单个事件,而互信息MI是关于所有可能事件的平均值。这里解释一下,互信息请参考https://blog.csdn.net/cj151525/article/details/112546901,我们知道互信息的公式为:
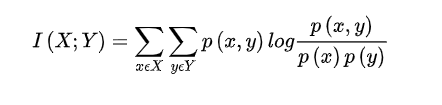 那么我们发现点互信息就是后面这个log,所以PMI是关于单个事件的,而MI是所有点互信息乘以期望
那么我们发现点互信息就是后面这个log,所以PMI是关于单个事件的,而MI是所有点互信息乘以期望累加起来,也就是所有点的点互信息的均值嘛!有点连点成线的感觉。这也就是为什么叫做点互信息的原因吧,妙啊!好啦,接下来继续说:
定义
一对离散随机变量 x 和 y 的结果 x 和 y 的 PMI 量化了给定它们联合分布的概率和假设独立的个体分布之间的差异。数学上:
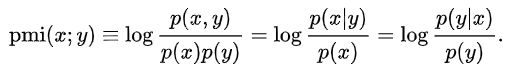
随机变量 x 和 y 的互信息(MI)是 PMI 的期望值(包括所有可能的结果)。点互信息结果是对称的(),它可以取正值或者负值,但是如果X和Y相对独立它就等于0(解释:X与Y独立则
,带入上面公式结果为0 )。注意即使PMI可能是负值或者正值,它的所有事件的期望结果互信息MI是正值。当X和Y完全相关时(
或者
),PMI最大化,因为log函数单调增,概率最大值为1,。界限如下所示:
![]()
最后,如果不变,但是
变小,则
将变大。
下面举个栗子说明:(可以理解两个不均匀的硬币A、B各抛掷一次,x=0表示A正面,x=1表示A反面,y=0表示B正面,y=1表示B反面,各抛掷一次得到)
| x | y | p(x, y) |
|---|---|---|
| 0 | 0 | 0.1 |
| 0 | 1 | 0.7 |
| 1 | 0 | 0.15 |
| 1 | 1 | 0.05 |
使用这个表格我们可以边缘化以获得下面附加的表格:
| p(x) | p(y) | |
|---|---|---|
| 0 | 0.8 | 0.25 |
| 1 | 0.2 | 0.75 |
我们可以计算得到以下四个值:
| pmi(x=0;y=0) | = | −1 |
| pmi(x=0;y=1) | = | 0.222392 |
| pmi(x=1;y=0) | = | 1.584963 |
| pmi(x=1;y=1) | = | -1.584963 |
点间互信息有许多与互信息相同的关系,特别是,

是自信息,公式为
Normalized pointwise mutual information (npmi)
标准点互信息
点互信息可以被标准化到区间[-1,1]之内,极限值-1表示从未同时出现,0表示独立,1表示完全同时发生。
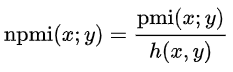
这儿 是联合自信息,公式为

应用
在20世纪90年代计算语言学,PMI 已经被用于寻找词汇之间的搭配和联系。例如,文本语料库中出现和同时出现的词的计数可以用来分别近似概率p (x)和p (x,y)。下表显示了在维基百科(Wikipedia,2015年10月转储)的前5000万个单词中获得最多和最少 PMI 得分的单词对计数,过滤了1000个或更多同时出现的单词。每次计数的频率可以用50,000,952除以。(注意: 本例中使用自然对数基数e来计算 PMI 值,而不是使用对数基数2。
好的搭配对具有较高的 PMI,因为共现概率仅略低于每个词的共现概率。相反,一对出现概率大大高于同出现概率的单词得到一个较小的 PMI 分值。所以说PMI越大说明两个词共现的频率更大,相关性越大,反之PMI越小两个词共现的概率越低。
总之,PMI越大越相关,越小越无关。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号