SCP(Symmetrical Conditional Probability)
对称条件概率
这个概念百度和谷歌都查了,单独的解释寥寥无几,在知网查也没找到可能是我方法不对,知道的朋友可以告诉我一下,谢谢!最后在一篇韩国人的论文中找到了一些解释,欧巴给力思密达!如下图:

其实我们高中就知道条件概率:
,我们知道条件概率是不对称的
, 这两个条件概率不相等,既然如此那何来对称?见下面论文解释:

大概意思就是解释了和他论文相关的一些东西,然后最后一句话就是说“对称条件概率为(3)”,我们只需要知道最后一句,因为这里他也没有详细解释对称条件概率,因此得到的对称条件概率公式为:
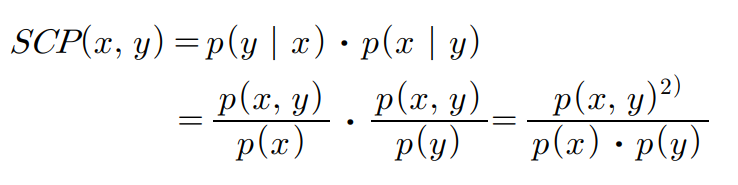
一看这个公式感觉耍流氓,SCP(x,y) 肯定等于SCP(y,x)呀,这能不等于嘛,肯定相等!然而这个概念的实际意义在哪里呢?从这篇论文我们得不到答案,再找了一篇发现了有引用SCP的脚注:

至此,终于找到了SCP出处了,顿时也明白了为什么百度谷歌很难找到一些概念,因为这些新提出的概念可能不是什么非常惊人的定理或者真理,只是用来解决某个方法的某个问题,因此不研究该行业的人员可能就不太了解,而行业人员经常遇见就自然而然懂得,所以本文只是记录一些自己学习的历程和可能帮助有需要的朋友:

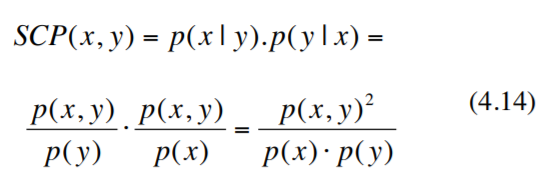
翻译过来就是:让我们考虑字母x,y。我们提出一个新的测量x和y之间的“相关性”的度量方法是:取两者给定的条件概率,然后将两者相乘。让我们把它叫做SCP(对称条件概率)。
通过几篇论文我们都知道SCP总是和n-grams算法一起出现。到这里我们终于知道 SCP就是用来测量两个事件的相关性,那这个值大表示相关性强还是弱呢?我们不妨思考一下:假设x=“明天会出大太阳”,y=“明天天晴”,再假设天晴一定会出太阳,出太阳一定天晴。则 p(x|y)=1 , p(y|x)=1 ,SCP(x,y)=1*1=1,可知SCP=1时,x与y的相关性极强。若假设z=“明天下暴雨”,则 p(x|z)=0 , p(z|x)=0 ,SCP(x,z)=0。也就是说两件对立事件的SCP为0,即SCP=0时,x与z没有相关性。因此得出猜想:SCP越大,两个事件相关性越强,SCP越小相关性越弱!
为什么说猜想而不是结论,因为只是举特例说明问题不具有普遍性,没有从数学角度进行分析证明,到这里也差不多了解了这个概念,证明的话可以自己尝试一下,有证出的朋友分享一下!

