邻接熵(Branch Entropy)
邻接熵论文:Huang J H, Powers D. Chinese Word Segmentation Based on Contextual Entropy[C].
Proceedings of the 17th Asian Pacific Conference on Language Information and Computation,
2003:152-158
本篇博客邻接熵概念引自:王欣. 一种基于多字互信息与邻接熵的改进新词合成算法[J]. 现代计算机:专业版, 2018. 侵删!
两个汉字是否能够构成一个词语,除了推断汉字之间的结合程度外,词语相邻 字的多样性也是一个衡量标准。边界自由度是指与一个字符串相邻的所有字符种 类的数量[43]。边界自由度越大,表示字符串的相邻字符集合中的字符类别就越多, 与该字符串相邻的字符就越丰富多样,那么该字符串的边界就越明确,这个字符串 成为词语的可能性就越大。目前常用的外部统计量包括邻接熵[46]和邻接类别[47] (Accessor Variety, AV)。通过已有的对比方法发现邻接熵比邻接类别的准确率要 高,所以大多数研究都是以邻接熵作为衡量字符串成词概率的外部统计量。 信息熵是信息论中的概念,表示一个随机变量的不确定性的均值。变量的熵越 大,那么这个变量的不确定性就越大,它携带的信息量就越丰富,同时正确估计该 变量的值的可能性也越大[44]。假设𝑋是一个离散型随机变量,其取值范围为R,当 𝑥(𝑥𝜖𝑅)时,它的概率分布为p(𝑥) = 𝑃(𝑋 = 𝑥)。那么,随机变量的信息熵的计算公 式如式 2.3 所示。
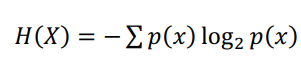 ................................(式 2.3)
................................(式 2.3)
约定,0 log 0 = 0。 在新词发现任务中,确定词语的左边界和右边界的统计量通常是左邻接熵和 右邻接熵 [48,49]。一个候选词组的左邻接熵是指该候选词组和与它左边所有相邻的 字结合的信息熵之和,用来判断该候选词组的左邻接字的多样性。左邻接熵越大, 说明该候选词组左边相邻的字的种类越多,那么该候选词组成为某个词语的左边 界的可能性越大;反之,左邻接熵越小,该候选词组左边相邻的字的种类越少,它 不是某个词语的左边界的情况就越肯定,那么就应该对该候选词组向左扩展直到 左边界确定为止。式 2.4 为候选词的左邻接熵计算公式。
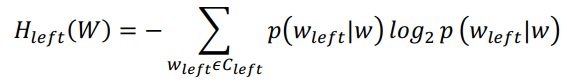 .........................................................(式 2.4)
.........................................................(式 2.4)
其中, 𝐻𝑙𝑒𝑓𝑡(𝑊)是候选词语𝑤的左邻接熵, 𝐶𝑙𝑒𝑓𝑡是候选词𝑤的左邻接字集合,𝑝(𝑤𝑙𝑒𝑓𝑡|𝑤)是候选词𝑤出现的情况下它左边的邻接字是𝑤𝑙𝑒𝑓𝑡的条件概率。 如果𝑁(𝑤𝑙𝑒𝑓𝑡)是左邻接字𝑤𝑙𝑒𝑓𝑡和候选词𝑤共同出现的频率, 𝑁(𝑤)是候选词𝑤单独出现的频率, 𝑝(𝑤𝑙𝑒𝑓𝑡|𝑤)的计算公式如式 2.5 所示。
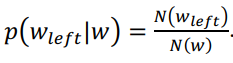 ......................................(式 2.5)
......................................(式 2.5)
同理, 右邻接熵用来推断词语的右边界,候选词的右邻接熵计算公式见式 2.6。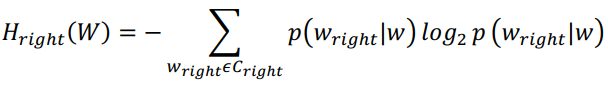 ........................................................(式 2.6)
........................................................(式 2.6)
其中,𝐻𝑟𝑖𝑔ℎ𝑡(𝑊)是候选词𝑤的右邻接熵, 𝐶𝑟𝑖𝑔ℎ𝑡是候选词的𝑤的右邻接字集合,𝑝(𝑤𝑟𝑖𝑔ℎ𝑡|𝑤)是候选的词𝑤出现的情况下其右邻接字是𝑤𝑟𝑖𝑔ℎ𝑡的条件概率。 如果𝑁(𝑤𝑟𝑖𝑔ℎ𝑡)是𝑤𝑟𝑖𝑔ℎ𝑡 和𝑤 同时出现的概率, 𝑁(𝑤)是𝑤 单独出现的概率,那么𝑝(𝑤𝑟𝑖𝑔ℎ𝑡|𝑤)的计算公式见式 2.7。
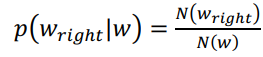 ....................................(式 2.7)
....................................(式 2.7)
因此,如果𝐻𝑙𝑒𝑓𝑡(𝑊)大于指定的阈值,则左边界确定;如果𝐻𝑟𝑖𝑔ℎ𝑡(𝑊)大于制定的阈值,则右边界确定。
当前确定新词左右边界的方法一般有两种,邻接熵(Branch Entropy,BE)和邻接变化数(Accessor Variety,AV),本文采用左右邻接熵来确定新词的左右边界。邻接熵[15]可以衡量候选新词的左右邻接字符的不确定性,其不确定性越大,说明其邻接字符包含的信息越多,其成词的概率就越高。
左邻接熵:
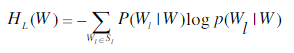
右邻接熵:
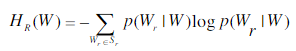
其中:是候选词
的左邻接字的集合,
是候选词W的右邻接字的集合;
表示
是候选词W的左邻接字的条件概率,
表示
为候选词W的右邻接字的条件概率。其中
和
的计算公式为:
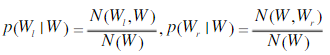
其中:表示
和
共同出现的次数,
表示W出现的次数。同理,
表示
和
共同出现的次数,W(N) 表示W出现的次数。

