Loading

极大似然估计直观理解

目录

 

一、公式

二、如何理解

三、参考

一、公式

1、离散型

2、连续型

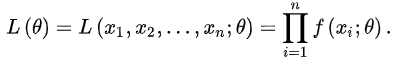
二、如何理解

直观意义：刻画参数\theta与数据的匹配程度。极大似然估计法原理就是固定样本观测值(x1,x2,...,xn)（x1,x2,...,xn），选择参数\theta,使 L(\theta ) 最大。通俗来说，就是已知观测值请你解释这个样本空间为什么会是这样子的。那怎么解释呢？使用极大似然估计就能解释。举个栗子：

暗箱中放有n个黑白小球，我们不知道黑球白球各为多少。那在不能打开的情况下如何估计黑球多少个呢？抽样！！！，我们随机有放回抽样n次，得到n1个黑球，n2个白球。当然我们立即可以得出比较科学的结论，黑球大概n1个，白球n2个。那理论支撑在哪？这是我们最为直观的结论，黑球的概率为 n1/n 。下面我们用极大似然来估计一下。

首先记黑球的概率为 \theta ，则白球概率为 1-\theta ，因为抽样结果是确定的，所以有我们理应可以找到  \theta 使得发生抽取的样本这件事的概率为1，即  L(\theta )=\theta ^{n1}(1-\theta )^{n2} 为 1，所以为什么是极大而不是极小似然估计！但是1是最大值，往往我们退而求次求极大值即可，即两边加上 ln 求导为0解出 \theta 即可，最后求到的   \theta = \frac{n1}{n} ,这就通过一种方法求到的结果就与我们的直觉一样了。

三、参考

https://blog.csdn.net/qq_38675397/

 

 

 

posted @ 2021-02-06 14:32  cheney-pro  阅读(502)  评论(0)  编辑  收藏  举报