吃西瓜—先磨刀之概率论

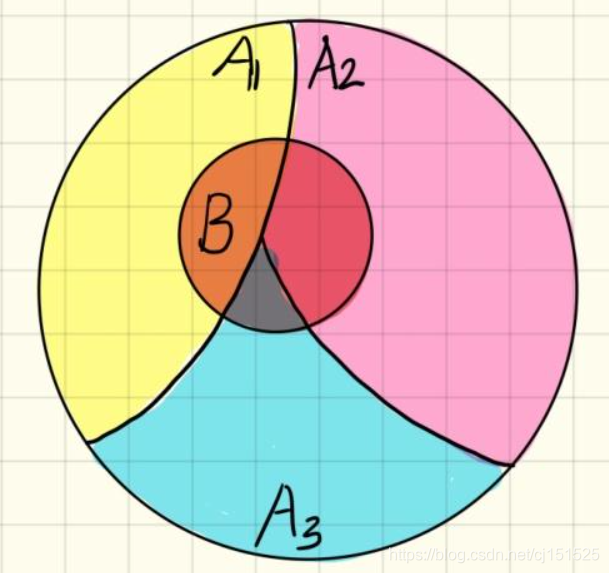
大圆为A事件，小圆为B事件，那么 P(B)=P(BA1)+P(BA2)+P(BA3); 所以有公式： $P(B)=\sum_{i=1}^{n}P(BA_{i})$ , 根据条件概率公式又知道 $P(BA_{i})=P(B|A_{i})P(A_{i})$ , 所以在已知 $P(B|A_{i}),P(A_{i})$ 的情况下，求P(B)，即为全概率公式： $P(B)=\sum_{i=1}^{n}P(B|A_{i})P(A_{i})$ 。用自己的语言描述就是：将B每一小块的概率加起来即为B的概率，而每一小块由条件概率求得！

贝叶斯公式

已知结果概率P(B)推原因概率,即第i个事件的条件概率 $P(A_{i}|B)$ ，也称为后验概率公式。 $P(A_{i}|B)=\frac{P(A_{i}B)}{P(B)}$ , 分子使用乘法公式得到 $P(A_{i}B)=P(B|A_{i})P(A_{i})$ ，分母使用全概率公式得到 $P(B)=\sum_{i=1}^{n}P(B|A_{i})P(A_{i})$ ，即 $P(A_{i}|B)=\frac{P(B|A_{i})P(A_{i})}{\sum_{j=1}^{n}P(B|A_{j})P(A_{j})}$ 。

三、随机变量

概率密度：描述连续型随机变量的取值的统计规律。

概率分布律：描述离散随机变量的取值的统计规律。

分布函数：连续型随机变量的区间概率，对概率密度求积分即可，即为概率密度的区间面积。F(x)=P(X<x) ;

四、数字特征

方差：度量随机变量和数学期望之间的偏离程度。 $D(X)=E[X-E(X)]^{2}$ ,刻画随机变量取值的分散程度！

标准差： $\sqrt{D(X)}$ , 为了保证与原数据单位具有相同的量纲，对方差开平方就是标准差。

协方差：前提X,Y不相互独立，为了衡量两个变量间的相关程度或者联系。 $Cov(X,Y)=E({[X-E(x)]*[Y-E(Y)] })$ ,其中 $Cov(X,X)=D(X),Cov(Y,Y)=D(Y)$ 。

协方差矩阵：随机变量两两求协方差，对角线为自己的方差。

相关系数：在相同量纲下，衡量随机变量X和Y之间的相关程度协方差有一定作用，但是不同量纲下，一般使用相关系数来衡量， $\rho _{xy}=\frac{Cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}$ , [0.8,1] 极强相关，[0.6,0.8]强相关，[0,0.2]极弱相关，若为负数，则有负相关，-1 完全负线性相关，0 不存在线性关系。注意相关系数只能判断是否有线性关系，非线性关系无法确定！！！

相关系数矩阵：随机变量直接两两求相关系数，对角线为自己与自己的相关系数为1 。注意，相关系数与协方差主要区别就是是否消除量纲！！！

五、参数（总体样本的均值、方差、拟合函数的参数等等）估计

参数估计包括点估计与区间估计，点估计通常是从总体样本中取样，然后用样本的统计量估计未知参数，例如使用样本的均值估计总体均值。点估计仅仅是未知参数的近似值，而近似值的误差范围没有明确给出，这就缺乏一定可信度，而区间估计正好弥补了这一缺点。

最小二乘法：真实值与预测值之差的平方之和。求出偏差最小平方和，例如使用 f(x)=a+bx 进行拟合, $Q=\sum_{i=1}^{n}(y_{i}-f(x_{i}))^{2}$ ,令偏导为0，解出函数参数a,b。

极大似然估计：寻找使事件发生概率最大的可能情况的参数估计方法。例如一个袋子有1000个黑、白球，请问黑球几何？我们随机取出100个，发现黑球72个，白球28个。现在我们知道了实验结果，需要估计参数黑球的个数及其白球的个数！什么情况下得到这个实验结果的参数能使得取得这个实验结果的概率最大？答案就是当袋子中黑球720个，白球280个的时候，得到这个实验结果的概率是最大的，所以得出了参数是，黑球720个，白球280个！

极大似然估计如何使用呢？分为离散型与连续型，其实都一样，核心思想就是假设参数为 $\theta$ ，然后将每一个样本概率累乘起来，离散： $L(\theta )=\prod_{i=1}^{n}p(x_{i};\theta )$ ,连续： $L(\theta )=\prod_{i=1}^{n}f(x_{i};\theta )$ 。然后在参数可能的范围之内寻找使得 $L(\theta )$ 最大的参数 $\theta$ 即可，两边取对数求导即可求得 $\theta$ 。

区间估计：由样本确定两个统计量 $\theta_{1} ,\theta_{2}$ ，满足 $P(\theta_{1}<\theta<\theta_{2})=1-\alpha$ ,则区间 $(\theta_{1} ,\theta_{2})$ 称之为 $\theta$ 的置信水平 $1-\alpha$ 的置信区间， $\theta_{1}$ 与 $\theta_{2}$ 分别是此置信区间的上下限。在多次等容量的抽取样本中，至少有 $100(1-\alpha )%$ 的区间包含 $\theta$ 。