【单调栈】

单调栈

采取的是空间换时间的方式。将历史信息保存在具有自己定义出入栈规则的栈中，来达到记忆的效果，实现了空间换时间。
自己定义的出入栈规则，从栈顶到栈底单调递增来举例:在这就是指栈内的顺序只能是自顶向底，依次递增才可以入栈。如果当前待入栈的元素大于栈顶，就需要把这个栈顶元素弹出，并循环比较下一个栈顶元素，直至栈顶元素大于当前待入栈元素才可以。

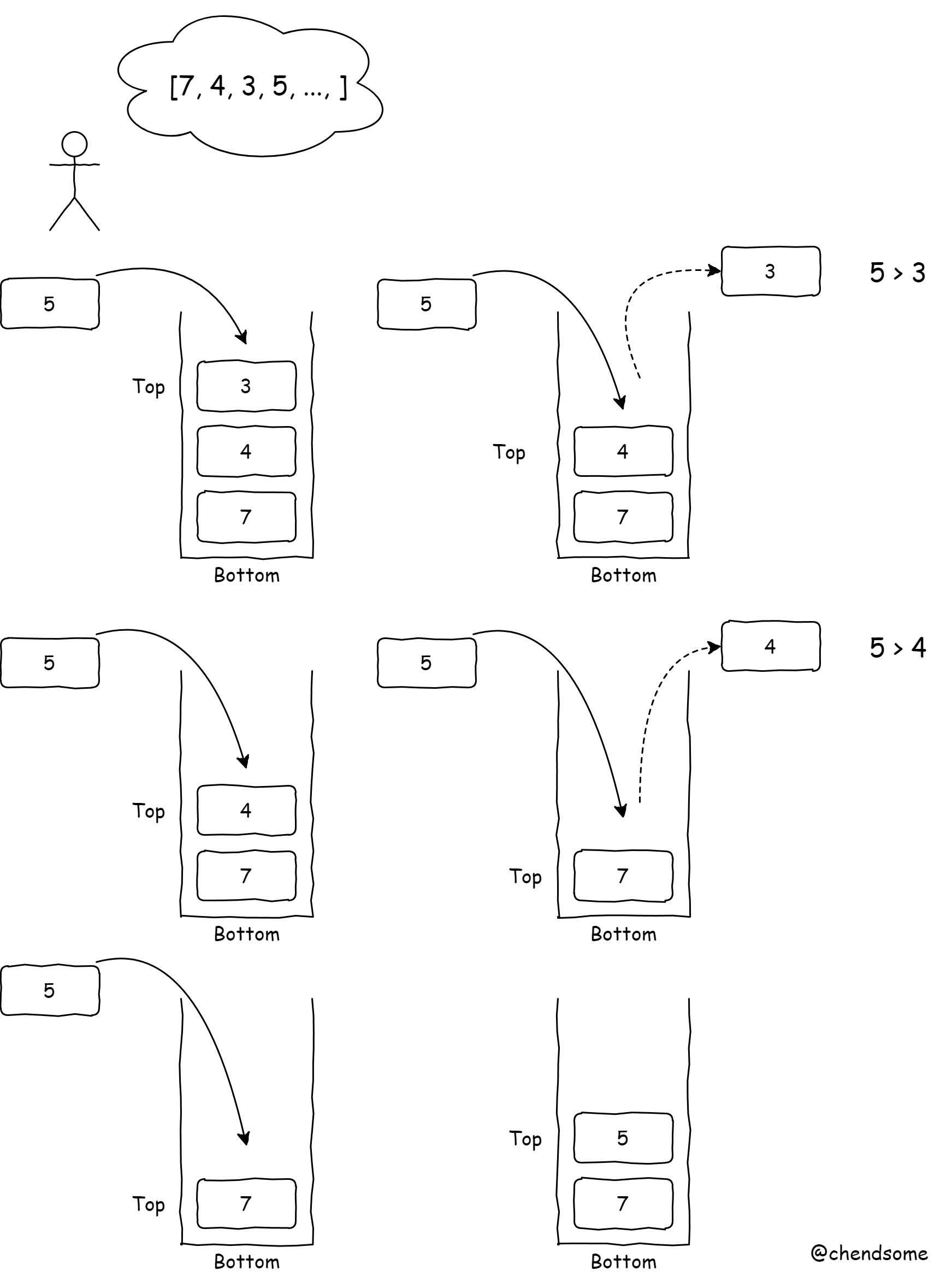
什么时候用单调栈呢？

选自代码随想录

通常是一维数组，要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置，此时我们就要想到可以用单调栈了

以leetcode的一道题为例

739. 每日温度

给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。

输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]

如果当前待入栈元素大于栈顶，说明当前元素就是第一个比栈顶大的元素，此时就需要把栈顶元素弹出，并比较下一个栈顶元素。

class Solution {
    public int[] dailyTemperatures(int[] temperatures) {

        int n = temperatures.length;
        int[] result = new int[n];

        Deque<Integer> stack = new LinkedList<>();
        stack.push(0);
        for (int i = 1; i < n; i++) {
            // 队列不为空，且 当前带入栈元素 大于 当前栈顶元素  执行 出栈， 并计算栈顶元素的任务
            while (!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]) {
                result[stack.peek()] = i - stack.pop();
            }
            // 队列空了，或者是已经比较完了，准备入栈了，入栈
            stack.push(i);
        }
        return result;
    }
}

84.柱状图中最大的矩形

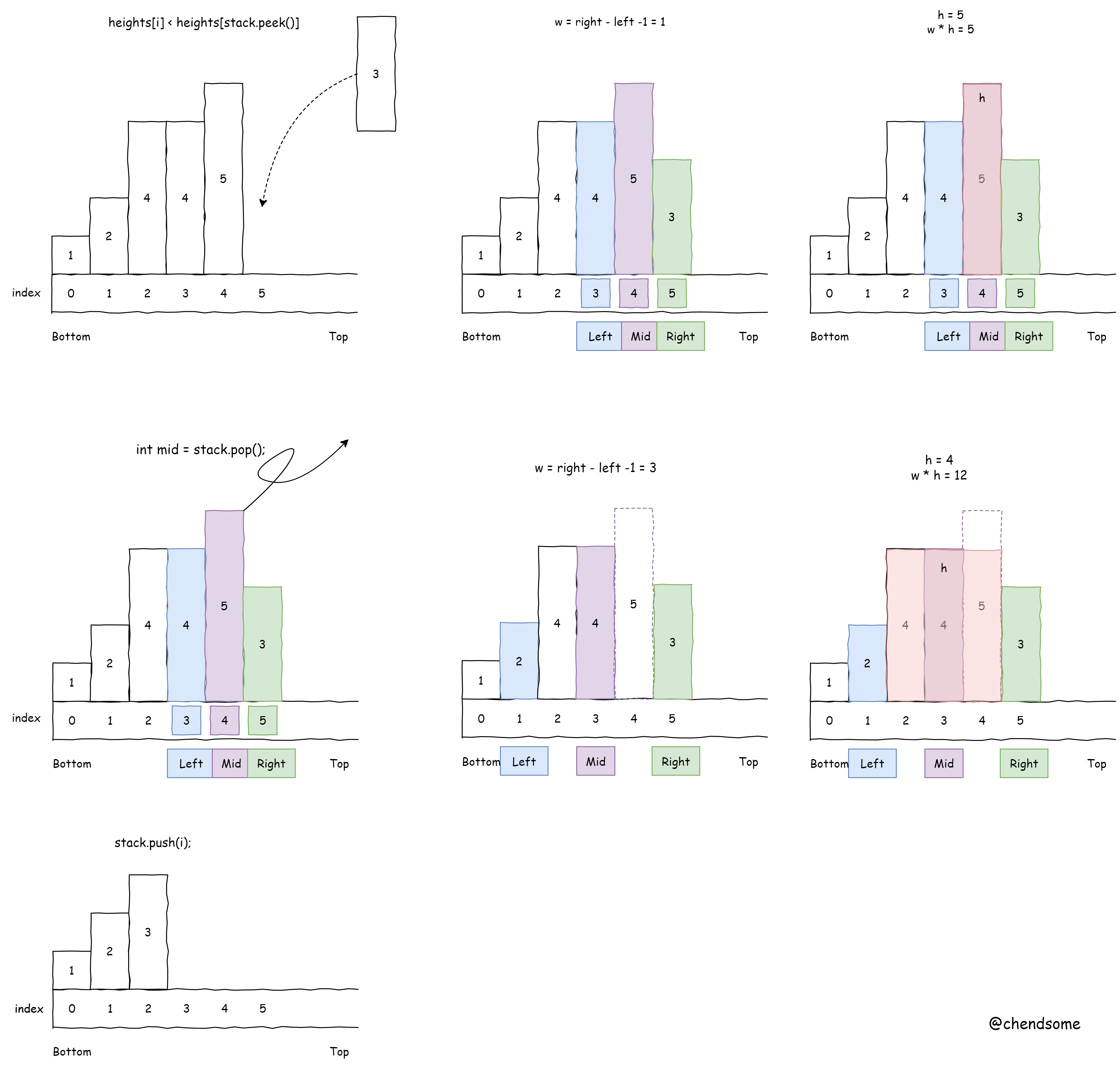
class Solution {
    public int largestRectangleArea(int[] heights) {
        int res = 0;
        Deque<Integer> stack = new LinkedList<>();

        // 数组扩容，在头和尾各加入一个元素
        int [] newHeights = new int[heights.length + 2];
        newHeights[0] = 0;
        newHeights[newHeights.length - 1] = 0;
        for (int index = 0; index < heights.length; index++){
            newHeights[index + 1] = heights[index];
        }

        heights = newHeights;

        stack.push(0);
        for (int i = 1; i < heights.length; i++){
            if(heights[i] > heights[stack.peek()]){
                stack.push(i);
            } else if( heights[i] == heights[stack.peek()]){
                stack.pop();
                stack.push(i);
            }else {
                while (!stack.isEmpty() && heights[i] < heights[stack.peek()]){
                    int mid = stack.pop();
                    if (!stack.isEmpty()){
                        int left = stack.peek();
                        int right = i;
                        int w = right - left - 1;
                        int h = heights[mid];
                        res = Math.max(res, w * h);
                    }
                }
                stack.push(i);
            }
        }
        return res;


    }
}